基于改进重复控制和模糊PI自整定的并网逆变器设计

宋新甫，于国康，孟高军，王耿耿

（1.国网新疆电力有限公司 经济技术研究院，新疆 乌鲁木齐 830011； 2.南京工程学院 电力工程学院，江苏南京 211100）

0 引言

可再生能源接入的配电网容量小，负荷种类多，电网内存在电压、电流谐波、无功功率不平衡以及电压波动跌落等电能质量问题，特别在公共连接点（Point of Common Coupling，PCC）处的电能质量问题更加突出[1]，[2]。

为解决上述问题，有学者提出多功能并网逆变器的概念。 文献[3]，[4]介绍了在实际配电网中，光伏并网逆变器引入无功补偿功能，能够为工程应用带来巨大的经济价值。 文献[5]，[6]针对多功能并网逆变器的无功问题，提出一种G-H 下垂控制策略，利用电网内并网逆变器数量较多且互联的特点，将电网内的无功电流在各逆变器间平均分配，从而有效改善电网的无功问题。

重复控制器是根据内模原理得到的控制策略[7]。 文献[8]提出一种基于重复控制与PI 控制的复合控制方法，然而，这种组合控制下系统的稳态精度和动态性能受PI 参数的影响较大，且复合控制的结构也相对复杂。 文献[9]，[10]采用平推法结合重复预测控制来改善动态特性，但平推法属于差一拍控制，下一拍的预测值采用的是检测指令值，无法做到精确跟踪参考电流。 文献[11]针对重复控制延迟时间较长的缺点，提出了将重复控制应用于1/6 基波周期下，有效提高了控制器的响应速度，但坐标变换和解耦过程较为复杂，而且重复控制对周期性输入无差跟随这一特点未得到充分发挥。 综上所述，现有文献往往很难同时兼顾系统稳定误差和动态性能的要求。

本文以具有无功补偿的多功能并网逆变器为研究对象，提出一种改进重复控制与模糊PI 自整定控制并联的控制策略。 首先，采用基于SSIF 的电流检测方法，补偿本地负荷所需的无功功率。同时，运用基于改进型重复控制算法的零稳态误差能力，保证系统的稳态精度；引入模糊控制技术，根据误差大小在线调整PI 参数，降低系统的动态响应时间。 最后，通过仿真和实验，验证了所设计的内环控制器能够满足要求。

1 多功能并网逆变器结构与控制分析

1.1 逆变器主电路图

如图1 所示：T1～T6为三相全控型半桥电路的IGBT 功率开关管，每个开关管反并联一个二极管；由每相桥臂的中点引出3 个相线，经过滤波电路接入三相电网，其中L1，L2分别为逆变器侧电感、电网侧电感，与滤波电容C 构成LCL 滤波电路；逆变器与本地负荷接到PCC，通过升压变压器接入电网；Ugrid为交流侧相电压有效值。

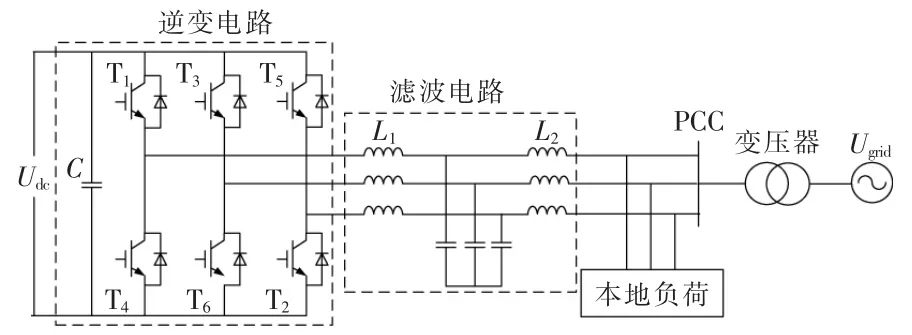
图1 多功能并网逆变器主电路图Fig.1 Main circuit diagram of multi-functional grid-connected inverter

1.2 多功能并网逆变器控制策略

在图1 所示主电路拓扑的基础上，为增强LCL 型并网逆变器的稳定性，本文采取在LCL 滤波器回路中加入电阻器增强系统阻尼，将滤波电容C 分成C1，C2，同时检测本地负载电流无功分量以及生成内环参考电流，其控制策略如图2 所示。

图2 多动能并网逆变器控制策略Fig.2 Control strategy of multi-functional grid-connected inverter

图2 中，逆变器的输出电流iabc由两部分组成，一部分为负载电流iLabc，由于本地负载的复杂性，iLabc中包含有大量无功分量； 另一部分为馈网电流igabc，只能包含基波正序有功分量。 为了补偿本地负荷所需的无功功率和提高电流控制精度，采用图2 所示的控制策略，将iLabc通过电流检测和变换后合成参考电流iLabcref，同时将iabc输入到内环控制器中，使其跟踪iLabcref变化。最后，内环控制器的输出电流 ioutput经过 PWM 环节作用，生成IGBT 驱动信号，最终控制并网逆变器电力输出，完成对本地无功负荷快速精确补偿。

2 电流检测和生成参考电流方法

电网中存在的谐波会对系统电流检测产生影响。 为提高电流检测精度，本文采用基于SSIF 的电流检测方法，实现对正序信号和负序信号同时运算的目的，其基本原理如图3 所示。

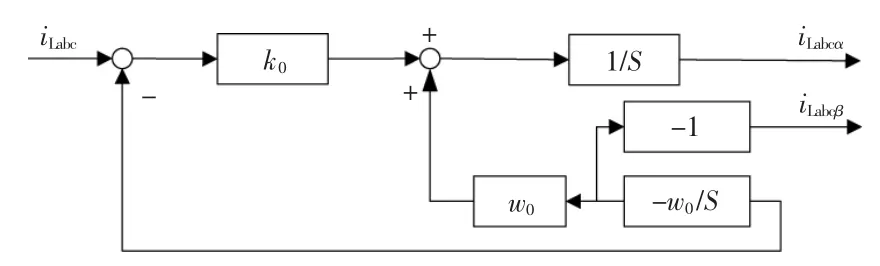
图3 SSIF 原理图Fig.3 Schematic diagram of SSIF

SSIF 的作用是将输入分解为基波分量和虚拟正交分量，当SSIF 的输入为负载电流时，SSIF的输出 iLabcα和 iLabcβ分别为负载电流基波分量和虚拟正交分量。 此时，根据瞬时无功理论，可以得到待补偿的本地无功功率。

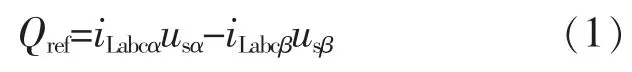
式中：usα，usβ分别为逆变器并网电压 us的基波分量、虚拟正交分量，其生成方式与 iLabcα，iLabcβ方式相同。

从而得到参考电流计算方法如下：

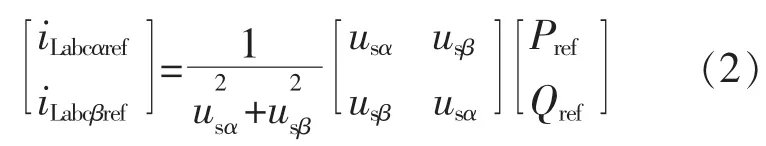
式中：Pref为逆变器输出有功功率参考值，可由上层控制系统指定；iLabcαref为参考电流的基波分量。

综上所述，基于SSIF 的参考电流合成原理图如图4 所示。

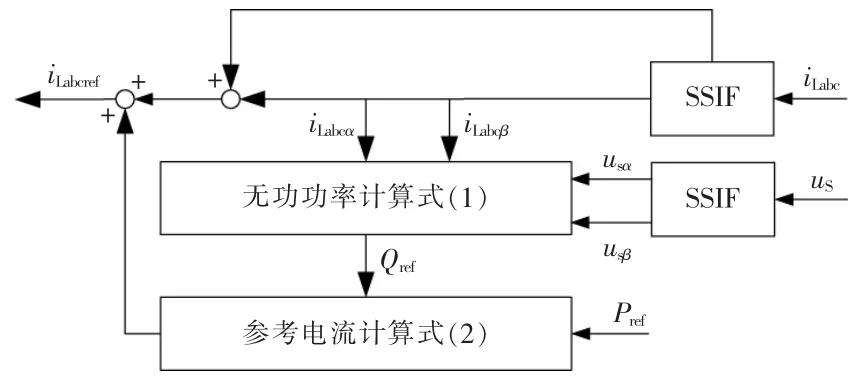
图4 基于SSIF 的参考电流合成原理图Fig.4 Schematic diagram of reference current synthesis based on SSIF

3 内环控制器设计

3.1 被控对象分析

根据图2 所示的多动能并网逆变器控制策略图，分析内环控制系统中的被控对象，并给出系统被控对象的框图，如图5 所示。

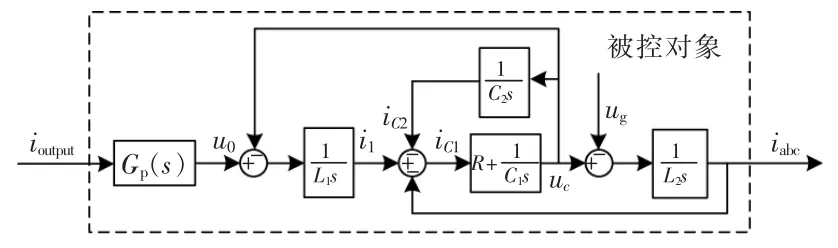
图5 系统被控对象框图Fig.5 Block diagram of the controlled object of the system

图5 中：u0为逆变器出口电压；uc为 u0经过逆变器侧电感 L1后的电压；ug为网侧电压；GP（s）为PWM 逆变器的增益。

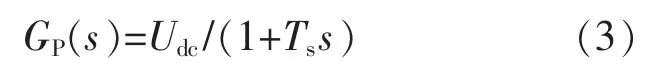
在不考虑ug扰动情况下，被控对象的传递函数为

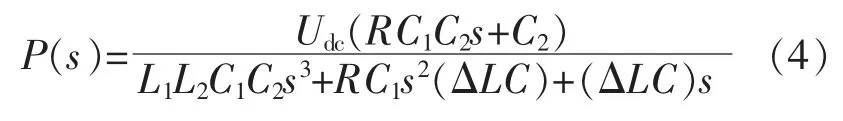
式中：△LC=L1L2+L1C2+L2C2。

在系统相关元件参数确定后，被控对象的传递函数就可以确定。

3.2 改进重复控制器设计及性能分析

重复控制内模由延时时长为一个基波周期T的延时环节经正反馈作用后得到。然而，基波周期延时环节e-sT在实际应用过程中难以实现，本文采用图6 所示的离散域重复控制内模，图中N 为每基波周期采样次数。

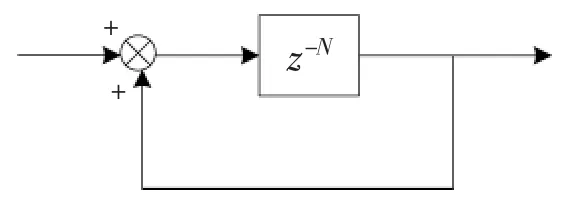
图6 离散域重复控制内模Fig.6 Internal modes of discrete domain repetitive control

为防止因选用入网电流作为反馈量而出现的系统谐振问题，本文选用iabc作为电流反馈量。 同时为实现对参考信号的无稳态偏差跟踪，重复控制将该信号产生的模型作为控制器的一部分放置在闭环中，通过增加前馈通道，与重复控制器的输出信号一起作用被控对象，来改善系统对突加控制指令的响应速度。 图7 为本文设计的改进型重复控制器结构框图。

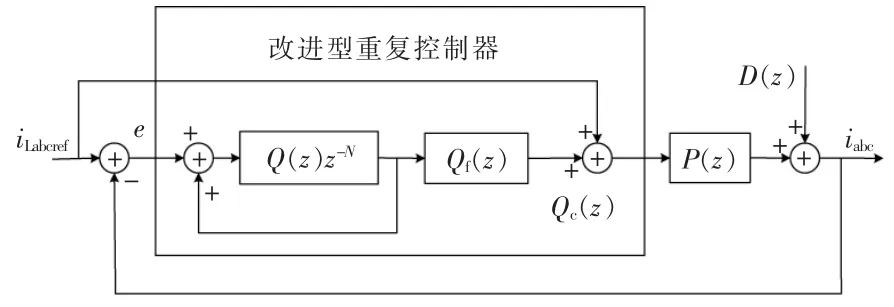
图7 改进型重复控制器结构框图Fig.7 Structure block diagram of the improved repetitive controller

如图7 所示，参考电流和并网逆变器输出电流分别作为改进型重复控制器的输入和输出，其中：P（z）为被控对象；D（z）为周期性扰动信号；Gf（z）为针对被控对象设计的参数可调的补偿器，一般理想的补偿器为 Gf（z）=P-1（z）；Gc（z）为改进重复控制传递函数。

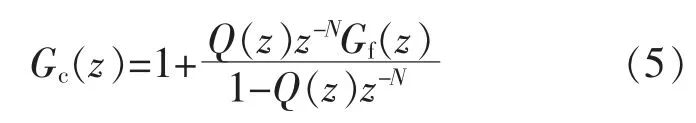
系统从输入到输出的闭环传递函数为

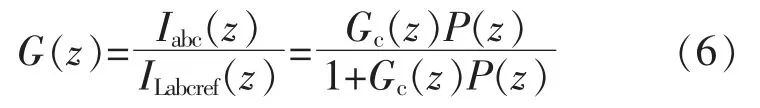
式（6）中，分母为闭环传递函数的特征多项式S（z），即：

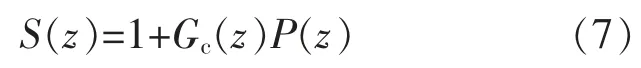
由式（5），（7）可得：

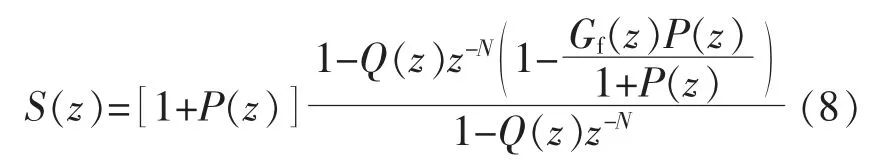
根据S（z）分析闭环系统的稳定性。 为了便于分析，可取式（8）中的z-N值为1，当改进重复控制传递函数稳定时，由小增益定理，使得系统闭环稳定的条件为

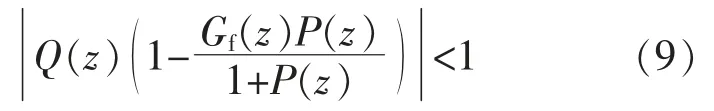
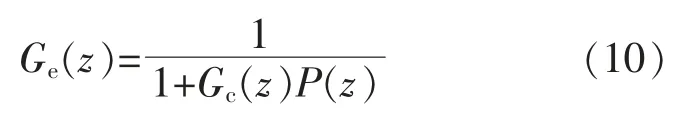
由式（5），（10）可得：

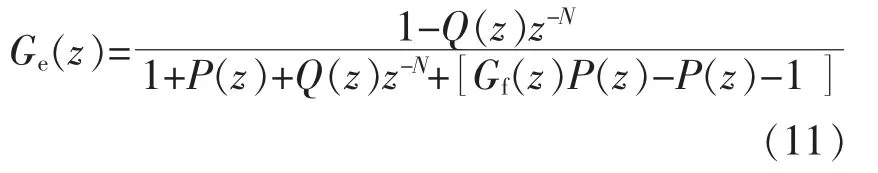
式（11）中，当 Q（z）=1 时，Ge（z）=0，闭环系统的稳态误差为0，但Q（z）=1 不满足闭环系统对稳定性的条件，说明重复控制器在稳定性和稳态控制性能之间存在矛盾。故Q（z）的设计应该是控制器的稳定性和稳态控制性能的折中，在满足系统稳定的条件下尽可能地满足参考和扰动信号的跟踪误差最小化。

3.3 模糊自整定PI控制器性能分析

经改进后的重复控制可确保输出波形符合给定波形，但由于其滞后一个参考周期，所以在获得控制指令后不会立即输出。 当系统内部干扰严重时，重复控制器会对输入指令不作任何反应，这将会极大地影响内环控制器的性能。

为解决重复控制器的动态性能问题，本文引入模糊自整定PI 控制，与改进重复控制形成复合控制。 基于模糊控制的PI 参数自整定解决了PI控制参数固定的问题，使得PI 参数能够根据控制器输入输出偏差和偏差变化率在线调整，使调节范围更宽，提高了控制效果，其复合控制图如图8所示。

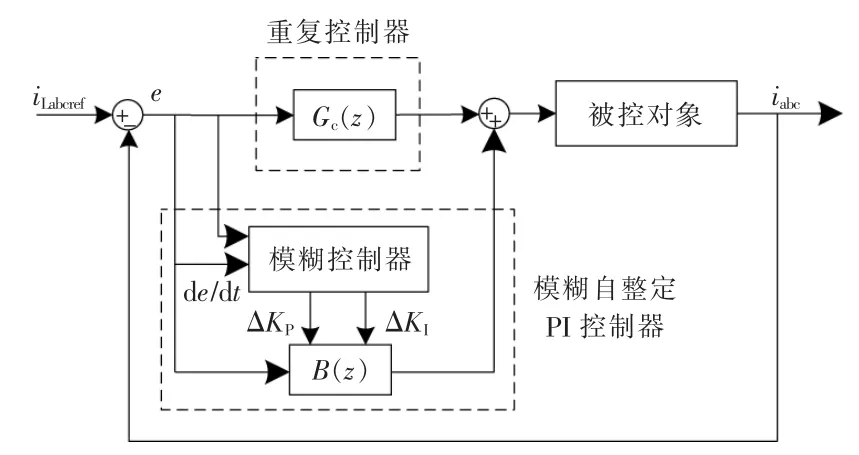
图8 复合控制器系统图Fig.8 System diagram of composite controller

3.4 改进型重复控制器参数设计

3.4.1 Q（z）的设计

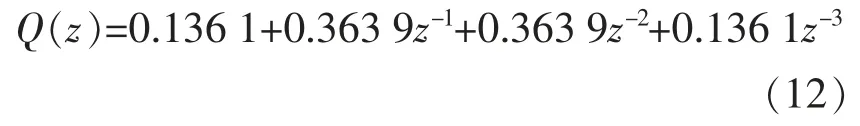
3.4.2 补偿器 Gf（z）的设计

除Q（z）外，根据稳定条件同时兼顾补偿器Gf（z）参数的设计，本文改进重复控制补偿器主要由陷波器、 二阶低通滤波器和超前环节三部分组成。

陷波器的结构为

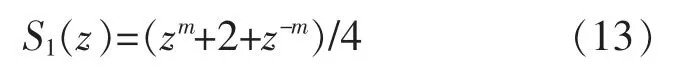
式中：m 为陷波器阶数。

根据设计准则，取中频段的谐振点为第一个陷波点，系统采样频率为10 kHz，得出m=2.36，取整后m=2。

为实现系统能在高频段衰减，采用二阶低通滤波器来增强其高频衰减能力，解决陷波器只能在陷波点附近处产生高频衰减的弊端。 本文滤波器阻尼比设置为0.707，滤波器转折频率值为2π×2.5×103rad/s，在连续域内利用双线性变换法二阶低通滤波器进行离散化，得到：

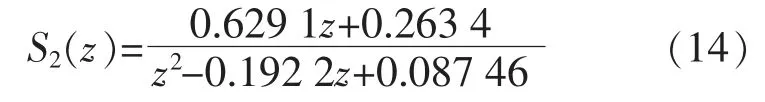
但二阶低通滤波器会产生相位滞后的问题，为对其进行补偿，本文采用7 拍超前环节z7补偿，则补偿器 Gf（z）为

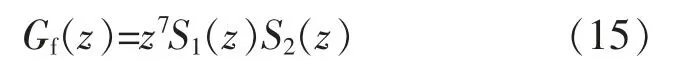
经过补偿后的重复控制各部分以及多功能并网逆变器控制系统Bode 图的幅频曲线与相频曲线如图9 所示。

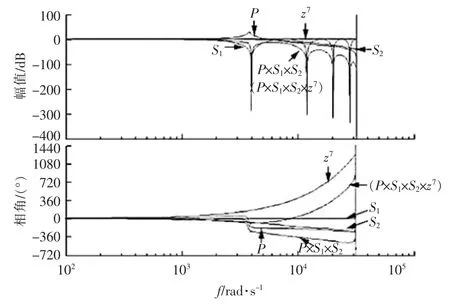
图9 补偿后的重复控制各部分以及多功能并网逆变器控制系统Bode 图Fig.9 Bode diagram of the compensated repetitive control parts and the multi-function grid-connected inverter control system

如图9 所示，在并网逆变器幅频曲线与相频曲线中，当 P 点处于谐振峰值时，Gf（z）中的陷波器幅相频曲线S1处于其最大衰减处，陷波器对逆变器的谐振尖峰起到很好的补偿作用。其中，采用7 拍超前环节 z7的补偿效果如曲线 P×S1×S2×z7所示，与未用补偿曲线 P×S1×S2相比，超前补偿环节在中低频段的相位补偿效果较好。

3.5 模糊控制器设计

模糊PI 自整定控制器的设计思路与步骤如下： 将逆变器输出电流iabc跟随参考电流iLabcref的误差e 及其误差变化率Δe 作为自整定控制器的输入，PI 参数的变化量ΔKP和ΔKI作为控制器的输出；以系统传递函数和变换器数学模型为依据，确定PI 控制的初始值KP0和KI0。

首先，将控制器输入量与输出量分为{NB，NM，NS，ZE，PS，PM，PB}7 个语言值，分别代表{负大，负中，负小，零，正大，正中，正小}，反映出输入与输出偏差的大小与方向。 对于比例控制项KP，其作用是成比例地反映控制系统的误差信号e。当误差产生时，控制器立即产生控制功能以减少误差。 而KP过大会引起系统震荡，破坏系统动态性能，因此，需要正确选择KP值。 当e 较大时，KP取大值以提高响应速度； 当e 较小时，KP值减小防止超调过大产生振荡； 当e 很小时，KP应继续减小以尽快稳定系统。 同时，也要考虑Δe，当Δe和e 同号时，输出偏离稳定值，应适当增大KP；反之，则应适当减小KP。 积分控制项KI控制原理与KP类似。 最后，根据工程控制经验，建立e 和Δe对ΔKP和ΔKI的模糊控制和调整规则，如表1、表2 所示。

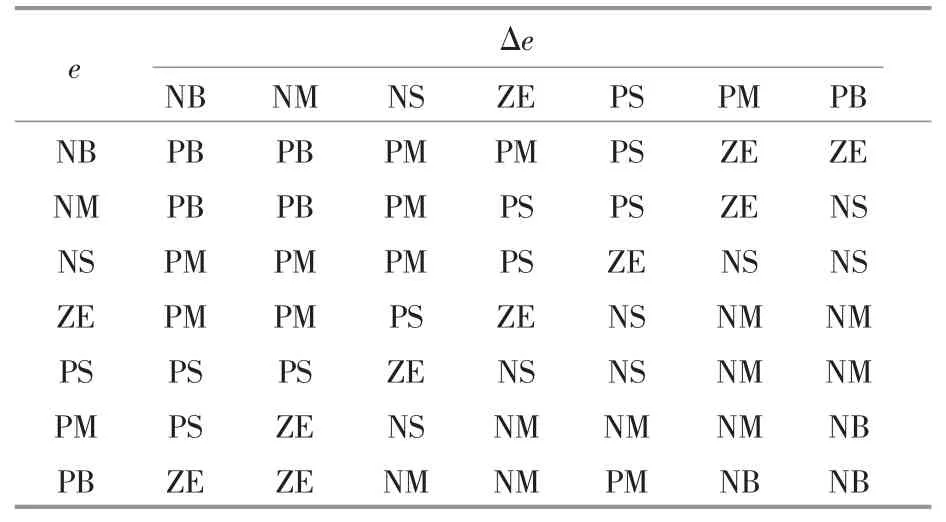
表1 ΔKP 模糊控制规则Table 1 ΔKP fuzzy control rules

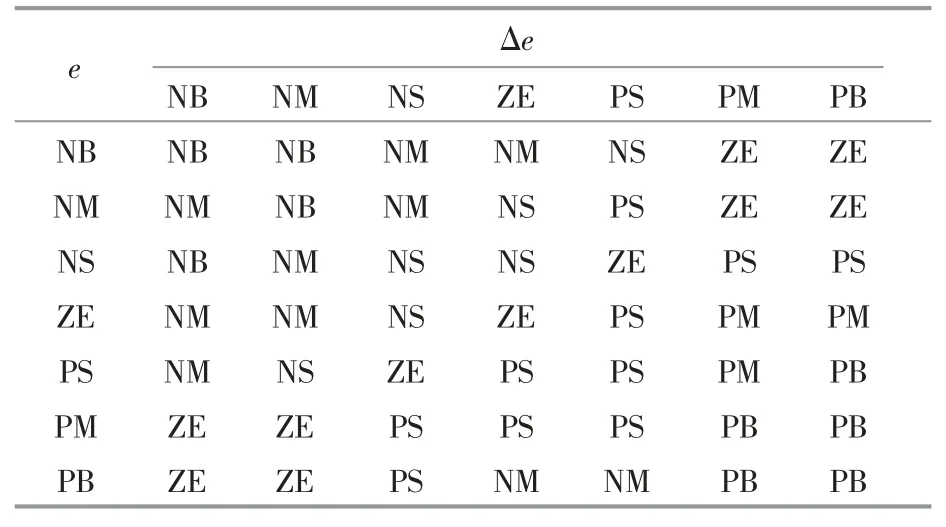
表2 ΔKI 调整规则Table 2 ΔKI fuzzy control rules

4 仿真验证

本文利用PSCAD/EMTDC 软件，对所提的基于改进型重复控制算法和模糊PI 自整定的多功能并网逆变器的正确性和实用性进行仿真验证，并网逆变器相关参数如表3 所示。

表3 多功能并网逆变器参数Table 3 Multifunctional grid-connected inverter parameters

续表3

4.1 无功电流补偿

当本地含无功负荷时，并网逆变器能够在传输有功功率的同时，补偿本地负荷所需的无功功率。 在仿真软件本地负载模块中只投入电感值相同的三相感性负载，用于模拟实际电网中的无功电流，并网逆变器在投入无功补偿模块前后并网电流、电压波形如图10 所示。

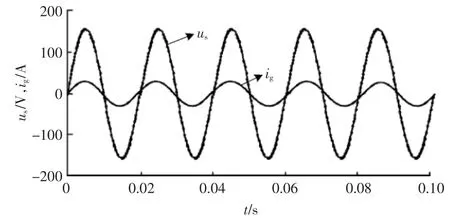
图10 逆变器无功补偿前后并网波形Fig.10 Simulation waveform of reactive power compensation

由图可知： 多功能并网逆变器在0.05 s 前未投入无功补偿模块，在并网点逆变器并网电压和电流存在相位差；0.05 s 时，并网逆变器投入无功补偿控制模块，逆变器迅速调整输出电流，此时并网电压、电流保持同相位，说明补偿控制模块有效改善了并网点的无功问题。

该仿真结果表明，本文所提基于改进重复控制和模糊PI 算法的多功能并网逆变器能够在传输有功功率的同时，补偿本地负荷所需的无功功率，可有效改善电网内的电能质量问题。

4.2 动态响应

在仿真软件中分别搭建基于传统重复控制以及基于改进型重复控制和模糊PI 自整定的系统模型，比较两者在系统参考电流幅值突变时，控制器输出电流跟随参考电流的响应能力，其响应波形如图11 所示。

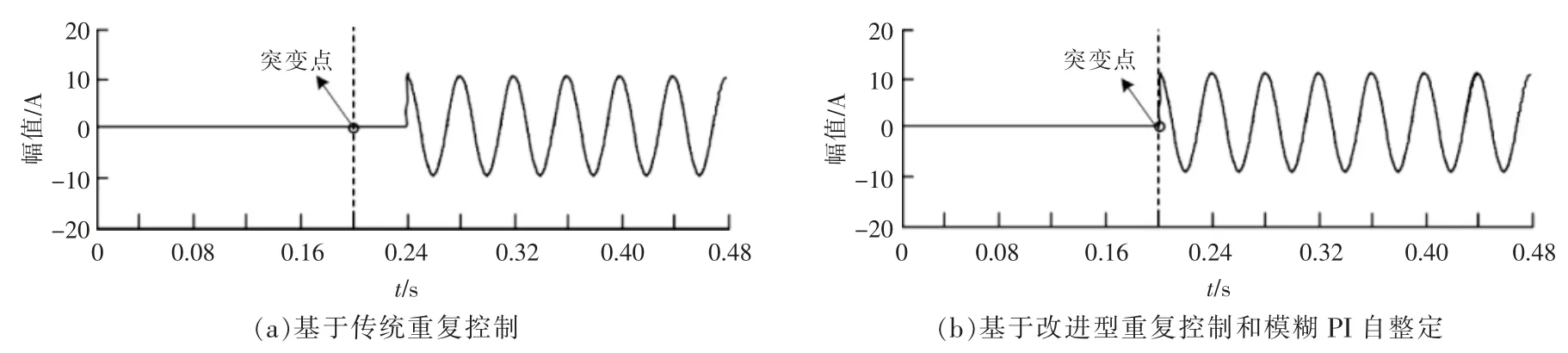
图11 基于传统重复控制以及改进型重复控制和模糊PI 自整定动态输出响应波形Fig.11 Dynamic output response waveform based on traditional repeat control，improved repeat control and fuzzy PI self-tuning

由图可知，当iLabc在0.2 s 时幅值发生突变，正弦波的幅值由0 A 跃变为10 A，参考电流跃变过程发生后，基于传统重复控制的系统需要经过0.04 s 的延时才能响应参考电流的变化并跟随参考电流。 而本文设计的改进重复控制系统能够在突变瞬间响应参考电流的变化，且相对于传统重复控制器具有更高的稳态跟踪精度。

4.3 谐波情况下的无功治理

为验证所设计的多功能并网逆变器在电网谐波情况下仍具有较高的无功补偿能力，在仿真软件本地负载模块中投入三相不可控整流桥，模拟电网中的谐波问题。 图12 为无功负载投入前后，多功能并网逆变器输出电流、电压动态变化波形。

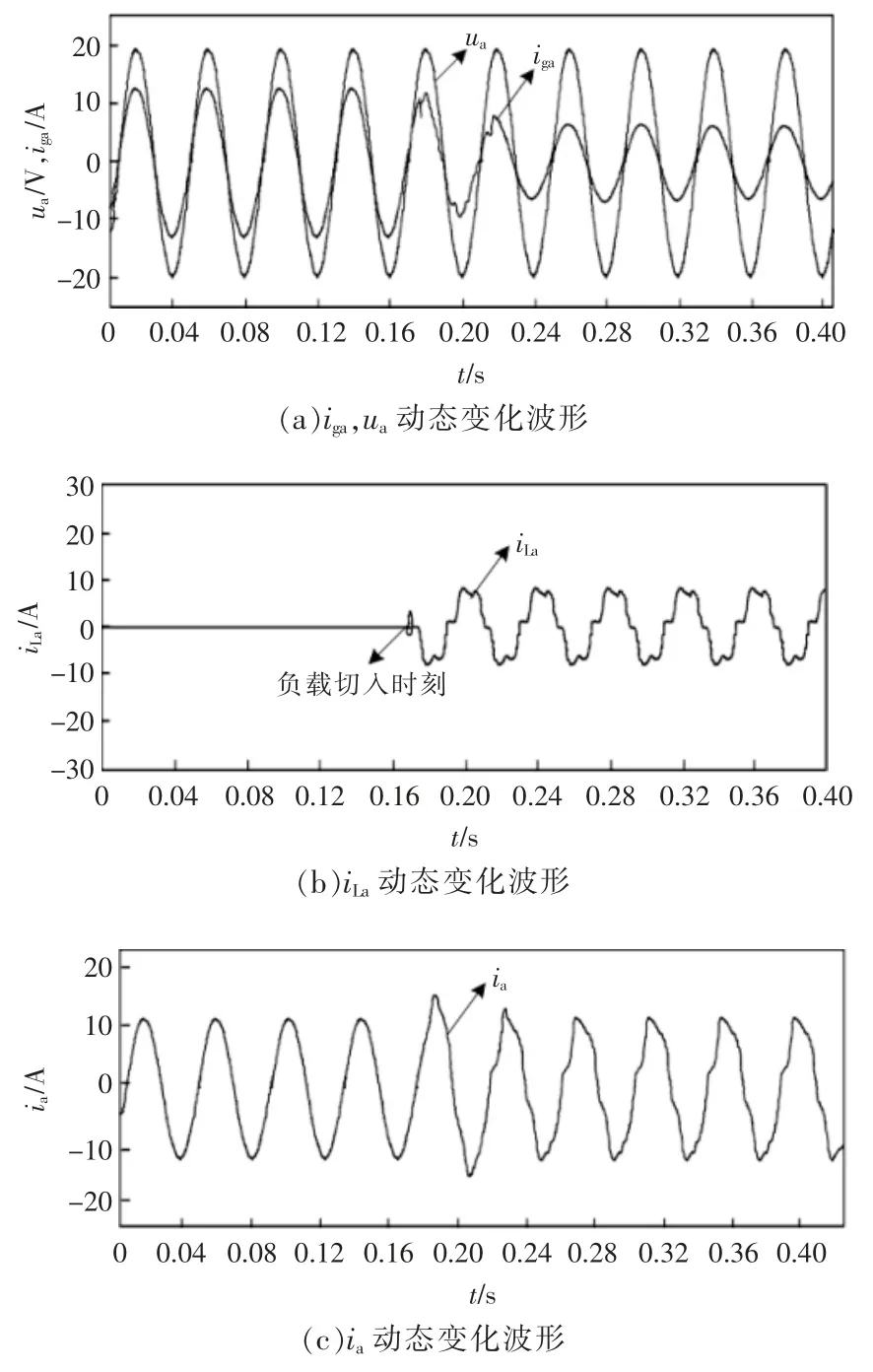
图12 无功负载投入前后iga，ua，iLa 及ia 动态变化波形Fig.12 Dynamic waveforms of iga，ua，iLa and ia before and after reactive load input

由图 12（a），（b）可知，在本地无功负载投入前，并网逆变器iga具有较高的正弦度。 这是因为本次设计的多功能并网逆变器中引入SSIF，抑制了电网谐波对电流的影响，同时iga与ua的相位基本保持一致。当本地负载投入后，多功能并网逆变器输出电流迅速响应负载电流变化，补偿本地负载所需的无功分量，约1 个周期后，入网电流正弦度恢复到负载投入前的水平，入网电流、电压保持同相位。

由此可见，本文所设计的多功能并网逆变器在负载变化时，能够在电网存在谐波时，对无功进行快速精确补偿，从而实现对电能质量的快速精确治理。

5 结论

本文对模糊PI 自整定和改进型重复控制的三相逆变器并网进行了相关研究，提出并网逆变器的主电路拓扑和控制策略，采用基于SSIF 的电流检测方法和瞬时无功功率理论，补偿本地无功功率。运用改进型重复控制器和模糊PI 自整定对参考电流的组合进行控制，在确保系统稳定的前提下，既满足了系统的稳态精度的要求，也保证了系统具有较快的动态响应。