电动汽车的双向DC-DC变换器多模态控制方法

王贵龙，唐 杰，邵 武，邹陆华

（1.邵阳学院 多电源地区电网运行与控制湖南省重点实验室，湖南 邵阳 422000； 2.湖南大学 电气与信息工程学院，湖南 长沙 410000）

0 引言

近年来，全球资源和生态环境的压力不断增大，开发新能源，实现能源的可持续发展已受到普遍关注。 实现新能源开发及能源的可持续利用，都需要大功率的电子元件作为技术支撑。

DC-DC 变换器技术可以将一种形式的直流电转换为另一种形式的直流电，主要用于对电流、电压进行变换，在电力系统、航空航天、计算机交流通信、工业控制、储能系统、电动汽车以及可再生能源等众多行业和领域应用广泛[1]。 由于DC-DC 变换器的功率开关一般都是单向的，在通常情况下，DC-DC 变换器都是单向工作，并且主功率回路装置上的导电二极管也都是单向的，因此DC-DC 变换器控制的能量只能进行单向流动[2]。 但是，在电力系统二次电源充、放电过程的许多应用场景，通过DC-DC 变换器的能量是两个方向流动的，单向DC-DC 变换器不能满足实际应用要求。 双向DC-DC 变换器可以在保持DC-DC 变换器两端直流电压极性不发生变化的前提下，根据电力系统的需要改变电流的方向，对电力系统能量的双向流动进行变换[3]。

双向DC-DC 变换器在电动汽车领域得到了广泛应用，但在行驶状态进行切换时存在功率波动较大的问题。因此，对电动汽车行驶状态切换过程中功率波动进行平抑成为研究热点。 文献[4]提出了鲁棒反演滑模控制方法，建立了等效电路模型，设计了DC/DC 变换器主电路，并针对电池组充放电状况及鲁棒反演滑模控制方法下的输入电压扰动进行了分析。 文献[5]提出了一种基于CMAC神经网络算法的控制方法及模型，在设计CMACPID 控制器模型的基础上，用遗传算法整定PID参数、 用前馈型CMAC 神经网络抑制DC-DC 转换器的非线性干扰。 文献[6]提出了一种利用模糊控制理论，对电压、电流进行双环模糊控制，在分析交错并联DC/DC 变换器工作原理后，利用模糊PI 控制器进行精准控制。 以上方法并没有取得预期的理想效果，存在无法有效抑制变换器功率波动的缺陷和稳定性较差、响应速度慢等缺点。

基于此，本文提出了一种基于多模态控制技术的双向DC-DC 变换器控制方法。 本研究分析了电动汽车双向DC-DC 变换器的拓扑结构、升降压控制模式以及电压和电流模式控制，并得到电压和电流的开、闭环函数，利用多模态控制方法实现对功率波动的平抑控制。

1 基于多模态控制技术的双向DC-DC变换器控制方法

1.1 双向DC-DC变换器的拓扑结构及工作原理

双向DC-DC 变换器拥有多种拓扑结构，其中Buck-boost 双向DC-DC 变换器具有拓扑结构简单、控制简便和可靠性较高的优点，能够满足当前电动汽车对能量转换的特殊要求[7]。 图1 为双向DC-DC 变换器的拓扑结构示意图。 图中：C1为低压侧电容；C2为高压侧电容；L1为电感；Q1，Q2为全控开关器件 IGBT；R 为电阻；D1，D2为续流二极管；V1为蓄电池电压；V2为输出电压。

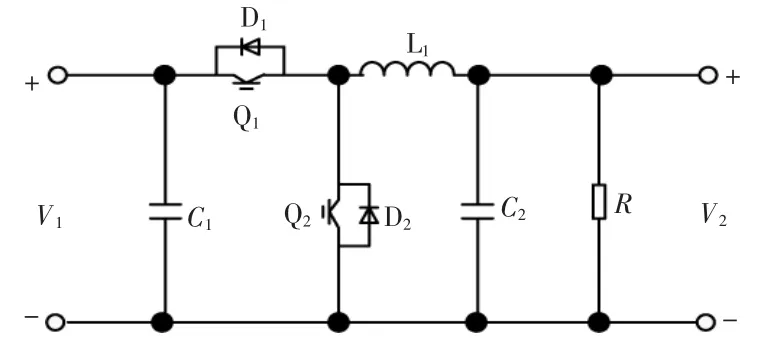
图1 Buck-boost 双向DC-DC 变换器的拓扑结构示意图Fig.1 Buck-boost topology diagram of bidirectional DC-DC converters

当电动汽车处于运行状态，需要高压启动或提速时，电动汽车本身电池的电压无法满足这一要求，双向DC-DC 变换器须采用升压模式运行。保持拓扑结构中的Q2关断，Q1导通，双向DCDC 变换器的电感L1迅速储存能量，C2作为电动汽车的电源负责启动或提速供电。 Q1关断时，双向DC-DC 变换器的蓄电池电压V1和电感L1共同作用于电动汽车，为负载供电。 在Q1关断的一个周期内，电动汽车高压侧输出电压V2：

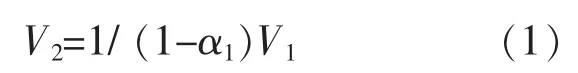
式中：α1为 Q1的占空比。

通过对该参数的调节，能够使电动汽车输出电压更加稳定，同时实现电动汽车的能量转换。图2 为Buck-boost 双向DC-DC 变换器的升降压控制示意图。

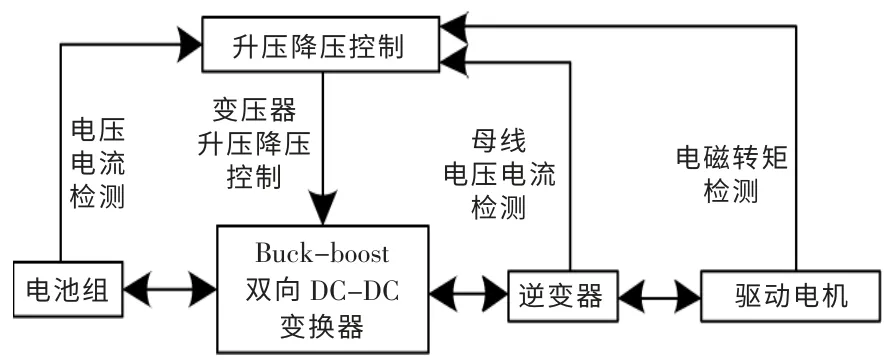
图2 双向DC-DC 变换器的升压和降压控制示意图Fig.2 Boost and Buck control diagram of bidirectional DC-DC converter

1.2 不同工况下电动汽车双向DC-DC变换器工作状态

通常情况下，电动汽车的工况包括停车、起步、匀速行驶状态、加速行驶状态、减速行驶状态、轻载状态、重载状态等。 由于电动汽车运行工况的差异，双向DC-DC 变换器的拓扑结构形式也有所不同，其工作原理也不尽相同[8]。设Pcm和Pmcc分别为电动汽车双向DC-DC 变换器的电磁功率和负载功率；T 和ω 分别为电动汽车双向DC-DC 变换器的机械转矩和机械角速度，则：

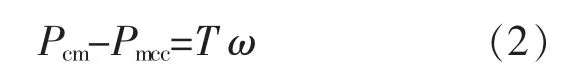
采用上式计算，如果Pcm＞Pmcc，表示电动汽车正处于起步运行状态或加速运行状态。此时，电动汽车双向DC-DC 变换器电磁功率的部分能量用于抵消电动汽车负载功率，剩余能量用于电动汽车提速，电池向电动汽车电机输出功率。 双向DC-DC 变换器作为电动汽车电源与电机驱动系统中间的能量控制转换单元，处于升压运行模式，须要提升电动汽车的电池电压等级，以使电动汽车驱动系统的直流母线电压提升到足以满足起步或加速运行的设定值要求。

如果Pcm=Pmcc，表示电动汽车处于匀速运动状态，电动汽车电机输出的电磁功率与输出的机械功率等效，汽车电磁转矩与负载转矩之间处于平衡状态，能够保证电动汽车匀速行驶。 此时，电动汽车双向DC-DC 变换器处于升压运行模式下，能量从电池侧向电机侧流动。

如果Pcm＜Pmcc，表示电动汽车处于减速运动状态或初始制动状态。 此时，电动汽车双向DC-DC变换器处于降压运行模式，电动汽车的电磁功率要小于机械功率，电动汽车驱动电流方向为负，能量从电机侧向电池侧转移。

1.3 多模态控制技术下的变换器控制

通过上述分析显示，电动汽车双向DC-DC变换器随运行状态的变化而不断改变控制方式，有效实现多模态控制。

（1）双向DC-DC 变换器的电压模式控制

双向DC-DC 变换器以输出电压作为电动汽车反馈信号，构成电动汽车单闭环电压型控制系统（图 3）。

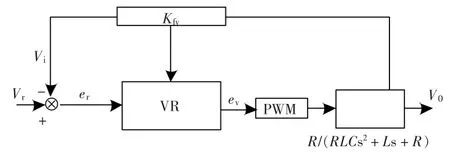
图3 电动汽车单闭环电压型控制系统架构Fig.3 Architecture of single closed-loop voltage control system for electric vehicle

图3 中，VR 为电动汽车双向DC-DC 变换器的电压环调节器；R/（RLCs2+Ls+R）为双向DCDC 变换器的 LC 滤波函数；Kvp+Kvi/s 为 PI 控制器双向DC-DC 变换器的电压调节传递函数。

将电动汽车的脉冲宽度调制功率转换环节视为比例环节，设置比例系数为 KPWM，Kfv，KPV，KVi为电动汽车的电压控制参数，则电动汽车双向DCDC 变换器电压开闭环传递函数计算公式如下：

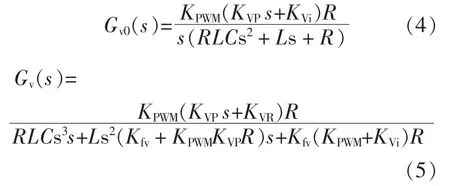
由于电动汽车的双向DC-DC 变换器为二阶振荡环节，电动汽车单闭环电压型控制系统可以等效为三阶模型，如果KVi=0，电动汽车单闭环电压型控制系统可以等效为二阶模型，但在功率波动平抑中有响应速度慢，稳定性较差的缺点[9]。

（2）双向DC-DC 变换器的电流模式控制

为了克服上述双向DC-DC 变换器的电压模式控制方法在电动汽车功率波动平抑中存在的缺点与不足，提出一种改进电流型控制模型[10]。在上述电压控制模式基础上，对电动汽车运行状态进行反馈校正，以电动汽车输出的电感电流作为反馈向量，构成变换器电流内环。 双向DC-DC 变换器的电流控制模式包括峰值电流控制模式、 平均电流控制模式和电荷控制模式[11]。 在双向DC-DC变换器峰值电流控制模式中，电动汽车电感电流的峰值与平均值的比例与电动汽车驱动电路占空比具有相关性。在给定条件一致的情况下，电动汽车驱动电路占空比发生变化时，电动汽车的电感电流也会随之发生变化，无法对电动汽车电感电流或输出电流进行精确控制[12]。双向DC-DC 变换器的平均电流控制模式中，由于电动汽车电路存在反馈网络积分环节，可以使得电动汽车电感电流平均值与电流给定值相等，从而实现电动汽车输出电流的高精度控制。 对于双向DC-DC 变换器的电荷控制模式，电动汽车单闭环电压型控制系统存在分频震荡现象，可以通过调节电动汽车电流调节器PI 参数来消除分频震荡。 双向DCDC 变换器平均电流控制模式的系统特性如图4所示。

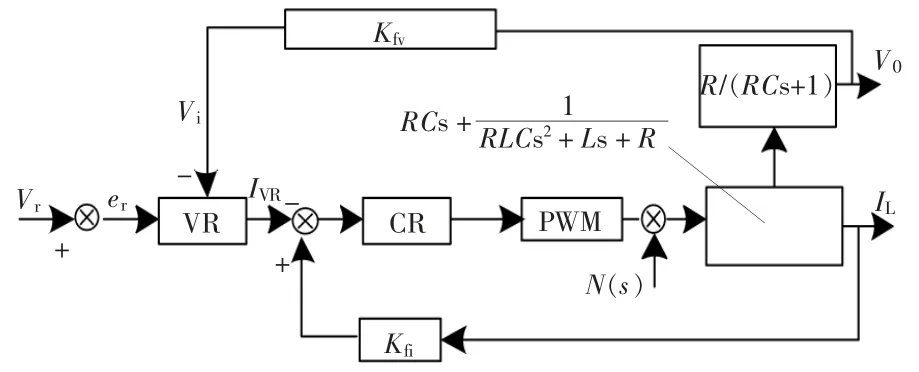
图4 电动汽车双闭环电流型控制系统架构Fig.4 Architecture of dual closed-loop current control system for electric vehicle

图4 中，CR 为电流环调节器。

根据图4 可得电动汽车双向DC-DC 变换器电压开闭环传递函数计算公式：

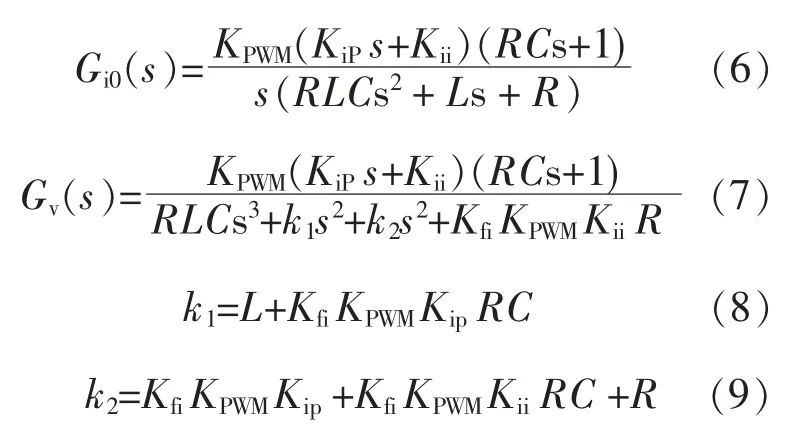
式中：KiP，Kfi，Kii为电动汽车的电流 PI 控制器参数；KiP+Kii/s 为PI 控制器下双向DC-DC 变换器的电流调节传递函数。

根据上述分析可知，电动汽车双向DC-DC变换器电压开环传递函数中有两个零点，可以等效为双向DC-DC 变换器电流环的一个比例环节Gi（s）=1/Kfi。将图4 的架构简化，可得到简化后的双向DC-DC 变换器电压环等效结构图（图5）。

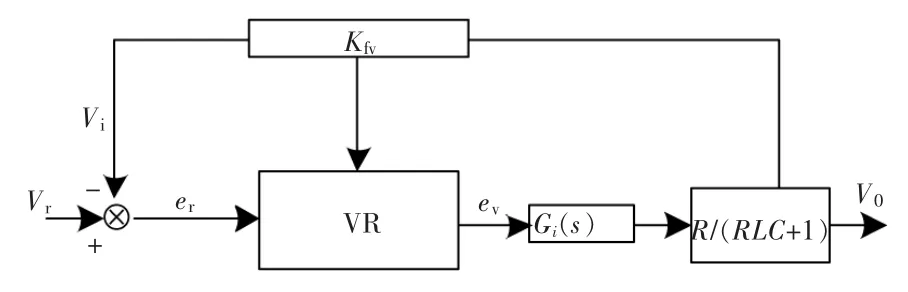
图5 简化后的双向DC-DC 变换器电压环等效结构图Fig.5 The equivalent structure diagram of the voltage ring of the simplified bidirectional DC-DC converter

根据图5 可得化简后的电动汽车双向DCDC 变换器电压开闭环传递函数计算公式：

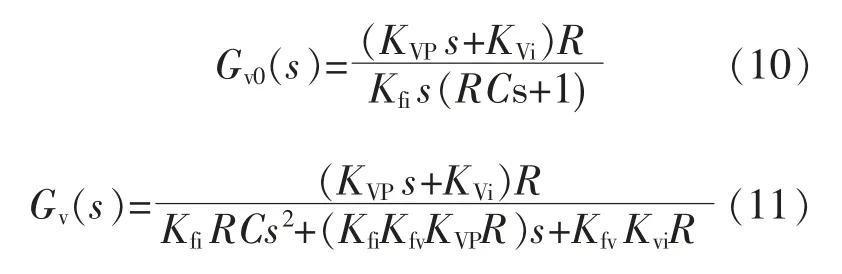
根据上述计算可知， 电动汽车双向DC-DC变换器是一阶惯性环节，可以将电动汽车单闭环电压型控制系统等效为一个二阶模型。 当Kvi=0时，变换器电压环的相角稳定裕量逼近90 °。 此时控制系统响应速度较快，变换器电流跟踪能力强。

在上述基础上， 为电动汽车双向DC-DC 变换器设计一个功能控制单元。 定义该功能控制单元的闭环开关为

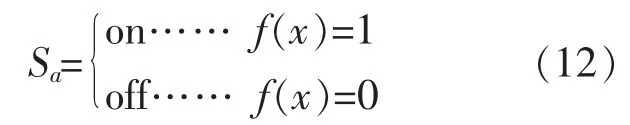
式中：x 为该功能控制单元控制方式的取值；a=1，2。

假设电动汽车双向DC-DC 变换器功能控制单元的用户设定的电压信号和电流信号分别为 Uset和 Iset，电动汽车双向 DC-DC 变换器功率设置可以转换为Uset×Iset。 可以通过计算功能控制单元电动汽车双向DC-DC 变换器的电压环给定信号和电流环给定信号， 对功率波动进行平抑。

综合上述对双向DC-DC 变换器的电压模式控制和电流模式控制， 可完成对DC-DC 变换器的功率波动平抑控制，控制模型表达式为

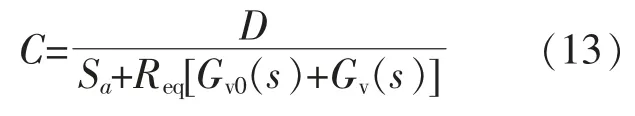
式中：D 为双向 DC-DC 变换器占空比；Req为等效负载。

2 仿真结果分析

为了检验本文提出的基于多模态控制技术的双向DC-DC 变换器控制方法， 在不同工况下平抑电动汽车功率波动的有效性， 采用模拟软件Matlab/Simulink 进行数值模拟。 几种应用较为广泛的电动汽车在启动、制动过程中，双向DC-DC变换器的升压和降压工作模式的具体模拟仿真参数如表1 所示。

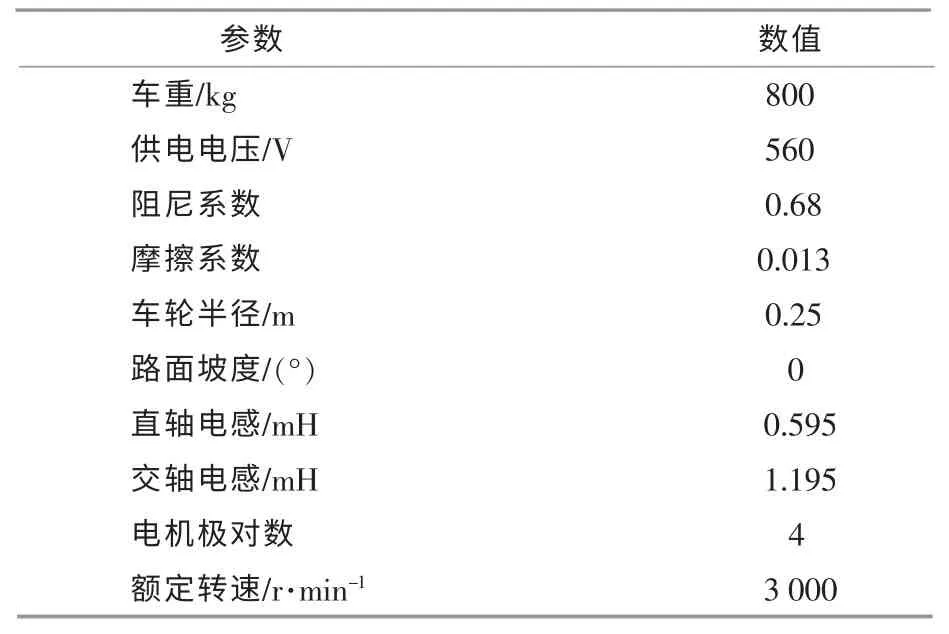
表1 系统仿真参数Table 1 System simulation parameters

采用文献[4]滑模控制方法和本文所提出方法对电动汽车双向DC-DC 变换器进行控制效果的对比测试。图6 给出了双向DC-DC 变换器在Buck 模式下采用两种控制方法的输出电压波形。

从图6 的对比结果中可以清楚地看出，采用本文提出的多模态控制方法时， 在Buck 模式下双向DC-DC 变换器的输出电压在10 ms达到稳定状态；采用滑模控制方法时，在 Buck模式下双向DC-DC 变换器的输出电压在12 ms 之后才能达到稳定状态。 相比较而言，在同等工作模式下，本文提出方法能够有效地提高电动汽车双向DC-DC 变换器的动态响应性能。

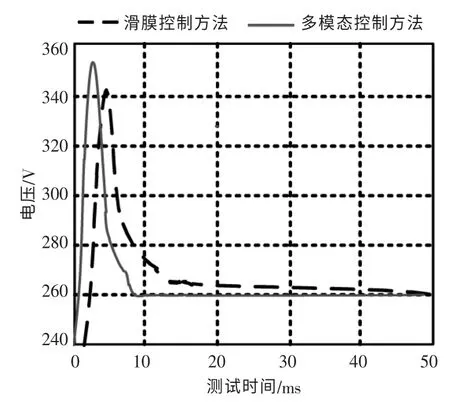
图6 变换器在Buck 模式下两种控制方法的输出电压波形Fig.6 Two control methods of converter output voltage waveform in Buck mode

图7 展示了在Buck 模式下， 采用不同控制方法时， 双向DC-DC 变换器在输入电压跳变时的输出电压波形。

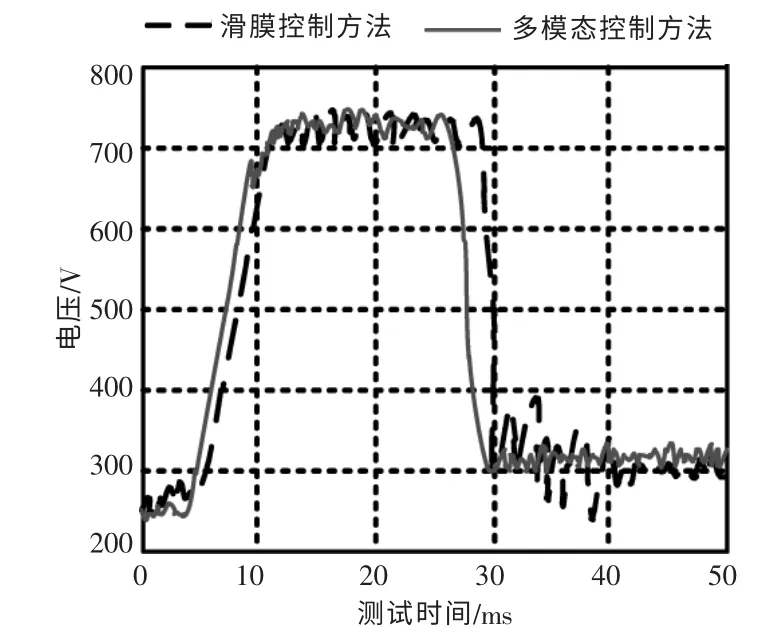
图7 输入电压跳变时，采用不同控制方法输出的电压波形Fig.7 Voltage waveform comparison of different methods output when input voltage jumps

从图7 的实验结果可以看出, 当电动汽车双向DC-DC 变换器输入电压后10 ms 时，电压由250 V 跳变为720 V，多模态控制方法经过30 ms即可将跳变电压恢复稳定状态，而滑模控制方法需要40 ms 才能平抑电动汽车双向DC-DC 变换器的功率波动。由此说明，本文所提出的控制方法能够大大提高双向DC-DC 变换器输入电压的稳定性。

图8 给出了在Buck 模式下采用不同控制方法时，负载跳变对双向DC-DC 变换器输出功率波形的影响。

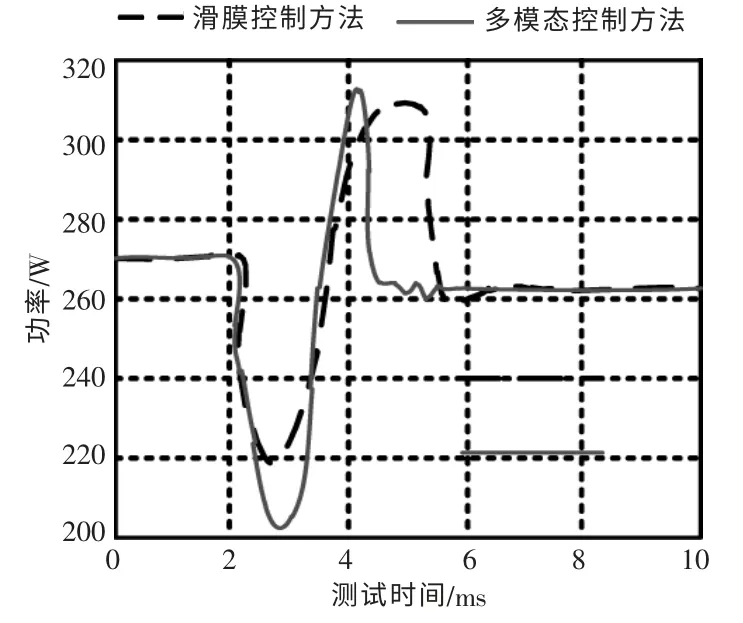
图8 不同方法在变换器负载跳变时的输出功率波形Fig.8 Output power waveform of different methods in converter load hopping

由图8 的实验结果可以看出，电动汽车启动2 ms 之后双向DC-DC 变换器负载开始发生跳变，滑模控制方法需要6 ms 以上才能完成功率波动平抑； 本文所提出的控制方法只需耗时4.2 ms就能将电动汽车双向DC-DC 变换器负载跳变恢复到稳定状态。另外，滑模控制方法在平抑负载跳变过程中存在较大的功率波动，对电动汽车双向DC-DC 变换器负载突变的抗干扰性能相当差。由此说明，本文所提出的控制方法在响应速度方面和抗负载跳变干扰性能方面都具有明显优越性。

3 结束语

针对当前双向DC-DC 变换器控制方法抗干扰性能差，响应速度慢的缺陷，提出一种基于多模态控制技术的双向DC-DC 变换器控制方法。 通过仿真验证表明，在不同工况下，与滑模控制方法相比，本文所提出的控制方法在抗干扰性能方面、稳定性能方面和系统响应速度方面，均显示出优越性与有效性，能够实现电动汽车双向DC-DC变换器功率波动的平抑控制。