计及反射辐射的分布式光伏阵列建模研究

吴佳兵，丁 坤，陈富东，张经炜

（1.河海大学 机电工程学院，江苏 常州 213022； 2.常州市光伏系统集成与生产装备技术重点实验室，江苏常州 213022）

0 引言

光伏发电作为一种重要的可再生清洁能源，近年来发展极为迅速，相比大型光伏电站，小型分布式光伏电站具有因地制宜、分散布局、就近利用的优势。分布式光伏电站所处环境复杂，仅研究局部阴影遮挡下的输出模型远远不够[1]。

前人对平面反射器在集热式光伏中的应用进行了研究，平面聚焦一般用于高纬度地区冬季提高太阳能热系统的产量[2]。 鲜有研究报道建筑立面对分布式光伏电站发电的影响。 常规建材一般为粗糙表面，其反射特性不能用朗伯体或镜面反射体来表征，实际工况中需要对粗糙物体表面散射特性进行研究、运用。自Nicodemus 正式提出双向反射分布函数[3]以来，关于此类反映粗糙物体的吸收、反射系数的函数建模方法被大量提出，如最早的Lambert 模型、后期较精确的Phong 模型、五参数模型等[4]。 目前，这些模型主要应用在计算机图像处理、地物遥感等方面。

本文通过分析往年气象站的大量实测辐照数据，建立适应当地晴空因子与太阳辐射的直散分离比的回归方程，通过此回归方程和水平面总辐射，实现太阳辐射的直散分离。 再结合太阳、建筑物立面的具体位置，得到建筑物立面上所接收的辐照度，类比Phong 模型研究反射辐射方法，得出适应于建筑物立面的反射辐射模型。 通过所建立的反射辐射模型，结合太阳位置、建筑物位置、光伏阵列布局等因素，得到光伏阵列各部分精确的太阳辐照度。接着代入光伏组件数学模型，得到不同辐照影响下的光伏组件输出特性，最终通过叠加法得到光伏阵列的高精度输出特性曲线。

1 反射辐射模型建立与分析

1.1 光伏阵列表面太阳辐射分析

相比于普通光伏阵列，建于屋顶的分布式光伏阵列会受到周围建筑立面的反射辐射。 图1 为分布式光伏阵列受到的辐照度示意图。

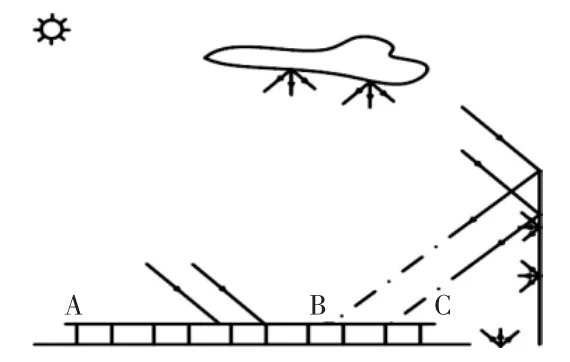
图1 分布式光伏阵列所受辐射示意图Fig.1 Diagram of absorbed irradiation of distributed photovoltaic array

光伏阵列所受到的辐射I 可表示为

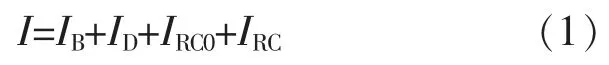
式中：IB为太阳的直射辐射；ID为天空的散射辐射；IRC0为地表反射辐射；IRC为光伏阵列受到来自周边建筑物立面的反射辐射。

1.2 反射辐射模型建立

对于地表反射辐射，有如下计算公式[5]：

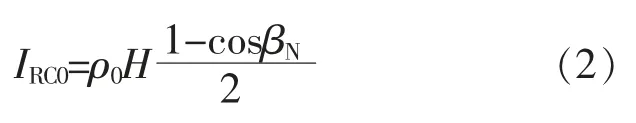
式中：H 为水平面总辐照度；βN为阵列的倾角；ρ0为地表反射率，对于垂直安装的单面光伏阵列，上式表明只接收到一半的地表反射光，一般ρ0取0.2[5]。

对于建筑立面的反射辐射，现代城市建筑物饰面材料常见的釉面瓷砖、外墙涂料、钢化玻璃，其表面光学特性与传统水泥表面、 粉刷墙面的光学特性有显著区别。后者可以认为是漫反射材料，前者夹杂规则反射辐射，属于混合反射材料范畴[6]。 建筑立面（以东西向立面为例）所受到的总辐射IC为直射辐射IBC、散射辐射IDC[7]及反射辐射IRC的和，表达式为

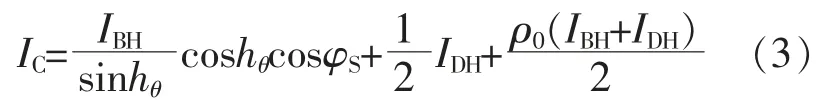
式中：等式右边三项分别为 IBC，IDC[7]，IRC；IBH，IDH分别为水平面直射辐射、 散射辐射；hθ为太阳高度角；φS为太阳方位角。

基于Phong 模型，将建筑立面反射的光束分解成漫反射和镜面反射两个分量。 设定表征漫反射特性的变量为等效漫反射率ρ1，表征镜面反射特性的变量为等效镜面反射率 ρ2，ρ1和 ρ2均需通过实验测定。由朗伯定律可知,漫反射的大小由入射光强度和入射光与立面法线夹角所决定[4]。 以立面底部中心为原点建立空间直角坐标系，所在位置坐标为（x0，y0，z0），阵列所处水平面受到的等效漫反射辐射IRC1为

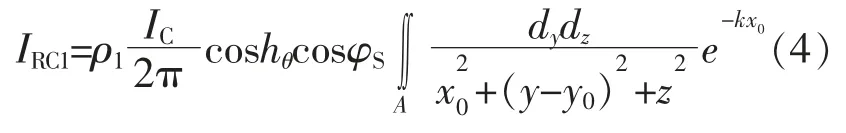
式中：A 为建筑物立面积分域；x0为辐照仪与建筑物立面距离；K 为空气衰减系数，取0.007 632 m-1[8]；分布式光伏阵列中x0一般很小，故本模型中忽略e-kx0一项。

对于受到混合反射的阵列，主要的辐照增强来自建筑立面的规则反射辐射 （立面受到直射辐射的反射）。故位于混合反射下的光伏阵列水平面受到的等效规则反射辐射为

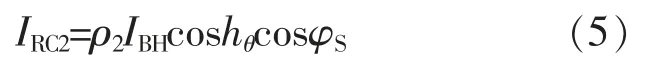
式（3），（5）中，水平面直接辐射 IBH、水平面散射辐射IDH待求解。 这两个分量在水平面总辐射的占比与当地空气质量、天气情况有紧密联系。晴空因子Kt为实际水平面总辐照度H 与水平面天文辐射H0的比值[9]，取值为 0～1，比值越低，表明空气质量越好，能够简便且较为精确地宏观反映一个地区实时的天气质量。 在缺乏实时散射辐射数据的情况下，依靠当地历史存留数据，可将晴空因子与散射透射比建立回归模型，通过水平面总辐照度推算出待求解分量。

水平面天文辐射不考虑大气影响，是由太阳对地球的天文位置而确定的到达地球大气上界的太阳辐射，可表示为[10]

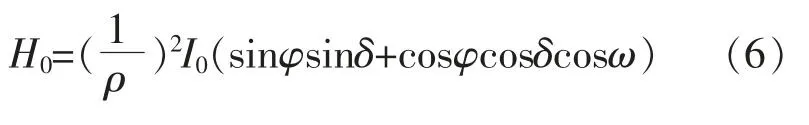
式中：H0为水平面上不考虑大气影响的太阳辐照度，W/m2；（1/ρ）2为日地距离修正系数，无量纲；I0为太阳常数，一般取 1 367±7 W/m2；φ 为测量点地理纬度，rad；δ 为太阳赤纬，赤道以北为正，以南为负，rad；ω 为太阳时角，正午太阳位于正上方取值为 0，向西为正，向东为负，rad。

太阳赤纬和日地距离修正系数均与日期有关，查阅相关文件可获得太阳赤纬与日地距离修正系数[10]。 将太阳时角代入式（6），即可得到白天任意时间地点的水平面天文辐照度。

本文通过随机选取本地气象站2016 年包含各天气情况的50 d 逐时水平面散射辐照度和总辐照度的原始数据，建立直散分离模型。水平面散射辐照度和总辐照度的比值为大气散射透射比Kd，一般 Kd与 Kt近似呈线性变化[11]。图2 为 Kd与Kt的分段拟合。 由图可知：当 Kt为 0～0.30 时，数据分布较为集中； 当Kt为0.30～0.70 时，斜率变大；当 Kt＞0.70 时，变化率变得平缓。 由此表明，通过建立分段回归模型可以获得更高的模型精度。

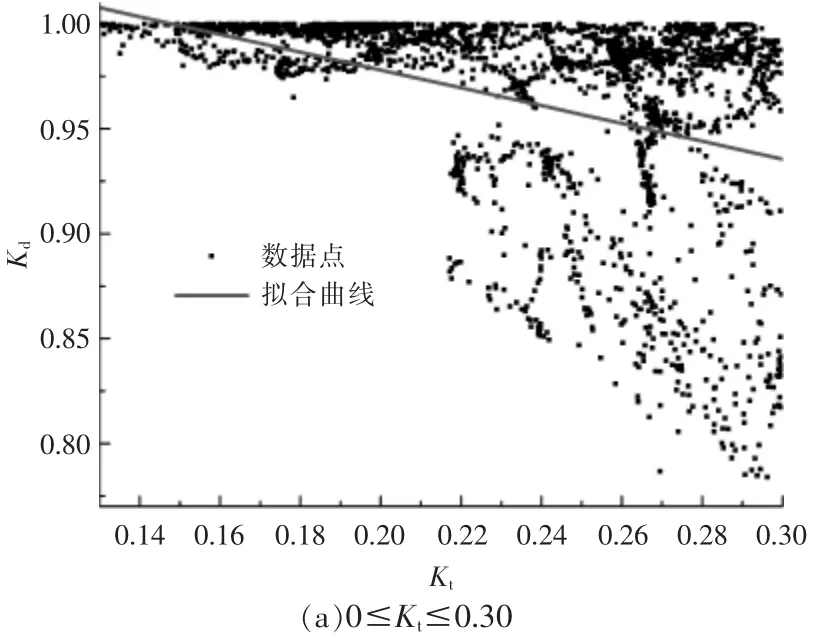
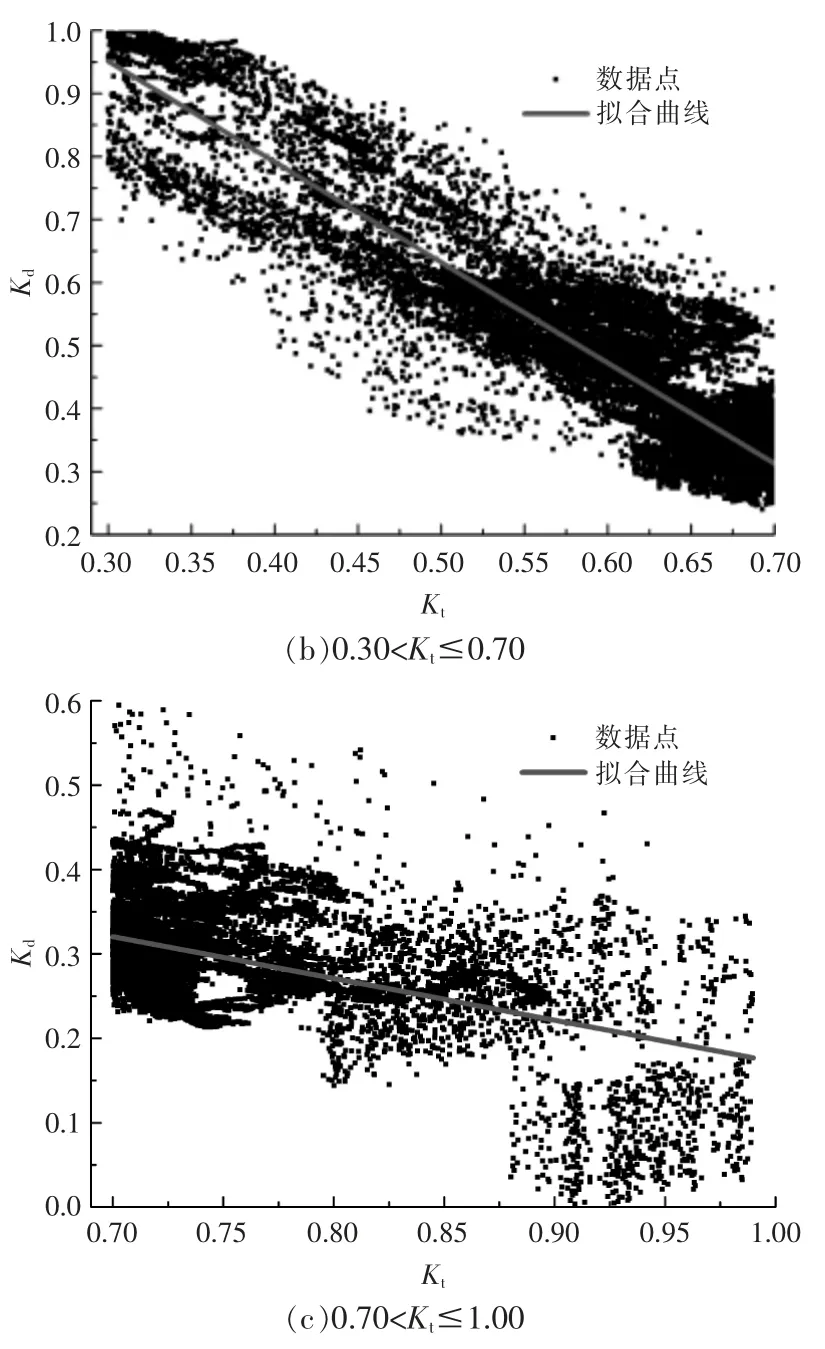
图2 大气散射透射比与晴空因子的分段拟合Fig.2 Piecewise fitting of atmospheric scattering transmittance and clear sky index

经过数据筛选及回归分析后，得到拟合曲线为

将直散分离模型求得的 IBH，IDH代入式（3），（5），再将式（3）代入式（4），最终得到反射辐射理论模型。

1.3 反射辐射模型验证

图3 实验平台Fig.3 Experiment platform

图3 为本文所搭建的反射辐射模型实验平台。实验地点位于东经 119°08′，北纬 31°78′，黄赤交角为 23°26′，时间为 2019 年 5 月 10 日 7：43-9：33。 釉面瓷砖墙壁面正东，高 3.5 m，长 4 m，太阳辐照传感器距离墙壁0.2 m。 图中：一个太阳辐照传感器置于釉面瓷砖立面正下方，用于测量水平面辐照和来自墙壁的规则反射与漫反射增强；因太阳位于墙壁的东南方向，置于墙壁南边的另一个太阳辐照传感器未受到立面规则反射的影响。

图4 为现场实测的混合反射增强、 漫反射增强、无反射增强辐照度数据。

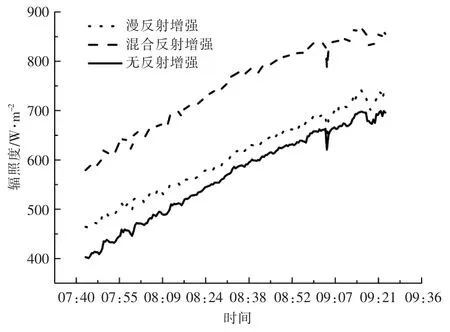
图4 混合反射辐射、漫反射辐射、无反射辐射实测数据Fig.4 Measured mixed reflected, diffuse, and non-reflected radiation data

通过式（4）结合直散分离模型，求得模型中等效漫反射率为0.096。图5 为估算等效漫反射辐射与实测等效漫反射辐照度对比及其相对误差。 由图可知，误差在3%以内。 通过式（5）求得混合反射中的等效规则反射率为0.388 3。 图6 为估算混合反射辐射与实测值对比及其相对误差。 由图可知，误差在3%以内。

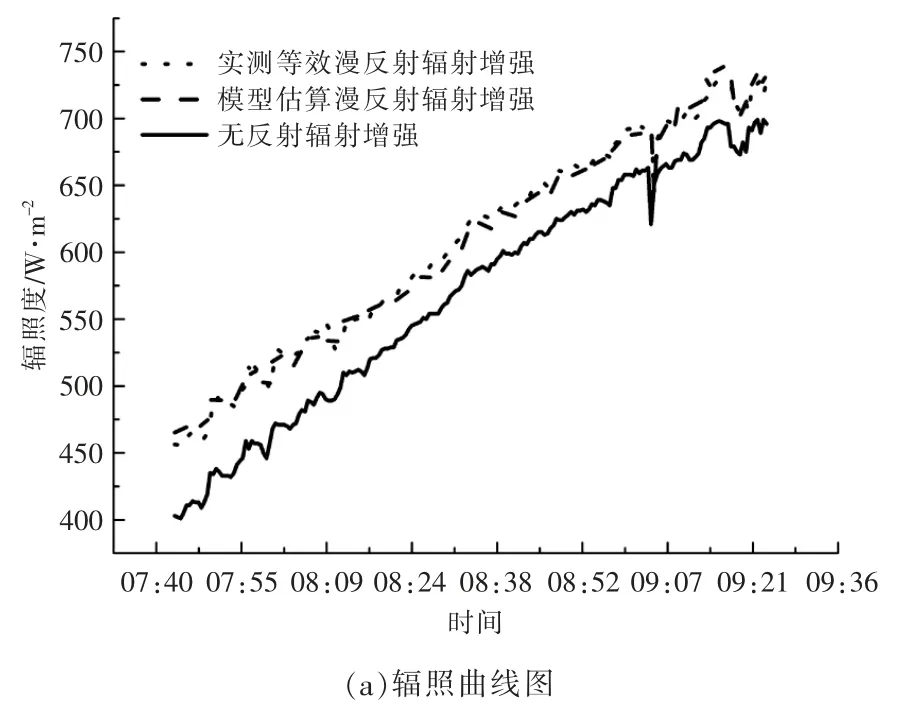
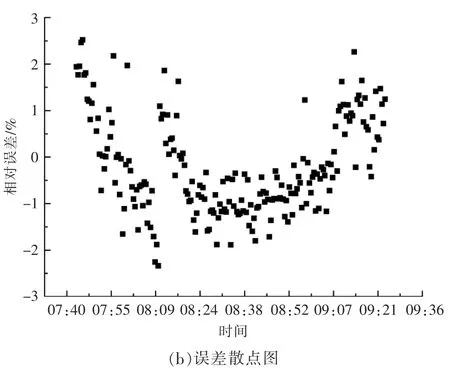
图5 实测等效与估算等效漫反射辐照值对比及其相对误差Fig.5 Comparison of measured and estimated equivalent diffuse reflection irradiance and relative error

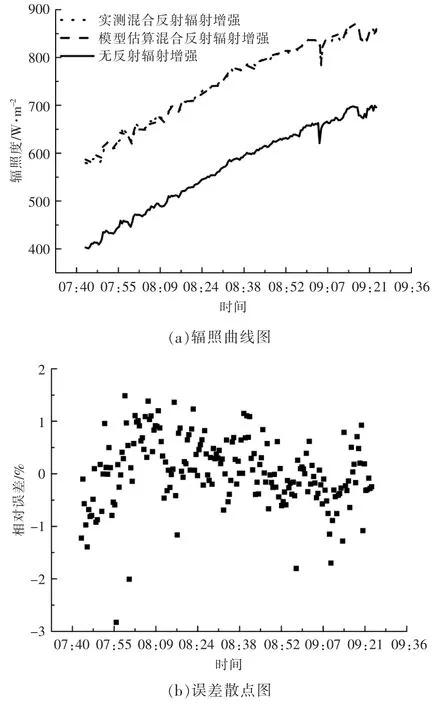
图6 实测与估算混合反射辐照值对比及其相对误差Fig.6 Comparison of measured and estimated hybrid reflection irradiance and relative error

2 计及反射辐射的分布式光伏阵列模型

2.1 计及反射辐射的分布式光伏阵列模型

本文采用光伏组件的五参数模型，代入组件参数和工作环境参数，通过迭代得到光伏组件的电流-电压（I-V）特性曲线[12]。

图7 为计及反射辐射的分布式光伏阵列模型结构，模型同时考虑了阵列排布、组件尺寸、周边建筑距离等实际输出影响因素。首先，根据周边建筑的高度及其到光伏阵列的距离，推算出任意时刻周边建筑对光伏阵列的阴影遮挡或反射增强情况[5]；然后，通过往年历史数据与本文所建立的立面反射辐射模型，结合组件的安装方式，获得计及反射辐射的光伏阵列不同部分的辐照度，根据组件数学模型求出不同辐照度下各个组件的I-V特性曲线；最后，通过叠加法得到整个光伏阵列的输出[13]。

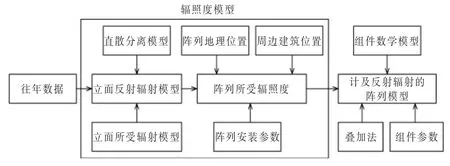
图7 计及反射辐射的分布式光伏阵列模型结构Fig.7 Model structure of distributed photovoltaic array considering reflection irradiation

2.2 实验验证与分析

本文采用图8 所示的小型光伏组件搭建1×4的阵列。 光伏阵列朝南，间距为 0.3 m，倾角为30 °，组件面积为 551 mm×780 mm。 阵列东 1 m 处为一高 3.5 m、长 4 m 的釉面瓷砖墙面。 实验于2019 年 7 月 21 日、22 日针对高、中、低 3 种辐照情况进行，实测辐照度分别为 788，485，312 W/m2，其中中等辐照情况下设置了建筑物阴影遮挡，阴影遮挡面积为一个组件的1/4。 表1 为实验所采用的光伏组件电气参数。

图8 实验用光伏阵列Fig.8 PV array used in the experiments

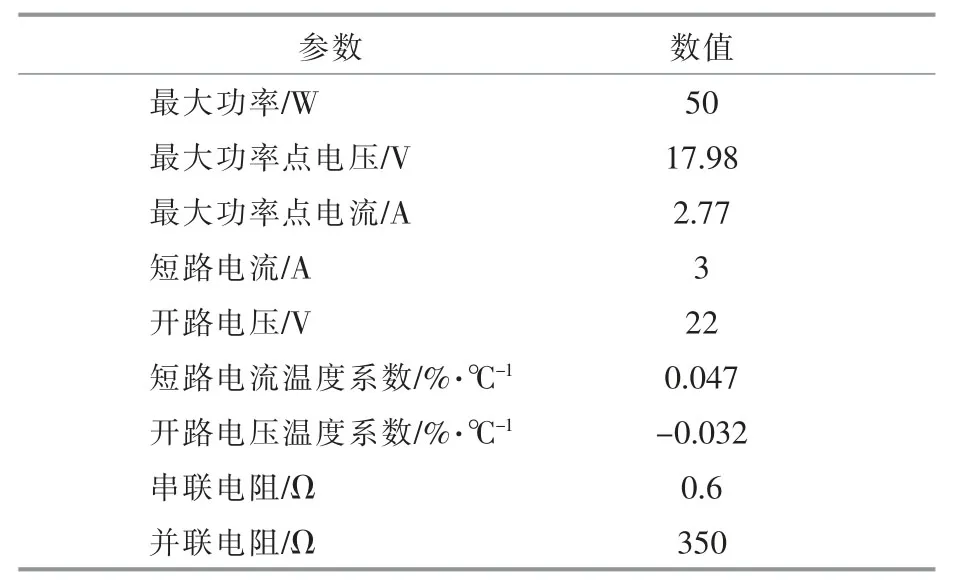
表1 光伏组件电气参数Table 1 PV module electrical parameters

表2 为通过本文建立的反射辐射模型的计算结果。 再将所求得的各辐照度代入光伏组件数学模型，叠加后得出计及反射辐射的光伏阵列I-V特性曲线（图 9），表3 为相应均方误差。 从表3 可看出，在屋顶光伏组件有周边建筑遮挡的情况下，计及反射辐射的模型相比未计及反射辐射模型更为准确，其原因在于阴影处受到来自建筑立面的反射辐射增强。 随着光伏阵列受到太阳辐照度逐渐降低，计及建筑立面反射辐射的模型精度也逐渐降低，其原因在于太阳辐照度较低时，所采用的直散分离模型准确度不高，导致直射辐射计算偏小，从而导致低辐照时模型输出比实际输出偏低。从建筑立面的反射辐射对光伏阵列的增益来看，低辐照下建筑立面对光伏阵列的功率增益最大，随着辐照度增大，功率增益逐渐降低，其原因在于低辐照下光伏阵列受到的建筑立面反射辐射占比远高于高辐照下。总的来说，对于屋顶分布式光伏阵列，计及反射辐射的分布式光伏阵列模型可更好地描述光伏阵列I-V 特性。

表2 辐射模型求解结果Table 2 Results of radiation model

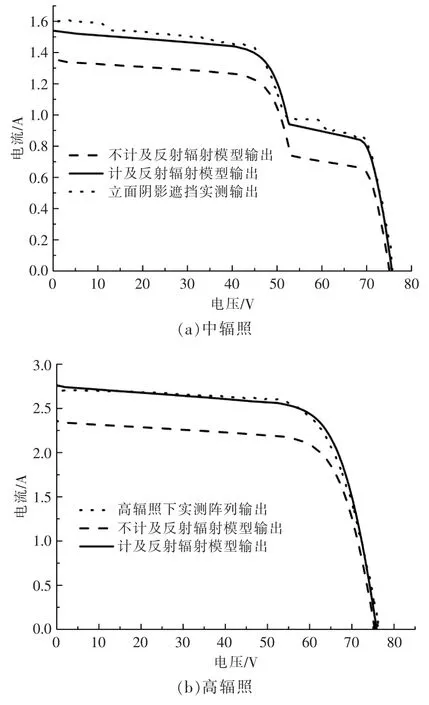
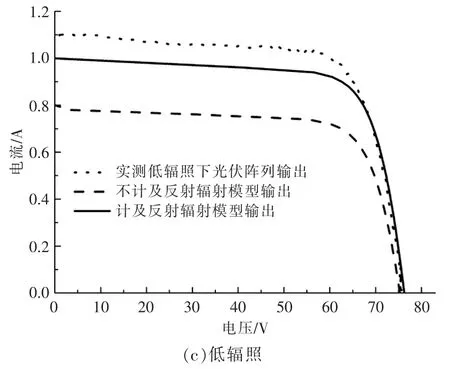
图9 中、高、低辐照下实测输出与计及、不计及反射辐射模型输出对比Fig.9 Comparison of measured output and calculation output model under medium, high and low irradiation

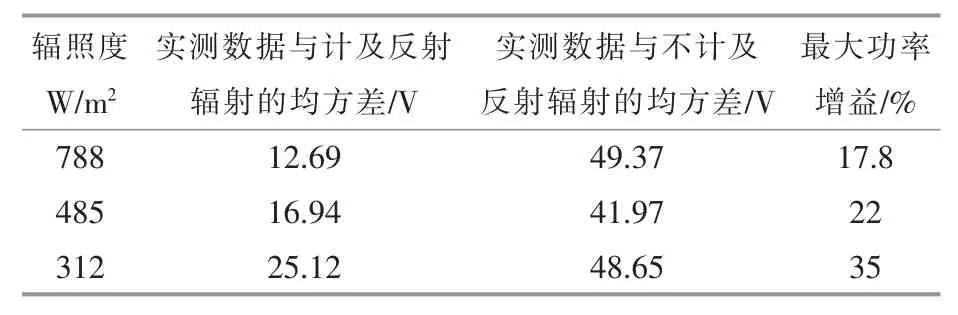
表3 不同辐照度下模型均方误差及最大功率增益Table 3 Root mean square error of model under different irradiances and gain of maximum power

3 总结

本文针对屋顶分布式光伏电站常规建模时未考虑建筑立面反射辐射对光伏阵列输出特性的影响，首先通过历史辐照度数据建立太阳光直散分离模型，在此基础上，结合太阳位置、建筑物立面材料性质等建立建筑立面反射辐射模型。 再结合组件安装形式、太阳位置、建筑物与光伏阵列距离等因素，最终建立计及反射辐射的分布式光伏阵列I-V 特性输出模型。 通过实验验证了反射辐射模型与所提出的计及反射辐射的分布式光伏阵列模型精度。 本文所提出的模型能够对屋顶分布式光伏电站的选址规划、运行维护提供参考。