计及微电网群合作博弈的主动配电网能量优化调度二层规划模型

格日勒图，张立辉，柴剑雪

（1.华北电力大学 经济与管理学院，北京 102206； 2.华北电力大学 新能源电力与低碳发展研究北京市重点实验室，北京 102206； 3.内蒙古电力（集团）有限责任公司，内蒙古 呼和浩特 010010）

0 引言

主动配电网 （Active Distribution Network，ADN） 可以实现分布式电源 （Distributed Energy Resource，DER）在配电网中广泛接入及高密度渗透[1]～[4]。 因此，分布式电源以微网群的形式接入主动配电网具有良好的发展前景[5]～[7]。

目前，已有文献对ADN 能量优化调度进行研究。 文献[8]计及储能和柔性负荷的时空联系以及网络潮流的影响，构建了多目标ADN 优化调度模型。 文献[9]建立了基于对代理系统的能量协调控制策略。 随着微网群技术成熟，对其能量优化调度成为热点，文献[10]针对含多微网主动配电系统分散自治的特点，提出一种基于目标级联分析理论的优化调度模型和求解方法。 文献[11]针对光伏微网MG（Mirco Grid）群提出一种基于合作博弈论的市场交易模型。以上文献在建立模型时，只是将ADN 作为一种已知的环境考虑，并没有考虑到ADN 的主动性。 目前很少有文献同时计及ADN 和MG 群两个利益主体的决策能动性。

本文首先介绍了含MG 群的ADN 基本结构和运行特性，其次采用二层规划模型对计及MG群合作博弈的ADN 能量优化调度问题进行建模。所建立的模型分别以ADN 运营商和MG 群联盟为上层决策者和下层决策者。 并给出了所建立二层规划模型的Stackelberg 均衡，作为求解流程设计的基础。 采用混沌粒子群算法设计模型的求解流程。 最后通过一个算例验证了本文所建立模型的合理性和有效性。

1 含微网群的ADN

在电力市场环境下，ADN 作为售电公司主体，具备系统内包括售电电价和购电电价在内的自主定价权，从而追求自身效益[12]～[14]。每个MG 中都接入了微燃机（Micro Turbine，MT）、风力发电（Wind Turbine，WT）、燃料电池（Fuel Cell，FC）、光伏发电 （Photovoltaic Cell，PV）、 储能（Storage Battery，SB）以及负荷（Load）。 当采用二层规划进行建模时，ADN 内各个决策者的决策依据和决策流程如图1 所示。

传统运行方式下，MG 群之间不存在合作博弈，ADN 直接与各个MG 进行市场交易和结算。当MG 群形成MG 群联盟之后，作为一个整体与ADN 交易与结算，并且在内部进行协调以分配合作剩余。上层决策者作为整个模型的领导者，其决策能够间接影响下层决策者的决策，从而影响自身的决策效果。 下层决策者通过反馈给上层决策者一定的指标从而影响上层决策目标。

图1 ADN 二层规划模型决策原理图Fig.1 The decision schematic diagram of bilevel programming model in active distribution network

2 上层模型

ADN 是上层决策者，决策变量为ADN 内各个微网或者MG 联盟之间一天内进行的购电电价曲线和售电电价曲线。 上层决策者的目标是最大化系统运行收益，其表达式为

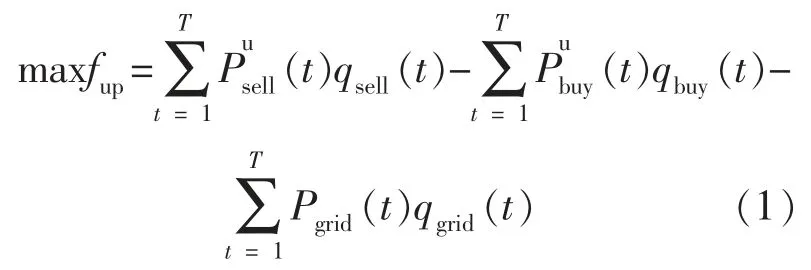
式中：fup为上层决策者的目标函数；T 为一天调度时段数分别为ADN 在 t 时段向MG 群联盟的售电功率和购电功率；qsell（t），qbuy（t）分别为ADN向MG 群联盟在t 时段的售电电价、购电电价；Pgrid（t）为 ADN 与外网在 t 时段的购售电功率；qgrid（t）为 ADN 与外网在 t 时段的购售电电价，大于零时表示购电。

为满足负荷用电需求，AND 须要确保系统内功率平衡，同时，AND 也要消纳MG 群中光伏、风电产生的剩余电量。 因此以及 P（t）是grid根据下层决策者MG 群联盟的决策而调整得到，并不是直接决定的变量，Pgrid（t）表达式为

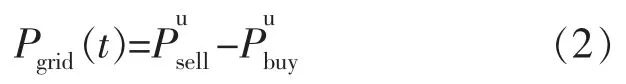
上层决策者需要满足的约束条件为

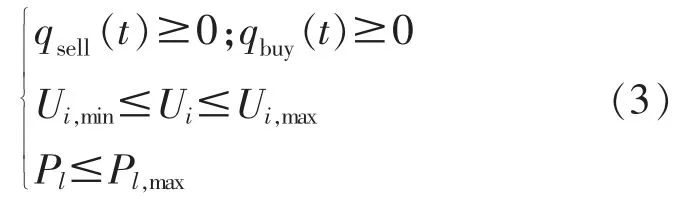
式中：Ui为 ADN 第 i 个节点的电压；Ui，min和 Ui，max分别为配电网第个i 节点电压的下限和上限；Pl为 ADN 第 l 条支路的有功功率；Pl，max为第 l 条支路的传输上限。

每个节点的电压为

式中：n 为 ADN 节点数；Pi，Qi分别为第 i 个节点流入的有功、 无功功率；Gij，Bij，δij分别为连接第 i个节点和第j 个节点线路的电导、电纳、电压相位差；Ui，Uj分别为第 i，j 个节点的电压值。

3 下层模型

博弈分为合作博弈和非合作博弈。 合作博弈即存在有约束力的合作协议的博弈，强调的是集体理性，注重公平与效率[14]，[15]。下层决策者为进行合作博弈的 MG 联盟，假设该联盟为 （N，ν），其中，N 为 MG 组成个数，ν 为联盟的合作剩余个数。联盟中每个MG 都遵守联盟的运行规则，每个MG 都需要制定自身的优化运行计划，而下层决策者MG 联盟的目标函数和约束条件也需要以该计划为基础。 因此本文下层模型首先建立MG 优化调度子模块，然后构建下层决策者的目标函数和约束条件。

3.1 MG优化调度子模块

在MG 联盟的决策中，每个MG 需要实现经济效益的最大化，但每个MG 受到该MG 内配置的分布式电源容量、储能容量、出力限值以及购售电功率限值的影响。

MG 优化调度子模块的目标函数C 为

式中：Cec，Cen分别为 MG 运行的经济成本、环境成本，其表达式为

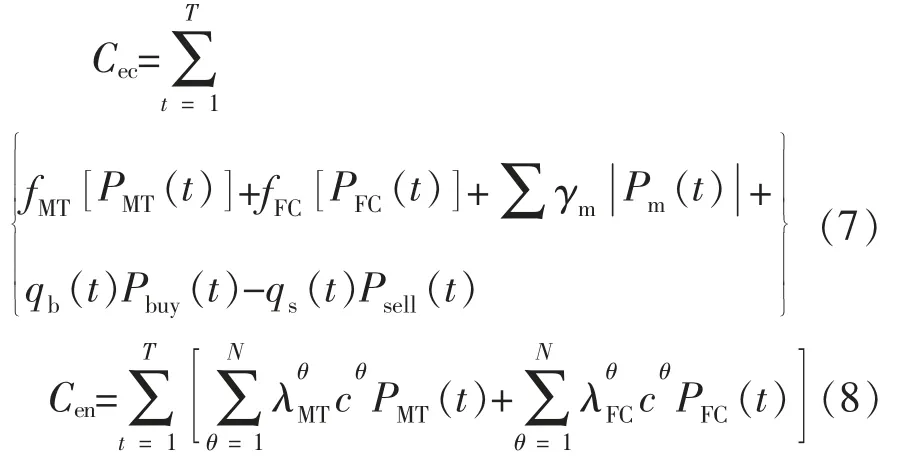
式中：fMT（）和 fFC分别为 MT 和 FC 的燃料成本函数，具体表达式参考文献[16]；PMT（t）为 t 时段 MT的计划出力；PFC（t）为 t 时段 FC 计划出力；γm为第m 台设备的运行维护成本系数；Pm（t）为t 时段第 m 台设备的出力；qb（t），qs（t）分别为 t 时段 MG与外界（ADN 或者 MG 联盟）的购、售电电价；Pbuy（t），Psell（t）分别为 t 时段 MG 与外界的购电功率和售电功率；θ 为污染物类别，共 N 种污染物为MT 第 θ 种污染物的排放系数为 FC 第 θ 种污染物排放系数；cθ为第θ 种污染物的单位排放量治理费用。

MG 优化调度子模块的约束条件为

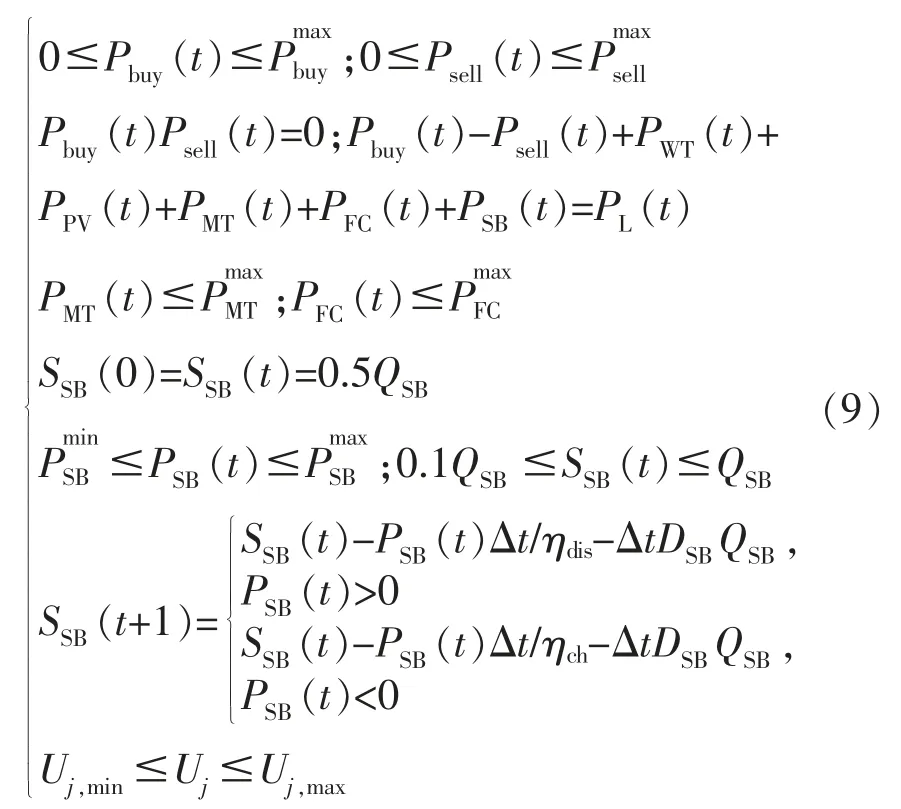
本文中各个MG 的运行成本主要收到外网电价水平的影响，当各个MG 不进行合作博弈时，有qb（t）=qbuv（t）和 qs（t）=qsell（t）。 当各个 MG 进行合作博弈时，有 qb（t）=qu（t）和 qs（t）=qu（t）。 qu（t）为 MG群联盟制定的内部一天交易电价曲线。 将第i 个MG 的运行成本看作是外网电价的函数，有其运行成本 Ci（qs，qb），其中，qs和 qb分别为变量售电电价曲线和购电电价曲线。

3.2 基于MG联盟合作博弈的下层模型

下层决策者的决策变量为MG 群联盟内部的一天交易电价曲线 qu（t），以及 MG 联盟与 ADN 的购售电功率曲线。 各个MG 在实际运行中由于配置不同，其具备的经济特性不同，也会产生不同的功率偏差，这种情况下，通过组成MG 联盟将其作为一个整体与ADN 进行交易，能够产生合作博弈剩余[17]，然后将这些合作剩余进行分配，使每个MG 的状况更好。

下层决策者的目标是最大化合作剩余，下层模型目标函数为

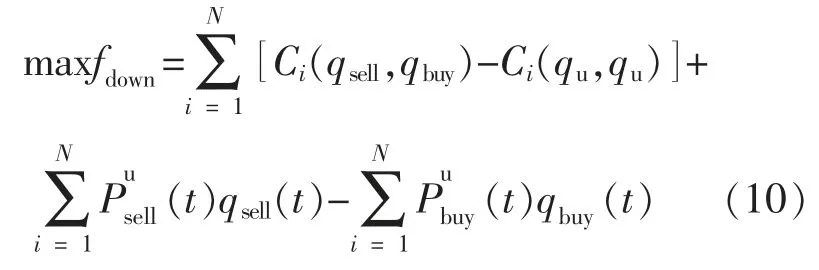
式中：fdown为下层决策者的目标函数；Ci（，）为 MG的运行成本，将该成本看作是购电电价曲线和售电电价曲线的函数，由MG 优化调度子模块得到。

下层决策者需要满足的约束条件如下。

①联盟内部电价曲线约束

②MG 合作收益不减约束

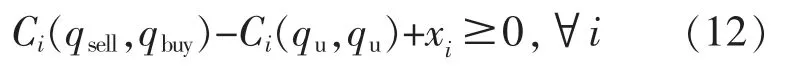
式中：Ci（qsell，qbuy）-Ci（qu，qu）为 MGi 在参与联盟前后节

省的综合运行成本；xi为MG 联盟向MGi 分配的合作剩余，采用Shapley 值计算后其值为[18]

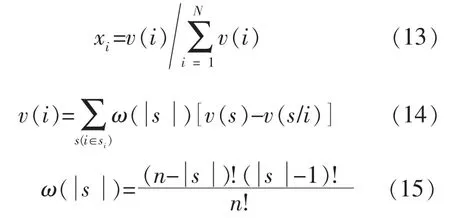
式中：si为联盟中包括MGi 的所有子联盟组成的子集为子集s 的元素数目为加权因子；v（s）为子联盟 s 的合作剩余；v（s/i）为子联盟除去MGi 后的合作剩余。

③购售电功率曲线约束

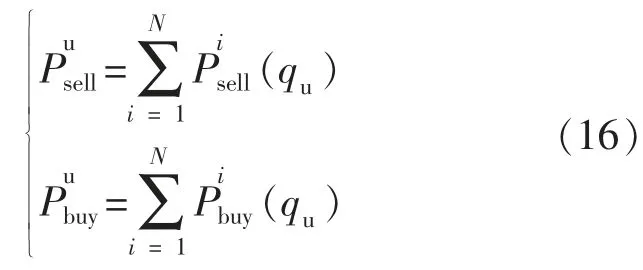
4 二层规划优化调度模型与Stackelberg均衡

4.1 二层规划综合模型

本文建立计及MG 群合作博弈的ADN 能量优化调度二层规划模型为

4.2 Stackelberg均衡

二层规划模型中上层决策者和下层决策者的决策相互影响，相互耦合，这使得其求解方法相比于一般的优化模型更加复杂[19]。 模型（18）的Stackelberg 均衡为当且仅当∀（qsell，qbuy），有：

本文对上层模型采用混沌粒子群算法进行求解，下层模型采用yalmip 优化工具箱进行求解[20]。在上层求解过程中，对下层求解过程进行调用，形成混合智能算法。

5 算例分析

5.1 算例设置

本文算例以IEEE 33 节点配电网系统为基础，构建了含微网群的ADN 模型如图2 所示。ADN 分别在节点 8，16 和 29 并网接入 3 个MG。

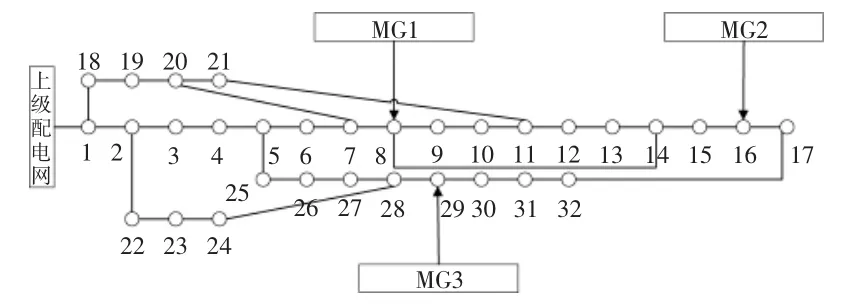
图2 IEEE 33 节点系统为基础的ADN 结构示意图Fig.2 Schematic diagram of the active distribution network based on IEEE 33 distribution system

ADN 与上级配电网或者输电网的功率交换采取分时电价机制，分时电价曲线参考文献[21]，微燃机和燃料电池的燃料成本函数、各个设备的运行维护成本系数、环境排放物折算系数参考文献[22]，[23]。 本文采用混沌粒子群设计建立模型的求解流程，其中混沌粒子群算法的参数如下：最大迭代次数为400，群体数量为60，两个学习系数均为 0.8，混沌搜索代数为 20。3 个 MG 内微源、储能配置情况以及负荷容量如表1 所示。

表1 ADN 内MG 配置情况Table 1 Configuration of microgrids in AND network

由于 ADN 地理范围有限，3 个 MG 的风、光出力曲线形状相同，而出力水平与装机容量有关，负荷水平特性存在差异，如图3 所示。

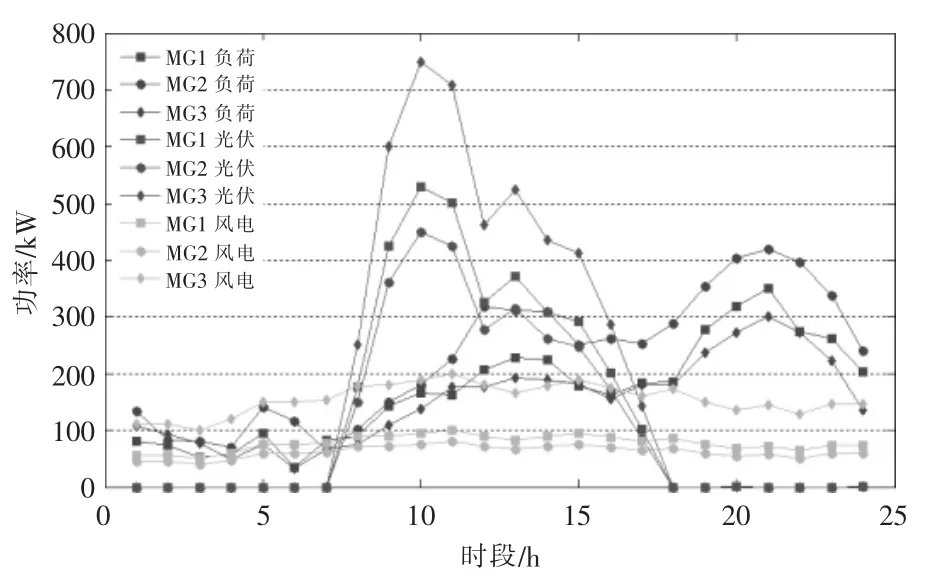
图3 各个MG 风电光伏出力和负荷水平Fig.3 Power curves of WT，PV and load level

为了比较不同情况下ADN 和MG 的优化运行情况，设置4 种方式：方式一为ADN 不具备自主定价权，MG 群不进行合作博弈；方式二为ADN不具备自主定价权，MG 群进行合作博弈；方式三为ADN 具备自主定价权，MG 群不进行合作博弈； 方式四为ADN 具备自主定价权，MG 群进行合作博弈，也即本文模型针对的情况。

5.2 仿真结果

以运行方式四为例，ADN 制定的与MG 联盟之间的电价曲线如图4 所示。

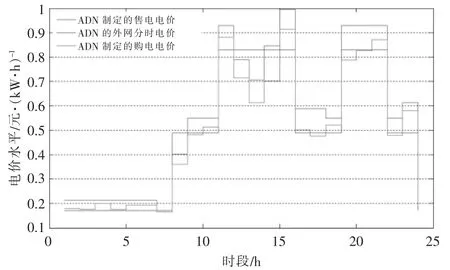
图4 ADN 制定的与MG 联盟电价曲线Fig.4 Electricity price curve established with microgrid alliance by active distribution network

在上层决策者做出的决策下，MG 联盟中每个MG 的优化运行方案分别如图5～7 所示。

图5 MG1 系统优化运行方案Fig.5 Optimization operation scheme of MG1 system

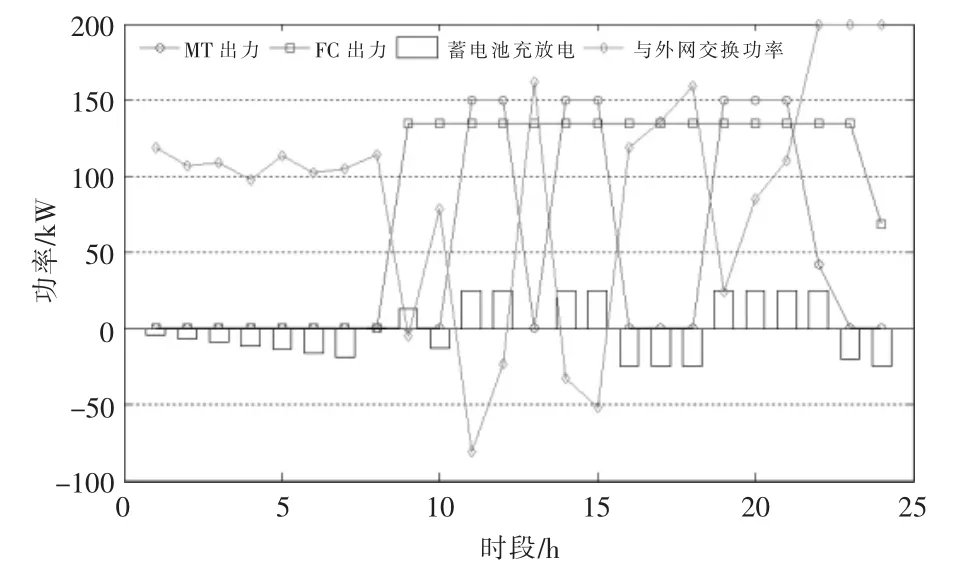
图6 MG2 系统优化运行方案Fig.6 Optimization operation scheme of MG2 system

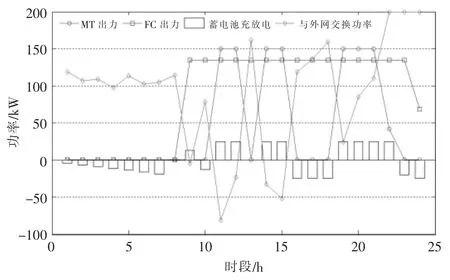
图7 MG3 系统优化运行方案Fig.7 Optimization operation scheme of MG3 system

由图5～7 可以看出，MG1 在第1～7 时段内，系统处于谷时段，基本采用联盟内低价的电能进行供电，储能充分充电，为之后获取削峰填谷效益做好准备。然而由于储能容量有限，储能并没有按照额定功率进行充电，同时MG1 中储能的作用主要是功率平抑作用而且成本较高，不宜配置过大容量。 在第8～16 时段，分布式光伏出力达到高峰，MG 联盟内部交易电价以及联盟和ADN 之间的交换功率电价均较高，MG1 充分向联盟售电以获取收益。在之后的时段，系统迎来了负荷高峰时段，不仅储能充分放电，FC 满发，连成本相对较高的MT 处于开机状态，以满足紧张的功率需求。

在每个MG 制定自身优化运行方案的基础上，模型还得到了4 种运行方式下ADN 和MG 群运行指标对比，如表2 所示，其中各项成本均指一天的运行成本，当成本为负时，表示实际上存在收益。 由表2 可知：在方式一下，ADN 与 MG 进行传统方式的能量交易，ADN 并不能作为供电公司主体拥有定价权，而MG 之间也不进行合作博弈，此时系统运行各项指标均为一般状态； 方式二中，MG 联盟进行了合作博弈，导致MG 联盟内各个MG 的多种成本指标均小于方式一，与方式一相比，ADN 的收益显著下降，这说明MG 联盟的合作博弈获取了合作剩余； 方式三中，ADN 具备了自主定价权，增加了ADN 的运行收益，但也增加了MG 的负担，在实际中方式三是最不可取的运行方式，因为这是一种垄断现象；方式四中MG 联盟存在合作剩余，但已经小于方式二，MG 联盟运行成本上升，ADN 作为决策者也具备了一定的主动性，挽回了一定的效益损失。

表2 4 种方式下系统运行参数比较Table 2 Comparison of system operating parameters under four modes 元

6 结论

本文首先针对ADN 作为售电主体具备自主定价权，同时含MG 群进行合作博弈的问题背景，采用二层规划理论对ADN 和MG 联盟的优化运行模型进行建模，所建立模型充分考虑了模型中多决策主体和分层决策的特性。 通过分析二层规划模型的Stackelberg 均衡作为对模型求解的基础。 仿真结果表明，ADN 的自主定价权和MG 群合作博弈都是各自追求运行效益和降低运行成本的手段，当MG 群组成合作博弈联盟时，ADN通过自主定价权能够追求自身效益，与MG 联盟形成制衡，有利于合理分配的系统运行社会经济效益，促进各方决策者的市场主动性。