改进的Knothe时间函数开采沉陷动态预计模型研究*

陈卫卫

（安徽理工大学测绘学院， 安徽 淮南 232001）

研究开采沉陷动态预计的精确方法， 不仅可以为 “三下” 采煤的方法提供理论依据， 而且可以实时评测采动影响区域的岩层移动情况， 对建 （构）筑物的维修与加固方案提供指导意见[1]。 开采沉陷动态预计过程可以表述为岩层移动公式与时间函数的结合， 反映不同时刻的岩层移动规律。 目前常用的时间函数模型为Knothe 时间函数模型， 针对Knothe 时间函数模型与实际岩层移动过程的不符性， 许多专家提出了建设性意见。 如文献[2]增加了监测点下沉曲线上的观测期数及达到最大速度所需时间的幂指数参数； 文献[3]用分段建模的方法建立改进的Knothe 时间函数模型， 但该模型表明地表下沉过程对称于下沉总时间的一半， 与实际情形不太符合； 还有学者利用岩石非定常流参数改进Knothe 时间函数。 这些方法虽在一定程度上修正了Knothe 时间函数的不足， 但仍存在一定局限性。

为反映岩层移动动态过程的时空非线性特征，本文增加了影响时间变化的幂指数参数和反映岩层移动非线性特征的参数， 构成一个三参数的时间函数模型[4]。 结合工程实例验证， 该模型能够较好地反映开采沉陷下沉过程的客观规律。

1 三参数Knothe时间函数模型的建立

1.1 改进的Knothe时间函数

Knothe 时间函数模型为

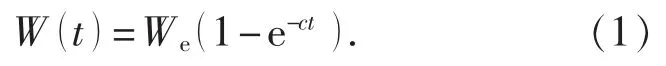
式中： W(t )为地表下沉量； We为地表稳沉后某监测点的最大下沉值； c 为覆岩岩性参数， 其值与上覆岩层的力学性质密切相关； t 为地表自回采时起的下沉时间。

为了使Knothe 时间函数模型描述的下沉过程符合岩层移动 “稳定—变化—稳定” 的动态演化客观规律， 本文采用三参数的Knothe 时间函数模型， 即

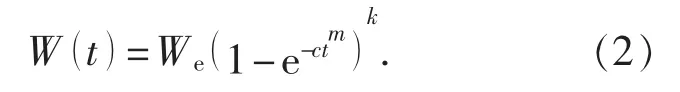
式中： c 为初始沉降速度参数； m 为时间幂指数参数； k 为曲线形状参数。

1.2 合理性论证

当 m=1， k=1 时， 式 （2） 可转化为式 （1）。其中， 式 （2） 对t 求一阶导数和二阶导数， 分别可得到下沉速度和下沉加速度， 计算公式为

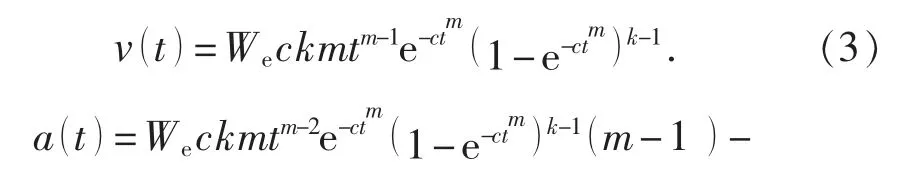
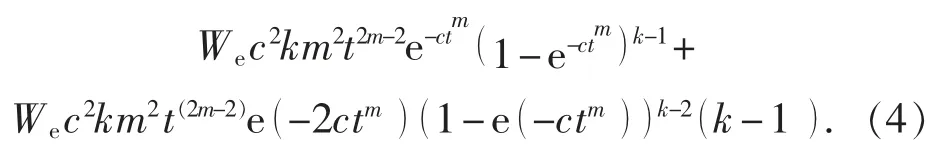
本文以最大下沉点 （ML01） 为例， 分别绘制式 （2） ～式 （4） 的下沉曲线、 下沉速度曲线和下沉加速度曲线的图像， 见图1～图3。

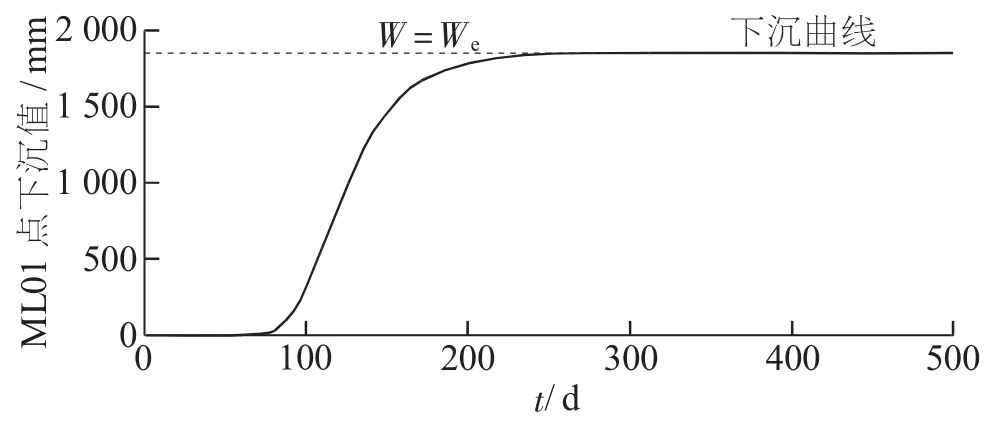
图1 ML01 点的下沉曲线

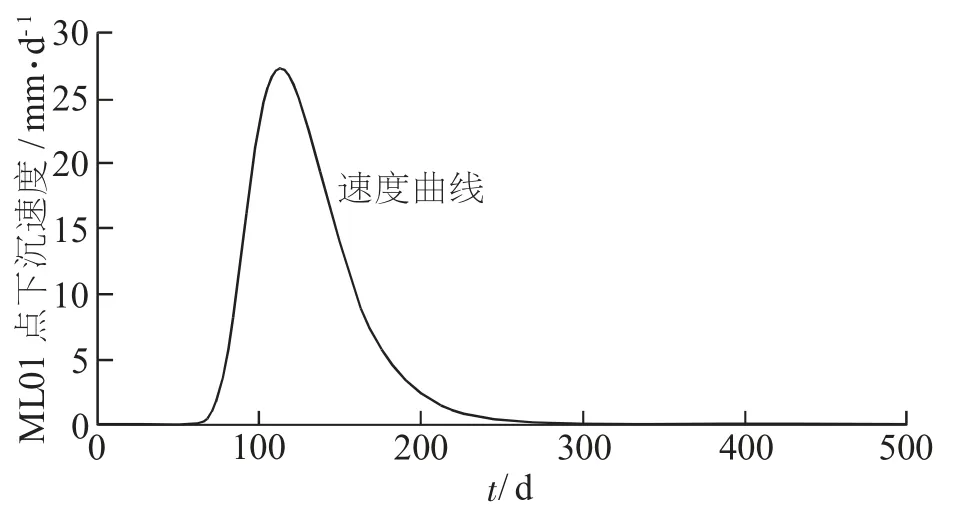
图2 ML01 点的下沉速度曲线

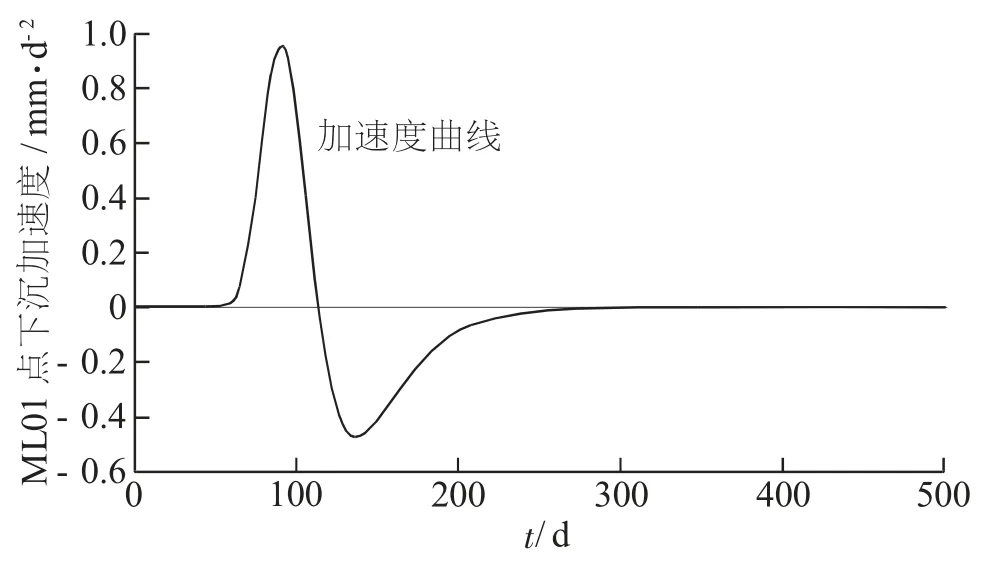
图3 ML01 点的下沉加速度曲线

由图1 可以知道， 当 t=0 时， W(0 )=0； 当t→∞ 时， W(∞ )=We， 这说明修正后的 Knothe 时间函数经过原点， 且存在上限值， 其值为所预测点稳沉后的下沉值。 由图2 可以知道， 下沉速度v 是随着时间而先增加后减小的。 由图3 可以知道， 当下沉加速度a＞0 时， 下沉速度v 逐渐增大； 当下沉加速度a 第二次等于0 时， 下沉速度v 达到最大， 约为 27.28 mm/d； 当下沉加速度 a＜0 时， 下沉速度v 逐渐减小， 直至为0。 将改进的Knothe 时间函数与式 （1） 比较可知， 本文建立的模型符合实际地表点的下沉量和下沉速度的变化情况。

2 基于遗传算法的Knothe时间函数参数求解

2.1 遗传算法原理

遗传算法是一种模拟物种繁衍过程的优化算法。 许多物种在进化过程中， 遵循适者生存、 优胜劣汰的法则， 通过自身变异不断增强适应环境的能力， 其中一部分物种因无法适应环境的改变而被淘汰， 而另一部分适应环境的物种则被保留下来， 这个过程即为生物的进化。 将生物进化的3 个机制（选择、 交叉和变异） 运用到遗传算法的参数寻优中， 可以有效地迭代出最优解。

遗传算法的参数寻优过程可简单描述如下。

1） 设置迭代次数、 最大进化代数， 并进行种群初始化[5]。

2） 模拟个体在自然环境下的生存机制[6]， 构造适应度函数 （目标函数）。

3） 对种群个体进行选择、 交叉和变异操作[7]。

4） 设置终止迭代的条件， 不断重复步骤2 和步骤3， 直至达到收敛精度后， 停止迭代， 目标函数的最优解即为适应度最高的个体[8]。

为了更加详细地反映遗传算法求参的迭代过程， 设计遗传算法流程图， 见图4。

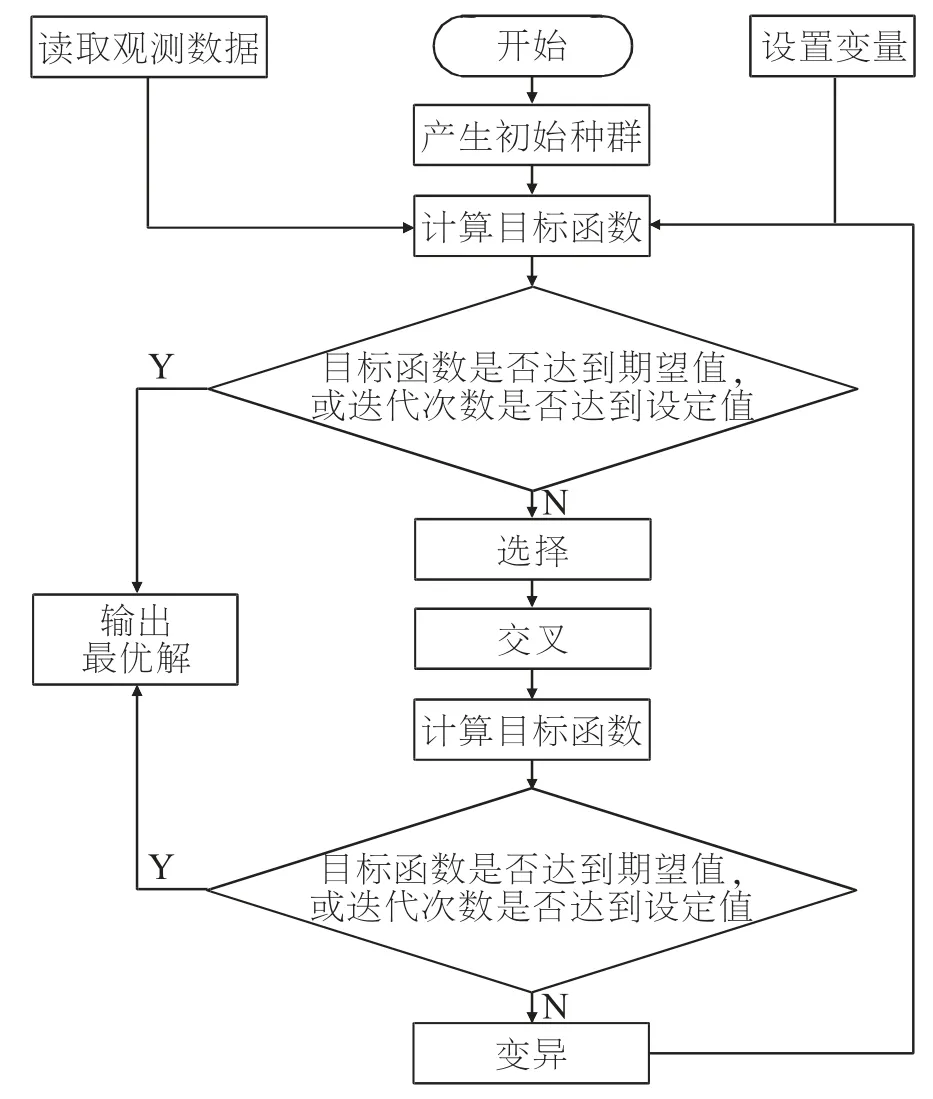
图4 遗传算法流程图

2.2 模型精度评价方法

依据最小二乘原理构造遗传算法的适应度函数（目标函数）， 该函数表达式为

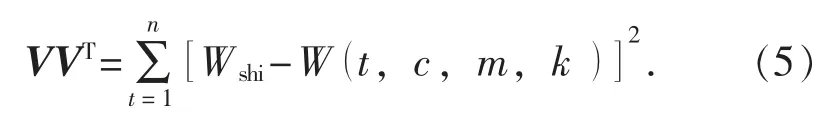
式中： Wshi为某点在各个时间段的真实下沉量组成的向量， mm； W (t， c， m，k )为某点在各个时间段的预计下沉量组成的向量， mm。

考虑到观测时间期数有限， 本文采用三次样条插值法对观测数据进行等间距插值。 同时为了验证Knothe时间函数模型的可靠性， 采用中误差评定模型精度， 其表达式为

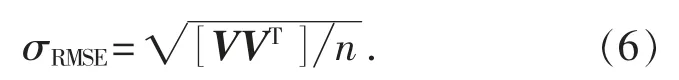
式中： n 为实验过程中通过插值的下沉值个数。

3 改进的开采沉陷预计模型的应用实例

根据安徽淮南某矿1613 （1） 工作面地表移动观测站实测资料和地质采矿条件可知， 1613 （1）工作面地表移动观测站布设成半条走向观测线和一条全倾向观测线。 工作面走向长约为1 528 m， 倾向长约为251 m， 开采时间为275 d， 顶板管理方式为全部垮落法。 该工作面平均采厚为2.9 m， 煤层倾角为3°， 为近水平煤层。 根据井上下对照资料可知， 回采工作面的平均埋深约为668 m， 新生界松散层厚度约为420 m。 该工作面于2017 年3月 26 日开始回采， 到 2017 年 12 月 25 日刷面结束， 最后一次全面观测于2019 年1 月中旬完成。

采用MATLAB 软件平台编写遗传算法求参程序[9]， 得出所求参数值分别为 c=0.071 4； m=0.9；k=159.5。 将所求参数代入式 （2）， 得出预计最大下沉点 （ML01） 在各个观测时期的拟合下沉值，并与实测下沉值进行对比， 见图5。

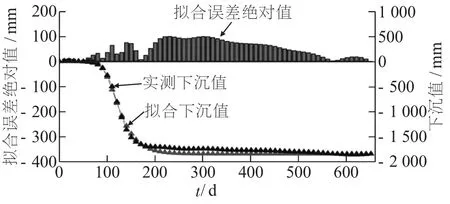
图5 ML01 点拟合下沉测值与实测下沉值的对比

以中误差为模型精度评价指标， 对Knothe 时间函数模型进行精度评定。 由图5 可知， 1613 （1）工作面的最大下沉点 （ML01） 在动态过程的拟合曲线总体上效果较好， 最大下沉点的拟合中误差为59.45 mm； 初始期、 活跃期误差较小， 能够准确地描述初始期、 活跃期下沉客观规律； 衰退期最大误差达100 mm， 衰退期误差较大可归因于淮南矿区厚松散层沉陷盆地下沉收敛速度慢。

4 结论

1） 对淮南某矿 1613 （1） 工作面地表移动观测站实测资料研究得出： 遗传算法求解动态下沉预计方程参数， 能较精确地描述最大下沉点的实际下沉规律； 动态预计方程总体拟合中误差为59.45 mm，研究结果可为矿区沉陷监测提供新方法、 新思路。

2） 应用三参数Knothe 时间函数模型对淮南某矿最大下沉点实现动态下沉预计， 结果表明改进的Knothe 时间函数模型对该点不同观测时期的动态预计有较好精度和可靠性； 研究结果能更客观真实反映岩层下沉量、 下沉速度随时间的客观变化规律。