沉管隧道变截面管段浮运与沉放水动力特性及方案评价

熊正元, 杨春山, 陈凌伟

(1.广州市市政工程设计研究总院有限公司, 广东 广州 510060; 2.华南理工大学 土木与交通学院,广东 广州 510641)

沉管隧道具有诸多的优点[1-3],在越江跨海通道中得到了越来越多的应用,但在其建设过程中各种问题也日益显现,相关研究成果涉及沉管隧道结构受力[4-5]、地基处理[6-7]及地震响应[8-9]。由于沉管隧道建设在我国尚属起步阶段,对于沉管隧道建设中关键问题的研究还远远不够,如变截面沉管管段浮运沉放水动力特性仍未取得合理认识。变截面管段与常规等截面管段相比,在预制、承载、浮运、沉放及对接等过程均存在较大的难度和风险。

数值模拟、试验观测及理论分析是水流流动问题研究的常用方法。其中物理模型试验成本高且难以分析耗能内流机理,理论分析则需对计算介质进行抽象和简化,且给出解析解较困难;相比之下,数值模拟能形象而细致地再现水流的复杂流动,研究方法灵活、周期短、费用低,且便于揭示水流流动机理。因此,本文以洲头咀沉管隧道变截面管段为研究对象,借助计算流体动力学(computational fluid dynamics,CFD)软件开展变截面管段浮运和沉放过程流体绕流模拟,并通过模型试验验证,揭示变截面管段浮运与沉放过程绕流流场、压力场及涡动结构演化特征,最后,对变截面管段浮运与沉放过程牵引系泊方案开展评价与优化。

1 工程概况

广州市洲头咀隧道西连芳村的花蕾路,穿越珠江后东连海珠区内环路的洪德路立交,隧道穿越珠江段340 m采用沉管法,分成E1、E2、E3及E4共4节,沉管管段总体设计如图1所示(单位为m)。由于两端立交距离珠江堤岸较近,与其相接的内环预留匝道较高,为了保持较好的行车条件,满足接线减速与渐变段标准的要求,沉管段和岸上段衔接的管段E1与E4采用了变截面管段,本文以E1管段为分析对象。

E1管段沿纵向特性渐变,使其浮运与沉放阶段存在纵向倾覆失稳的风险,因此有必要制定相应的控制措施以防止管段纵倾。通过计算得到E1管段纵向倾覆力矩为111 116.05 kN·m,结合隧道建设特点,在变截面管段内局部设置面积为156.53 m2、厚度为1.15 m、体积为180.54 m3、重度为23.5 kN/m3的素混凝土压重层。

图1 沉管管段总体设计方案

2 管段浮运、沉放CFD模拟

2.1 计算模型的建立

由于变截面管段浮运与沉放是在设计控制条件下完成的,实际实施过程中需要控制复杂水流形态的出现,本文将水流流体视为简单流体,用Navier-Stokes方程来描述[10-11],且用k-ω湍流模型。变截面管段浮运与沉放座底三维计算模型如图2所示(单位为m),模型中水域采用不可压缩黏性流体单元模拟,计算区域在X、Y方向分别取95.00、165.00 m,Z方向浮运阶段取22.00 m、沉放阶段取10.41 m。为了消除流体计算数值扩散的影响,模型均采用六面体单元。

CFD模型入流边界设定水平均匀流速,出流边界在未受扰动远场设压力,管段轮廓定义为无滑移壁面,计算域初始场用入流速度条件初始化。通过现场实测,管段浮运、沉放阶段相对流速分别为0.467、0.890 m/s,干舷高度为15 cm,水流动力黏度为1 MPa·s,密度为1 t/m3。CFD绕流变截面管段计算共200步,每间隔5步输出计算结果,每步时间增量0.1 s,最大迭代步数为20步,结果分析从100步开始(10 s),至计算结束(20 s)。

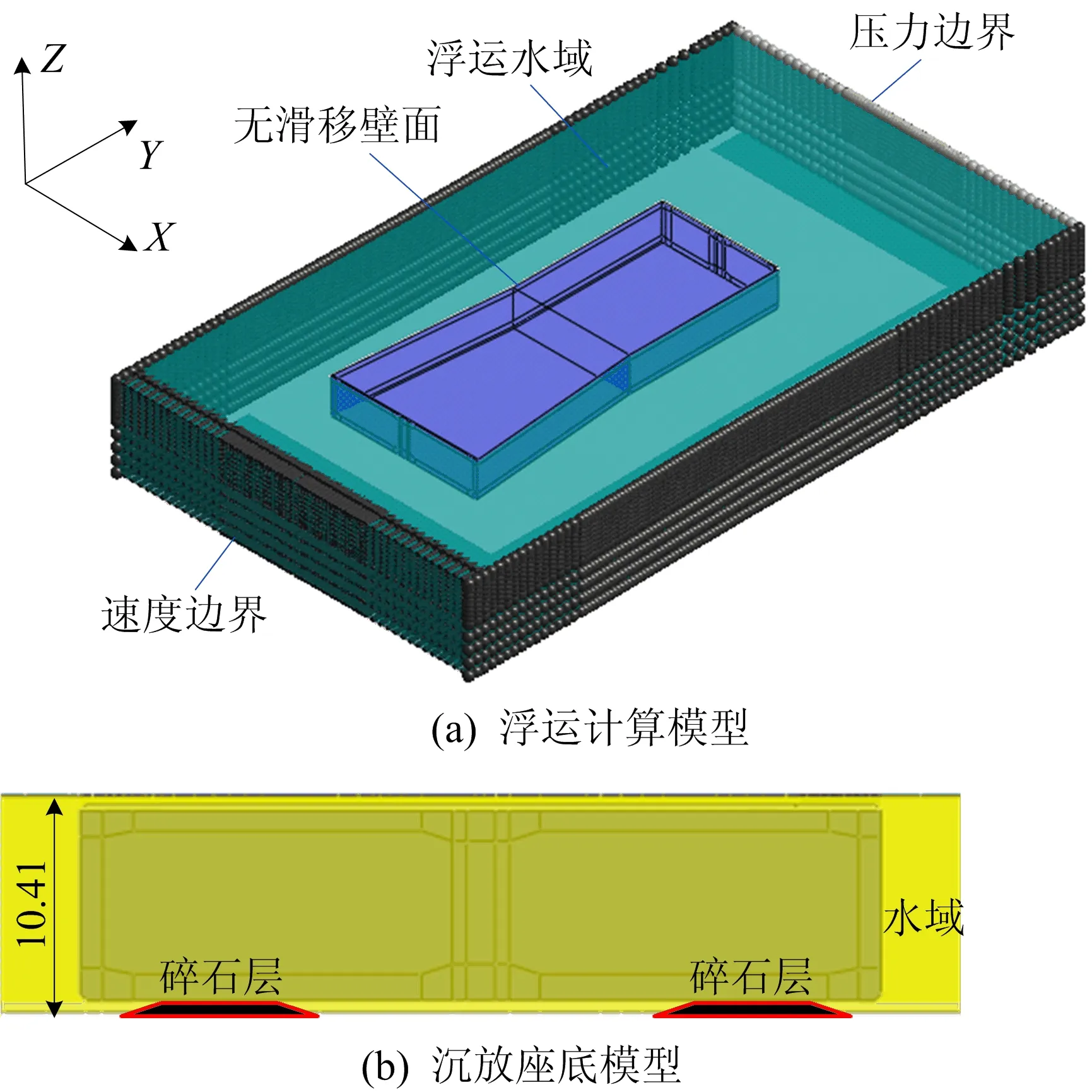
图2 管段浮运沉放CFD模型

2.2 模型可靠性验证

变截面管段浮运方案确定前期开展了模型试验[12],试验方案如图3所示(单位为m)。试验水池长200 m,宽6 m,设定了0.40、0.55、0.65 m共3个水深,试验几何相似比为1∶30,流速相似比为1∶5.48,试验探讨了不同流速对应的管段水流力。

为了验证变截面沉管管段浮运与沉放流体动力学三维计算模型的可靠性,采用CFD计算模型计算不同流速对应的水流力,并与模型试验结果对比分析。

变截面管段浮运与沉放座底设计流速对应的最大水流阻力云图如图4所示。从图4可以看出,变截面管段浮运和沉放座底迎水面受到的最大水流阻力分别为0.282、0.942 kPa。以相同的方法设定流速为设计流速(0.467 m/s)的1.00、1.32、1.64、1.96、2.26倍(实测最大相对流速为1.057 m/s),计算得到不同流速浮运时管段受到的水流阻力,其与试验结果对比如图5所示。

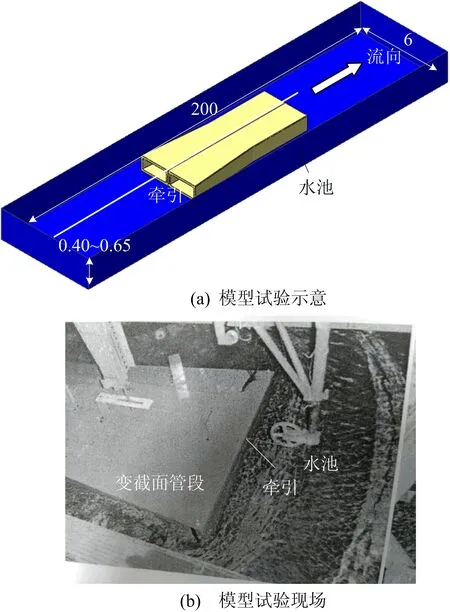
图3 管段浮运模型试验

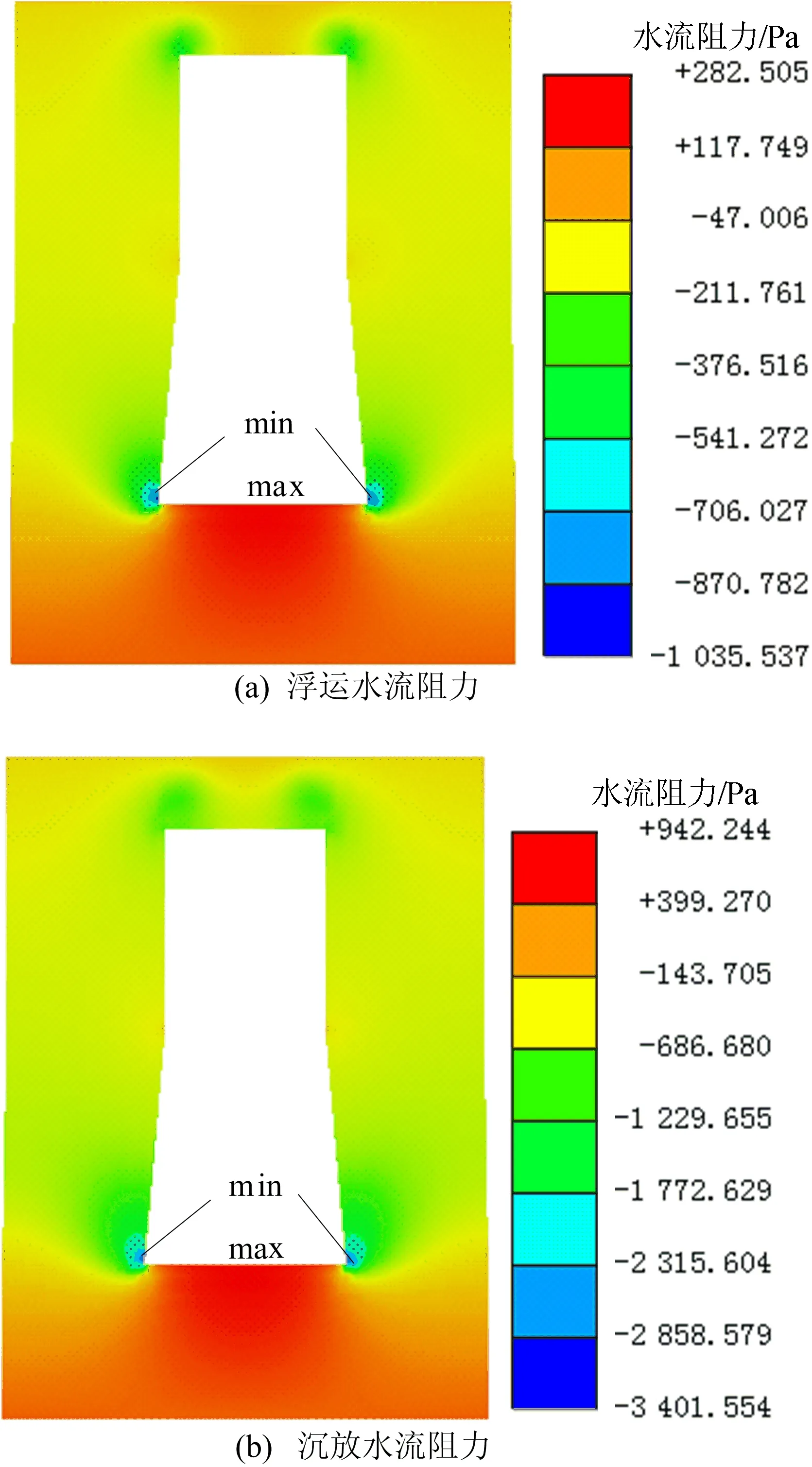
图4 管段浮运与沉放过程水流阻力

由图5可知,数值计算结果反映了变截面管段浮运阶段水流阻力的发展趋势,与模型试验所得结果较为吻合,说明本文采用的CFD计算模型具备可靠性。数值计算水流阻力总体比试验结果略大,这是由于数值计算考虑的吃水深度略大于模型试验,且流体参数也稍有差异。

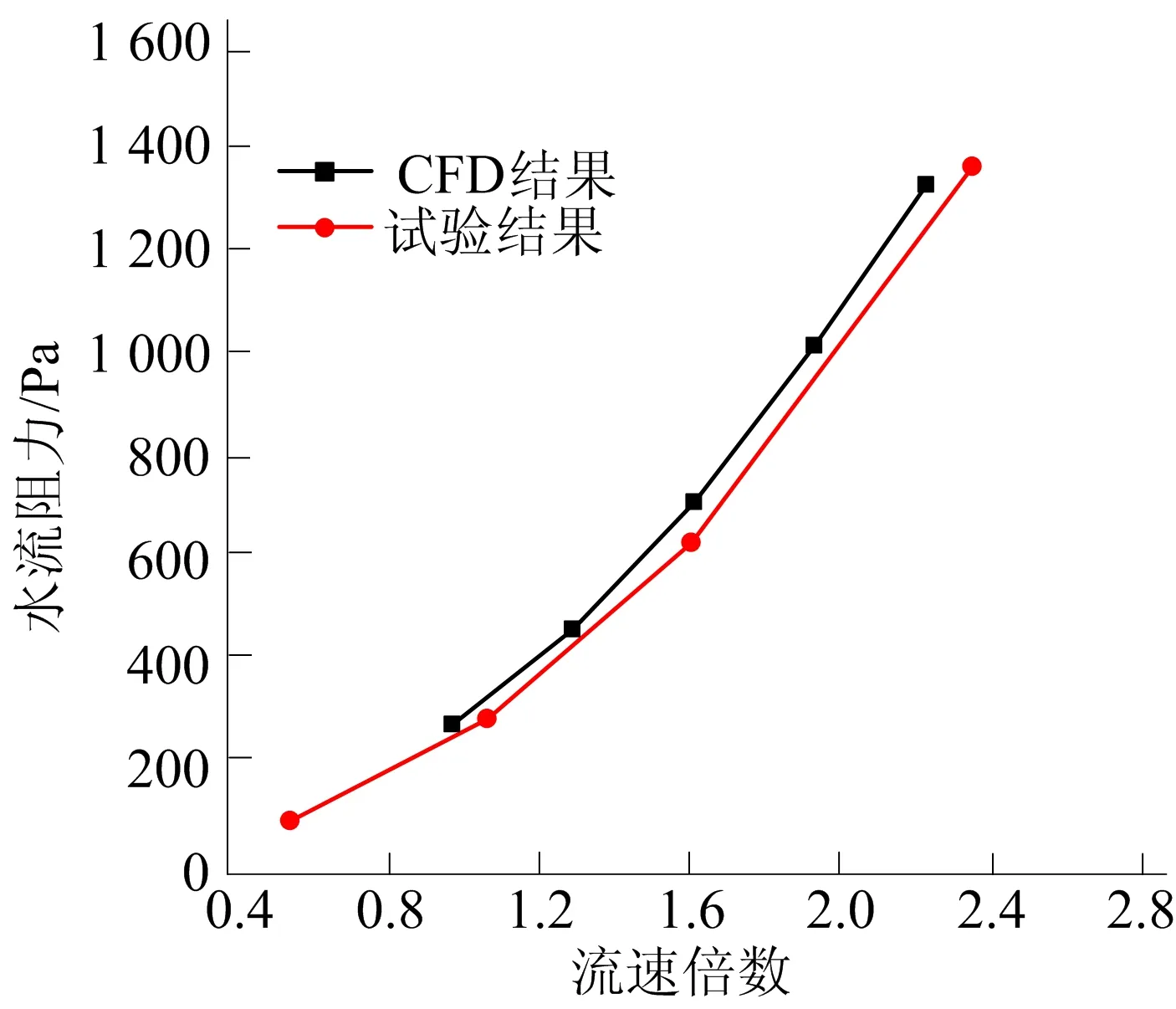
图5 水流阻力数值与试验结果对比

2.3 水动力特性分析

变截面管段浮运与沉放座底水流流场云图,如图6所示。

图6 浮运与沉放过程水流最大流速云图

由图6可知,初始速度为0.467 m/s的水流因管段钝体的存在,水流绕流管段加速减压,产生的最大流速为1.340 m/s;初始速度为0.890 m/s的水流引起的最大流速为2.999 m/s。

管段浮运与沉放局部水流流场如图7所示。从图7可以看出,在管段结构边界层处,在壁面的黏滞阻力和逆压梯度作用下,来流被挤向主流区,使水流与壁面边界层分离,且管段尾部流态结构会发生明显变化,形成一定尺度的回流区。

图7 管段浮运与沉放局部水流流场

从图7还可以看出,水流质点在管段侧墙处受壁面摩阻的影响,流动速度较小,而在管段迎水面与背水面转角处水流经历了加速减压的过程,因此流速明显增大。管段浮运涡动演化过程如图8所示。

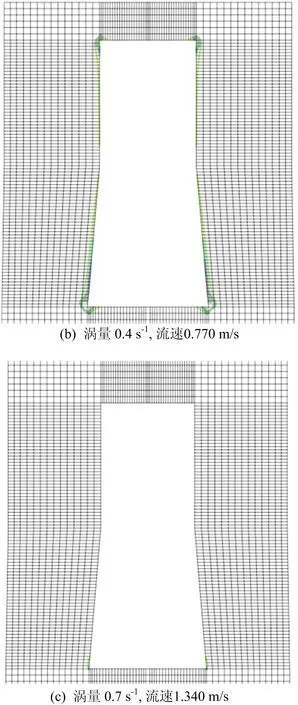
图8 涡量与对应的流速等值线

从图8可以看出,因管段壁面的存在,水流条件不平顺,局部出现了湍动,形成不规则流动,出现了特征紊流,并在侧壁周围形成旋涡现象。

由浮运与沉放CFD计算结果,得到变截面管段浮运与沉放座底旋涡强度随水流流速的变化规律如图9所示。

图9 涡量与流速关系

由图9可知,随着水流速度的增加,旋涡的涡量近线性增大,说明涡动强度呈现逐渐增强的趋势。

3 管段浮运与沉放方案评价

洲头咀沉管隧道管段浮运与沉放过程未使用拖轮,而是在工程船舶、地锚及重力锚定位后布置卷扬机及牵引点,用钢缆绞拖牵引的方式浮运与沉放锚固。管段浮运阶段钢缆与管段的夹角θ在变化过程中均大于或等于40°,结合CFD计算结果,得到管段浮运过程受到的水流力为Fw1=105.77 kN,则牵引钢缆受到的力N1为:

N1=0.5Fw1/cosθ

(1)

考虑到实际施工中夹角θ小于90°,该角度范围内余弦函数单调递减,因此(1)式计算结果极大值对应角度为40°,由此计算得到钢缆拉力为69.04 kN,远小于φ28 mm钢缆破断荷载460 kN,浮运牵引方案可满足强度要求。

管段临时系泊锚定初始方案如图10所示。

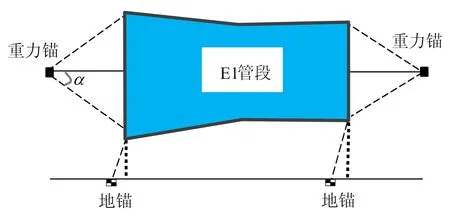
图10 管段临时系泊锚定初始方案

管段沉放系泊采用170 t的水中重力锚系泊锚固,重力锚采用φ42 mm钢丝缆系泊,破断荷载为980 kN。岸上地锚尺寸长、宽、高分别为2.5、1.6、1.7 m,设计的锚固力为150 kN。数值计算得到管段沉放座底受到的水流力为：

Fw2=0.942 kPa×375.1 m2=353.34 kN。

重力锚受力示意图如图11所示(单位为m)。

图11 重力锚受力示意图

图11中缆桩为结构系钢缆构件,α为管段钢缆水平面投影与水流方向夹角,β为管段钢缆与垂直面的夹角,自重G=1 800 kN,由设计方案可知α=19°,β=78°。根据力的平衡可知，重力锚钢丝缆受到的拉力N2满足:

Fw2=2N2cosαsinβ

(2)

由 (2) 式计算得到重力锚单根钢丝缆承受的拉力N2=191.05 kN,明显小于钢丝缆的破断荷载1 750 kN,并且由钢缆引起重力锚的倾覆力矩为1 528.43 kN·m,远小于自重提供的抗倾覆力矩7 200 kN·m,因此管段沉放系泊满足强度和稳定性要求。根据计算结果,从技术经济性出发可对管段牵引系泊钢缆方案作优化,牵引钢缆取直径φ24 mm,系泊钢缆取直径φ32 mm。

基于朗肯土压力理论[13],计算得到地锚受到的被动土压力为160.82 kN,锚块与周边土界面摩擦系数为0.3,从而得到锚块所受摩擦力为160.82 kN×0.3=46.92 kN。根据地锚的尺寸和重度25 kN/m3,计算其重力为170 kN,由此计算得到岸上地锚具有的锚固力为46.92 kN+170 kN=216.92 kN,大于150 kN的设计锚固力,满足稳定性要求。

4 结 论

(1) CFD分析结果与模型试验结果吻合,借助数值法模拟管段浮运与沉放力学特性合理可行;管段浮运与沉放座底,水流绕流管段且加速减压,最大流速分别为1.340、2.999 m/s。

(2) 管段迎水面来流被挤向主流区,使水流与壁面边界层分离,在尾部形成回流区。管段表面局部出现了紊流,并在侧壁周围形成旋涡,涡动强度随水流流速的增加而逐渐增强。

(3) 变截面管段浮运牵引与沉放系泊的钢缆作用力显著小于钢缆破断荷载,说明管段浮运与沉放钢缆设置方案满足强度要求。

(4) 变截面管段沉放座底系泊采用的重力锚和地锚可满足稳定性要求;根据计算分析,对管段浮运与沉放钢缆的方案作了优化。

沉管隧道建设发展迅速,其实施条件也越来越严格,为满足隧道与两岸路网的良好衔接,变截面沉管隧道必将得到更多应用。CFD模拟计算可描述实际变截面管段浮运与沉放的水动力特性,针对变截面管段水中作业表征出的动态力学特征,建议开展必要的流体动力学分析,从而制定切实可靠的实施方案。