求解仓储作业优化问题的多物种协同进化算法
杨文强, 张素君, 郭 昊
(河南科技学院 机电学院,河南 新乡 453003)
0 引言
大型电商平台进一步拓展了自动化立体仓储的应用领域,对自动化立体仓储技术来讲既是机遇又是挑战。仓储作业是仓储业务中最耗时的,大约占到仓储业务总耗时的55%[1],因此优化仓储作业效率就显得至关重要。截至目前,国内外学者在这方面已经开展了一些研究工作。Henn等[2]和Tsai等[3]基于禁忌搜索算法对传统仓储订单批量拣选优化问题进行了研究;Bottani等[4]考虑到货位分配策略也是影响仓储拣选效率的一个关键因素,采用遗传算法对货位分配优化问题进行求解,使拣选路径缩短20%左右;De Santis等[5]以最小化订单拣选距离为优化目标,提出了基于蚁群算法及弗洛伊德算法的混合型元启发式算法;Theys等[6]和Ascheuer等[7]将仓储订单拣选优化问题等效为经典的TSP(travelling salesman problem)问题进行求解;Lu等[8]考虑到订单到达时间有一定的随机性,认为仓储系统应具有一定的柔性,基于干涉路由选择算法对动态订单拣选优化问题进行了分析研究;由于活动货架具有空间利用率高的特点,Boysen等[9]对活动货架模式下的订单拣选优化问题建立了数学模型,并对开放巷道数量参数的灵敏度进行了实验分析;蔡安江等[10]针对具有多出/入库台的立体仓库堆垛机调度问题,建立了一种基于混合命令序列的堆垛机调度模型,并用遗传算法对该模型进行求解;赵金萍等[11]基于Flexsim对立体仓库出入库进行了仿真与优化;蒋美仙等[12]考虑到仓库的不同布局将会对仓库总拣货距离产生不同的影响,结合贯通式货架系统的思想,提出了一种改进的Fishbone仓库布局方法;吴迪等[13]分析了边远群岛物流体系的内在运作机理和特点,以物流节点选址、港口布局、仓储规划和航线配置为研究对象,构建出以物流成本最低为目标的优化模型;杨朋等[14]分析了多载具自动化存取系统的作业特点,建立了多载具自动化存取系统作业调度模型,并设计了求解该模型的遗传模拟退火混合算法;刘臣奇等[15]从候选节点集合策略、参数自适应调整以及选择算子等方面对蚁群算法进行了改进,并将其应用于求解自动化立体仓库固定货架拣选作业优化问题。
上述文献主要针对传统单区块类型仓储作业优化问题开展了相关的研究工作,对多区块类型仓储作业优化问题涉及较少。单区块类型仓储是指仓储系统仅仅包含前过道和后过道。如果仓储系统除了包含前、后两个过道外还有其他过道,则其为多区块类型仓储,具体如图1所示。特别是大型仓储系统,过道的引入给仓储作业增加了很大的柔性,因此该类仓储正逐步得到广泛应用。对于使用大型仓储系统的电商平台,比如淘宝、京东,在“双11”等类型的促销狂欢节中,在打价格战的同时,都希望将客户订单在最短时间内进行交付,以进一步提高服务质量和市场竞争力。因此,如何在带过道仓储中提高订单拣选作业效率是非常有价值的研究课题。
1 问题描述及模型构建
1.1 问题描述
以某大型网上超市仓储系统为例,其布局如图1所示。与传统单区块仓储系统相比,增加了过道布局。
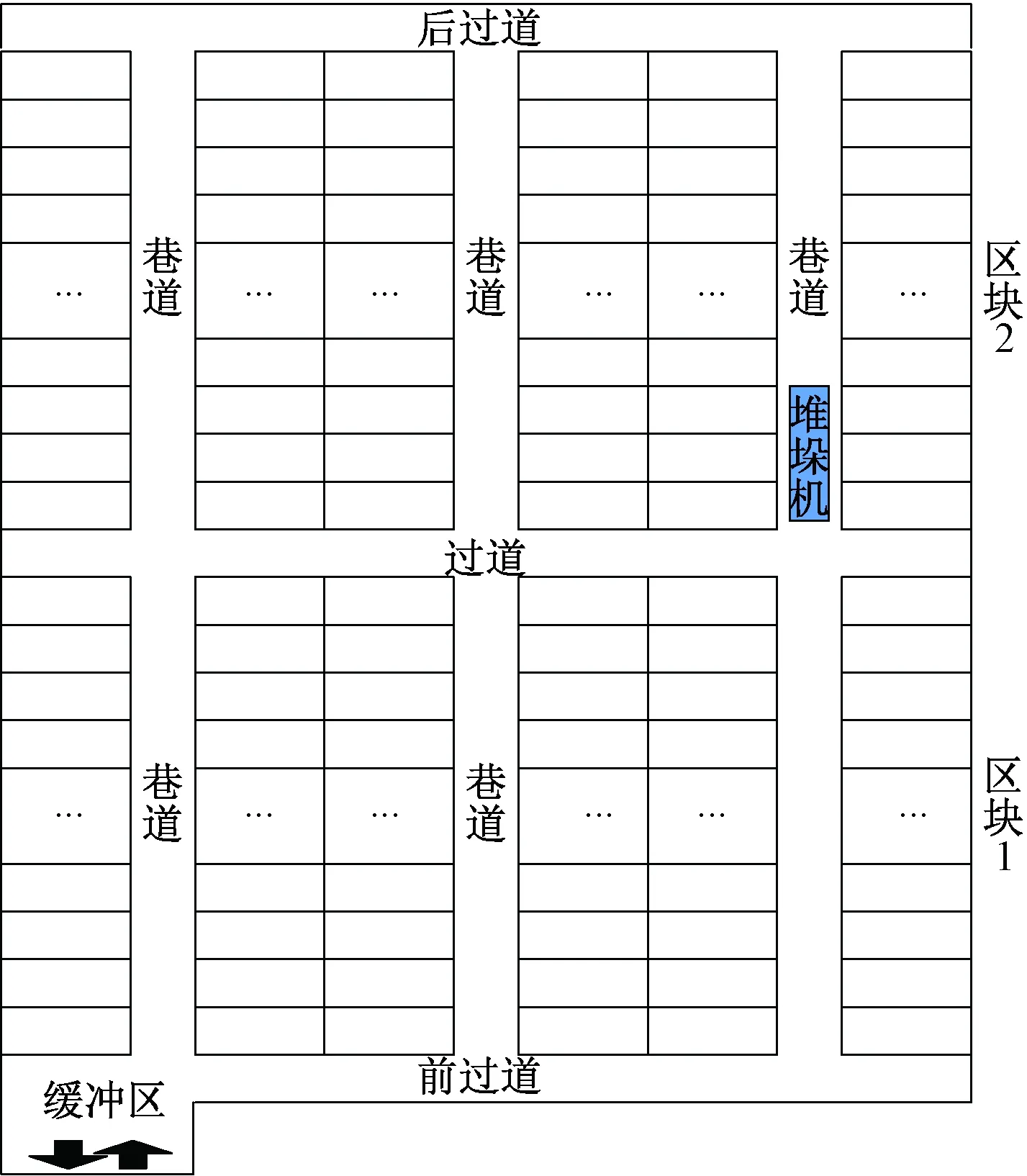
图1 仓储布局图Figure 1 Warehouse layout
从图1中可以直观地看到,堆垛机根据自身当前所处位置,通过选择合适的过道可以方便地实现从当前巷道进入到下一个巷道。该仓储系统具体作业流程为:堆垛机在缓冲区接到客户订单拣选指令后,自动进入相应的巷道开始拣选作业,直到完成既定的拣选任务后返回到缓冲区。
为研究方便,忽略堆垛机的启动和制动时间,设堆垛机的水平运动平均速度和垂直运动平均速度分别为vx和vy,且水平和垂直方向运动相互独立。堆垛机最大载货量为C,仓储每个仓位的长、宽、高分别记为L、W、H,巷道宽度为W1,过道宽度为W2,区块数为L1,每区块每巷道货架列数为L2,层数为L3,巷道数为L4。假设P={p1,p2,…,pn}为订单的n个待拣选货位,其货位pi(i∈{1,2,…,n})坐标可表示为(xi,yi,zi,bi),其中xi、yi、zi、bi分别为货位所在巷道号、货位所在货架的列号层号以及货位所在区块号,本文将缓冲区记为p0(0,0,0,1)。同时,每个待拣选货位货物的订单需求量记为wi。
定义1如果堆垛机在执行拣选任务的过程中连续经过货位pi和pj,则eij=1,否则eij=0。
在定义1中,堆垛机由货位pi到pj所用的时间可表示为:
(1)
式中:
A1=(W·|yi-yj|)/vx;
A2=(W·(yi+yj)+W1·|xi-xj|+W2)/vx;
A3=(W·((L1-yi)+(L1-yj))+
W1·|xi-xj|+W2)/vx;
A4=(W·(yi+yj)+W1·|xi-xj|+
W2·|bi-bj|)/vx;
B=(H·|zi-zj|)/vy。
定义2由于堆垛机载重量的限制,某一订单可能需要堆垛机进行R次拣选作业。如果待拣选货位pi在第r(r∈R)次拣选作业中完成,则gir=1,否则gir=0。
1.2 模型构建
求解该类型仓储作业优化问题的目标就是使完成所有订单的拣选任务所花费的时间最短,假设某订单拣选任务的集合为O,其数学模型和约束定义如下:
(2)
s.t.:
(3)
(4)
(5)
(6)
(7)
(8)
eij∈{0,1},∀i,j∈O;
(9)
gir∈{0,1},∀i∈O,∀r∈R。
(10)
式中:eij、gir、gjr为决策变量;tij为参数变量。其中,式(2)为目标函数;式(3)~(10)为约束函数。式(3)表示待拣选货位在拣选路径中只允许出现一次;式(4)限定堆垛机进行拣选作业所装载货物不能超过自身最大载重;式(5)和式(6)表示每个待拣选货位在拣选过程中不能形成自回路;式(7)和式(8)限定堆垛机拣选路径起始位和结束位均为出入库缓冲区处;式(9)和式(10)为决策变量的二进制值域约束。
2 多物种协同进化算法设计
由于所求优化问题的特性千差万别,因而不存在适合于求解所有类型优化问题的万能算法。本文将多物种协同进化思想引入到算法设计中,使用遗传算法[16]、粒子群算法[17]以及人工鱼群算法[18]竞争捕食机制进行协同进化,在提高单物种进化能力的同时,提高全部物种的整体寻优能力。
2.1 基于学习机制的多物种竞争捕食
关于多物种进化算法,已有学者进行了相关研究,比如黎明等[19]通过改变基因型到表现型的映射关系,使不同物种携带不同的遗传信息,然而,物种间并没有通过学习机制取其所长,在一定程度上会影响算法的求解效果。本文受达尔文生物进化论 “物竞天择,适者生存”的启发。将多物种协同进化思想引入到算法设计中,其基本原理是借鉴达尔文的生物进化论,将多个不同的物种,即遗传算法、粒子群算法和人工鱼群算法构建成一个完整的生态系统,通过物种间竞争捕食来完成信息共享,从而快速找到待求问题的最优解。其本质是每个物种具有不同的适应环境的能力,比如遗传算法擅长全局寻优,但其局部搜索能力差,容易出现早熟现象。粒子群算法收敛速度快,但其求解精度低。人工鱼群算法具有较强的全局搜索能力,但其搜索盲目性大,收敛速度慢。笔者将三者进行结合,充分利用各自的优点,实现优势互补,从而增强团队协作寻优的能力。具体协作机制为:在非竞争捕食阶段,每个物种按自己内部的进化机理进行觅食;在竞争捕食过程中,各个物种通过学习机制,学习其他物种的本领,使不同的物种能够优势互补,从而使整个生态系统中所有物种个体的质量都得到大幅提升,达到了在提高单个物种进化能力的同时,提高全部物种的整体寻优能力的目的。因而对多物种竞争共生启发式优化算法来讲,其求解效率及质量都得到了较大程度的提升。
为使多个物种协同进化,引入竞争捕食机制,具体工作原理为:在生物进化的过程中,由于自身或自然条件等因素,会出现对生存环境适应能力较差的个体,这些个体被其他物种捕食的风险大。为实现物种间竞争捕食,首先基于平均适应度找出捕食者与被捕食者,以平均适应度最大的物种为捕食者,其余物种均为被捕食者。被捕食的种群为更好地适应生存环境,需要总结被捕食的经验教训,即通过所谓的学习来不断提高自身的生存能力。为此,个体被捕食概率pi定义如下:
(11)
式中:fitness(·)为适应度函数。
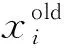
(12)
式中:Ω为全部物种的种群空间。
2.2 多物种种群多样性协同改善机制
种群多样性是物种适应环境能力的一种表征,对优化算法而言,则是解空间分布的一种度量。如果种群分布集中,则不利于解空间的开拓,容易导致算法陷入局部最优,从而降低求解效率及求解质量,而变异策略在一定程度上可以提高种群的多样性。基于上述考虑,有必要对基于变异机制的种群多样性进行调整改善。
为兼顾解空间全局的开拓以及局部的开发,笔者对全部物种的种群多样性进行协同改善。具体策略为:对全部物种中的所有个体按照适应度高低进行降序排列,然后计算所有非最优个体与最优个体间的距离,并按距离长短降序排列。为克服过度变异带来的随机性,只对适应度及距离排名后10%的个体进行变异。
2.3 多物种协同进化算法(MSCA)流程
Step1初始化参数。总体最大进化代数Gmax、每个物种的最大进化代数Gpmax、进化代数计数器t、种群规模M、交叉概率pc、变异概率pm、惯性权重w、学习因子c1和c2、步长step、人工鱼的视野范围Visual、尝试次数n、拥挤度因子δ,初始化每个物种的种群个体。
Step2全局搜索,t=t+1。
Step3局部搜索,遗传算法、粒子群算法以及人工鱼群算法进行单物种并行进化。
Step4产生随机数r。对于被捕食者,如果r>pi,则进行基于学习机制的多物种竞争捕食。
Step5多物种种群多样性协同改善。
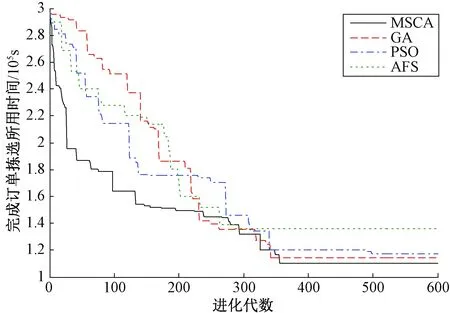
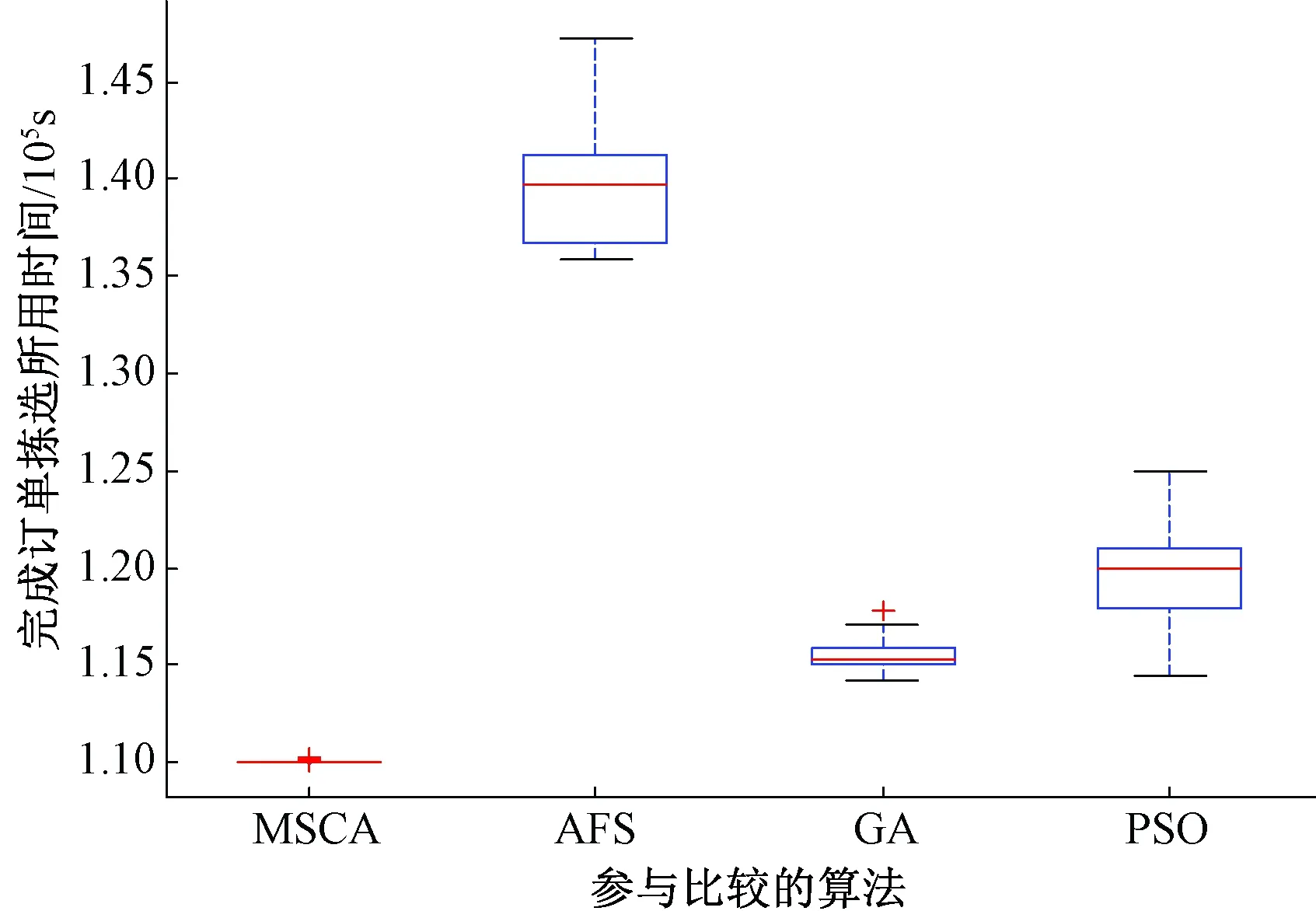
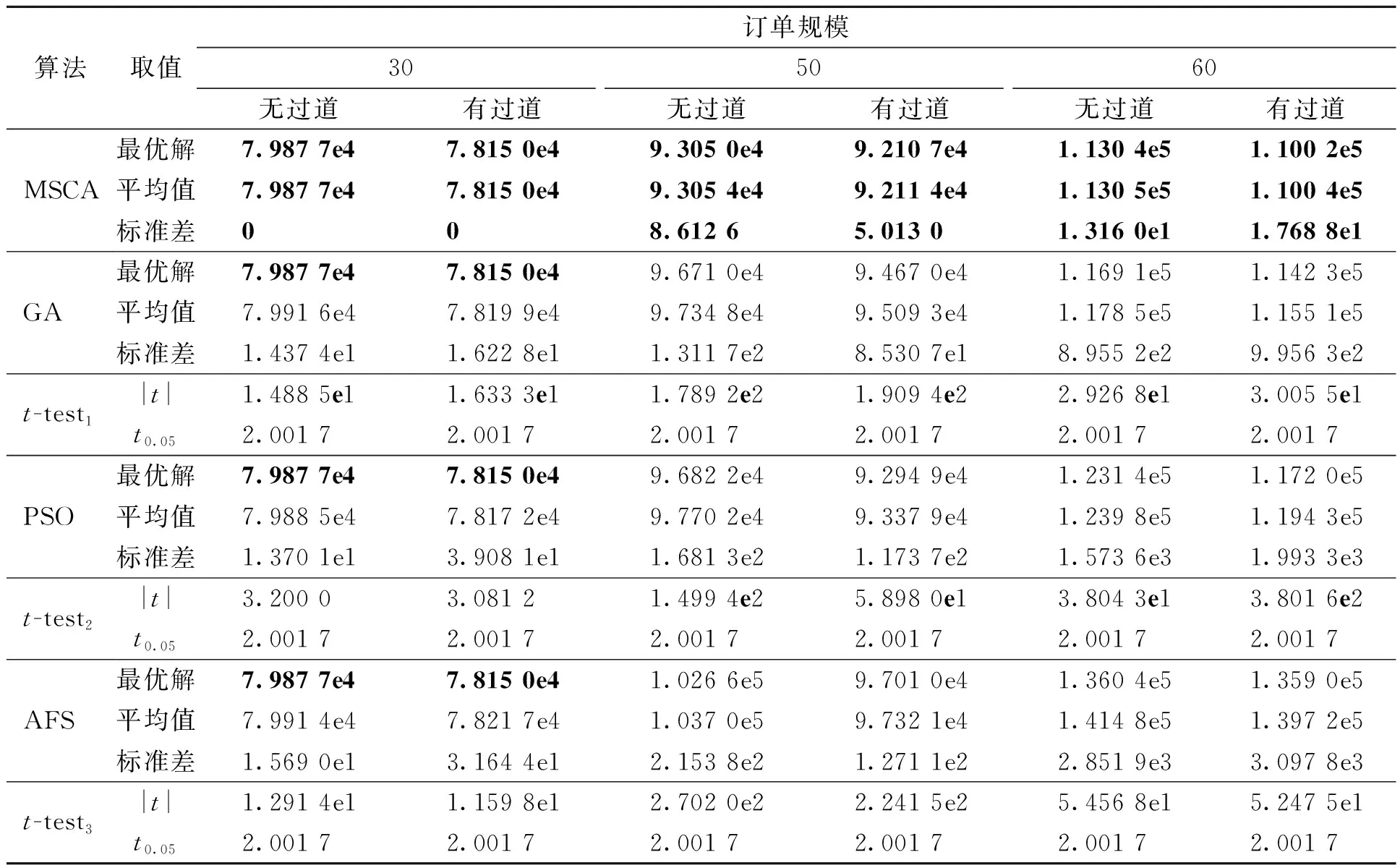
Step6如果t 算法具体流程图如图2所示。 图2 MSCA流程图Figure 2 Flow chart of MSCA 定义3设{Xk,k=0,1,…}是一离散序列,Xk的有限状态空间为S={γ1,γ2,…,γN},若对于任意的k≥0及γ0,γ1,…,γk-1∈S,都有下式成立: P(Xk+1=γj|X0=γ0,X1=γ1,…,Xk=γi)= P(Xk+1=γj|Xk=γi)。 (13) 则称{Xk,k=0,1,…}为有限Markov链。 定义4条件概率P(Xk+1=γj|Xk=γi)称为Markov链{Xk,k=0,1,…}在时刻k处于状态γi的条件下,在时刻k+1转移到状态γj的转移概率,记为pij(k)。如果pij(k)与时间k无关,则称{Xk,k=0,1,…}为齐次有限Markov链。 定理1MSCA的种群状态序列是齐次有限Markov链。 证明:假设种群中个体的位置称为个体的状态,由于求解问题规模有限,因而个体所有状态构成的空间S={ψ1,ψ2,…,ψN}是个有限集。同时,个体从当前状态ψi转移到下一个状态ψj无论经过遗传算法、粒子群算法、人工鱼群算法还是三者之间的竞争捕食,其转移概率pij(k)只与ψi有关,与时间k无关。因此MSCA的种群状态序列是齐次有限Markov链。 定义5假设Qk=max{F(xi)|i∈(1,2,…,U)}表示在第k代可行解中适应度最好的所有个体,如果满足下式: (14) 则MSCA是全局收敛的,式中Q*为待求问题的全局最优解集。 定理2笔者提出的MSCA具有全局收敛性。 证明: P{Qk∩Q*≠∅}=1-P{Qk∩Q*=∅}。 (15) 由于本文MSCA采用最优解保留策略,式(15)由贝叶斯条件概率公式又可表示为: P{Qk∩Q*≠∅}=1-P{Q1∩Q*=∅, Q2∩Q*=∅,…,Qk∩Q*=∅}= 1-P{Q1∩Q*=∅}×P{Q2∩Q*= ∅|Q1∩Q*=∅}×…×P{Qk∩Q*= ∅|Qk-1∩Q*=∅}。 (16) 令 ζ=max{P{Q1∩Q*=∅}, P{Qk∩Q*=∅|Qk-1∩Q*=∅}}, k=2,3,…。 (17) 则由式(16)、(17)可得 P{Qk∩Q*≠∅}≥1-ζk。 (18) 又因为ζ∈(0,1),所以 (19) 又因为 (20) 由式(19)、(20)可得 (21) 因此,本文提出的MSCA具有全局收敛性。 为了验证MSCA算法的性能,结合某企业给出的60个客户订单进行测试,并与标准遗传算法(GA)、标准粒子群算法(PSO)、标准人工鱼群算法(AFS)进行比较。实验在Windows 10系统平台,MATLAB7.0开发环境下进行。进化代数均为600,其中,对于MSCA,各子算法的进化代数均为50,子种群规模均为60;对于GA,种群规模为180,交叉概率及变异概率分别为0.80、0.06;对于PSO,种群规模为180,惯性权重w为1.3,学习因子c1和c2均为2;对于AFS,种群规模为180,步长为0.5,视野范围为15,尝试次数为30,拥挤度因子δ为0.618。自动化立体仓库系统参数:L=30 cm,W=50 cm,H=40 cm,W1=80 cm,W2=80 cm,L1=8,L2=100,L3=15,L4=7,vx=1 m/s,vy=0.5 m/s,C=500 kg。针对本文上述测试算例,图3为各算法求出的最优解随进化代数的变化趋势。为具有普适性,对不同规模的订单进行了测试,并对参与比较的算法各运行30次,同时,为兼顾公平性,各算法使用相同的目标函数评价次数,图4给出了订单规模为60时,30次运行结果的箱形图,表1给出了不同规模订单运行30次的最优解、平均值及标准差。同时,在算法性能上,为验证MSCA与GA、PSO及AFS是否存在显著性差异,又对算法的运算结果进行了基于均值的双样本t-test,本文首先假设参与对比的两个算法之间在性能上不存在显著性差异,并且显著性水平设为0.05。表1中的t-test1、t-test2和t-test3分别表示MSCA与GA、PSO和AFS的对比测试。 图3 最优解随进化代数的变化趋势Figure 3 Optimum change with generation 图4 30次最优解的箱形图Figure 4 Boxplots of 30 optimums 从图3可以直观地看出,本文提出的MSCA算法在收敛速度以及求解精度上明显优于其他3种算法。同时,图4表明对同一问题的多次求解,MSCA得出的最优解分布较为集中,表明该算法具有良好的稳定性。为进一步评估MSCA算法的性能,表1依据不同规模订单的求解情况,从仓库有无过道两个角度,将MSCA与GA、PSO及AFS进行了对比。从表1的统计结果来看,首先在最优解和均值方面,对于规模订单拣选问题的求解, 表1 不同规模订单各算法求解情况对比Table 1 Comparison among MSCA, GA, PSO and AFS 4种算法均显示出自身的优势,表明其具有较高的求解质量;其次,在标准差方面,MSCA标准差是最小的,特别是随着订单规模的增加,优势更为明显,从而表明MSCA具有较好的鲁棒性。关于MSCA的性能,t-test也对其进行了验证,在表1中,对任意规模订单的求解,|t|均大于t0.05,从而表明假设不成立,即MSCA与GA、PSO和AFS在性能上存在显著差异。MSCA之所以呈现这些特点,主要是由于笔者提出的基于学习机制的多物种竞争捕食及多物种种群多样性协同改善策略。首先,物种间的学习机制能够使物种快速获取整个生态系统当前时刻的最优解,从而能够引导自己向有利于找到全局最优解的方向搜索,从而提高了寻优效率;其次,多物种种群多样性协同改善策略通过物种间信息的共享,从全局角度改善了种群的多样性,这将在很大程度上降低算法进入局部最优的概率。因此这两方面有效增强了MSCA的全局开拓能力及局部探索能力。更为重要的是,表1揭示了带过道仓储在订单拣选效率上要好于无过道仓储。 为求解带过道的仓储作业优化问题,提出了一种多物种协同进化算法,通过引入学习机制,让物种间进行竞争捕食,从而实现优势互补;同时,提出多物种种群多样性协同改善机制,以快速提高每个物种的种群多样性。通过实例仿真可以看出,竞争捕食机制提高了求解效率,种群多样性协同改善机制扩大了解空间的寻优范围。最后验证了求解不同规模,特别是大规模订单拣选问题,MSCA相对GA、PSO及AFS算法的优越性,更为重要的是揭示了相对传统仓储,带过道仓储的订单拣选效率有明显的提升。因此,本文所研究问题的思路及成果为传统仓储的布局改造提供了参考。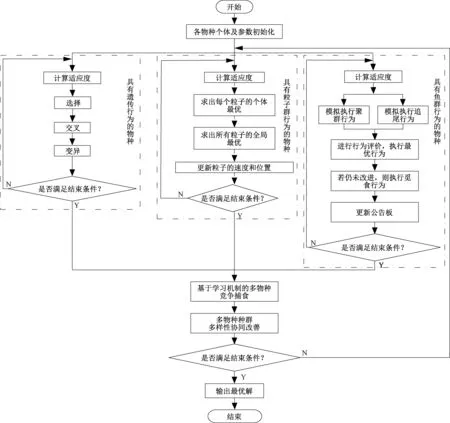
3 收敛性分析
4 算例验证与分析
5 结论

