基于改进防碰撞策略的两端式双堆垛机出入库优化研究
耿 赛,王 雷,李东东
(安徽工程大学机械工程学院,芜湖 241000)
自动化仓储系统(Automated storage and re‑trieval system,AS/RS)是一种新型的仓储技术,作为现代物流系统的核心部分,正越来越多地应用于各个行业[1‑3]。仓库的出入库效率直接影响到整个物流系统的效率,因此出入库路径的优化就成为提高整个物流系统效率的关键。堆垛机是AS/RS中运输和存取货物的主要设备,其中堆垛机拣选出入库货物的时间占其整个作业周期的50%左右,因此解决堆垛机行驶路径优化问题是提高自动化仓库效率的有效手段[4]。
国内外学者对立体化仓库出入库堆垛机路径优化问题做了大量的研究。Liu 等[5]、李媛媛等[6]、杨姣等[7]主要针对I/O 设在货架同一侧的情况,对堆垛机的不同工作模式建立了相关的数学模型,并分别结合遗传禁忌搜索算法、近似动态规划算法和遗传模拟退火算法对模型进行优化求解,提高了最优解的收敛速度。Emanuele 等[8]以仓库设计、存储策略和耗能作为重点对堆垛机进行路径优化。Bortolini 等[9]建立了分析模型来评估堆垛机在单一作业和复合作业中的预期时间。韩东亚等[10]以堆垛机出入库的复合作业和任务顺序为研究方向,根据问题的特点设计了两阶段启发式算法求解此问题,有效地提高了仓库拣选效率和堆垛机的作业方式。Lerher[11]对跨巷道堆垛机仓储系统进行研究,建立单、双指令情况下堆垛机的行程时间模型,并对时间模型进行性能分析。Torabizadeh 等[12]和Hao 等[13]建立新型的模型来研究仓储系统的可持续性可以通过存储策略、堆垛机停顿点策略和出入库调度策略等来有效地提高自动化立体仓库的效率。卞和营等[14]提出将I/O 分别设在货架两侧,并建立堆垛机的单一、复合作业模型,结合一种改进的遗传算法对模型进行优化求解。上述研究虽然最终取得了不错的货物出入库优化结果,但仅仅局限于算法上的优化,并没有对传统立体化仓库I/O台以及堆垛机的数量和位置布局上提出改良。蔡安江等[15‑16]在码头双堆码起重机调度的构思下,提出两端式I/O 同轨双车模式的双堆垛机调度模型,并结合防碰撞原则,用改进的化学反应优化算法进行求解,有效地提高了立体仓库货物出入库的调度效率。虽然该方法避免了两堆垛机在工作时发生碰撞,但防碰撞原则实现方法较繁琐且最终的任务分配也非最优,优化效果仍存在较大改进空间。基于此,本文以两端式双堆垛机模式下的立体仓库为基础,提出改进的防碰撞原则和最优防碰撞边界检验机制,并运用新型改进遗传算法(New improved genetic algorithm,NIGA)进行优化求解,最大限度提高大型立体仓库的出入库调度效率。
1 问题描述
1.1 两端式双堆垛机问题描述
在一般仓库的运输调度中,一般采取单端I/O、单堆垛机的调度模型,通过对单一作业、复合作业出入库任务的优化,来提高调度效率。但随着科学技术的发展,现代企业仓库规模不断扩大,这种传统模式下,仓库的优化效果往往不尽如人意。为了缩短堆垛机的最大工作行程、提高存取货物效率,蔡安江等[15]提出两端式双堆垛机模型。图1 为两端式双堆垛机立体仓库模型的结构图,在货架两端都设立相同规格的I/O 位置,货架之间的巷道上放置了两台规格相同的堆垛机。将堆垛机的最大行驶距离“一分为二”,左右两堆垛机分别负责自己的“工作区域”,极大地缩短了堆垛机的行驶路程,提高了大型仓库的出入库调度效率。
图1 中的堆垛机选用单立柱堆垛机,两堆垛机货叉相向,货叉可以左右伸缩,以便向两侧的货架存取货物。当两堆垛机同时工作时,要保证两堆垛机始终不会发生碰撞。即左端堆垛机处于货架第I列,右端堆垛机处于货架第I+1 列存取货物时,此时两堆垛机处于临界安全距离,仍可正常工作不会发生碰撞。

图1 两端式双堆垛机立体仓库模型结构图Fig.1 Structure diagram of the warehouse model with two‑end double stacker
立体仓库两端式双堆垛机的调度模型下,两堆垛机分别从对应的I/O 台完成出入库任务的存取,工作时互不干预,仅负责自己工作区的任务。所以完成一批货物存取所需的时间取决于两台堆垛机中耗时更长的一方。

式中TL和TR分别为同一巷道左端堆垛机和右端堆垛机完成各自任务所花费的时间。
堆垛机存取货物的工作方式有两种:(1)堆垛机每次从I/O 台出发,仅执行一个出库任务指令或者入库任务指令,称为单一作业(Single operation cycle,SC);(2)堆垛机从I/O 台出发,先执行一个入库任务指令,然后紧接着马上执行出库任务指令,称为复合作业(Double operation cycle,DC)。因为复合作业能够减少堆垛机往返I/O 台的次数,提高堆垛机的运行效率,因此优先选用复合作业方式。
若立体仓库为两端式布局,同一巷道上有两台堆垛机负责货物的出入库调度。现仅分析左堆垛机完成所有的单一作业任务,复合作业任务所用的时间为
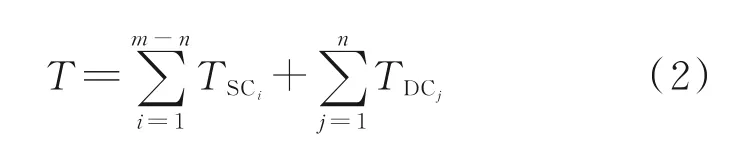
式中:TSCi为左端堆垛机完成第i个SC 作业时所运行的时间,TDCj为左端堆垛机完成第j个DC 作业时运行的时间。其中

式中:除TSCi和TDCj外,T表示堆垛机从一个货位到另一个货位所用时间;IOL为左侧出/入库台;Xi为堆垛机执行第i个单一任务时,出库/入库货位的位置;Xj1、Xj2分别为堆垛机执行第j个复合作业时,入库货位的位置和出库货位的位置。
式(2~6)仅分析了左端堆垛机存取货物的工作模型,右端堆垛机同理。当仓库接收到一批出入库混合任务指令时,需要两堆垛机协同工作拣取完所有的货物。因此要根据实际的工作情况,将一批出入库货物合理地分配给两堆垛机,在保证两堆垛机同时运行无碰撞的前提下,取得最优的调度效率。
因此,针对两堆垛机运行时无碰撞和任务分配最优两个关键问题,本文提出了改进防碰撞原则以及最优防碰撞边界检验机制,并运用NIGA 算法对包含SC、DC 两种工作模式的立体仓库双堆垛机模型进行出入库调度优化。
1.2 相关参数的基本假设
对于本文中的两端式双堆垛机立体仓库模型布局,为了研究更具有普遍性以及实用价值,参考文献[9]中的相关参数,现假设堆垛机作业时匀速运行,加速和制动时间忽略不计,不考虑货叉存取货物时间,设货位的长度和高度分别为l和h。根据上述假定参数可知,堆垛机从货位(x1,y1)到货位(x2,y2)的运行时间为
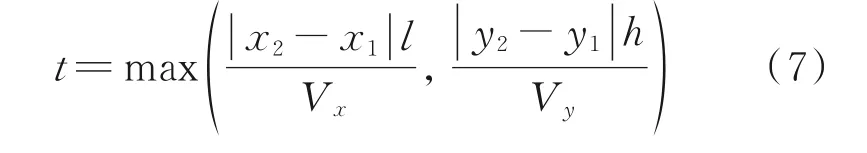
2 出入库调度模型
两端式双堆垛机出入库调度模式下,首要问题就是避免两堆垛机执行任务时发生碰撞以及合理分配左、右两堆垛机执行任务。因此本节首先提出了改进的防碰撞原则,并以此为约束条件,建立相关的双堆垛机调度模型,最后嵌入最优防碰撞边界检验机制。
2.1 改进的防碰撞原则
当接收到一批出入库货物混合订单时,把出库货物、入库货物对应货位的横坐标提取出来构成集合U。为了防止两端堆垛机在拣选、存放货物时发生碰撞,将这批货物分为两组,各组任务对应货位的横坐标分别构成集合L={xi1,xi2,…,xil}和R={xj1,xj2,…,xjr},在保证集合L中各元素均小于集合R中各元素外,为了方便后续优化算法的操作,将集合L和集合R中的货物横坐标元素xi1,xi2,…,xil以及xj1,xj2,…,xjr按从小到大的顺序依次排列。集合L中元素对应的出/入库任务交由左端堆垛机执行,集合R中元素对应的出/入库任务交由右端堆垛机执行。以此来划分两台堆垛机的工作区域,使左端堆垛机执行的出/入库任务对应货位的横坐标均小于右端堆垛机执行出/入库任务对应货位的横坐标,从而实现左右堆垛机在相同巷道同时作业时不会发生碰撞干预现象。
改进的防碰撞原则数学表达式为
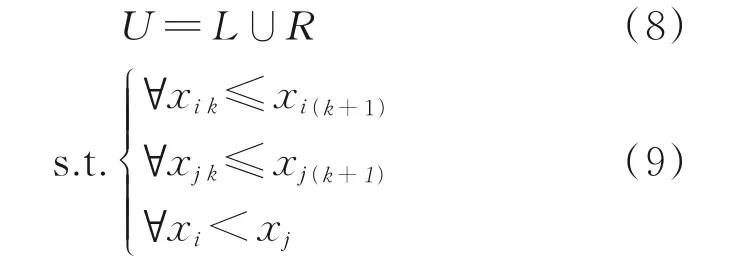

采用式(8,9)表示的改进的防碰撞原则,可将左、右两堆垛机负责执行的出/入库货物,根据其所处货位的列坐标从左往右按大小排列,划分为没有重叠部分的左、右两工作区域。
2.2 双堆垛机调度模型
虽然该调度模型下堆垛机型号完全一致,但是左、右堆垛机被分配的出库任务、入库任务的数目可能完全不同。假设左侧堆垛机需要执行n1个入库任务,m1个出库任务,右侧堆垛机需要执行n2个入库任务,m2个出库任务,取

由式(12)可知,两端式双堆垛机模式下,左侧堆垛机要执行Q1个DC 作业和Q2-Q1个SC 作业,右侧堆垛机要执行P1个DC 作业和P2-P1个SC 作业,结合式(2~6),参考文献[10]的相关内容,可得左、右两侧堆垛机完成各自任务所运行的总时间为
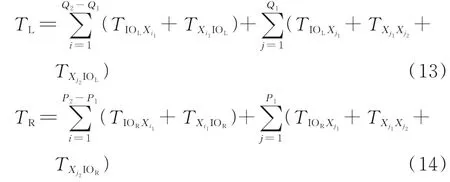
式中:TL为左侧堆垛机完成任务所用的时间;TR为右侧堆垛机完成任务所用的时间;IOR为右端货物出/入库台。
两端式双堆垛机模式下,堆垛机运输完一批出入库任务的总时间应该取决于两堆垛机中耗时较长的一方,综上所述,两堆垛机完成一批出/入库货物订单的总时间如式(1)所示。则两端式双堆垛机模式下完成这批出入库作业,双堆垛机的最优路径模型为

2.3 最优防碰撞边界检验机制
虽然上述改进的防碰撞原则可以将货架分为左、右工作区域,避免了两堆垛机在执行各自任务时发生碰撞。但如果左右区域划分不当,就会出现两堆垛机工作量差异较大的状况,导致任务量较少的堆垛机过早地完成任务,而任务量较大的堆垛机仍要“加班”工作的情况,极大降低了堆垛机的利用效率,与本文提出的双堆垛机提高货物出入库效率的想法相悖。于是为了解决这个问题,在改进的防碰撞原则的基础上,提出最优防碰撞边界检验机制。
最优防碰撞边界检验机制判断依据如下:根据改进的防碰撞原则得到左、右工作区分界线e;左、右堆垛机执行完各自分配任务所运行的时间TL、TR。
(1)当TL≥TR时,左、右工作区分界线左移取e左边较小元素,enew=U(i-1),将[enew,e]区间内横坐标对应的任务从左堆垛机负责的任务集合L中删去添加进右端堆垛机负责的集合R中,重新计算任务更新后,左、右堆垛机执行各自任务的运行时间TLnew,TRnew。比较两者大小:
①当TLnew≤TRnew时,此时分界线enew必为最优的防碰撞边界线。因为工作总时间T=max(TL,TR),所以比较TL与TRnew大小,若TL≥TRnew则保留最新的出入库任务分配结果,记录最优解Tbest=TRnew;反之保留原出入库任务分配结果,记录最优解Tbest=TL。
②当TLnew>TRnew时,令TL=TLnew,更新左、右堆垛机出入库任务分配结果,边界enew继续左移取U中最近的较小元素……按上述规则继续循环判断,直 至TLnew≤TRnew时,比 较TL与TRnew大 小,若TL≥TRnew则保留最新的出入库任务分配结果,记录最优解Tbest=TRnew;反之保留原出入库任务分配结果,记录最优解Tbest=TL。
(2)当TL ①当TLnew≥TRnew时,此时分界线enew必为最优的防碰撞边界线。比较TL与TRnew大小,若TR≥TLnew则保留最新的出入库任务分配结果,记录最优解Tbest=TLnew;反之保留原出入库任务分配结果,记录最优解Tbest=TR。 ②当TLnew 针对自动化立体仓库的两端式双堆垛机模式,在采用改进防碰撞原则的基础上,校验通过防碰撞原则得到的左、右工作区的划分界线e是否为最优分界线,从而保证了两堆垛机最优的货位分配,极大地缩短了堆垛机的最大行程,提高了出入库作业的效率。将上述的最优防碰撞边界检验机制嵌入到算法后续优化的每一次迭代中,根据TL、TR以及TLnew、TRnew的大小情况对左、右两堆垛机任务的分配结果进行自适应地调整,最终得到最优的任务分配方案(具体步骤见3.3 节) 为了解决自动化立体仓库出入库调度优化的多目标、多约束性等问题,通常采用启发式算法进行求解,常用的就是遗传算法。而在遗传算法中,交叉操作和变异操作对遗传算法的优化结果和收敛速度影响颇深,传统遗传算法中先进行交叉操作后进行变异操作,若种群的适应度值比较集中,交叉操作可能导致遗传算法(Genetic algorithm,GA)过早收敛,即使再进行变异操作,算法也很难跳出局部最优,在解决实际问题中,往往很难取到最优值[17‑18]。针对传统遗传算法“爬山能力差”,跳出局部最优能力弱的问题,本文提出了一种基于种群适应度疏密程度的不同而自适应调节进化过程的新型改进遗传算法NIGA。 NIGA 算法在优化过程中先求出种群个体适应度的最小值fmin、最大值fmax和平均值favg,再判断不等式“(fmax-favg)/(fmax-fmin)≥1/2”是否成立,若成立则说明当前种群的最大适应度值、平均适应度值的差值与最大适应度值、最小适应度的差值比较接近,且比值比1/2 大得越多,则说明此时种群的适应度值越密集,多样性不强,个体之间交叉产生优秀后代的几率不大,且算法容易陷入局部最优解,因此先执行变异操作,能增加算法跳出局部最优的能力,然后再执行交叉操作;若不成立则表明当前种群的最大适应度值、平均适应度值的差值与最大适应度值、最小适应度的差值存在偏差,且比值比1/2 小的越多,说明此时的种群的适应度值分布比较分散,种群的基因多样性丰富,个体之间交叉产生优秀后代几率较大,极大地提高了算法收敛效率,因此先执行交叉操作,再执行变异操作。 由于算法优化的目的是找到双堆垛机调度的最优任务执行顺序,高效地安排货物的出入库。若NIGA 算法采用二进制编码,则不能直观地描绘出堆垛机拣取货物的路径轨迹,反而会使编码过程变得更加复杂。因此本文NIGA 算法采用实数编码,每个实数代表待执行任务的编号。 每台堆垛机接收到的出入库任务指令按照前后顺序(左堆垛机Chrom1、右堆垛机Chrom2)分别编写成两段编码,每段编码中的实数代表着相应任务的序号。第1 段编码X=[x1,x2,…,xi,…,xm]表示堆垛机接收到的入库指令顺序,第2 段编码Y=[y1,y2,…,yj,…,yN]表示堆垛机接收到的出库指令顺序,Chrom=X∪Y=[x1,x2,…,xi,…,xM,y1,y2,…,yj,…,yN],其中M为入库任务的个数,N为出库任务的个数,xi为第i个入库货物在货架中的坐标位置,yj为第j个出库货物在货架中的坐标位置。自左往右,从X、Y的第一位开始,对应编号的出入库任务优先组成DC 作业,最后落单的出库或入库任务按SC 作业执行。例如,在经过防碰撞原则的任务分配后,左端堆垛机可能收到4 个入库任务和6 个出库任务的指令,随机生成的任务序列为Chrom1=[2,4,1,3,5,2,3,4,6,1],其中入库任务为X1=[2,4,1,3],出库任务Y1=[5,2,3,4,6,1],则左侧堆垛机编码Chrom1 对应的任务执行顺序是:先执行DC 作业:先执行入库任务2,出库任务5;再执行入库任务4,出库任务2;以此类推先执行完DC 作业,最后执行落单的出库任务6 和出库任务1 两个SC 作业,右端堆垛机工作模式与其一致。 目标函数为耗时较长一侧堆垛机完成所有任务运行时间的最小值,因此采用个体目标函数的倒数作为适应度函数,定义为 (1)选择操作 对群体中个体使用轮盘赌选择法进行选择操作,个体被选择的概率与适应度函数值有关,个体适应度值越高,被选中的概率越大,并在选择过程中加入精英保留策略,将上代中最优染色体保留到下一代。每个染色体被选中的概率为 式中:f(i)为第i个染色体的适应度值,m为种群个体的数目。 (2)交叉操作 分别对左、右两堆垛机的出/入库任务序列Chrom1、Chrom2 采用两点交叉,将相邻的两染色体分为一组,当每组染色体的随机概率rand≤pc时,从区间[1,m]随机选取两交叉点,对入库任务序列进行交叉操作,子代1 继承父代1 交叉点两侧的基因,中间缺失的基因按顺序从父代2 的基因中获得;子代2 同理获得。从区间[1,n]随机选取两交叉点对出库任务序列进行相同操作。用交叉后的子代染色体代替父代染色体。 (3)变异操作 分别对左、右两堆垛机的出/入库任务序列Chrom1、Chrom2 采用位置变异,每组染色体的随机概率rand≤pm时,从区间[1,m]随机产生两个变异点,对入库任务序列进行变异操作,交换两个变异点位置的基因形成新的染色体,同时从区间[1,n]随机产生两个变异点,对出库任务序列进行相同操作。用变异后的子代染色体代替父代染色体。 立体仓库出入库调度同轨双车的工作模式下,采用改进的防碰撞原则虽然能有效防止两车干预碰撞,但并不能使第1 次得到的货架的左右分界线e为最优分界线,所以在新型改进的自适应遗传算法的每一次优化迭代中插入满足改进防碰撞原则的最优防碰撞边界检测机制,对分界线e进行最优处理,结合算法,最终得到同轨双车调度模型的最优解。 改进的防碰撞原则划分左右两端货区初始任务种群的详细处理步骤如下: 步骤2 把出库货物、入库货物对应的货位坐标的横坐标提取出来构成集合U。且按照从小到大的顺序进行排列。设定左右两侧堆垛机工作区域的分界线为e=U(i),i∈[1,n]。工作区域分界线e代表的含义为从第1 列到第e列货位的货物为左端堆垛机的工作区域,第e+1 列到第I列为右侧堆垛机的工作区域。 步骤4 判断tL≤tR,若成立,则令i=i+1,e=U(i),i∈[1,n],转步骤3;否则,执行步骤5。 步骤5 左右两侧堆垛机任务分配完成,获得初始种群工作序列。从第1 列到第e列货位为左侧堆垛机的工作区域,此工作区的出/入库货物由左侧堆垛机完成;从第e+1 列到I列货位为右侧堆垛机的工作区域,此工作区的出/入库货物由右侧堆垛机完成。 步骤6 将左端堆垛机所分配的出/入库货物的任务序列随机排序,生成若干任务序列;对右端堆垛机所分配的出入库货物的任务序列随机排序,生成相应的任务数列。 满足改进防碰撞原则的最优防碰撞边界检测机制的具体操作如下: 步骤1 把左端堆垛机负责的左侧工作区的出入库任务种群根据式(13)分别计算出它们的个体适应度值FL1,FL2,…,FLn1,把右端堆垛机负责的右侧工作区的出入库任务种群根据式(14)分别计算出他 们的个体适应度值FR1,FR2,…,FRn2,其中n1、n2分别为左右两端堆垛机负责出入库任务序列的 个 体 个 数,然 后,定 义TL= min(FL1,FL2,…,FLn1),TR= min(FR1,FR2,…,FRn2)。 步骤2 判断TL与TR的大小。 步骤3 如果TL≥TR,工作区分界线enew=e(i-1),即e取货位坐标的横坐标集合U左侧上一元素,根据新工作区分界线重新调整两堆垛机任务分配后,计算两堆垛机的运行时间TLnew,TRnew。判断TLnew≤TRnew,如果成立,记录下TRnew,比较TL与TRnew大小,若TL≤TRnew,记录最优解Tbest=TL,左右两堆垛机的任务分配结果不变,若TL>TRnew,记录最优解Tbest=TRnew,将[enew,e]区间,原属于左堆垛机任务序列的对应任务删除,添加到右堆垛机的任务序列中;如果不成立,同理循环。 步骤4 如果TL 在上述的最优防碰撞边界检测机制操作步骤中,重新划分的左右工作区分界线enew,仍然约束着如下关系:左侧堆垛机分配任务所处货架的最大横坐标小于右侧堆垛机分配任务所处货架的最小横坐标,所以经过最优防碰撞原则检测机制优化后的左右堆垛机分配的任务依然满足改进的防碰撞原则,能够有效防止两堆垛机在运行时发生碰撞干预的现象。将最优防碰撞原则检测机制在NIGA 算法的步骤7 中调用,插入到在NIGA 的每一次优化迭代中。 嵌入改进防碰撞原则以及最优防碰撞原则检测机制的NIGA 算法对立体仓库同轨双车出入库调度优化的具体步骤如下: 步骤1 设定初始参数,包括两端I/O 台O1、O2的坐标,设置初始种群的规模m、以及NIGA 算法的最大迭代次数MAXiter。 步骤2 调用经过改进的防碰撞原则产生的两个初始分配的种群Chrom1、Chrom2。Chrom1代表左端堆垛机需要负责的工作序列,种群Chrom2 代表右端堆垛机需要负责的工作序列。 步骤3 设定初始代数iter=0,若iter 步骤4 判断(fmax-favg)/(fmax-fmin)≥1/2 是否成立,如果成立,则分别对种群Chrom1、Chrom2 先进行选择操作,然后进行变异操作,最后进行交叉操作;反之,先对种群进行选择操作,然后进行交叉操作,最后进行变异操作。 步骤5 经过上述步骤,分别记录进化后Chrom1、Chrom2 两种群的最优值TL、TR。 步骤6 调用最优防碰撞边界检验机制的具体步骤,检验左、右工作区分界线e是否最优,调整左右两堆垛机的任务分配,并记录最优解Tbest;转步骤4。 步骤7 迭代结束,输出最优解Tbest以及最优解对应的两堆垛机最佳调度序列Chrom1、Chrom2。 嵌入改进防碰撞原则和最优防碰撞边界检验机制的NIGA 算法流程图如图2 所示。 图2 嵌入改进防碰撞原则的NIGA 算法流程图Fig.2 Flow chart of NIGA algorithm embedded with improved anti-collision principle 改进后的NIGA 算法,可以根据种群适应度值的集中分散程度,来调整算法的进化结构,有效地提高了算法跳出局部最优的能力,加快了算法的收敛速度。结合改进防碰撞原则和最优防碰撞边界检验机制后,NIGA 算法有效地解决了两堆垛机工作时发生碰撞的问题,并为它们分配了最优的作业区域和任务序列,最终获得了理想的堆垛机任务分配方案。 为证明本文所提出改进遗传算法的有效性,现通过一个具体的立体仓库货物出入库实例来进行验证。某企业的自动化立体仓库的一个货架有12层80 列,共有960 个货位。每个货位的位置固定,且大小相同,每个货位每次最多存储一个货物。货架的两端各分布着一个I/O 台,仓库的巷道左右两端分别放置了型号规格完全相同的两堆垛机,两堆垛机在巷道上可以同时工作,且分别为各自负责的I/O 台执行货物的出入库作业,货架及两堆垛机的具体信息见表1。 表1 立体仓库规格信息及堆垛机配置信息Table 1 Specification information of warehouse and con⁃figuration information of stacker 立体仓库内有一批要执行的出入库任务,包含17 个入库任务和15 个出库任务,任务坐标位置信息如表2 所示。 表2 出入库任务坐标Table 2 Coordinates of storage and retrieval tasks 为了验证本文算法的可行性以及优越性,以NIGA 算法为基准,分别利用GA,自适应遗传算法(Adaptive genetic algorithm,AGA)对上述的一批出入库任务坐标进行优化求解。对初始参数进行设定,初始种群的规模m=100,最大迭代次数MAXiter=100,pc=0.6,pm=0.2。使用matlab2018b对上述立体仓库参数以及出/入库任务信息进行编程实现,分别用NIGA、GA、AGA3 种算法对上述所给的出入库货物相关信息进行优化。 由图3 可知,NIGA 算法和AGA 算法随着迭代次数的增加均收敛到了最优解307 s,而NIGA算法在第9 代就收敛到最优值,其迭代速度更快,而GA 算法则陷入局部最优,在第14 代才得到局部最优解328 s,具体比较结果见表3。与GA、AGA 算法相比,NIGA 算法收敛速度更快,跳出局部最优能力更强,迭代效果更优。 图3 针对表2 任务的目标函数进化曲线Fig.3 Evolution curves of the objective function for tasks in Table 2 表3 3 种算法结果对比Table 3 Comparison results of three algorithms 由NIGA 算法对表2 的出入库货物序列优化后的最优解输出的左堆垛机调度序列为(3 8 5 4 7 6 2 1 1 7 4 3 5 6 2),右堆垛机调度序列为(4 9 2 3 6 7 5 8 1 3 7 8 1 2 6 4 5)。相应的堆垛机工作路线如图4 所示。 根据图4 可知,通过NIGA 算法对表2 中的出入库货物信息进行优化,工作区的分界线为e=40,即从货架的第1~40 列的出入库货物由左堆垛机负责调度,货架第41~80 列货物由右堆垛机负责调度,左右两堆垛机分别在自己的工作区域内工作,不会发生碰撞干预现象。 图4 针对表2 任务得到优化后两堆垛机的行驶路线图Fig.4 Driving routes of the two stackers after optimization for tasks in Table 2 为了证明嵌入改进防碰撞原则以及最优防碰撞边界检验机制后的NIGA 算法能为堆垛机最大程度合理分配任务,使出入库调度结果达到最佳,同文献[15]的防碰撞原则以及任务分配机制作比较,用本文改进遗传算法对文献[15]中的出入库任务数据进行优化求解。两算法参数调整一致,NI‑GA 算法优化后堆垛机运行时间进化曲线如图5 所示,两堆垛机行驶路线图如图6 所示。文献[15]中利用改进的化学反应优化(Improved chemical reac‑tion optimization,ICRO)算法求解得到的优化值为312.67 s,两堆垛机的工作区间的分界线为e=39,而利用本文NIGA 算法求得的优化值为251 s,减少了61.67 s,得到的两堆垛机的工作区间的最佳分界线为e=37。 图5 目标函数最优值进化路线图Fig.5 Evolution curve of the objective function 图6 两堆垛机优化后行驶路径图Fig.6 Driving routes of the two stackers after optimization 针对目前大型企业的自动化立体仓库规模较大,调度难的现象,分析了两端式双堆垛机出入库调度问题,建立了相应的数学模型。在该模型的基础上提出了改进防碰撞策略以及最优防碰撞边界检测机制的解决方法,并提出一种新的改进遗传算法进行优化。对比实验结果表明,该算法能够根据种群适应度值的集中分散情况,从而自适应地调节进化过程中交叉操作、变异操作的先后顺序,加快了算法的收敛速度,提高了算法避免陷入局部最优的能力,并在每次迭代中嵌入改进防碰撞策略以及最优防碰撞边界检测机制,有效地确定了两堆垛机工作区的最佳分界线,避免了堆垛机运行中的碰撞,平衡了两堆垛机的工作时间,有效地解决了大型自动化立体仓库双堆垛机的出入库调度问题。本文对立体仓库的布局仅考虑了两端式I/O 台布置,在实际工作中,为了生产调度的方便,I/O 台也可能放置在货架中间。另外,本文假设堆垛机的水平和垂直速度是恒定的,堆垛机每次完成任务后都返回至I/O 台。因此在今后的工作中,堆垛机的水平、垂直加减速和停靠点的位置选择也是未来研究中有待解决的问题。3 出/入库调度路径的优化
3.1 编码设计
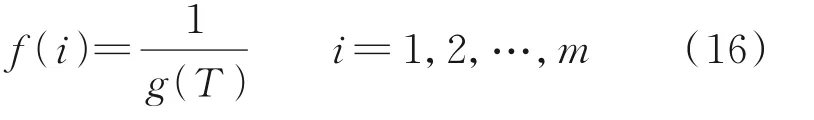
3.2 算法设计
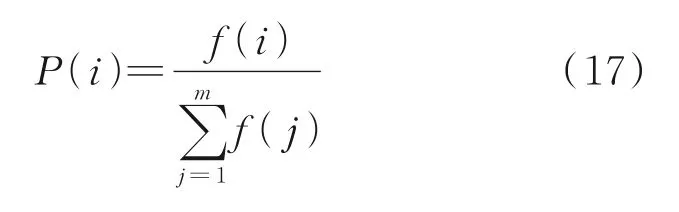
3.3 算法步骤

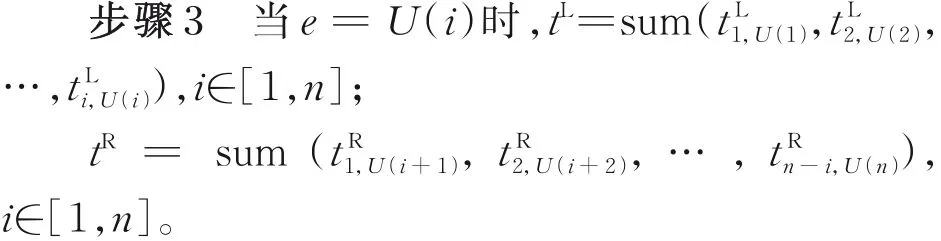
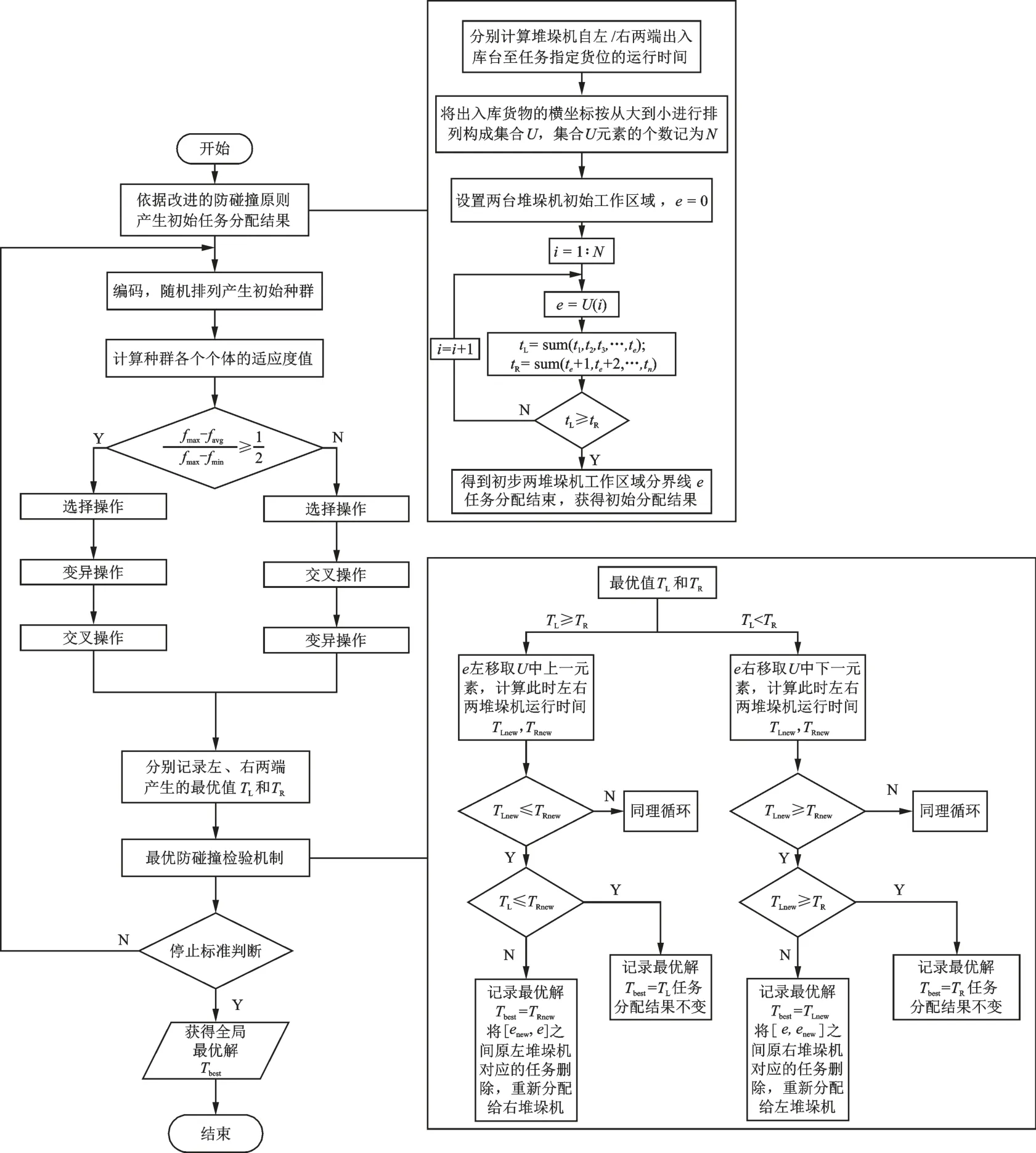
4 实验仿真及分析

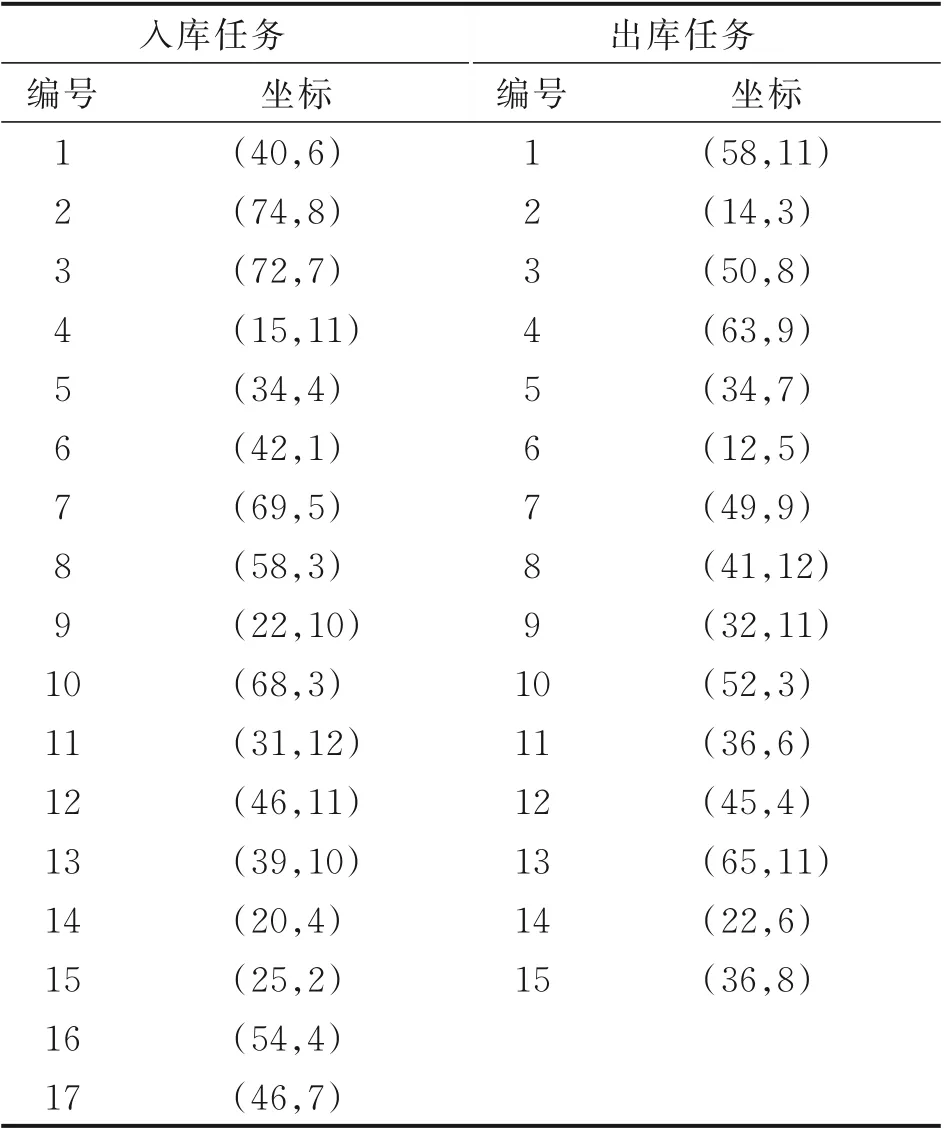


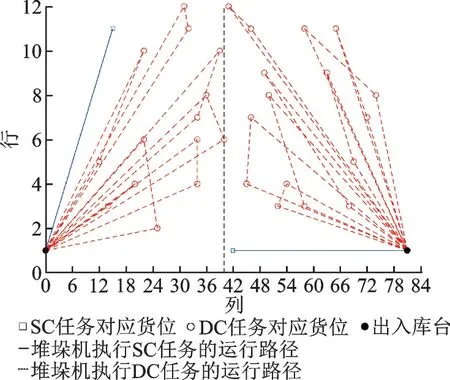
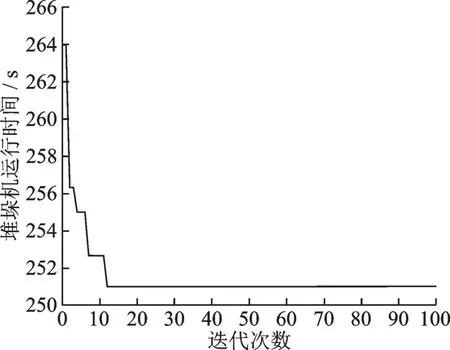

5 结 论

