采用K-means的脑肿瘤磁共振图像分割与特征提取

宗晓萍，田伟倩

河北大学 电子信息工程学院，河北 保定071000

1 前言

随着医学成像技术的发展，早期通过解剖来了解大脑构造和治疗的方式已经被成像技术所取代。医学成像技术主要包括CT扫描、超声波和核磁共振（Magnetic Resonance Images，MRI）等。这些采集到的医学影像，用来重建人体内部器官的三维图像，辅助医生进行疾病诊断和治疗。其中，MRI以其较高的安全性[1]（无放射性辐射）和对人体软组织成像分辨率高的特点，成为脑部肿瘤诊断与治疗中最常用的医学影像[2]。

医师进行脑部肿瘤诊断与治疗，首先需要对肿瘤进行检测和分割。然而，手动定位和分割需要花费大量的时间。同时，精确的分割对医师的专业技能有很高的要求。所以，利用计算机技术自动分割脑肿瘤这一领域快速发展起来，以减轻医师的工作压力。图像分割是图像分析和计算机视觉中最重要的任务之一[3]。脑肿瘤的自动分割就是根据图像区域内的相似性以及区域间的差异性把肿瘤（感兴趣区域）从图像中分离出来。对于医学图像的自动分割，图像的特征提取是一个核心技术，是病灶准确分割的前提。同时也是制约图像处理中其他相关技术发展和应用的瓶颈[4]。

对图像纹理的准确描述，在图像分割中非常重要。纹理特征提取的目标是：提取的纹理特征维数小、鉴别能力强、计算量小。灰度共生矩阵（Gray Level Co-occurrence Matrix，GLCM）是涉及像素距离和角度的矩阵函数，它通过计算图像中一定距离和一定方向的两点灰度之间的相关性，来反映图像在方向、间隔、变化幅度及快慢上的综合信息，被广泛应用于提取图像纹理特征[5]。在核磁图像上应用GLCM，可以提取出脑瘤图像的纹理特征，但是由于纹理特征只是图像表面的一种属性，并不能完全的区分肿瘤和健康组织。不变矩方法[6]由于其具有旋转、平移、尺度等特性的不变特征，能将图像分解为有限的特征值，并对比所提取出的同一病人的肿瘤图像的形状不变特征。但是不变矩方法对噪声很敏感。单独使用不变矩特征并不能提供肿瘤分割所需的有效特征。

本文结合GLCM和不变矩方法，提取出脑瘤图像的纹理特征和几何特征，同时结合图像的灰度信息对肿瘤图像进行分割，更好地辅助医生进行判断。本文首先应用K-means算法，设定簇数为4，利用脑部MRI各个部分灰度值不同的特点对各点聚类，提取出肿瘤图像；应用灰度共生矩阵提取出肿图像的纹理特征，同时应用不变矩方法提取出肿瘤图像的七个不变矩特征，最后计算上述特征参数的相关系数，并归纳出独立性高的一组特征参数以表征脑部肿瘤图像的纹理和几何特征参数。

现有的矩方法众多，比如三值径向谐波傅里叶矩，四元数极调和傅里叶矩等。但是与其他方法相比较，不变矩方法更为适合于描述提取出的脑肿瘤图像特征。三值径向谐波傅里叶矩[7]是基于三值数理论和径向谐波傅里叶矩（RHFM）提出的，三元径向谐波傅里叶矩（TRHFM）对立体图像进行整体处理，并在此基础上提出了一种鲁棒的立体图像零水印算法，文章所提出的立体图像零水印算法对各种非对称和对称攻击具有很强的鲁棒性，与其他零水印算法相比具有一定的优越性。还有四元数极调和傅里叶矩[8]（QPHFM）用于彩色图像处理，并对QPHFM的性质进行了分析。将chebyshevs-傅里叶矩（CHFM）扩展到四元数chebyshevs-傅里叶矩（QCHFM）之后，比较实验，包括图像重建和彩色图像对象识别，对QPHFM和Quaternion Zernike矩（QZM）、Quaternion伪Zernike矩（QPZM）的性能，采用四元数正交Fourier-mellin矩（QOFMM）、QCHFM和四元数径向谐波傅里叶矩（QRHFM）进行了计算。实验结果表明，QPHFM在无噪声、无噪声的条件下，能够实现理想的图像重建和不变对象识别。

2 K均值算法

图像分割可以定义为以简化图像为目的，把数字图像分割成不同的区域，这使图像更有利于可视化分析，图像分割在大部分医学图像分析中是最主要的并且有显著意义的过程。目前，已经有很多种方法应用于图像分割，有阈值法、区域生长法、监督和无监督聚类技术。其中，聚类是一个将数据集划分为若干类或簇（cluster）的过程，使得同一簇内的数据具有较高的相似度，而不同簇中的数据对象则是不相同的。

目前从脑部MRI中分割出肿瘤的方法已经有很多，文献[9]借助支持向量机良好的分类性能，SVM分类器用于像素的分割，将像素分为两类，采用核支持向量机进行无监督学习，取得了良好的结果；文献[10]介绍了阈值分割法，文献[11]介绍了区域生长法：检测图像中的像素，根据预定义的相似度准则，将具有同质属性的相邻像素结合在一起，实现图像分割；应用模糊聚类检测MRI图像中肿瘤，通过在簇和数据点之间的距离的基础上，将每个数据分配到各自的聚类中心，由于FCM是一种迭代算法，所以它的计算时间久。

聚类可以被定义为一组像素，所有的像素通过一种相似的关系被定义。聚类被认为是无监督分类技术。之所以被称为是无监督分类是因为这种算法根据用户给定的标准自动分类物体。脑部MRI图像由于在成像过程中会受到噪声、场偏移效应等的影响，导致原始图像组织边界模糊，难以辨认一些细微结构，因此在对图像进行分割前，需要先对原始图像进行预处理。本文中在对输入图像进行预处理（中值滤波，去除非脑组织）后，应用K均值聚类算法对脑部肿瘤图像进行分割，对分割出的肿瘤图像进行特征提取，最后实现肿瘤检测的目的。过程方块图如图1。

图1 实验流程

2.1 K-means算法

K-means算法过程如下：

（1）令X1，X2，…，XN为输入图像的N个数据点，设定簇数为K。

（2）随机选取C1，C2，…，CN个聚类中心。

（3）算出每个像素到每个聚类中心的距离。

（4）按照最近的类进行划分。

（5）按下式更新聚类中心：

其中，i=1,2,…,K，mi是Ci中目标的数量，Ci是第i个聚类中心，Cj是第j个聚类中心。

（6）重复上述过程，直到达到收敛条件。

2.2 实验结果

实验对象（图2）为含有脑肿瘤的核磁共振图像，图片来源为Kaggle数据集（https：//www.kaggle.com/），图像大小为：256×256像素。实验环境为Matlab2016b，在本文设计的程序中，聚类数量设置为4，在Matlab中首先对图像进行预处理，中值滤波，然后应用K均值算法利用脑部图像不同部分灰度值不同进行聚类，以达到分割图像的目的。图3为经过算法处理后，脑部MRI分割提取出的脑部肿瘤图像。

图2 脑部MRI图像

图3 提取出的肿瘤图像

3 纹理特征提取方法

3.1 彩色图像的纹理特征提取

一幅图像在RGB空间中被量化为256种颜色，在提取图像的特征时，将纹理特征与颜色特征相结合[12]，利用量化的HSV颜色空间，同时提取颜色特征和纹理特征，该方法可以有效地提取图像特征，对大规模图像数据集的图像检索具有足够的鉴别能力。

文中提出了新的纹理描绘子SED，SED的一个主要问题是如何定义结构元素。颜色、纹理和形状在基于内容的图像检索中起着重要作用，同一类图像的局部结构往往具有一定的相似性，在某种意义上，可以认为图像的有意义的内容是由许多结构元素组成的，如果提取这些结构元素并对它们进行有效的描述，它们就可以作为对不同图像进行比较和分析的共同基础。这样，这些结构元素就可以有效地表示图像。方向在图像描述中起着重要的作用，结构元素由五个分别表示五个方向的结构元素定义。SED能够有效地表示图像特征，能够同时提取和描述颜色和纹理特征。SED有五个2×2矩阵如图4所示。

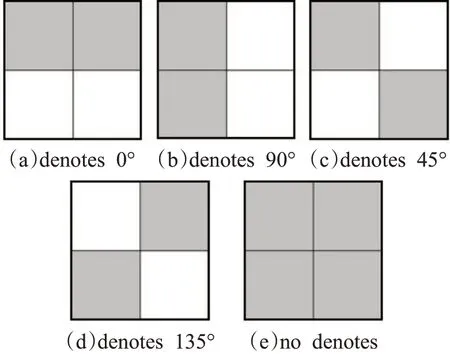
图4 SED中的五个结构元素

3.2 基于灰度共生矩阵的纹理特征提取

本文所处理为灰度图像，采用灰度共生矩阵进行纹理描述，在空间中，灰度分布反复交替形成纹理，因此，在一定距离条件下，两个像素的灰度一定存在一定的关系。

令O是定义两个像素彼此相对位置的算子，L为灰度级，h(i,j)为图像上灰度分别为i和j的像素对(1≤I,j≤L)在指定位置关系下出现的次数，由h(i,j)构成的矩阵H就称为灰度共生矩阵，θ为灰度共生矩阵的生成方向，通常取0°、45°、90°和135°四个方向。

3.2.1 灰度共生矩阵的参数

一般不直接应用灰度共生矩阵，为了更直观地对纹理进行描述，在灰度共生矩阵的基础上对其进行提取二次统计量。灰度共生矩阵计算量很大，所以取四个比较常用的特征来提取肿瘤部分的纹理特征。

Haralick等人[13]定义了14个灰度共生矩阵特征参数来进行纹理描述，Ulaby等人[14]研究发现：在基于GLCM的14个纹理特征中，仅有四个特征是不相关的，这四个特征既便于计算又能给出较高的分类精度。四个特征如下：

（1）角二阶矩（能量）

角二阶矩是灰度共生矩阵所有元素值的平方和，又称能量。它反映纹理灰度变化均匀程度和纹理粗细程度。

（2）对比度

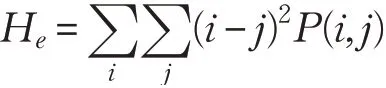
对比度是灰度共生矩阵主对角线附近的惯性矩，反映了影像的清晰度和纹理的沟纹深浅。

（3）相关

它度量空间灰度共生矩阵的元素在行或列方向上的相似程度，因此，相关值大小反映了图像中局部灰度相关性。

（4）熵

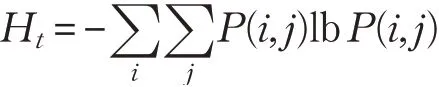
熵度量影像纹理的随机性。当灰度共生矩阵中所有值均相等时，它取得最大值；相反，如果共生矩阵中的值非常不均匀时，其值较小。

对于纹理特征图像的提取，需要对灰度共生矩阵的计算结果作适当处理。最简单的方法是取不同方向（0°、45°、90°、135°）的偏移参数，做其灰度共生矩阵，分别求取其特征指标，然后对这些特征指标计算其均值和方差。这样处理就抑制了方向分量，使得到的纹理特征与方向无关。

3.2.2 实验结果

本文对所提取出的五幅肿瘤图像计算其灰度共生矩阵，应用MATLAB2016进行实验，获取灰度共生矩阵的四个参数，实验结果如表1及图5所示。

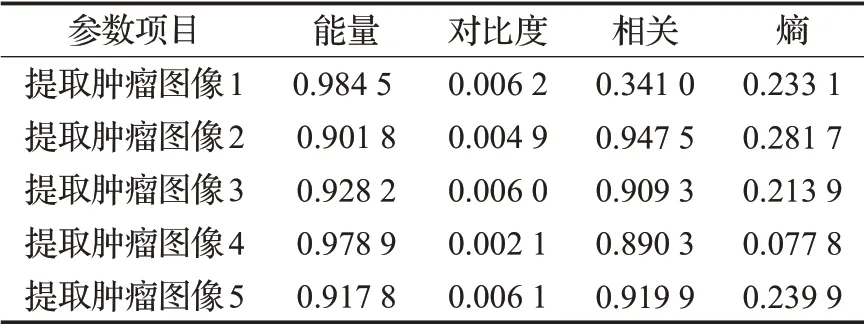
表1 灰度共生矩阵特征量

3.3 不变矩

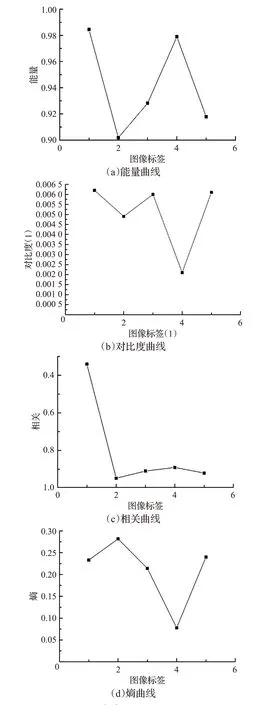
图5 灰度共生矩阵特征量

矩特征主要表征图像区域的几何特征[15]，又称为几何矩，由于其具有旋转、平移、尺度等特性的不变特征，所以又称其为不变矩。在医学临床中，脑肿瘤有原发和继发两大类，良性肿瘤和恶性肿瘤在形状上有很大的差别，大部分良性肿瘤形状规则，边缘光滑，轮廓清晰，与

周围的脑组织有比较清晰的界限；而恶性肿瘤大部分形状不规则，边缘模糊粗糙。

3.3.1 不变矩参数

不变矩：数字图像f(x,y)的二维(p+q)阶原点矩定义为：

式中，p=0,1,2,…和q=0,1,2,…是正整数。(p+q)阶中心距为：

可以由此推导出对平移、比例、镜像、旋转都不敏感的7个二维不变矩的集合。

3.3.2 实验结果1

对同一病人不同切片的脑部肿瘤图像进行分割并提取不变矩参数，实验结果如图6～图8。

在同一病人肿瘤的不同切片中，恶性与良性肿瘤的变化同时也会产生明显不同的几何参数变化。从表2可以看出，同一病人不同切片的不变矩参数值有很大的不同。因此，脑部肿瘤特征提取中，几何不变矩作为一个重要的特征来描述所提取肿瘤图像的几何参数，既可以表征肿瘤的形状特征，又可以从不同角度表示同一病人的病情。

图6 脑瘤患者MRI图像

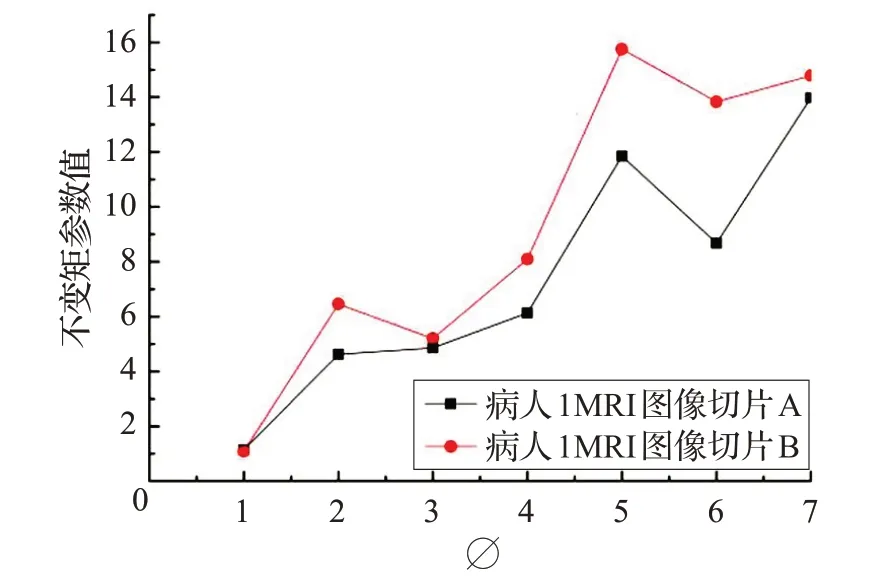
图7 病人1不变矩参数值

图8 病人2不变矩参数值

3.3.3 实验结果2

本文应用不变矩对所提取的肿瘤图像（图9）进行180°旋转，结果如图10所示。

用MATLAB计算出五幅图像的七个不变矩的值，如表3所示。

3.4 参数选取

本文用相关性系数来度量上述参数的相关性，绘制五幅图像的四个灰度矩阵特征参数和七个不变矩参数的相关系数矩阵[16]，见表4所示。（1～4为灰度共生矩阵参数，5～11为不变矩参数）

表2 同一病人不同切片不变矩

图9 原始分割图像

图10 旋转180°后的图像

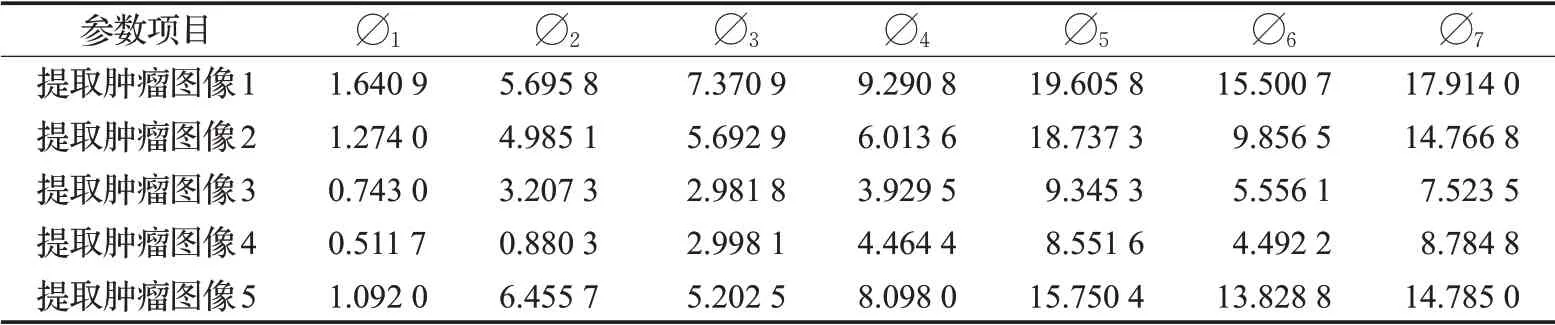
表3 分割出的脑肿瘤图像的不变矩参数值

表4 11个参数的相关系数矩阵

观察图11，筛选出相关系数值较小的一组特征参数为：能量∅1、∅6。参数之间的相关系数的大小取值反映了参数之间的相关性程度，即参数之间的相关系数越大，那么参数之间的相关性越大；相关系数越小，相关性越小。相较于其他参数而言，能量∅1、∅6这几个参数之间相关性较小，保持有良好的独立性，因此可以选取这一组参数来对肿瘤图像进行特征提取，以便更加准确全面地对肿瘤图像的纹理进行描述。

图11 相关系数折线图

4 结论

在医学领域中脑部肿瘤图像的分割对医生进行疾病的诊断与病理研究至关重要。本文应用K均值聚类算法对脑部MRI图像分割，检测并提取出脑部肿瘤图像，对所提取出的肿瘤进行纹理描述和特征分析。其中灰度共生矩阵可以精确地描述图像纹理的粗糙程度和重复方向；不变矩具有旋转不变性，是对图像的一种非常有效的形状描述子。本文结合灰度共生矩阵法与不变矩方法，分析灰度共生矩阵提取出了肿瘤图像及不变矩方法的参数，提取出三个相关性较低的参数，在减少特征维数的同时既保留了灰度共生矩阵描述的图像纹理特征又体现了不变矩描述的图像的几何特征，同时降低了算法的计算量，提高系统的鲁棒性。未来研究中，可综合多种特征提取方法所得参数，提取出具有维度低、信息更加丰富的特征，应用于图像的分割中，来满足实际临床需要。