火星车避障相机光学设计

曹 振,张永久,叶 葳,赵晓雨

(1.北京控制工程研究所,北京 100190；2.华北光电技术研究所,北京 100015)

1 引 言

火星巡视探测任务中的火星车需配备多种用于功能实现和科学探测的相机。其中,避障相机位于火星车底部,用于较近距离(<5 m)的地形观测并提供自动导航和避障所需的图像数据[1]。火星车的前后端各搭载一对避障相机,用于实现任意行进方向上的障碍物探测。根据自动导航和避障的要求,避障相机需工作在可见光波段(600～800 nm),其视场应接近半球。避障相机实际上是一个极大视场的鱼眼镜头,把半球投射到平面上会不可避免的产生筒形畸变,所以相机不能实现传统f-θ物像关系下的畸变校正。桶形畸变的引入实现了半球立体角范围的视场覆盖,相应的避障相机需满足f-θ物像关系即像高y′与物方光线入射角度θ成正比[2]。避障相机具有较短的焦距以匹配CCD尺寸。为了获得较为均匀的像面照度,光学设计需要合理控制像面入射光线的角度。

在满足光学性能要求的同时,避障相机设计还必需考虑以下约束条件:①小型化、轻量化；②采用的光学玻璃具有一定抗辐照性；③避免使用非球面光学元件；④避免使用胶合元件(火星低温环境会对胶合面造成影响)；⑤相机结构具有良好的可制造性。

为了实现相机光学系统的小型化、轻量化、高透过率的设计要求,光学系统应采用尽可能少的镜片。在三片式鱼眼物镜初始结构的基础上,增加一片正透镜来降低像面上光线入射角度,以获得较好的像面照度一致性。在避障相机优化过程中将光学系统将“形态参数”作为约束条件以推动停滞的优化过程[3]。最终,利用 4片分离的球面透镜结构,实现了接近衍射分辨极限的成像质量且像面上光线入射角度得到有效控制。在此基础上,以MTF为像质评价指标,分析了避障相机的制造公差。分析结果表明,当最严间隔公差、偏心公差在±0.02 mm范围内,最严倾斜公差在±1′范围内时,相机在30 lp/mm下的MTF在97.7 %的置信概率下大于40 %。设计的火星车避障相机满足成像性能的要求且具有良好的可制造性。

2 性能要求和设计约束

火星车避障相机用于较近距离地形地貌的观测,配合火星车其他相机实现避障和自动导航。避障相机光学系统需要满足以下基本光学特性要求:

2.1 成像视场

一对避障相机固定在火星车底部,相机为广角光学系统。根据探测需求,避障相机的物方视场角为124°×124°,对角线视场角2ω为180°。

2.2 F数

避障相机应在0.2 m～∞的物距范围内均能够清晰成像。当光学系统的对准平面位置为无穷远时,系统得到最大的景深。这时,从近景平面的位置P/2到无穷远的空间都能清晰成像[4]。

(1)

其中,z′为光学系统允许的弥散斑直径,f′为光学系统的有效焦距。为了满足CCD尺寸、成像视场以及景深要求,相机的焦距设为4.8 mm,F数设为15。

3 畸 变

避障相机需满足f-θ物像关系,即像高y′与物方光线入射角度θ成正比。相机在f-θ物像关系下的相对畸变应小于0.25 %。

3.1 像方主光线入射角

为了实现像面照度的一致性,应尽可能降低边缘视场在像面上的光线入射角度。此外,相机在像面处的主光线入射角还需要和CCD的光线入射角响应曲线相符合。

为了实现要求的功能,确定了避障相机的光学性能指标,如表1所示。

表1 避障相机设计指标要求

在实现上述光学特性的同时,避障相机的设计还需要考虑可制造性以及环境适应性。因此,避障相机具有以下设计约束:1.采用可能少的镜片,在减轻镜头的重量的同时,保证较高的透过率。2.避免采用胶合透镜,火星上低温可达-120 ℃,粘接胶在如此苛刻的条件下容易开裂。3.避免使用非球面光学元件,非球面的加工难度高,环境温度变化所引起的面形变化对严重影响成像质量。4.光学结构应具有良好的可制造性,具有较为宽松的制造公差。

4 光学设计

4.1 初始结构

避障相机设计首先要选择合适的初始结构。分离的三片式鱼眼物镜结构能够基本满足相机成像视场和相对孔径的要求。避障相机的初始结构如图1所示,由于要求的视场较大且三片式鱼眼物镜结构的优化自由度有限,因此初始结构的像差没有得到很好校正。另一方面,初始结构的像方光线入射角度没有得到很好控制,不能满足像面照度均匀性的要求。为了增加优化自由度同时合理控制像面上光线入射角度,需要在光学系统适当的位置增加透镜。此外,在镜头结构优化设计过程中,还需加入各类可制造性约束条件。

图1 三片式初始结构图

4.2 优化设计

4.2.1 镜头形态参数

J.M.Sasian和M.R.Descour提出了镜头性参数W和S[5]。镜头形态参数的构造基于近轴光线追迹,其不依赖于光学系统的孔径、尺寸、共轭条件以及视场角。其中,形态参数W反映光学系统中各光学面光角度的分布情况,其定义为:

(2)

其中,N为系统中光学表面的数目;wj为表面j的归一化光焦度:

(3)

另外一个形态参数S反映光学系统中各光学表面的“对称性”(“对称性”体现光学表面与光阑中心的同心程度或满足齐明条件的程度),其定义为:

(4)

其中,sj表示为:

(5)

通过对大量光学系统进行形态参数计算发现,具有较小W和S值的光学系统,通常具有较好的像差平衡性质和提供良好成像性能的潜力[6-7]。上述性质和潜力也是对避障相机的设计要求。

4.2.2 优化策略

避障相机初始结构的像方光线入射角度没有得到很好控制,不能满足像面照度均匀性的要求。另一方面,三片式结构的优化自由度有限,初始结构的相差没有得到很好的校正。为了合理控制像面上光线入射角度同时实现良好像差校正,需要在初始结构合适的位置增加透镜。根据4.2.1节所述具有较小W和S值的光学系统,通常具有较好的像差平衡性质和提供良好成像质量的潜力。因此,当初始结构需要增加透镜时,该透镜的引入应当使系统当前的形态参数得到最有效的减小[8]。

根据wj定义,其满足:

(6)

理想情况下,当所有光学面的wj相等时W取得最小值,即系统光焦度在各个表面均匀分布。而实际情况是为了满足光学特性和成像质量的要求,各光学面的wj数值有大有小,也有正有负。wj绝对值越大则该面对总光焦度的贡献越大,通常情况下其引入的高阶像差也越大。因此,为了降低W值、改善系统中各光学表面光焦度分布均匀性,应当在wj值最大的表面处插入新元件,以期分担该表面对总光焦度的贡献。

根据以上讨论,确定避障相机的优化策略为:在指定的表面位置处(wj或sj值最大的表面)插入“薄弯月”透镜。“薄弯月”透镜的曲率半径与指定表面的曲率半径相同。在进一步的优化过中,逐步增加“薄弯月”的厚度及其与参考表面的距离,同时将物方镜组的光学特性要求以及形态参数S和W作为优化的约束条件,以保证最终系统在满足光学特性要求的同时兼备良好的像差校正潜力。

在优化过程中还需控制各类可制造性约束条件,具体包括,空气间隔、镜片中心厚度、镜片边缘厚度、透镜两表面球心距离、像面主光线入射角度等。当评价函数不再持续收敛、陷入局部最小值时,把镜头的形态参数W和S做为罚函数加入评价函数继续进行优化,以推动停滞的优化过程。应用上述设计方法得到避障相机结构如图2所示。系统的W值由初始的4.85下降到1.17,而S值由初始的2.23下降到1.69。优化后获得了较为理想的成像质量,避障相机的具体性能分析见4.3节。

图2 避障相机结构图

4.3 性能分析

设计的避障相机的F数为15,在±90°视场(圆视场)内,全视场RMS波像差的平均值为0.029λ,最大值为0.036λ,如图3所示。

图3 避障相机波像差

避障相机的光学调制传递函数(MTF)贴近衍射分辨极限(如图4所示),在30 lp/mm处的MTF值大于45 %。

图4 避障相机调制传递函数

相机的畸变如图5所示,全视场主光线相对畸变小于0.2 %。

图5 避障相机的畸变

5 公差分析

为了实现避障相机的预期性能同时保证其具有良好的可制造性,需合理分配各项公差[9]。为简化机械结构、保证高可靠性,避障相机仅采用像距作为可调节的结构参数。使用光学设计软件CODE V,以30 lp/mm处的MTF≥0.4为评价标准对镜头进行公差分析。±90°视场范围内7个视场点(F1～F7等分)的波像差累积概率分布如图6所示,各视场MTF以97.7 %的概率下大于0.4。在上述像质标准下,相机光学系统的制造公差如表2所示。公差分析结果表明,光学系统最严间隔公差和偏心公差为±0.02 mm,最严倾斜公差为1′,透镜最严面形误差(局部光圈)为0.3。现有光学系统加工和装调精度完全能够满足镜头的制造公差要求。

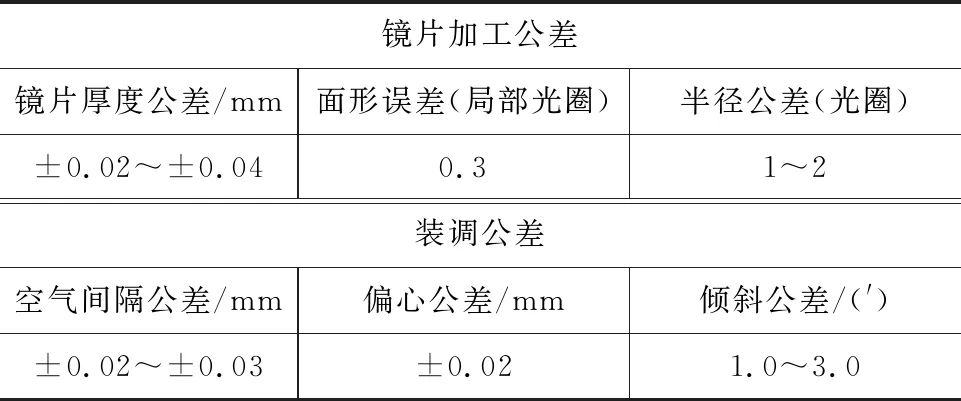
表2 制造公差

6 结 论

详细论述了火星车避障相机的设计要求和约束条件。在三片式鱼眼物镜初始结构之上,通过额外引入透镜增加系统优化自由度,同时有效降低了像面上光线入射角度。相机光学系统在优化过程中约束了镜头的形态参数,在不增加设计自由度的情况下,获了全局最优解。光学系统仅使用了4枚球面镜和1枚滤光片,实现了接近衍射分辨极限的成像质量和相机的轻量化设计。在此基础上,分析了相机光学系统的制造公差为评估其制造难度提供了依据。设计的避障相机能够满足火星车避障和近距离地形探测的需求。