具有跳跃项的Duffing方程的拟周期解❋

张新丽

(1.中国海洋大学数学科学学院， 山东 青岛 266100; 2.青岛科技大学数理学院， 山东 青岛 266061)

0 引言

近年来，具有跳跃项的半线性Duffing 方程

x″+ax+-bx-=f(x,t)

(1)

已成为非线性振动理论研究的热点(见文献[1-10])，其中a和b是正常数，且a≠b；x+=max{x,0}，x-=max{-x,0}，当方程中f(x,t)只与t有关时，方程(1)变为

x″+ax+-bx-=f(t)。

(2)

Dancer[1]和Fucik[2]研究了方程(2)的边值问题。Ortega[3]研究了方程

x″+ax+-bx-=1+εh(t)。

(3)

他证明了当|ε|充分小，h(t)∈C4(R/2πZ)时，一切解是有界的，即对于任意t∈R，解x(t)

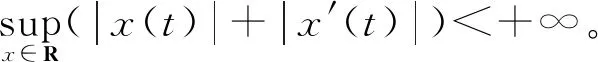
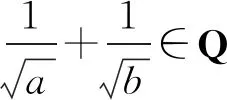
Liu[7]将方程(2)中f(t)是周期情形的结果推广到了拟周期情形。他首先建立了拟周期反转映射的不变曲线的存在性定理，并利用它证明了当f(t)是实解析拟周期函数时，方程(2)拟周期解的存在性和任意解的有界性。

文献[8]建立了光滑拟周期映射的不变曲线的存在性定理，并证明了当f(t)是光滑拟周期函数时，方程(2)的拟周期解的存在性和任意解的有界性。

Wang[9]研究了方程(1)中函数f(x,t)=p(t)-φ(x)的情况，其中p(t)为光滑的2π周期函数，扰动项φ(x)为有界函数，利用Ortega建立的扭转定理，证明了周期解的有界性。

文献[10]研究了方程

x″+ax+-bx-=Gx(x,t)+p(t)。

(4)

式中：p(t)∈C23(R/2πZ)；G(x,t)∈C21(R×R/2πZ)，利用Moser 小扭转定理证明了方程任意解的有界性。

受文献[8-9]启发，本文研究方程

x″+ax+-bx-+φ(x)=p(t)。

(5)

式中：扰动项φ(x)为有界函数，且φ(0)=0；p(t)是光滑拟周期函数，其频率ω=(ω1，ω2，…，ωn)满足Diophantine条件

(6)

式中：|k|=|k1|+|k2|+…+|kn|；常数σ0；μ>0。利用文献[8]中的扭转定理，证明了方程(5)的拟周期解的存在性和任意解的有界性。

先引入辅助函数[4]

C(t)是初值问题

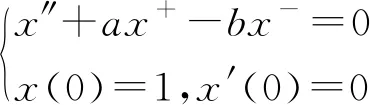
的解。记S(t)=-C′(t)，则

(Ⅰ)C(-t)=C(t),S(-t)=-S(t)。

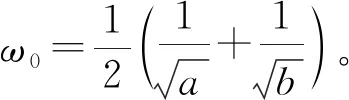
(Ⅲ)S2(t)+a(C+(t))2+b(C-(t))2≡a。

本文的主要结果如下：

定理1设对任意的k∈Zn{0}有〈k,ωω0〉∉Z，若(H1)p(t)∈Cq+1(q>2n+1)，且

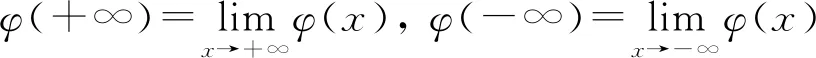
(H3)bφ(+∞)-aφ(-∞)≠p0(b-a)。

则方程(5)有无穷多个拟周期解，且所有解是有界的。

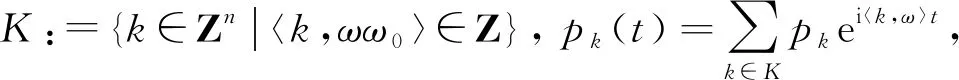
(H4)p(t)∈Cq+1(q>2n+3)，且

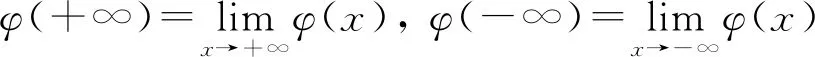
则方程(5)有无穷多个拟周期解，且所有解是有界的。

在下文中，规定c<1和C>1是两个通用的正常数。

1 准备工作

方程(5)等价于下面的非自治Hamilton系统

(7)

其中

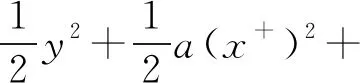
容易证明下面的引理：

引理1对任意(x0,y0)∈R2,t0∈R，哈密顿系统(7)在整个t轴上存在满足z(t0)=(x0,y0)的解为z(t)=(x(t;t0,x0,y0),y(t;t0,x0,y0))。

利用变换

(8)

其中

(9)

(10)

由φ(x)∈Cq(R),p(t)∈Cq+1(R/2πZ)知，I1,I2关于r,θ分别为Cq+1,C2。记

(11)

有如下结论(见文献[4])：

(12)

(Ⅱ)

(13)

(Ⅲ)若函数

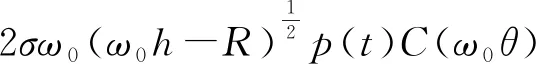
(14)

(15)

(Ⅳ)若假设

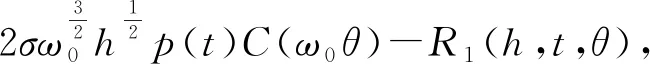
(16)

其中

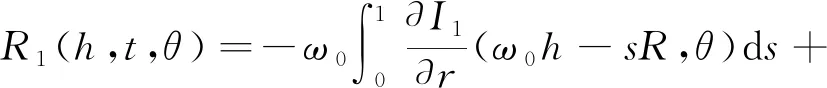
(17)

则

(18)

(Ⅴ)

(19)

(20)

(Ⅶ)令

(21)

(22)

下面对哈密顿系统(8)做正则变换。系统(8)的Hamilton函数h(r,θ,t)由(9)式给出。由于

rdθ-hdt=-(hdt-rdθ)，

这意味着若从(9)式能解出r=r(h,t,θ)作为h,t和θ的函数，于是

(23)

方程(23)是一个Hamilton系统，它以r=r(h,t,θ)为其Hamilton函数，以h,t和θ分别作为作用变量、角变量和时间变量。由(9)知

且当r>>1时，

(24)

由隐函数定理知，存在函数R=R(h,t,θ)，使得

r(h,t,θ)=ω0h-R(h,t,θ)，

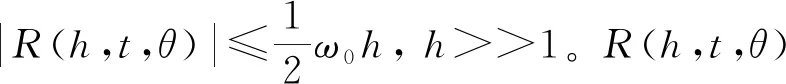
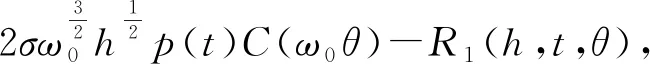
(25)

其中R1(h,t,θ)满足(18)。因此系统(8)转化为

(26)

引理2[9]存在正则变换Φ1：h=ρ,t=τ+T(ρ,θ)，其中T(ρ,θ+2π)=T(ρ,θ)。在此变换下，Hamilton函数(25)变换为

(27)

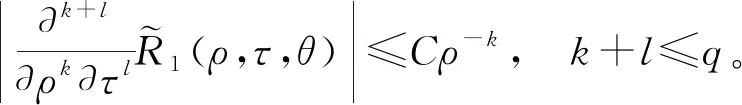
2 定理的证明

本节利用文献[8]中的小扭转定理来证明2个定理。考虑正则变换后的Hamilton系统

(28)

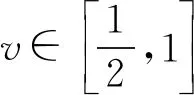
(29)

显然，系统(28)变换为

(30)

其中

由(21)知

(31)

将J(ω0δ-2v)代入Hamilton函数H(v,τ,θ,δ)，得

其中

由注释(Ⅶ)和引理2得到

(32)

新的Hamilton函数H(v,τ,θ,δ)代入系统(29)得到

(33)

在初始条件(v(v0,τ0,0),τ(v0,τ0,0))=(v0,τ0)下，系统(33)存在解(v(v0,τ0,θ),τ(v0,τ0,θ))，可设它有如下表达式

(34)

因此系统(33)的Poincare映射P1为

P1(v0,τ0)=(v0+δF2(v0,τ0,θ),τ0+ω0θ+

δF1(v0,τ0,θ))。

对(34)两边求导得

(35)

由式(32)和(35)可得，当δ→0+,k+l≤q-2,时，

其中C0是与δ无关的常数。此时记作

F1(v0,τ0,θ)=Oq-2(1),F2(v0,τ0,θ)=Oq-2(1)。

若当δ→0+，k+l≤q-2时

记作

F1(v0,τ0,θ)=oq-2(1),F2(v0,τ0,θ)=oq-2(1)。

因此

v(v0,τ0,θ)=v0+δOq-2(1),
τ(v0,τ0,θ)=τ0+ω0θ+δOq-2(1)。

(36)

由式(35)直接计算知

F1(v0,τ0,2π)=

F2(v0,τ0,2π)=

故Poincare映射P1的表达式为：

(37)

其中

(38)

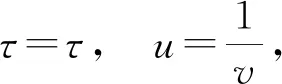
(39)

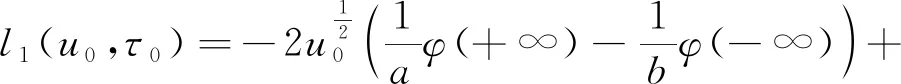
(40)

假设函数p(t)具有如下Fourier展开式

定理1的证明：若对任意的k∈Zn{0}有〈k,ωω0〉∉Z，由文献[8]中的定理3.1知，若δ充分小且

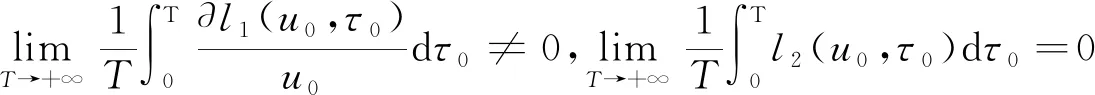
即bφ(+∞)-aφ(-∞)≠p0(b-a)；

由式(8)及Fubini定理知

满足文献[8]中定理3.1的所有条件，因此系统(33)的Poincare映射有拟周期不变曲线，频率为(ω1，ω2，…，ωn)。从而系统(7)有无穷多个拟周期解，且所有解都是有界的。定理证毕。

注1：从定理1的证明过程知，系统(7)有无穷多个频率为

的拟周期解，其中α满足下面的条件

其中常数γ，δ充分小，

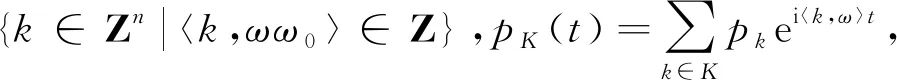
根据文献[8]中定理3.4证明过程知，

l=l1(u0,τ0),m=l2(u0,τ0)，

由于∀τ0∈R，

不妨设

令

则

满足了文献[8]中定理3.4的所有条件，因此系统(33)的Poincare映射有拟周期不变曲线，频率为(ω1，ω2，…，ωn)。因此系统(7)有无穷多个拟周期解，且所有解都是有界的。定理证毕。

注2：从定理2的证明过程知，系统(7)有无穷多个拟周期解，其频率为

其中α满足下面的条件

α∈[Ω(1)+12-3γ,Ω(2)-12-3γ],

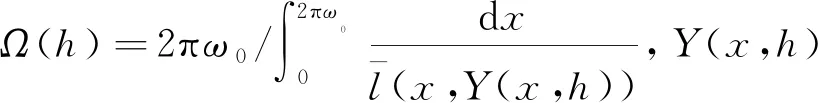
致谢:本文的研究和写作过程中，朴大雄教授给予了悉心地指导，并提出了很多宝贵意见，作者在此向他表示诚挚的谢意。