一种混合模型的时序数据异常检测方法
温粉莲
(中国移动通信集团广东有限公司,广州 510623)
0 引言
随着移动通信的发展,云计算、大数据、虚拟化等技术的大量应用,业务系统和网络架构变得越来越复杂,给运维人员带来了更高的挑战。如何有效的管理和监控海量的数据来保障系统的稳定、减少宕机时间,是系统运营和运维成功与否的关键所在。通过自动化的采集、监控各类设备指标数据和用户行为数据,运维人员能有效的掌握系统运行状况,异常检测是有效发现系统潜在故障和用户异常行为的重要方法。Chandola[1]等人及Numenta[3]公司对异常检测方法进行了全面的调研,目前常用的异常检测方法有:
(1)固定阈值法:通常根据业务专家或者运维专家的经验知识设定阈值范围。该方法优点是简单,缺点是需要大量依赖人工经验,不适用于周期性变化的数据,维护困难。
(2)基于统计学方法:如累计和控制图(CUSUM)and指数加权移动平均法(EWMA)[1],这种方法的优点是效率比较高,缺点是需要预先定义时间窗口,准确性依赖于参数设置。
(3)基于机器学算法:E.Keogh[2]提出了检测时间序列中异常值的方法。异常检测在不同的领域也有不同的应用,M.Szmit[4]等人提出了异常检测在网络流量上的异常检测方法,宋海涛[5,6]等人也提出了用户异常行为的检测。当前流行的异常检测算法有:基于分类,基于聚类,基于最近邻,基于信息理论,这些方法应用到不同领域的异常检测中,能有效提高检测的准确度。
本文设计了一种混合模型的时序数据异常检测算法,将历史数据按照时间进行划分,再用grubbs算法剔除历史数据中的异常点,得到不同时段的动态阈值,再使用曲线拟合和ARIMA对数据进行训练得到相应的模型。当对新指标进行异常判断时,首先通过动态阈值进行判异,如果输出为异常,则运用曲线拟合模型计算预测值,与判定值进行比较,如果输出为异常则进行第三层的判异,即使用ARIMA模型的预测值比较来判断异常。经过三层判断为异常的值经过确认后会以事件方式通知告警处理模块,被判断为正常的值则直接加入历史数据中。这种方法不仅提高了准确性,也提高了效率,无需事先进行人工标注,同时自动形成异常检测的闭环,对周期性、非周期性变化的指标数据都适用,具有很强的通用性。
1 方案设计
1.1 异常定义
本文将指标“异常”定义如下:当指标数据的变化偏离了该时间点的绝大多数数据分布范围并且不符合某种趋势变化的凸点或者凹点,认为是异常。
1.2 解决思路
该方法包含以下几个步骤:
(1)对历史的时间序列数据进行预处理和特征提取。
(2)利用K-means对数据初步的划分。
(3)使用Grubbs Test方法剔除每个划分后的孤立点,生成动态基线。
(4)使用曲线拟合法对历史数据进行训练,得到模型1。(5)使用ARIMA算法对历史数据进行训练,得到模型2。
(6)获取判断值,预处理后与该时刻的阈值进行比较,如果不在基线内,则判断为异常并进行第2层的判断,如果超过3个标准差,则判断为异常,再进行第3层的判断,三层判断均为异常的情况下,最终判断为异常,否则为正常。
异常检测系统的结构图如图1所示,该系统包含的核心模块包含:预处理、分类、模型训练、动态阈值生成、异常检测和异常处理。
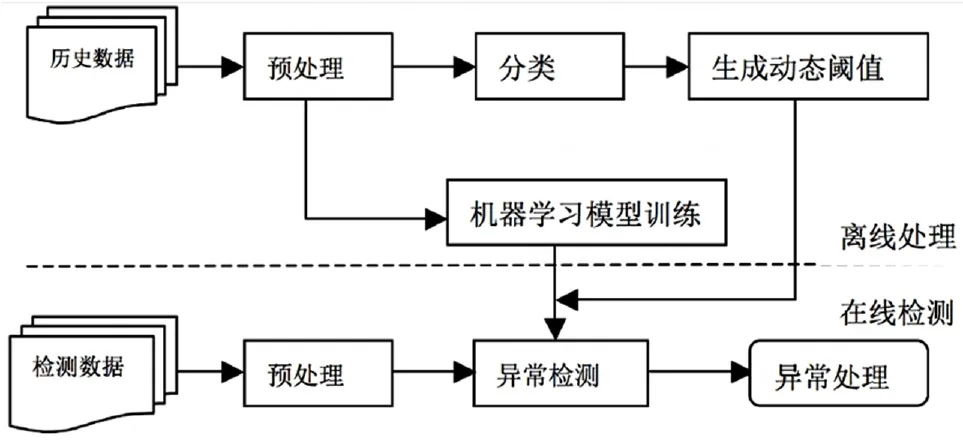
图1 指标数据异常检测系统框架
2 混合异常检测方法
2.1 预处理、特征提取和分类
假设某类指标数据的采集频率为d分钟一次,每天产生m个记录,使用n天的历史数据作为训练库,一共有n*m个记录作为历史数据。将这些数据的时间进行归一化处理,即去掉日期信息,只保留时、分、秒,再将时、分转换成小时,得到0-24之间的数值,经过归一化处理后,得到n个维度为m的向量。


经过预处理和特征提取后,我们可以运用聚类算法对数据进行划分,K-means是最常用的基于划分的方法,它的原理简单,计算代价小,聚类效果好,本文采用二分k-means算法来划分数,可以解决一般的k-means算法收敛于局部最小值的问题。
2.2 Grubbs方法生成动态阈值
采用格拉布斯方法,通常取置信概率为95%,其判别方法如下:先将呈正态分布的等精度多次测量的样本按从小到大排列,统计临界系数G(a,n)的值为G0,然后分别计算出G1、Gn:G1=(X-X1)/σ,Gn=(Xn-X)/σ (1) 若G1≥Gn且G1>G0,则X1应予以剔除;若Gn≥G1且Gn>G0,则Xn应予以剔除;若G1<G0且Gn<G0,则不存在“坏值”。然后用剩下的测量值重新计算平均值和标准偏差,还有G1、Gn和G0,重复上述步骤继续进行判断,依此类推。
通过上述的算法我们将历史数据中的异常值剔除,再计算剩下正常值中的最小、最大和平均值作为该聚类的阈值。
2.3 使用曲线拟合方法训练模型
曲线拟合是一种较常用的数据拟合方法,用来找到数据的规律和模式,系统运行产生的时间序列数据通常满足某种模式,使用曲线拟合来找到这种模式有利于异常判断和发现,本文的曲线拟合采用的是最小二乘法,它使用简单,高效,易于理解。
这里,假设样本点的分布不为直线,我们可用多项式曲线拟合,即拟合曲线方程为n阶多项式[14]。
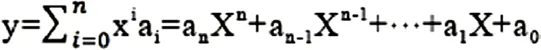
采用的是迭代法的梯度下降法求解,其中目标公式定义如下:
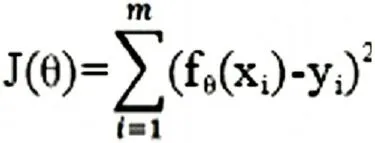
采用随机梯度下降的方法对参数向量求导,使得梯度为0,然后得到参数变量的迭代更新公式。实际实现中,我们采用python的机器学习包numpy进行计算,得到模型。
2.4 使用ARIMA方法训练模型
由于时间序列具有非线性、非平稳化、快速变化并且包含噪声干扰的特点,许多学者对时间序列进行了深入研究,提出了不同的预测模型。本文采用ARIMA算法进行模型的训练。
算法步骤包括:
(1)对时序数据进行平稳化处理,可选的有:移动平均法,加权移动平均法,对数处理,差分处理,分解处理。
(2)在设定最大的AR延迟数max_ar和最大的MA延迟数max_ma后,通过BIC准则进行模型的定阶,本文采用的是python的arma_order_select_ic进行自动定阶,确定p,q值。
(3)对平滑处理后的模型进行训练得到拟合参数。
(4)对模型进行还原处理得到模型。
将检测点时间作为上述ARIMA模型的变量计算上述两个模型的预测值,
∆2=|ρ2-y2|,其中,∆2是根据ARIMA模型计算出来的残差,如果∆2>2σ2,则判断为异常,σ2为近期时序数据的标准差。
3 实验与分析
3.1 效果评估
本文采用的混合模型算法的第一步是对指标进行粗略的划分,其中,访问量的变化是呈一定规律的,划分为4类,数据库的活动会话数值在统计区间变化很小,大部分的数据集中在20以下,因此只是分为2类,内存数值和CPU数值随业务变化不大,都被分为3类。第二步,对划分后的数据应用grubbs算法剔除异常值,计算正常数值集的最大、最小值,得到每一划分后的阈值。
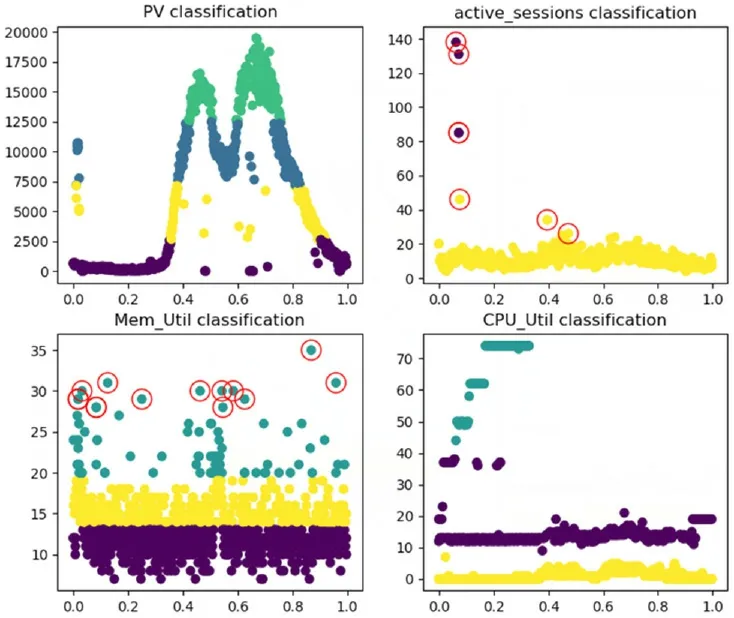
图2 使用KMeans结合grubbs算法进行划分并剔除异常
3.2 性能评估
本地测试所使用的硬件环境为一台i5-6200U 2.3GHz,内存:16GB,64位操作系统,Windows7版本,使用的语言是Python3.6.
3.2.1 时间序列算法性能
在本实验中使用的训练数据是1个半月的指标数据,采集粒度为5分钟,一共12,683条数据,训练数据10,139条,占总数据的比例为80%,预测数据占总数据的比例为20%,如果预测值与实际值之差超过3个标准差,则认为是异常。
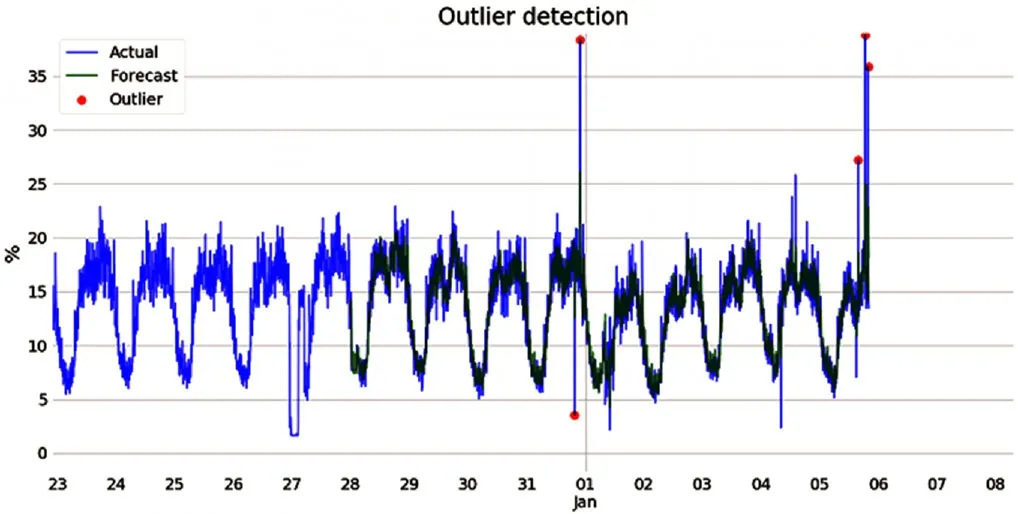
图3 使用ARIMA算法检测异常
从图3可以看到,在相对平稳的时间序列使用ARIMA算法预测可以得到比较准确的判断结果。
4 结束语
通信设备商在实际的系统运维过程中,会对多项用户指标数据和设备指标数据进行监控以便及时发现潜在的故障和缺数问题,目前的问题是:系统网络架构复杂多样,涉及的指标多,使用固定阈值会导致漏告、错告等问题,为了减少无效告警,提高告警准确率,本文设计了一套混合模型的时间序列指标异常检测算法,将历史数据按实际分布进行粗略的聚类,再使用Grubbs算法剔除聚类后的各数据集的异常值,得到动态的阈值基线作为初步判断的依据,接下来使用曲线拟合和ARIMA算法对近期的历史数据(t-5t时间窗口内的数据)进行训练,用来预测下一窗口的值(5t-6t),如果预测值与实际值的差值超过设定的阈值则产生一个事件,发送给告警处理模块进行告警处理,确认为异常的值会使用预测值填入历史数据,通过不停的迭代,剔除了异常数据,确保了训练数据的准确性。混合模型的异常检测算法结合了统计学算法的高性能,曲线拟合对某一类数据的准确拟合,及ARIMA算法的自动拟合的优点,兼顾性能和准确性,能很好的对不同趋势的数据进行预测和遗产检测。本算法在真实系统运维场景中使用的结果表明,查全率可以达到100%,平均差准率可以达到95.7%,算法的性能满足系统要求,通过运用算法将某系统的告警从每天754条压缩到40条,有效地压缩了无效告警,提高了问题发现率。

