基于归并策略的一致性时钟同步算法
范纯龙,孙强龙,刘海港
(1.沈阳航空航天大学计算机学院,沈阳 110136;2.沈阳飞机设计研究所,沈阳 110035)
0 引言
随着系统日益庞大复杂,分布化程度越来越高,诸多领域对网络各个节点的实时性和确定性有了更高要求。对于不同的应用场合,时钟同步的精确度需求有所不同。在工业领域,传感器的时钟同步精度一般要求在ms甚至μs级别;而在航空航天领域,其大规模信息化系统所要求的时间同步精度要求在μs甚至ns级别;而在一些精密仪器高频测试领域,时钟同步精度达到ns级别。
本文从时钟同步本质需求出发,在深入研究SPAD逻辑时钟模型与MTS算法的优缺点。在时钟拟合的过程中上引入归并策略,优化时钟迭代过程中的调节因子σij。仿真结果也表明改进后的MTS算法的同步精度、收敛速度、稳定性都得到了显著提升。
1 时钟归并策略
在一个仿真节点群内,每个仿真节点需要测试与广播自身与群代表时钟延迟,以此得到一个有序的群间时钟延迟序列T{T1,T2,T3,…,Tn}。如图1所示,提出两种组合策略。极大极小组合策略所产生的时钟组合在拟合虚拟时钟的过程中方差小,但通信代价大;而邻近组合则是方差大,通信代价小。时钟归并拟合的核心是通过少量的局部信息交换实现分布式一致性。
2 时钟拟合
2.1 时钟拟合
假定物理时钟是稳定的,可设计算机物理时钟的计时模型为:

中,Ti(t)表示仿真节点i的本地时间计时结果;ai表示节点i的计时速度;bi表示仿真节点i的初始偏移量。

图1 组合与归并
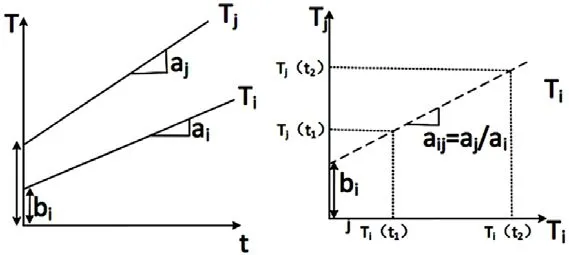
图2 时钟拟合过程
定义拟合的逻辑时钟的数学模型:
如图2右边所示,相邻的两个本地时钟所拟合的逻辑时钟模型依旧是线性的。我们期望将所有的仿真节点的本地时钟信息,都包含至一个虚拟的线性逻辑时钟模型中。在此,定义该时钟为Tv(t),数学模型为:

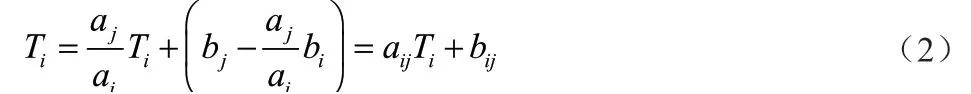
式中,av为最终虚拟时钟频率;bv为虚拟时钟的初始偏移量;t为本地时钟计数值。通过对本地时钟进行归并拟合,可以估算出参数av与bv。
根据式(2)以初步确定av与bv的计算方法,定义拟合时钟的递推计时模型:

式中,Tn表示时钟计数值,n=1,2,3,…表示步进次数;∆表示逻辑时间间隔;a表示时钟频率。
在时钟同步过程中,用σijn表示节点i的n次步进时相对于节点j的校准因子,是所归并的本地时钟差值与上一步进差值的比值,定义:

2.2 相对频率估计
节点i,j会在tn时刻以相同的频率互相发送存储各自本地时钟计数值Ti(tn)与Tj(tn),节点i会在下一步进估算自身相对于其邻居节点j的相对频率,记作定义相对频率估计的递推公式:

式中, 表示时钟迭代调控因子,主要作用一是降噪,二是使aij随时间自适应性自增长。
2.3 频率补偿
每个节点都会保存自己对全局变量的估计值,并通过相邻节点的估计值来更新自身,定义相对速率递推公式:

式中,avi,n-1表示节点i在n-1步进时对全局时钟速率的估计值;avj,n-1表示参考节点j在n-1步进时对全局时钟速率的拟合值。
2.4 偏移量补偿
当所有的时钟都完成对时钟速率的补偿,剩下的就是修复对时钟初始偏移量的误差,根据式(4)与式(5),定义初始偏移量的递推公式:
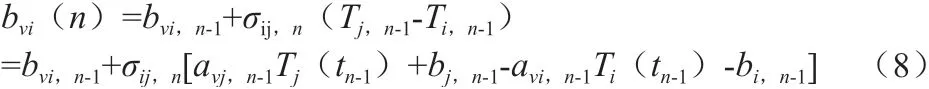
3 MTS算法
3.1 物理时钟模型
MTS算法的核心是通过邻近时钟两两归并,使所有仿真节点时钟频率快速收敛到全局虚拟时钟频率,以此实现全网时钟同步。因此时钟拟合过程的计算代价直接影响同步效果。由时钟拟合原理可知,每个仿真节点需要保存少量参数,计算代价小,在此给出MTS算法伪代码。
算法1 基于归并策略的一致性时钟同步算法

4 仿真实验分析
实验测试在Windows 7平台下,基于Matlab R2018a,采用Intel core i7-3770K 3.7GHz和8GB内存配置。考虑到在实际条件下难以达到测试的绝对同步性,即很难实现全部测试节点在相同的物理时刻进行时钟数据采样,本文采用仿真的方式对时间同步方法进行测试与分析。本次实验点仿真节点数量是10。仿真步长设定为0.001s,仿真步数设定为100。考虑到仿真节点的物理时钟频率的实际变动,确保仿真评估的可信性,选取的两组节点的本地时钟计时模型不尽相同,主要测试算法的收敛速度与每个节点逻辑计数值与级数均值的间隙大小。
实验结果如下:如图3与图4所示,各仿真节点的大约在17步时达到全网同步,与时钟计时均值的偏差也趋于0,算法收敛速度较快;且呈现出一旦同步,便不再失步,稳定性高。
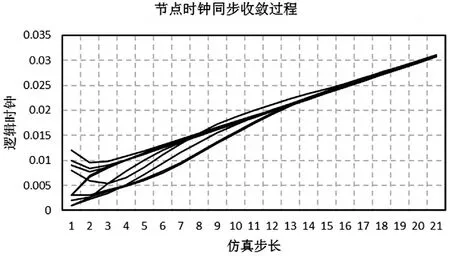
图3 Nodes-10仿真实验时钟收敛过程
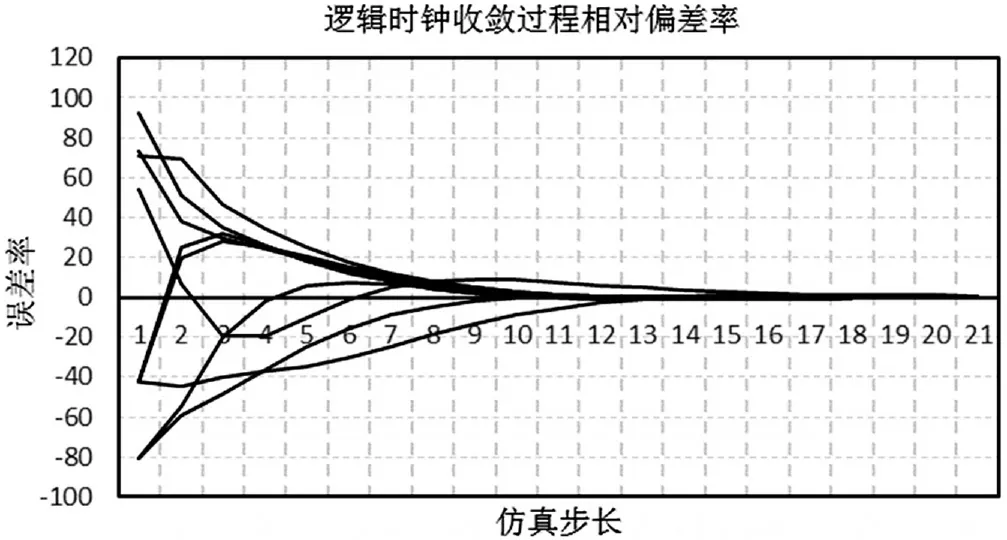
图4 Nodes-10仿真实验时钟误差率变化趋势
在相对稳定的分布式仿真网络中,MTS算法有着非常高的同步精度,而且其同步精度随着时间的增长呈现正相关趋势。在仿真实验过程中,30步进,时钟同步精度为10-15s,90至100步进时已经达到了10-31s同步精度。
图5反映MTS、SPAD、ATS算法仿真节点总数量对收敛速度的影响情况。纵坐标表示达到时钟同步所需的仿真步数,横坐标表示仿真节点数量。分别设定五组不同数量的仿真节点N:[5,10,20,50,100],不同仿真节点的时钟更新速度采样区间是[0.5,1.5],仿真周期0.001s。采用归并策略的MTS算法在不同仿真节点数量下,其收敛速度以及稳定度相比于ATS、SPAD都有很大的提升。
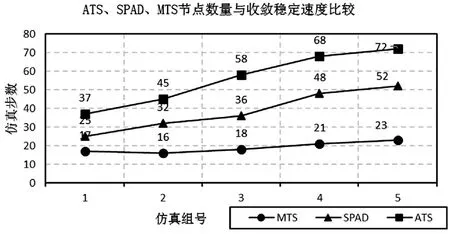
图5 不同算法仿真节点总量对收敛速度的影响
图6反映不同归并策略对算法收敛速度的影响情况。仿真节点数量为20,不同仿真节点的时钟更新速度采样区间是[0.5,1.5],仿真周期为0.001s。采用极大极小策略,时钟拟合最快,算法收敛速度快,其次是邻近策略。这两种相比于原算法在收敛速度方面皆有提升,但需要在这里指出的是,极大极小策略会有较高的延时成本,而邻近策略网络延时代价较低。

图6 不同归并策略下的MTS与ATS算法收敛速度影响
5 结束语
在ATS算法一致性同步的基础上,结合SPAD算法的参量差分逻辑时钟,并针对性地提出了一种基于归并策略的时钟同步算法(MTS)。MTS是一种集一致性同步、参量差分、逻辑时钟、归并策略等诸多方法于一体的算法。仿真实验表明,相较于原算法,MTS在同步精度、收敛速度、稳定性方面,都有提升。同时,本文也提出了分布式节点群同步策略的设想,其准确性也有待进一步的仿真实验验证。

