太阳帆航天器三维人工平动点变化特性研究
段 逊,岳晓奎,党朝辉
(1. 西北工业大学航天学院,西安 710072;2. 航天飞行动力学技术重点实验室,西安 710072)
0 引 言
太阳帆航天器是利用太阳光压作为动力实现轨道机动的航天器,可广泛用于各种深空探测任务,例如平动点探测[1-2]。虽然太阳帆航天器所获得的光压力量级比较小,但深空探测任务时间相对较长,其作用是不能忽略的。考虑太阳光压模型后,航天器轨道动力学会更加精确,可有效提高GPS卫星定轨、星际轨道转移和平动点附近周期轨道保持的精度。
平动点[3]又称为拉格朗日点,是航天器同时受到两个天体引力而相互平衡的位置,因其重要的动力学特性受到广泛的关注。将太阳帆航天器发送至平动点附近[4],可用作多种空间科学试验或天文观测的良好平台,目前美日等国家已开展或计划开展相关在轨验证任务。
美国航空航天局(NASA)于2010年11月发射NanoSail-D2[5]太阳帆航天器,成为第一个部署于近地轨道的太阳帆航天器,但其面积较小,仅有10 m2,所能提供的加速度有限。未来计划发射的Light Sail-2[6]太阳帆航天器,任务是维持航天器在日地系统L1平衡点附近的周期轨道上。
2010年,日本宇航局(JAXA)发射了Ikaros号太阳帆航天器[7],标志着第一个真正意义上的太阳帆航天器的诞生。其动力完全来源于太阳光压,并实现了飞掠金星的任务,具有标志性和里程碑意义。但整个任务过程中,并未考虑多体的情况。
最早利用太阳帆进行深空探测的概念是在1921年由前苏联学者Tsiolkovsky[8]提出的。而太阳光压模型最早是在1873年,由Maxwell提出的,后续Wie[9]、McInnes等[10]又对太阳光压模型进行了改进。在传统的限制性三体问题中,存在着五个平动点。而当添加太阳光压加速度后,则会导致平动点位置发生移动,从而形成一系列“人工”平动点。其中太阳光压加速度的大小主要受以下三个参数影响:光压因子以及太阳帆板与太阳方向之间的两个角度,锥角和钟角。光压因子主要受太阳帆板参数和面质比等参数影响。目前,国外的学者Farrés等[11]和Soldini等[12]研究了在不同坐标系下的平动点变化情况,但他们均忽略了钟角的影响,具有很大的局限性。国内学者龚胜平等[13],张青斌等[14],罗超等[15]研究了太阳帆航天器的轨道动力学和轨道控制研究,但均基于固定的平动点。侯锡云等[16]对太阳帆定点探测器在地—月系共线的平动点附近进行了研究,张辉[17]和朱敏[18]也进行了太阳帆影响下的平动点移动研究,不过只考虑了共线平动点在不同光压因子影响下的变化情况。
基于上述研究的不足,本文考虑了太阳帆航天器在光压因子、锥角和钟角三者共同作用下的五个平动点变化情况,从而得到了更加细致全面的五个三维“人工”平动点家族面。由于平动点的重要位置以及特殊意义,“人工”平动点可以为未来的科研任务提供更多的可能,包括提供新的周期轨道及日地流形选择等,更好地为未来太阳帆航天器在日地系统内的运动和平动点周期轨道等方面研究提供有效参考。
1 太阳帆航天器的动力学模型
太阳帆航天器在限制性三体模型下,只考虑两个主天体(地球和太阳)的力以及太阳帆产生的太阳光压力。假设两个主天体质量汇于质点,由于二者之间的互相吸引力,以圆形围绕其质量中心运行。同时,太阳帆航天器也被当成一个质点,它不影响两个主天体的运动,相反它受两个主天体的引力以及太阳帆的光压力影响。本文的模型为限制性三体模型加上太阳光压模型(CR3BP+SRP)。
本文采用旋转坐标系,中心原点位于太阳-地球的质量中心,X轴沿着连接两个天体的线,方向为从地球指向太阳,Z轴垂直于轨道平面,Y轴完成正交参考系。因此,在此旋转坐标系下,太阳的位置是X>0,而地球的位置是X<0。采用无量纲化,认为太阳和地球的质量之和为1,太阳地球距离为1,轨道周期是2π。在日地系统中,地球的质量是μ=3.00348060100486×10-6,1-μ对应的是太阳质量。图1为太阳帆航天器在日地限制性三体旋转坐标系中的示意图。
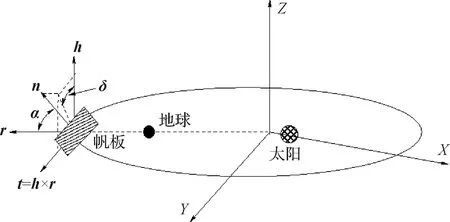
图1 太阳帆在日地系统下的示意图Fig.1 Schematic diagram of a solar sail under the Sun-Earth system
设(X,Y,Z)为太阳帆航天器在上述旋转坐标系中的位置,则其动力学模型可以写成:
(1)
式中:
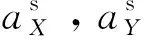
(2)

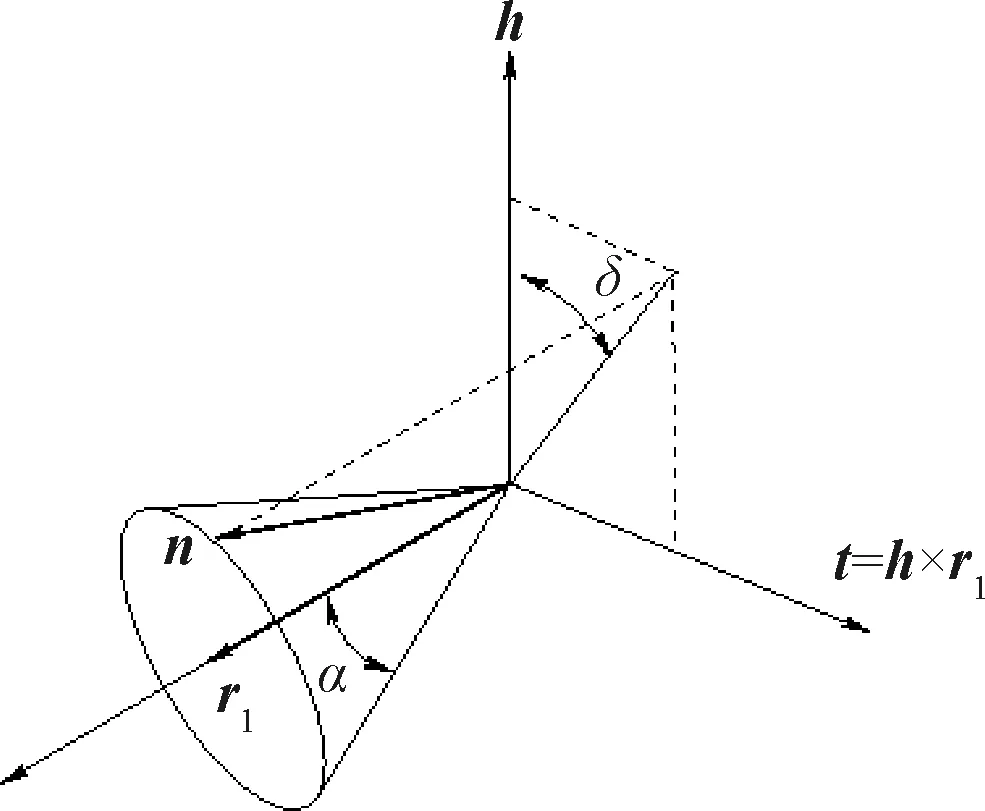
图2 太阳帆航天器角度示意图Fig.2 Schematic diagram of solar sail spacecraft’s angle
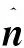
(3)



2 人工平动点的变化特性
平动点是在限制性三体问题中,受到天体引力与离心力互相平衡的位置,则在这些特殊位置下,探测器理论上速度和加速度均为零。满足:
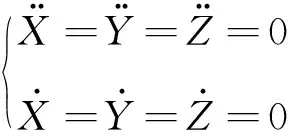
(4)
如果不考虑太阳光压的作用,传统限制性三体问题有五个平动点:有三个平动点在太阳和地球的连线上,且具有不稳定性。另外两个平动点在黄道面上,与两个主天体形成等边三角形[7],且是线性稳定的。图3为五个平动点在日地限制性三体坐标系下的示意图。表1给出了日地系统五个平动点的空间位置[12]。

图3 日地系统在CR3BP中平动点分布图Fig.3 The Sun-Earth system libration points distributionmap in CR3BP
表1 日地系统平动点位置
Table 1 The liberation points position in the Sun-Earth system
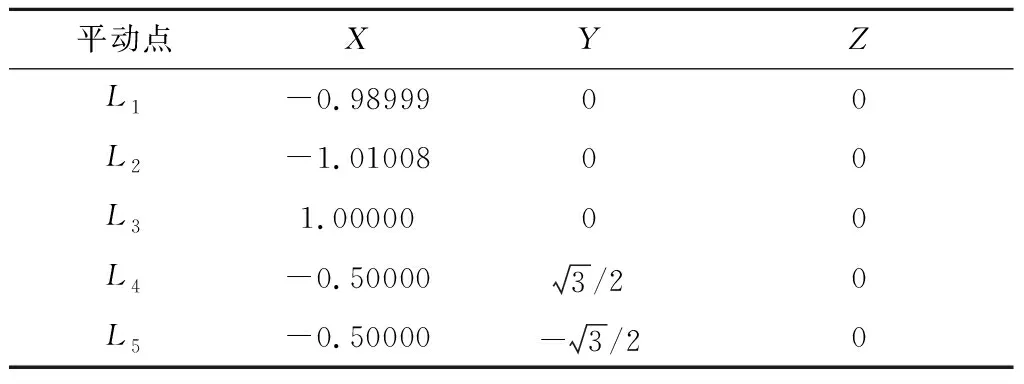
平动点XYZL1-0.9899900L2-1.0100800L31.0000000L4-0.500003/20L5-0.50000-3/20
若太阳帆航天器受到太阳光压的作用,则平动点位置发生改变,新形成的平动点分别记为:SL1,SL2,…,SL5。则在CR3BP-SRP模型下,平动点应满足下式:
(5)
对式(5)进行求解,则可得到新的“人工”平动点。本文在求解太阳帆航天器的“人工”平动点过程中,考虑了公式内的各个变量参数:包括光压因子(β∈(0,1)),锥角(α∈(-π/2,π/2))和钟角(δ∈(0,2π)),从而在不同的光压因子下,形成了以锥角和钟角为变量的3维平动点图。
2.1 “人工”平动点SL3,SL4和SL5的变化特性
当光压因子小于10-6的时候,改变钟角和锥角的大小,则会形成五个不相连的“人工”平动点家族面,如图4所示,其光压因子取值为7×10-7。图4中每一个点都对应着一个太阳帆角度。可以发现,其不再只是五个点,而是形成了五个面。随着光压因子增大,大于10-6的时候,“人工”平动点SL3,SL4和SL5开始相互靠近(如图5所示,此时光压因子为3×10-6)并最终融合,逐渐合并成了一个面,此时形成了三个不相连的平动点家族(即SL1和SL2各一个平面,SL3,SL4和SL5共形成一个面)。

图4 不相连的五个人工平动点(β=7×10-7)Fig.4 Five artificial libration points that are notconnected(β=7×10-7)

图5 逐渐靠近的人工平动点(β=3×10-6)Fig.5 The artificial libration points that areapproaching(β=3×10-6)
考虑SL3到SL5的“人工”平动点随着光压因子的扩大,相互融合成一个平面,且变化不大,故后续主要研究离地球最近的两个“人工”平动点(即SL1和SL2),也更加具有工程意义。
2.2 “人工”平动点SL1的变化特性
当光压因子小于0.03时,“人工”平动点SL1家族是一个封闭的球面,如图6所示。图6(a)、图6(b)分别是光压因子为0.01和0.02时的SL1家族“人工”平动点的情况。所选取的参考系及三轴范围是相同且固定的,图6(a)中,坐标轴内部的封闭球面为SL1三维“人工”平动点家族,而在XY平面内的图形为三维平动点对应的投影,便于观察其变化情况(图 6(b)及图7同理)。从图6可以看出,SL1点“人工”平动点家族随着光压因子增大,球面扩大。
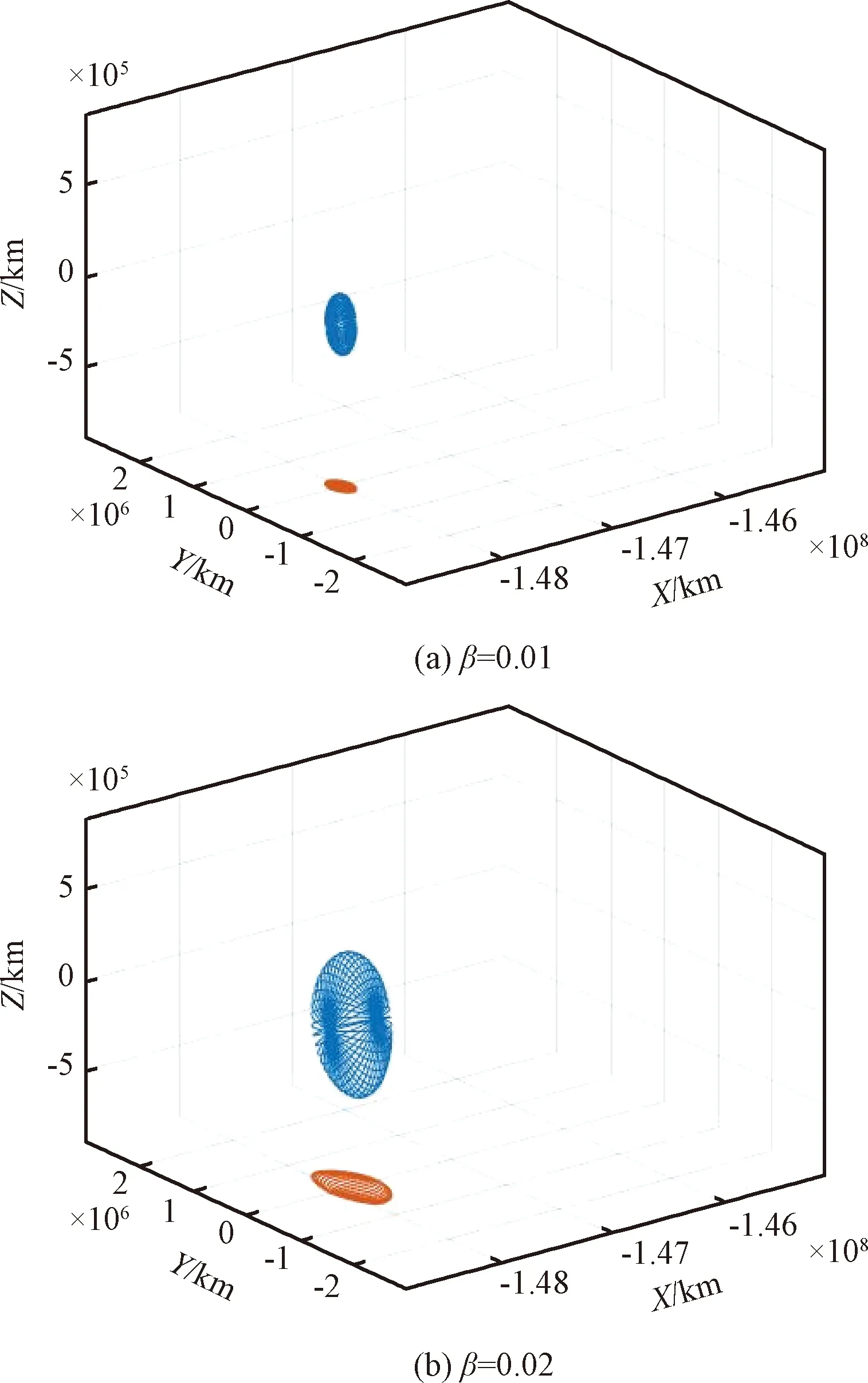
图6 SL1平动点(β<0.03)Fig.6 SL1 liberation points (β<0.03)
当光压因子大于0.03时,SL1家族“人工”平动点分裂成两个平面,而不再是一个封闭的球面。如图7所示。图7(a)、图7(b)分别是光压因子为0.03和0.05时的SL1家族“人工”平动点的情况。

图7 SL1平动点(β>0.03)Fig.7 SL1 liberation points (β>0.03)
针对SL1家族的“人工”平动点,从图6和图7可以得到:当光压因子为零的时候(即无太阳光压力的作用),其平动点是一个点。当存在太阳光压的作用下,SL1平动点会从一个点扩大至一个球面,并随着光压因子的增大,球面也随之扩大。直到光压因子扩大接近某个临界值(0.02~0.03),其会从一个封闭的球面分裂成两个平面(见图7(a)和图7(b)),右半部分随着光压因子的增大,向中心点方向移动,而左半部分会随着光压因子的增大,向地球方向缓慢移动,二者皆与SL3,SL4和SL5形成的平面融合在一起。此时系统内只有两个不相连的平动点面,一个是SL1,SL3,SL4和SL5合并组成的,另一个则是SL2单独形成的。
2.3 “人工”平动点SL2的变化特性
相比较“人工”平动点家族SL1的复杂,SL2家族的“人工”平动点,更加稳定,也更加直观,如图8所示。
图8中从里到外的光压因子,分别是0.01,0.05,0.09和0.13。从图8可以看出,SL2家族的“人工”平衡点,不会随着光压因子的变大而分裂,始终是一个封闭的球面,只是球面不断扩大。
2.4 “人工”平动点的变化特性小结
当锥角α=±π/2时,太阳帆板方向与日射方向垂直,则无太阳光压力,此时的模型则可简化为传统的限制性三体模型(SLi=Li,i=1,…,5)。
当锥角α=0的时候,太阳光垂直照射到太阳帆板上,即太阳帆板方向与入射光线平行。在这种情况下,太阳光压力与太阳的引力方向相反,所以可以理解成太阳的质量减少了。对应的SL1和SL2家族“人工”平动点会随着光压因子的增大,向太阳方向靠近运动。
若锥角取其他值,钟角δ=±π/2,则会产生一个在XY平面内的力,“人工”平动点也会对应着向左或向右移动。同理,若锥角δ=0°或δ=π,则会产生一个垂直于XY平面的力,“人工”平动点会向上或向下移动。
当锥角(α∈(-π/2,π/2))和钟角(δ∈(0,2π))各自单独变化,则会得到一个二维的“人工”平动点。若二者同时改变,会形成分析中所展示的三维情况。图4~图8中的每一个点均对应着一个确定的锥角和钟角。
当太阳光压(β∈(0,1))改变的时候,其各个平动点也会随之改变。当β<10-6时,则会有五个独立互不连接的平动点家族。当β>10-6时,SL3到SL5开始相互靠近并融合形成了一个大的平动点家族SL3~5。当β<0.02时,SL1始终保持着一个封闭的球面,此时有三个独立互不连接的平动点家族。当β>0.03,SL1会分裂成两个平面,且与SL3~5融合在一起,最终形成两个独立不连接的平动点家族。无论β如何变化,SL2“人工”平动点始终是封闭的曲面,只会随着β的增大而扩大球面。值得一提的是,“人工”平动点分裂后的左侧的SL1始终无法与SL2家族相融合。
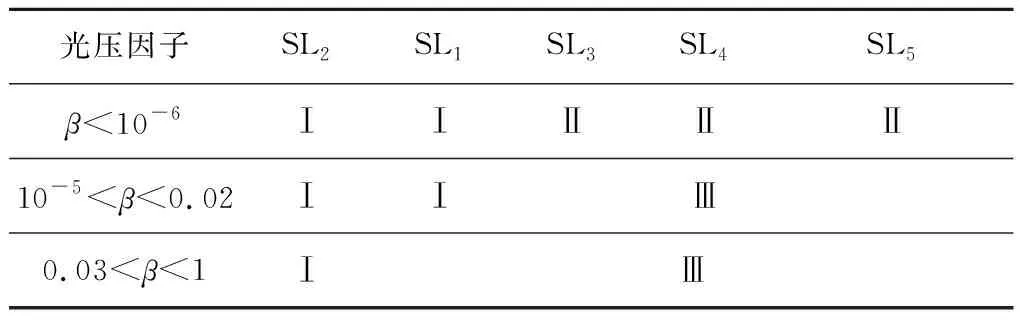
表2 平动点基于光压因子变化特性Table 2 Variation characteristics of liberation points based onsolar parameters
注.Ⅰ表示独立封闭不相连球面,Ⅱ表示独立不相连面,Ⅲ表示融合。
综上所述,平动点位置的改变,对应的周期轨道也随之改变,如图9所示。图9(a)为三维的图形,图9(b)为其XY平面投影。设置光压因子为0.02,当锥角等于0°,钟角为90°的时候,平动点和周期轨道为图9(a)和图9(b)的右侧部分。若锥角等于60°,钟角为90°时,则平动点和周期轨道更改为左侧部分。本文对航天器轨道设计的研究意义:1)周期轨道的保持,若航天器沿不稳定流形脱离原周期轨道,利用太阳帆角度的改变,使航天器沿着稳定流形进入新的周期轨道。2)规避地球阴影的影响,如图9所示。若右侧的周期轨道被阴影遮挡,则可以通过太阳帆转移至左侧的周期轨道上进行规避。3)由原先的五个平动点拓展成了平动点家族,为未来深空探测轨道设计提供了更多的可能性。

图9 平动点位置改变及Lissajous轨道Fig.9 The change of liberation points position andLissajous trajectory
3 结束语
本文针对太阳帆航天器受太阳光压作用会改变平动点位置的问题,研究了五个平动点在光压因子、锥角和钟角的影响下形成的三维人工平动点的变化情况。
本文讨论了在不同光压因子情况下的人工平动点SL1~SL5的变化情况。其中,考虑到SL2家族“人工”平动点不会随着光压因子β有巨大的改变,适合太阳帆航天器在此平动点进行周期轨道保持等研究,针对“人工”平动点SL1,SL3,SL4和SL5可以互相融合的特点,为未来的太阳帆航天器在日地系统内的转移提供了新思路。

