基于马尔科夫随机场的改进FCM图像分割算法

王 燕，亓祥惠，段亚西

兰州理工大学 计算机与通信学院，兰州730050

1 引言

图像分割是图像分析的预处理阶段[1]，就是将图像根据不同的属性分成不同的区域，从而为后续的图像分析做准备[2]。Dunn等提出模糊C均值算法（Fuzzy CMeans，FCM）。Bezdek首次将模糊聚类算法应用到图像分割领域[3]。Scherrer等人[4]利用马尔科夫随机场模型对局部强度进行估计，提高算法在处理磁共振（Magnetic Resonance，MR）图像时的抗噪性，但该算法没有考虑整体性，抗噪性提升不明显。Zhao等人[5]利用相邻子域关系提高对MR图像分割的抗噪性，但是应用于其他类型图像时，无法有效分割图像。Wang等人[6]将深度学习的先验信息作为马尔科夫模型的能量函数，但是无法有效处理背景复杂的图像。王少宇等人[7]提出一种条件随机场模型约束下的模糊C均值聚类算法（CRF-FC），利用先验概率对模糊聚类算法进行约束，有效提高算法的抗噪性，但处理背景复杂的图像时存在明显不足。Memon等人[8]提出一种改进的m维特征数据空间的模糊聚类算法（GKWFLICM），通过引入局部模糊因子提高算法的抗噪性，但无法有效分割灰度不均匀图像。

为了提高模糊聚类算法的抗噪性，本文提出一种基于马尔科夫随机场的改进FCM图像分割算法（Improved FCM image segmentation algorithm based on Markov Random Field，Kernel Function and Mahalanobis Distance，FKMFCM）。通过引入马尔科夫随机场先验概率，修正FCM算法的目标函数，提高算法的抗噪性。通过对比实验证明，本文提出的算法能有效提高模糊聚类算法的抗噪性。

2 FKMFCM算法

2.1 FCMKM算法

FCMKM算法将待分割图像像素点非线性映射到高维空间，然后将欧式距离替换为马氏距离，提高算法抗噪性。FCMKM算法目标函数如式（1）、式（2）、式（3）所示。对式（1）利用拉格朗日乘数法进行运算，求得隶属度迭代公式如式（4）所示，聚类中心迭代公式如式（5）所示。

式中，G为目标函数，uik为隶属度矩阵U的元素，vi为聚类中心V的元素，σ表示样本元素集X的标准差，m为模糊系数，c为聚类中心数目，n为样本个数，MK(xk,vi)表示样本元素集X的第k个元素到聚类中心集V的第i个聚类中心在高维空间的马氏距离，Σ表示样本元素集X与聚类中心集V之间的协方差矩阵。

2.2 马尔科夫随机场

马尔科夫随机场模型是统计学与图像处理相结合的产物[5]，利用该模型对图像进行先验概率求解，得到图像的联合分布概率[9]。为解决马尔科夫随机场实际应用问题，Geman等人[10]证明了吉布斯随机场与马尔科夫随机场的等效关系，Xie等人[11]给出了计算马尔科夫随机场的先验概率公式。

式中，h为标号场Ω的元素，U(h)为吉布斯能量，C为所有势团集合，Vc为势团势能。β为势团参数，通过β值来调节图像分割的细腻程度，取值范围是[0，1]，数值越小，图像分割越细腻。

2.3 初始聚类中心选取

为了提高FCM算法性能，将图像灰度值进行映射，得到灰度值变化折线图，将折线图局部极值作为聚类中心，局部极值的个数作为聚类数。

具体的计算步骤为：

（1）计算目标图像的灰度直方图，进一步得到灰度变化折线图；

（2）计算灰度变化折线图局部极值；

（3）将局部极值作为聚类中心，局部极值的个数作为聚类数。

2.4 评价指标

为防止主观评价因素的影响，现引入Bezdek划分系数[12]、Xie_Beni系数[13]、运行时间和迭代次数4个指标作为评测指标。

（1）Bezdek划分系数是分类模糊系数。分类越分明时，值越大，分类越模糊，值越小，计算公式如式（9）所示。

式中，c为聚类数目，n为样本数，uij为隶属度矩阵U的元素。

（2）Xie-Beni系数计算公式如式（10）所示。

式中，uij为隶属度矩阵U的元素，vi、vj、vk为聚类中心矩阵V的元素，xj为实验对象的元素。Xie-Beni系数越小聚类的内聚度越高，耦合度越低，分类效果越明显。

（3）运行时间是算法执行的时间，通过对比运行时间，可以清楚地比较算法的时间复杂度。

（4）迭代次数是指算法的迭代运行次数，通过计算迭代次数，可以有效地评价算法的收敛性。

2.5 FKMFCM算法

Ghosh等人[14]通过对FCM目标函数进行改进，添加修正项，如式（11）所示，提高模糊聚类算法的抗噪能力。

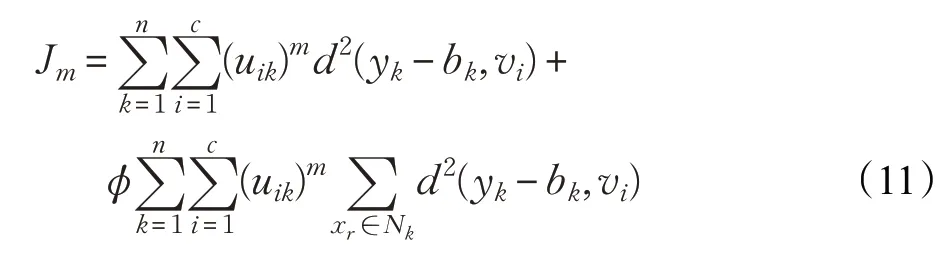
式中，m为模糊系数，ϕ为调整系数，n为样本数目，c为聚类中心数目，vi为聚类中心矩阵V的元素，y为样本矩阵，b为偏移场矩阵，uik为隶属度矩阵U的元素，d(yk-bk,vi)为yk去掉偏移场后与聚类中心vi之间的欧式距离。

FKMFCM算法将马尔科夫随机场先验概率作为目标函数的修正项，利用马尔科夫随机场模型描述像素间空间局部相关性，提高算法的抗噪性，改进的目标函数如式（12）所示。

式中，MK(xj,vi)表示第j个元素到第i个聚类中心在高维空间的马氏距离（如式（2）），λ为调整系数，P为马尔科夫随机场图像分割先验概率。根据拉格朗日乘数法，求得隶属度迭代公式如式（13）所示，聚类中心迭代公式如式（5）所示。

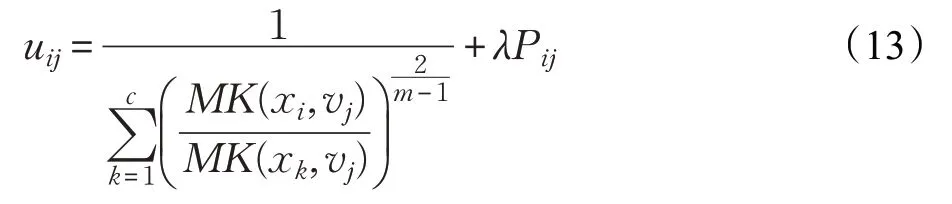
FKMFCM算法具体流程如下：

（1）通过初始聚类中心算法，求得聚类数目c和初始聚类中心V(0)，设定迭代终止阈值ε及迭代计数器b=0。

（2）更新隶属度矩阵U(b)，更新聚类中心矩阵

（3）根据得到的隶属度矩阵U(b)和聚类中心矩阵V(b)，计算标号场Ω，计算图像分割的先验概率，如果ε，则迭代终止，若未达到终止阈值或者迭代计数器未达到最大值，则重复步骤（2）和步骤（3）。

（4）迭代终止后，得到目标函数最小的最佳隶属度U和最佳聚类中心V。

（5）对于任意像素点xi，计算其对应的最佳隶属度矩阵Ui中元素的最大值uij，将uij对应的最佳聚类中心vj的灰度值作为像素点xi的灰度值。重复此过程，直至所有像素点灰度值都更新完毕，算法终止。

FKMFCM算法流程图如图1所示。

3 实验结果及分析

为验证本文提出算法的抗噪性，实验采用Berkeley图像库图像，并对传统FCM算法、GKWFLICM算法、CRF-FC算法进行抗噪性比较。实验环境为英特尔i5处理器，主频为2.6 GHz，8 GB内存，Windows 10系统的PC机，采用Matlab编译语言实现。

3.1 参数设置

为确定本文算法中调整系数λ的取值，对Berkeley图像库#15088图像进行实验，选取[0.1，1.1]之间的11个数作为实验数据，实验结果如图2所示。

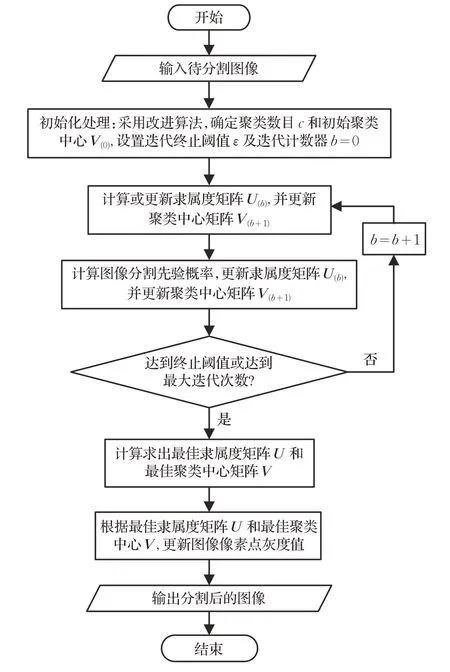
图1 FKMFCM算法流程图

图2 调整系数λ选取实验

对图2的分割效果进行分析，当λ=0.3和λ=0.5时算法得到较好的分割结果，因此图2（a）分割的最佳聚类中心为[51，84，90，171]，算法在λ=0.4时聚类中心为[51，84，151，171]，聚类中心产生了误差，致使FKMFCM算法的分割结果产生了波动。为确定最佳λ取值方案，对4个评价指标进行对比，结果如表1所示。

表1 调整系数λ取值实验结果表

从表1中可以看出，λ取值0.5与λ取值0.3相比，Bezdek划分系数较大，Xie-Beni系数较小，迭代次数与运行时间都有所减少。显然，λ取值0.5时的性能要优于λ取值0.3。综合分割效果与评价指标，调整系数λ取值0.5时，能有效提高算法的性能。

设置模糊系数m=2，势团参数β=1，迭代终止阈值ε=10-4，设置最大迭代次数为100次。

3.2 抗噪性能实验

对编号#41004（如图3）、#24063（如图4）图像进行算法抗噪性实验，分别添加高斯噪声和椒盐噪声，实验结果如图5、图6所示。

图3 #41004噪声实验图像

图4 #24063噪声实验图像

图5 #41004图像分割结果

图6 #24063图像分割结果

图5（a）分别为传统FCM算法、CRF-FC算法、GKWFLICM算法、FKMFCM算法处理原图像结果，图5（b）分别为四种算法处理高斯噪声图像的结果，图5（c）为四种算法处理椒盐噪声图像的结果。

FKMFCM算法能有效地将麋鹿的身体和角分割出来，且能做到目标边缘清晰，与未添加噪声的图像分割结果相近。其他三种分割算法虽然能将麋鹿的身体分割出来，但是都无法有效地将麋鹿的角分割出来，造成分割不完整，对于添加噪声的图像都无法有效地去除噪声。对四种算法处理原图像的结果进行评价指标对比，结果如表2所示。

表2 #41004图像分割实验评价指标对照表

从表2数据可以看出，相较于其他算法，FKMFCM算法Bezdek划分系数平均提高79.2%，Xie_Beni系数平均减少48.2%，迭代次数平均减少23.6次，运行时间平均减少4.6 s。FKMFCM算法能通过少量的迭代次数和运行时间，达到较好的图像分割结果。

图6（a）分别为传统FCM算法、CRF-FC算法、GKWFLICM算法、FKMFCM算法处理原图像的分割结果，图6（b）分别为四种算法对添加高斯噪声图像进行分割的结果，图6（c）分别为四种算法处理添加椒盐噪声后图像的分割结果。

传统FCM算法、CRF-FC算法能有效地将教堂分离出来，但是边界不清晰，GKWFLICM算法无法有效地分割教堂。对添加了噪声的图像，FKMFCM算法则能有效地屏蔽噪声干扰，将教堂分割出来，并且与原图像分割效果无明显差别，其他三种算法都无法有效处理噪声图像。从图中分割结果明显可以看出，FKMFCM算法能有效地处理添加噪声的图像。对四种算法处理原图像进行评价指标对比，对比结果如表3所示。

表3 #24063图像分割实验评价指标对照表

通过表3可以看出，相较于其他算法，FKMFCM算法利用更少的时间和迭代次数，得到最佳的聚类结果。Bezdek划分系数平均提高54.4%，Xie_Beni系数平均减少75.0%，迭代次数平均减少41.6次，运行时间平均减少6.17 s。通过算法抗噪性实验发现，FKMFCM算法能有效地提高模糊聚类算法的抗噪性，在处理添加噪声后图像时分割效果较好。

4 结束语

本文提出了一种基于马尔科夫随机场的改进FCM图像分割算法，即FKMFCM算法。利用马尔科夫随机场先验概率修正模糊聚类的目标函数，从而提高算法的抗噪性。通过对比实验发现，本文算法能有效地提高图像分割算法的抗噪性，但该算法也存在不足，算法采用单一固定变量调节先验概率，在处理医学图像时算法自适应性有一定缺陷。下一步的研究重点是动态调整λ的取值，提高算法在不同应用场景的抗噪性。