基于自适应步长果蝇优化算法图像分割

宋 杰，许 冰，杨淼中

安徽大学 计算机科学与技术学院，合肥230601

1 引言

果蝇优化算法（Fruit Fly Optimization Algorithm，FOA）是一种寻求全局优化的新方法[1]，它是根据果蝇寻食行为推理出来的。该算法因为可调参数较少，所以简单容易实现。而且果蝇在嗅觉与视觉等感官知觉上比其他物种敏锐，因此能够很好地搜寻到空气里漂浮的气味，甚至能嗅到40 km以外的食物源。靠近食物位置后能凭借视觉的敏锐度找到食物和同伴聚集的位置，然后朝目标源飞去。至今为止，已经有很多改进的果蝇优化算法，例如多样性种群果蝇优化算法[2]，利用强嗅觉果蝇，由正常果蝇突变为味道浓度判定值多样化的方法。基于模拟退火的果蝇优化算法（Fruit Fly Optimization Algorithm based on Simulated Annealing，SA-FOA）[3]，增大了接收概率，且利用非均匀变异因子改进步长。参数修正与收敛策略融合的果蝇优化算法[4]，为了解决味道浓度判定值不能是负数的问题，对味道浓度公式进行了修正；为了避免高维函数维间互扰问题，迭代优化的过程中对果蝇个体在最优值附近寻优采取逐维扰动的方法。果蝇算法不仅仅限于优化，也有很多用于解决实际问题，例如基于MFOA-SVM（Multi Fruit Fly Optimization Algorithm Support Vector Machine）算法的乳腺肿瘤识别[5]、果蝇算法对多峰值光伏最大功率跟踪仿真研究[6]、基于果蝇算法优化的BP神经网络[7]等。虽然改进算法相比传统算法而言有提高，但是还存在不足，例如SA-FOA算法虽然步长减小，精度提高，但全局搜索能力下降，容易错过最优值。因此对于FOA的研究还是有必要的。对于那些较早的遗传算法、烟花算法、蚁群算法（基于遗传算法的蛋白质复合物识别算法[8]、改进的烟花算法优化粒子滤波研究[9]、基于混合遗传-蚁群算法的（Maintenance，Repair&Overhaul，MRO）服务调度研究[10]）等而言，传统果蝇算法还不够成熟，整体寻优速度慢，收敛精度不高，容易陷入局部最佳值等。传统果蝇算法的步长是固定不变的，从而会导致陷入局部最优值和收敛速率慢等一系列问题。

本文提出了升半柯西函数，混合正切函数与柯西算子的果蝇优化算法（Tangent Cauchy Operator Fruit Fly Optimization Algorithm，TCO-FOA）根据迭代次数的变化对步长进行相应的增加或者减少。正切函数的变量采用当前迭代中最优的浓度值与最差的浓度值的和平均值与前一次迭代果蝇群中最优的浓度值与最差的浓度值的和平均值的比值。浓度平均值变化比率ARate＞1，利用升半柯西函数特点，步长在前期先均匀后呈S型增长。当浓度平均值变化比率ARate≤1，这时进入迭代后阶段，果蝇十分靠近目标源，随着浓度平均值比值减小，这时需要减少步长进行局部搜索。通过浓度平均值变化改变步长，收敛速率和寻优精度在原有的基础上都得到了有效的提高。本文将新型算法TCOFOA与传统FOA、加权果蝇算法（Weight Fruit Fly Optimization Algorithm，WFOA）、线性生成机制改进果蝇算法（Linear Generation Mechanism Fruit Fly Optimization Algorithm，LGMS-FOA）这三种算法进行了实验对比。

2 算法原理

2.1 基本果蝇优化算法

定义1果蝇有着敏感的嗅觉和视觉，它能够通过嗅觉搜寻空中各种气味，然后通过视觉找到气味的位置和同伴的位置，算法的主要过程如下：

（1）对种群规模Sizepop、迭代次数Maxgen的最大值赋值。

（2）随机化种群开始的位置，随机果蝇开始方向与距离：

（3）Dist(i)表示果蝇与初始位置的距离值，S(i)表示味道浓度判定值，S(i)为距离的倒数：

（4）判定函数中的变量为S(i)，从而得出果蝇味道的浓度Smell(i)：

（5）在所有群体里面找到浓度最佳的个体：

（6）所有的个体朝着最佳的个体飞去：

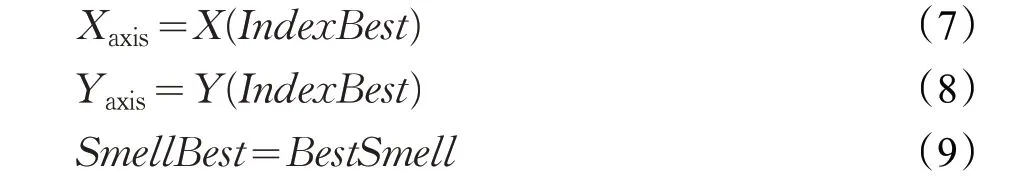
（7）迭代寻优：

将重复（2）、（3）、（4）、（5）；

判断：SmellBesti＜SmellBesti-1

如上式成立，则执行（6），如不成立则继续迭代寻优。

2.2 WFOA

WFO是根据FOA进行改进，加入了扰动因子。主要如下：

（1）C1与C2为干扰常数，C1＞C2＞0,T为当前算法所运行的迭代次数，Maximun是算法所设置的最大迭代次数。

（2）随着迭代次数的增加，步长值从C1渐渐变到C2，变化趋势不断减小，步长所能达到的最大值与最小值对应为C1与C2。

（3）WFOA的缺点是算法的表现优劣与C1和C2相关，取值不同时，产生的效果也有较大差异，而且在迭代过程中，步长的变化趋势和速率保持不变，容易错过最优解和陷入局部最优值。

2.3 LGMS-FOA

LGMS-FOA是以FOA为基础，增加了权重因子W，将原有的固定步长，更改为由权重因子影响的动态步长，W变化趋势为递减的。

果蝇所处位置：

权重参数：

其中，W0为初始权重因子，a为调节常数，gen为当前算法所处的迭代次数。该算法使用了动态调节步长，增强了局部探索能力，但是到迭代后期容易陷入局部最优值的问题没有得到有效的改善。

3 TCO-FOA

3.1 升半柯西分布

“年老”模糊集合的隶属函数为升半柯西分布，其中a=1/5,b=50,c=2。本文算法迭代前期将升半柯西分布特点运用到设置的迭代步长中，使步长在前期先均匀后呈S型增长。

升半柯西分布函数：

图1是升半柯西分布函数图像，0到a之间函数值为0，大于a时呈曲线增长，相比于指数自身的变量而言，升半柯西分布具有灵活性。小于a时均匀变化使得迭代过程不易错过最优值，大于a曲线增长扩大搜索范围，最后曲线渐渐平缓趋近于1，加快收敛速度，使得步长自适应变化。

图1 升半柯西分布

3.2 柯西分布

本文改进算法利用柯西分布的特性来设置果蝇迭代步长，使步长具有随机性，在果蝇寻优过程中能够更好地平衡全局的勘探能力和局部的寻优能力[11]。

柯西分布的分布函数：

柯西分布的密度函数：

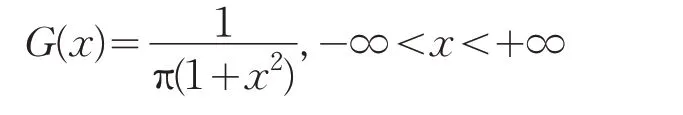
图2是柯西分布和正态分布的比较图像，相比于正态分布而言，柯西分布的整体分布更加均匀，对称轴的至高点相对于高斯分布较为平缓，而两边曲线所对应的拖尾概率较大。这样的分布特点，使柯西分布具有较大的散布特性。

图2 柯西分布和正态分布

根据柯西分布的特征，本文提出了柯西变异因子。柯西变异因子是利用柯西变异代替指数函数的变量，指数函数exp(x)与x的变化趋势相同，相对于高斯分布，柯西分布有较大的拖尾概率，整体变化平缓，根据其散布特性，柯西分布比指数原来的自变量更容易产生一个远离原点的随机数，有利于果蝇在迭代过程中脱离局部最优值。函数方程如下：

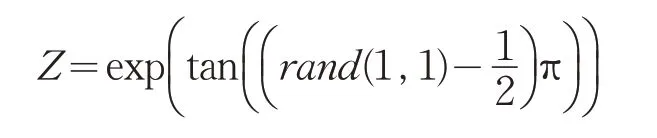
3.3 改进算法的思想

传统的果蝇优化算法中随机搜索的长度是固定不变的，随着迭代次数增加步长不会改变。迭代前期，步长过长有利于全局搜索寻优，不易陷入局部最优化。但在迭代后期，步长过长会导致局部寻优性下降，有可能错过最优值，而且算法收敛性会减慢[12]。步长过短会提高算法的收敛速度，但寻优速率会下降，而且后期极易陷入局部最优解[13]。传统算法在全局寻优和局部寻优中难以两者兼得，本文提出了一种步长根据浓度平均值变化比率改变的果蝇优化算法（TCO-FOA）。改进的算法可以很好地解决传统算法中这种不足。

前期运用升半柯西函数是为了改变传统果蝇算法中步长固定不变的问题。升半柯西函数在0到a时为0，大于a时呈S型增长，然后逐渐稳定。将升半柯西函数作为指数变量，步长先均匀增加防止错过最优值，然后呈曲线增加，后期缓慢加快收敛速度，使步长自适应化。后期运用柯西函数是因为传统果蝇算法容易陷入局部最优解。柯西函数具有较大的散布特性，有较大的拖尾概率，能更容易产生远离原点的随机数，能在迭代过程中跳出局部最优解。

本文算法通过浓度平均值变化比率对步长进行自适应动态变化。在改变步长的过程中引入了指数、升半柯西函数、正切函数和柯西算子。升半柯西函数灵活的变化使得步长变化力度自适应增长。正切函数和柯西分布本身都具有随机性，结合两种函数增大了随机性。在指数函数的情况下，使步长增加或者减少具有非均匀性和随机性。浓度平均值变化比率ARate＞1时，加快全局寻优的速率，逐步增加步长，浓度平均值变化比率ARate≤1时，为了能进行精细搜索，自适应减小步长。

3.4 TCO-FOA算法改进的步骤

将当前迭代果蝇中最优浓度值max(Smell(i))和最差浓度值min(Smell(i))的和取平均值Avg(i),与上一次迭代中最优浓度值max(Smell(i-1))和最差浓度值min(Smell(i-1))的和取平均值Avg(i-1)进行对比，得出浓度变化比率，改进如下：

本文算法把浓度平均值变化比率ARate＞1作为前期，浓度平均值变化比率ARate＜1作为后期。前期步长随机增大使全局寻优加快。后期迭代，浓度比率会随之减小，说明果蝇群体逐渐靠近目标源和自己的同伴，这时逐步减小步长，从而提高收敛速率。改进的步长如下：

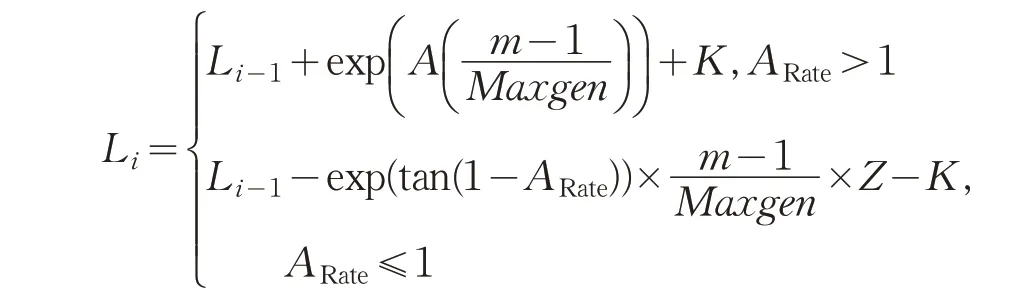
Li和Li-1分别表示当前步长和前一次迭代时的步长，ARate表示当前迭代中最优浓度和最差浓度和的平均值与前一次迭代中最优浓度和最差浓度和的平均值的比值，m表示迭代次数，Maxgen是果蝇中迭代次数的最大值，Z表示柯西算子，是利用柯西变异代替指数函数的变量。K是动态补偿因子，迭代前期加上动态补偿因子，进入迭代后期减去动态补偿因子达到平衡。通过实验K=1.5时取得最佳结果。

3.5 全局寻优和局部寻优的平衡性

（1）全局寻优

当浓度变化率大于1时，运用升半柯西函数。其中分为两部分，参数a为控制步长变化的力度。迭代次数比率小于a时，步长均匀增加防止步长变化过大错过最优值。大于a时，升半柯西函数A(x)因变量呈S型增长且不断趋近于1，步长逐渐稳定。步长增加是为了加快全局勘探速率，加快全局寻优，虽有利于全局寻优，但局部寻优性能下降，导致两者不平衡。此时设置分隔点（浓度变化率）。

（2）局部寻优

浓度变化率小于等于1时，趋近于目标值。减小步长，加快收敛速度。柯西函数较大的散布特性，能更容易产生远离原点的随机数，使不会因步长过小而陷入局部最优解[14]。算法在较小的区域进行细化搜索，保证算法的局部搜索能力[15]。从而使算法在全局寻优和局部寻优中达到平衡。

（3）算法步骤

ARate＞1：迭代次数比率小于a时，步长均匀变化。若浓度变化率不变ARate＞1，迭代次数比率大于a时，算法继续迭代，步长呈S型递增，保证全局寻优能力。直至达到ARate≤1，步长在柯西函数下递减，避免陷入局部极值。从而使算法在全局寻优和局部寻优中达到平衡。

ARate＞1：迭代次数比率小于a时，步长均匀变化。若迭代时浓度变化率改变ARate≤1，步长将停止呈S型递增，步长在柯西函数下递减，避免陷入局部极值。从而使算法在全局寻优和局部寻优中达到平衡。

3.6 大津法阈值分割

日本学者大津提出了一种确定图像二值化分割阈值的算法，其对图像的分割取得了良好的效果，原理是将图像分为前景和背景两部分。因为方差是对分布均匀性的一种度量，前景（目标）和背景的类间方差越大说明构成图像两部分的差别越大，即说明前景与背景的分割越好，所以可以认为当前所取阈值使得类间方差最大时，分割结果最好。

图像总平均灰度：

u=w0×u0+w1×u1

前景和背景图像的方差：

g=w0×w1(u0-u1)2

类间方差越大，得到的阈值最佳。传统的大津法需要对所有像素点进行灰度值计算，然后计算图像的方差，所需要的计算量较大，并且随着阈值数的增加，时间效率不断增长。本文利用改进的果蝇优化算法的快速收敛性和高精度性，对大津法阈值进行适应性求解。

4 TCO-FOA图像分割步骤

（1）将种群规模、迭代次数Maxgen的最大值赋值。令阈值t为0，即t=0。

（2）随机化果蝇开始的位置(Xaxis,Yaxis)，赋予果蝇个体随机搜索食物的方向和距离：

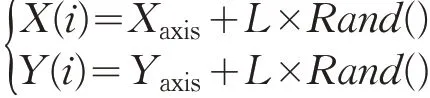
其中L为本文算法中所改进的自适应变化步长。

（3）根据式（4）计算果蝇味道浓度判定值S(i) ，浓度判定值取整，判定S(i) 是否处于[0，255]，处于此区间时继续迭代，若不在此区间内，则S(i) 浓度值为0，继续下一个循环。

（4）根据判定函数得出果蝇味道浓度，记录最佳浓度值bestsmell。

（5）令t=t+1，返回步骤（2），直到t=maxgen。

（6）根据果蝇最佳浓度值求得最优阈值。

（7）根据最优阈值对图像进行分割。

5 实验结果分析

5.1 实验设计

FOA、WFOA、LGMS-FOA、TCO-FOA四种算法采用6个适应度函数进行仿真实验[16]。表1分别为6个函数的形式和类型、搜寻的范围、达到函数目标的最优值和目标收敛的精度。算法在实验环境为Windows7下Matlab2014版本，运行内存4 GB的电脑上测试。

5.2 算法性能测试

在二维情况下，将传统FOA、WFOA、LGMS-FOA与本文算法TCO-FOA，在6个适应度函数中进行实验测试，图3表示四种算法在迭代200次寻优过程中所达到的精度值。由图可以看出，TCO-FOA算法自适应改变步长，通过运用正切函数和柯西算子在指数的情况下，收敛速率变快，易跳出局部最优值，能够达到适应度函数的目标精度值。而其他三种算法会出现收敛速度较慢或者陷入局部最优解等问题。

5.3 实验测试结果分析

5.3.1 四种算法在适应度函数下测试分析

图3 测试函数适应度变化曲线

实验采用6个适应度函数，在已知适应度函数的目标精度之下对FOA、WFOA、LGMS-FOA、TCO-FOA进行了20次独立测试，测试结果如表2所示。表中的平均值表示进行20次独立测试时算法在适应度函数中能够达到的精度值和的平均值[17]。在测试中方差表示算法的稳定性效果。从表2可以看出，FOA、WFOA、LGMSFOA在测试函数下多数没有达到已知的精度值，而且极易陷入局部最优解。TCO-FOA对比与另外三种算法而言达到了测试函数的目标精度值，而且测试过程中的稳定性高于另外三种算法。实验结果证明了混合动态改变步长的果蝇优化算法的高效性。

表3是四种算法在6个适应度函数中，分别将维度设置为2和30情况下，达到适应度函数的目标精度的平均迭代次数和成功率的比较。将算法中迭代次数赋值为2 000，独立运行20次。从表中可以看到，无论在2维还是在30维中，本文算法都达到了目标精度值而且成功率是100%，算法在运行中所迭代的平均次数也比其他算法少。其他三种算法在2维和30维中都难以达到目标精度，而且稳定性比较差，在迭代后期极易陷入局部最优解。本文算法稳定性强，达到目标精度的平均迭代次数小，不仅收敛速度优于其他三种算法，而且能跳出局部最优值。综上所述，TCO-FOA无论是在低维还是在高维情况下，都能保持寻优的稳定性和比较高的成功率。

表1 测试函数

5.3.2 改进算法收敛性分析

从表2可以看出，本文算法在6个测试函数中都达到了目标精度值，其他三种算法在测试函数中达到目标精度的较少。表明在收敛精度上本文改进的算法优于其他三种果蝇算法。而且从方差可以看出，本文算法在实验中稳定性高于其他三种算法。从表3的迭代次数可以看出，传统果蝇算法平均迭代次数比较大，另外两种改进算法相对于传统算法而言迭代次数相对减少，增加了收敛速度。但本文改进的算法不仅迭代次数相对于其他三种算法少，收敛速度快，而且在6个适应度函数中，迭代成功率达到了100%。从两个表中可以看出，本文算法无论在收敛精度还是在收敛速度上都优于另外三种算法。

5.3.3 大津法阈值分割实验分析

分别用传统果蝇算法、TCO-FOA、LGMS-FOA、WFOA对大津法进行阈值优化，各进行30次，并统计优化大津法的平均阈值适应度函数值和方差，如表4所示。从优化结果来看，TCO-FOA都取得了最大的最佳阈值适应值，这说明TCO-FOA在优化大津法阈值方面能取得比其他算法更好的效果。从方差来看，TCO-FOA比其他算法表现得都较稳定，这得利于TCO-FOA柯西分布容易产生远离原点的随机数作为指数的算子进行扰动，兼顾了全局和局部，从而提高了种群的多样性。

从图4可以看出传统果蝇算法图像分割模糊，且分割效果不明显。LGMS-FOA、WFOA算法在图像中能分割出大致轮廓，但是在细小部分的分割效果不佳，且存在噪点。本文改进的算法无论在去噪能力还是在分割效果上都优于其他三种算法。

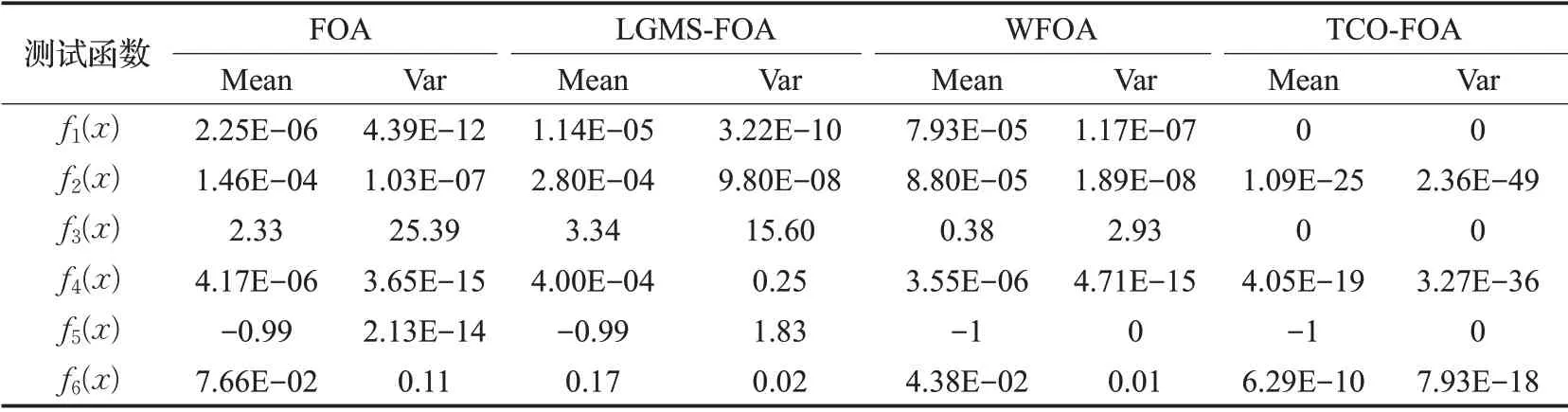
表2 四种算法测试结果

表3 目标精度下的平均迭代次数与成功率对比

表4 各算法取最佳阈值的适应值平均值和方差

图4 测试图像分割结果

6 结束语

传统果蝇算法难以跳出局部最优值，收敛速度慢，精度不高。本文改进的算法在步长中运用正切函数和柯西算子扩大了随机性，使全局搜索能力得到优化。运用指数，使步长变化具有随机性和非均匀性，迭代前期利用升半柯西函数特点自适应增大步长，加快收敛速度，后期随机性减小步长，提高精度。相比于其他三种算法而言，本文算法在精度值和收敛速度上都较高。将改进的果蝇算法应用到大津法阈值的优化上，通过与其他算法进行仿真实验对比，本文算法在阈值优化的效果和稳定性上都要优于其他算法。随着阈值数的增大，算法的稳定性有所降低，这也是其他算法存在的问题，如何更好地提高算法的稳定性，是未来研究的重点。