一类生物系统的参数辨识方法及其应用

徐恭贤，邱 添，贾府生，魏顺行

1.渤海大学 数理学院，辽宁 锦州121013

2.渤海大学 数字出版大数据挖掘与治理及呈现技术标准实验室，辽宁 锦州121013

1 引言

随着生物工程技术的迅速发展，越来越多的学者对S-型生物系统的参数辨识问题进行了深入研究[1-9]。例如，Chen等[1]基于混合变量多目标进化算法推断了S-型生物系统的模型参数；Sarode等[2]利用遗传算法对S-型生物系统进行了反问题研究；Kimura等[3]应用分解法把一个原问题分解成若干个子问题，进而对每一个子问题进行了参数辨识分析；Tsai等[4]将微分方程转化为代数方程后应用混合差分算法求解参数辨识的优化模型；于超[5]通过五点中心差分算法推断了S-型生物系统的模型参数；刘丰[6]、徐恭贤等[7]应用三次样条插值方法研究了S-型生物系统的参数辨识问题。

本文针对S-型生物系统的参数辨识问题，基于修正配置和B样条插值，提出了一种有效的参数辨识方法。应用研究表明，本文方法能够获得较好的参数辨识结果。

2 生物系统的数学描述

考虑如下S-型生物系统：

其中，x=(x1,x2,…,xn)T∈Rn+为生物系统的代谢物浓度向量，t∈[0,T],f=(f1,f2,…,fn)T∈Rn。

式（2）中，αi、βi为速率常数；gij、hij为动力阶；向量p=(αT,βT,GT,HT)T,pL≤p≤pU,p中的α、β、G、H可分别表示为：

3 参数辨识问题

设xei(tk)表示第i个代谢物浓度在时刻t=tk时的实验值；xeimax表示第i个代谢物浓度实验值的最大值；Ns表示时刻点的个数；xi(tk)表示第i个代谢物浓度在时刻t=tk时的模型计算值；ẋei(tk)表示第i个代谢物浓度在时刻t=tk时实验值的速率；ẋi(tk)表示第i个代谢物浓度在时刻t=tk时模型计算值的速率；ẋeimax表示第i个代谢物浓度速率的最大测量值。

为了得到生物系统（1）的速率常数和动力阶，本文以极小化误差函数为优化目标，建立了如下参数辨识模型：

参数辨识问题（9）具有如下性质：

性质1参数辨识问题（9）存在最优解p∗∈U。

证明 设U={p|pL≤p≤pU,p∈，显然U⊂是紧集。又因为x0∈Rn+,p∈U且fi∈C1(Rn+×U)，故由常微分方程的解存在唯一性定理可知，对∀p∈U，生物系统（1）存在唯一解，且该解关于p∈U是连续的，所以J关于x是连续泛函，故参数辨识问题（9）存在最优解p∗∈U。

4 参数辨识问题的求解方法

为了求得参数辨识问题（9）的最优解，利用修正配置法将微分方程近似表示为如下代数方程：

其中，ηk=tk-tk-1。则参数辨识问题（9）可以转化为如下非线性规划问题：

为了求解非线性规划问题（11），本文应用B样条插值方法估计实验值的速率B样条插值是一类常见的样条函数[10]，一般选择阶次为4或5的B样条能够得到较好的插值效果。关于B样条插值的基本原理及其求解过程可以参见文献[10]。B样条插值方法的应用可以在Matlab中完成，采用Matlab样条插值工具箱[11]的spapi命令即可计算实验值的速率

非线性规划问题（11）的求解也可以在Matlab中实现，应用Matlab优化工具箱[11]的fmincon命令即可求得最优解。

综合前文所述，本文的参数辨识方法可描述如下：

步骤1构建生物系统（1）的参数辨识优化模型（9）。

步骤2应用B样条插值（比如Matlab样条插值工具箱的spapi命令）估计实验值的速率

步骤3应用修正配置公式（10）将生物系统的微分方程（1）近似表示为代数方程，从而将动态优化问题（9）化为非线性规划问题（11）。

步骤4通过步骤4.1至步骤4.4辨识出生物系统（1）的模型参数。

步骤4.1取初始参数值p(0)∈U，ε＞0。令迭代次数r=0。

步骤4.2在算法的第r(r≥1)次迭代，应用非线性优化方法的序列二次规划算法求解非线性规划问题（11）。设动力阶参数gij和hij的最优值分别为和。

步骤5输出模型参数的辨识值p∗。结束参数辨识过程。

5 仿真研究

例1考虑如下生物系统：

生物系统（12）、（13）中各参数的真实值为：α1=3；α2=1；β1=1；β2=1；g11=0；g12=-2；g21=0.5；g22=1；h11=0.5；h12=1；h21=0；h22=0.5。本例中，取x(0)=(0.2,0.5)T，T=8，ηk=0.1。

由式（9）可得如下参数辨识优化模型：

表1给出了无噪声条件下本文方法的参数辨识结果，相应的最优目标函数值为7.446 2×10-8。从表1可以看出，本文方法得到的辨识结果接近参数的真实值。

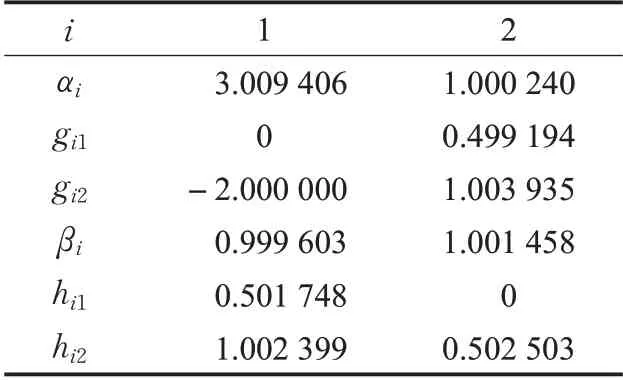
表1 无噪声条件下例1的辨识结果

表2给出了本文方法与已有方法[5-6]的结果比较。误差函数e表示参数辨识值与真实值之差的绝对值之和，即：

表2 例1中误差e的比较

通过表2可以看出，本文方法获得了较低的误差e值，分别比文献[5-6]方法降低了32.86%和0.21%，说明本文方法更为精确。

将表1的参数辨识结果代入生物系统（12）、（13）中，得到如图1所示的代谢物浓度随时间变化曲线。从图1可以看出，各代谢物浓度的计算值与实验值基本一致。

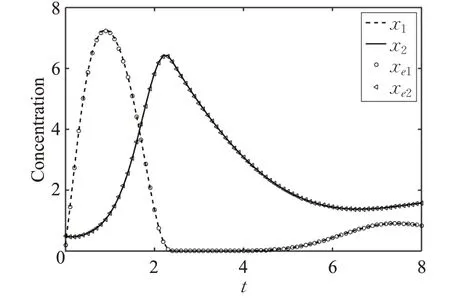
图1 无噪声条件下例1的仿真结果

为考察本文方法在有噪声条件下的性能，在代谢物浓度的实验值xei(tk)中加入5%的高斯白噪声，参数辨识后生物系统的仿真结果如图2所示。从图2中可以看出，在噪声情况下，本文方法仍能得到较好的参数辨识结果。

图2 噪声条件下例1的仿真结果

例2考虑如下生物系统：

生物系统（16）～（19）中各参数的真实值为：α1=12；α2=8；α3=3；α4=2；β1=10；β2=3；β3=5；β4=6；g11=0；g12=0；g13=-0.8；g14=0；g21=0.5；g22=0；g23=0；g24=0；g31=0；g32=0.75；g33=0；g34=0；g41=0.5；g42=0；g43=0；g44=0；h11=0.5；h12=0；h13=0；h14=0；h21=0；h22=0.75；h23=0；h24=0；h31=0；h32=0；h33=0.5；h34=0.2；h41=0；h42=0；h43=0；h44=0.8。本例中，取x(0)=(10,1,2,3)T，T=5，ηk=0.1。

由式（9）可得如下参数辨识优化模型：

表3给出了无噪声条件下本文方法的参数辨识结果，相应的最优目标函数值为3.795 466×10-8。从表3可以看出，本文方法的辨识结果接近参数的真实值。

表3 无噪声条件下例2的辨识结果

表4给出了本文方法与已有方法[5-6]的结果比较。误差函数e表示参数辨识值与真实值之差的绝对值之和，即：

表4 例2中误差e的比较

通过表4可以看出，本文方法获得了与文献[6]方法相同的误差e值，但比文献[5]方法降低了1.93%。

将表3的参数辨识结果代入生物系统（16）～（19）中，得到如图3所示的代谢物浓度随时间变化曲线。从图3可以看出，各代谢物浓度的计算值与实验值基本一致。

图3 无噪声条件下例2的仿真结果

为考察本文方法在有噪声条件下的性能，在代谢物浓度的实验值xei(tk)中加入5%的高斯白噪声，参数辨识后生物系统的仿真结果如图4所示。从图4中可以看出，在噪声情况下，本文方法仍能得到较好的参数辨识结果。

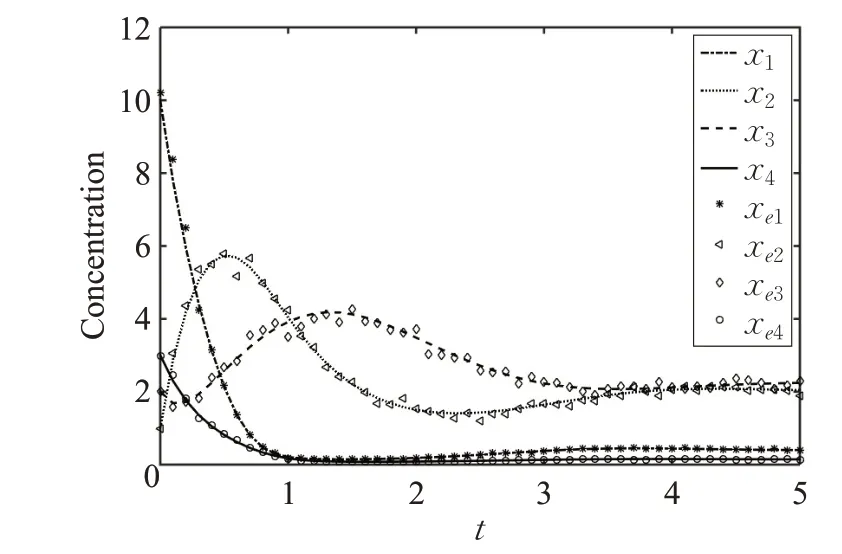
图4 噪声条件下例2的仿真结果

6 应用于甘油生物发酵系统

基于本文方法，研究甘油生物发酵生产1，3-丙二醇系统[12-16]的参数辨识问题。

甘油生物发酵生产1，3-丙二醇的S-型生物系统可表示为：

其中，x1表示生物量的浓度(g⋅L-1)，x2表示甘油的浓度(mmol⋅L-1)，x3表示1，3-丙二醇的浓度(mmol⋅L-1)，x4表示乙酸的浓度(mmol⋅L-1)，x5表示乙醇的浓度(mmol⋅L-1)。式（22）～（26）的参数辨识优化问题为：

图5 生物量变化曲线

图6 甘油浓度变化曲线

图7 主要产物1，3-丙二醇浓度变化曲线

本例中，取x0=(0.1905,400.043,0,0,0)T,T=6。图5～图7分别表示甘油生物发酵过程中生物量、甘油、主要产物1，3-丙二醇浓度随时间的变化曲线，其中离散点表示实验的观测数据。由拟合曲线可以看出，应用本文方法得到的S-系统能较好地描述甘油生物发酵系统。

7 结束语

针对S-型生物系统的参数辨识问题，本文给出了以极小化误差函数为优化目标的参数辨识优化模型，并为其设计了有效的求解方法。与已有方法相比，本文方法能够获得更为准确的参数辨识结果。另外，将本文方法应用于甘油生物发酵系统的参数辨识问题中，取得了较好的应用效果。