麦克风阵列下互相关函数分类的声源定位

张岁岁，黄丽霞，王 杰，张雪英

太原理工大学 信息与计算机学院，太原030024

1 引言

声源定位技术是一种利用麦克风阵列接收并处理声场信号以确定声源位置的技术，其在基于麦克风阵列的应用中发挥着越来越重要的作用，如视频会议[1]、语音增强、智能家居设计[2]、语音识别、智能机器人[3]、智能视频监控系统[4]等。

目前在基于麦克风阵列的声源定位算法方面已经有了比较成熟的理论和方法。传统的声源定位算法大致可以分为两大类[5]：单步法和双步法。最大似然算法（Maximum Likelihood，ML）是单步法中最主要的算法，此类算法中最熟悉的即可控相应功率相位变换（Steered Response Power-Phase Transformation，SRP-PHAT）算法；另一种单步算法即高分辨率谱估计算法。双步法中，第一种涉及到了到达时间差（Time Difference of Arrival，TDOA）估计；另一种是基于自适应特征值分解的子空间法和广义特征值分解。双步法中的基于时延估计的算法因其计算量小，便于实时处理，在实际的定位系统中应用较多。然而室内实际环境中存在各种干扰和影响等，会对系统的定位存在很强的混响作用。传统的声源定位方法在高混响的恶劣环境下，定位精度下降。

近年来，机器学习和模式识别技术已经被用来解决声源定位问题。Strobel等人[6]提出一种基于时延估计分类的声源定位算法，详细研究了ML分类和基于直方图的分类方法，在恶劣的声学条件下，与传统算法和ML分类算法相比较，基于直方图分类的方法定位准确率提高60%以上。Zhang等人[7]提出了一种基于双麦克风的多声源定位技术，该技术利用语音特性和聚类及线性拟合技术。Sun等人[8]在混响环境中利用圆形麦克风阵列进行声源数目估计和定位，通过在选定的TF（Time-Frequency）点上进行单声源定位来解决这一问题，用无限个高斯混合模型得到到达方向（Direction of Arrival，DOA）估计，采用贝叶斯方法估计声源和DOA的数目。该算法最大的优势是对声源的个数没有限制。Lee等人[9]提出了一种新的k均值聚类算法，即竞争k均值聚类算法。将其性能与自适应k-means++算法进行了比较，验证了算法的有效性。最后将其应用于多声源定位中，取得了满意的效果。Salvati等人[10]提出了一种在混响环境中使用加权最小方差无失真响应（Weighted Minimum Variance Distortionless Response，WMVDR）的近场声源定位算法。基于机器学习计算WMVDR的可控响应功率，采用支持向量机（Support Vector Machine，SVM）分类器对融合分量进行选择。Sun等人[11]提出了一种新的加权决策方法（Weighted Decision Making Method，WDMM），通过重新访问相邻子空间的概率，有效地提高了基于似然分类算法的定位精度。

本文主要研究了基于相位变换加权函数分类的声源定位问题，引入了Fisher加权朴素贝叶斯分类器。通过PHAT互相关函数得到特征向量，然后利用Fisher加权朴素贝叶斯分类器估计声源位置。设计并实现了仅基于两个麦克风的声源定位系统，并将改进的定位算法在实际环境中进行了声源定位实验。

2 加权广义互相关函数特征提取

2.1 信号模型

在实际环境中，室内麦克风阵列接收到的信号不仅包括声源发出的信号，而且还包含房间背景噪声和房间混响。对于由M个阵元组成的麦克风阵列，第m个麦克风接收到的信号可由下式表示：

其中，s(n)表示声源；hm(n)表示声源到第m个麦克风的房间脉冲响应，包含多径传播和衰减信息；wm(n)表示房间背景噪声；∗表示卷积算子。本文重点研究混响对定位算法的影响，即假设wm(n)=0。

其中，Prl(Y' )由均值向量Url和协方差矩阵Qrl决定。

2.2 加权广义互相关函数

两个麦克风接收到的信号可以分别表示为x1(t)、x2(t)，两个信号的广义互相关函数（Generalized Cross-Correlation，GCC）等于两信号互功率谱的傅里叶变换，如下式表示：

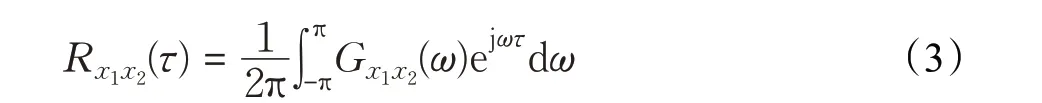
其中，Gx1x2(τ)=x1(ω)x∗2(ω)表示被测信号x1(t)、x2(t)的互功率谱密度函数；x1(ω)、x2(ω)分别表示麦克风m1m2接收到信号x1(t)、x2(t)的傅里叶变换；∗表示复共轭。

但在高混响环境下，容易引起互相关函数峰值变宽，出现假峰值。为了锐化峰值，在信号中加入不同的加权函数，首先抑制混响干扰，提高互相关函数的抗混响能力。因此，式（3）可以描述为：

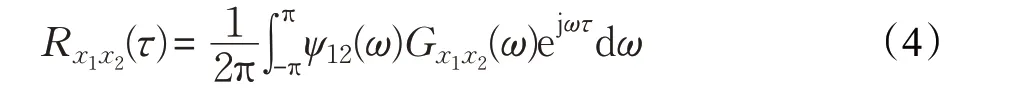
这里，ψ12(ω)表示不同的加权函数，实际应用中，选择最合适的加权函数对GCC函数的性能非常重要[13]。很多文献中提出了各种加权函数，本文主要涉及PHAT加权函数：

将式（5）带入式（4），两信号的广义互相关函数如下：

2.3 特征提取

基于互相关函数分类的声源定位算法分为两个阶段：训练阶段和定位阶段。

算法训练阶段如图1所示。朴素贝叶斯分类器的训练阶段就是利用特征向量进行训练，得到相应特征的均值uij和方差σ2ij，由广义互相关函数Rx1x2(τ)形成特征向量。

图1 算法训练阶段

训练阶段位置rl,l=1,2,…,L处的特征向量为：

这里，D表示两个麦克风之间的距离；c表示声速；fs表示采样频率；δ表示因子，在后面的实验中设为1.67；round(⋅)表示取整。

3 基于互相关函数分类的声源定位

3.1 朴素贝叶斯理论

朴素贝叶斯分类器[14]在估计类条件概率密度时假设属性之间条件独立，即特征独立性假设，高斯分布通常被用来表示连续属性的类条件概率分布。高斯分布的两个参数分别是均值uij和方差，对于每个类yj，属性Xi的类条件概率由下式表示：

参数uij可以用类yj的所有训练记录关于Xi的样本均值来估计。同理，可以用这些训练记录的样本方差来估计。

3.2 基于Fisher加权的朴素贝叶斯分类器

NBC模型认为[15]，所有特征对于最终的分类结果具有同等重要的意义（即权重为1）。但是单个特征和类别之间存在不同程度的相关性，朴素贝叶斯算法直接忽略了这种相关性，可能会增加分类的误判。本文将特征加权算法与朴素贝叶斯分类器相结合，根据其对分类的重要性给出不同的权重。属性权重越大，属性对分类的影响越大。将NBC扩展到加权NBC（Weighted Naive Bayes Classifier，WNBC），以提高分类器的性能。本文采用Fisher判别准则函数，确定各个特征的分类权重。

在位置rl,l=1,2,…,L处分别使用M帧数据估计单个特征的均值、方差和权重，即：

类间离差值和类内离差值分别为：

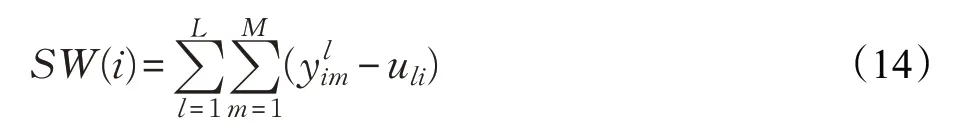
则特征yi,i=1,2,…,2τm+1的Fisher准则判别函数如下：

在Fisher判别理论中，类间离差值被用来描述不同类之间的差距。类内离差值用来描述同一类样本之间的差距。

当特征的权重高于平均值时，权重应大于1，以增加其对分类的影响；当特征的权重低于平均值时，权重应小于1，以减少其对分类的影响。

最终确定权重的方法定义如下：

3.3 基于互相关函数分类的声源定位

基于互相关函数分类的声源定位算法的测试阶段如图2所示。

图2 算法测试阶段

由以上内容可知，假设对于每个特征yli,i=1,2,…,2τm+1是相互独立的，那么测试阶段位置rl,l=1,2,…,K的特征向量Y(rl)的概率密度函数由下式给出：

因此，采用Fisher加权的朴素贝叶斯分类器的判别函数为：

假设在测试阶段使用多帧特征向量即特征向量集合Y'(rl)={Yt(rl), t=1,2,…,N}，则集合Y'的概率密度函数为：这里表示第l个位置第t帧测试数据的第i个特征。

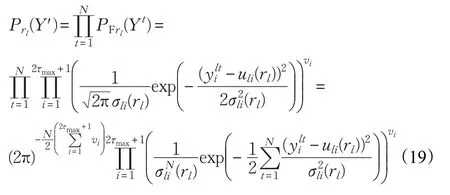
最终声源位于使得概率密度函数Prl(Y' )或者Prl(Y)取得最大值的位置，即：

4 实验结果与分析

4.1 仿真实验

4.1.1 实验环境和条件

实验用镜像法（Image）生成房间脉冲响应，来模拟一个普通的实验室环境，房间尺寸为6 m×4 m×3 m，两麦克风的坐标分别是M1（3.85，2.5，1.2）、M2（4.15，2.5，1.2），采样率16 kHz，声源距离两个麦克风中点的距离距离为2 m。假设房间墙壁的反射系数β相同，根据混响时间T60与反射系数β的关系可得，反射系数越大，混响时间越大。训练和定位阶段使用双门限端点检测算法对信号进行端点检测，并对信号进行分帧，帧长512，帧移256，每帧信号加矩形窗。在实验过程中，声源的位置有17个，即声源与两麦克风中点的夹角分别为(10°,20°,… ,170°)。仿真房间平面图如图3所示。

4.1.2 仿真结果与分析

为了便于描述，将使用朴素贝叶斯分类器的分类算法标记为NBC_P，将使用基于Fisher加权的朴素贝叶斯分类器的分类算法标记为FWNBC_P。

（1）房间混响的影响

在本实验中，主要验证了算法在不同混响环境下的定位性能。测试帧数分别为4帧、5帧和6帧。

图3 仿真房间平面图

图4实验结果表明，在不同的混响β=0.2,0.4,0.6,0.8环境下，与NBC_P算法相比，FWNBC_P算法在不同测试数据帧下定位精度都有一定程度的提高。当使用较少的测试数据帧（4帧）时，两种算法的精度随着混响的增加而显著降低，与NBC_P算法相比，FWNBC_P算法的定位准确率平均提高11.71%；当使用较多的测试数据帧（5帧）时，与NBC_P算法相比，FWNBC_P算法的定位准确率平均提高7.73%。当使用更多的测试帧（6帧）时，FWNBC_P算法表现出更好的性能，定位准确率平均提高16.16%。

通过以上分析，可以看出在不同混响条件下，与NBC_P算法相比较，FWNBC_P算法的定位精度都有一定程度的提高。

（2）测试数据帧的影响

在本实验中，主要验证了算法在不同测试数据帧数下的定位性能，反射系数分别为0.4、0.6、0.8。

图4 不同混响环境下不同帧测试数据的两种算法的定位精度

图5 不同测试数据帧时两种算法的定位准确率

图5实验结果表明，在不同的测试数据帧下，与NBC_P算法相比，FWNBC_P算法在不同测试数据帧下定位精度都有一定程度的提高。当混响较低(β=0.4)时，两种算法的准确率随着测试数据帧数的增加而显著提高，与NBC_P算法相比，FWNBC_P算法的定位准确率平均提高10.54%；当混响增强(β=0.6)时，与NBC_P算法相比，FWNBC_P算法的定位准确率平均提高11.32%；当处于强混响环境(β=0.8)时，FWNBC_P算法的定位准确率平均提高4.88%。

通过以上分析，可以看出在不同混响条件下，随着测试数据帧数的增加，两种算法的定位准确率都有所提高。与NBC_P算法相比较，FWNBC_P算法有更好的鲁棒性。

4.2 真实实验

4.2.1 实验环境

为了评估基于互相关函数分类的定位算法在真实环境中的可行性，在一个小型会议室中进行了初步的真实数据的实验，房间大小是8 m×7 m×3 m。实验过程中存在一定的噪声和混响，噪声包含电脑运转的声音以及房间外人员走动的脚步声，房间内有桌椅、书橱以及墙壁等障碍物，实验过程中尽量保证声源与麦克风之间不存在障碍物。使用两元麦克风阵列，两麦克风的间距为25 cm，采样频率为8 kHz。搭建的实际环境下的定位图如图6所示。整个系统分为软件和硬件两部分，如图7所示。

图6 实际环境下的声源定位系统

图7 声源定位系统的组成

4.2.2 系统组成

（1）麦克风阵列。阵列采用两元线阵麦克风阵列，麦克风使用了MP40传声器。MP40传声器是1/4英寸预极化自由场测量传声器，无需极化电压，是一款与前置放大器不可分离的产品，具有灵敏度高、稳定性好、可靠性高等特点。

（2）采集卡。本文采用SKC公司的USB数据采集卡Q801，这是一款基于USB总线的高性能多功能数据采集卡，具有8路单端16位高速同步模拟信号采集功能。

4.2.3 工作过程

本声源定位系统的实现过程如下：首先将麦克风按照一定的结构组成麦克风阵列（一字线阵），进行系统的初始化；然后对各个麦克风进行AD采样；如果麦克风阵列接收到音频信号，则将采样后的音频信号数据传给PC机；利用PC机对音频信号进行相关去噪和预处理，最后利用本文算法进行互相关函数的鉴别，从而确定最终声源位置。

4.3 实验结果分析

本实验采用不同的声源位置，声源距离两麦克风中点的距离分别为1.0 m、1.5 m、2.0 m，测试数据帧分别使用5帧、6帧，麦克风坐标M1(-0.125,0,0),M2（0.125，0，0），真实实验过程中设计了18组实验来估计声源位置。表1给出了使用5帧测试数据且声源距离麦克风阵列中心距离分别为1.0 m、1.5 m、2.0 m时的不同测试位置的定位准确率。

表1 真实实验不同测试位置定位准确率%

与仿真实验相比，真实实验过程中存在更多的影响实验精度的因素，包括桌椅、书橱、实验人员、四周墙壁等障碍物以及房间外的不同噪声、采集卡和麦克风阵列的精度等，造成真实实验结果与仿真实验相比较，定位精度有一定程度的降低。

图8实验结果显示，FWNBC_P算法在实际环境下搭建的定位系统中定位准确率优于NBC_P算法。声源距离为1.0 m时，FWNBC_P算法的定位准确率与NBC_P算法相比，平均提高1.62%；声源距离1.5 m时，FWNBC_P算法的准确率与NBC_P算法相比，平均提高0.46%；声源距离为2.0 m时，与NBC_P算法相比，FWNBC_P算法的准确率平均提高3.24%。

5 结束语

图8 实际环境下系统的定位准确率

本文主要研究了基于相位变换加权的互相关函数分类的声源定位问题，引入了Fisher加权朴素贝叶斯分类器。通过PHAT互相关函数得到特征向量，然后利用Fisher加权朴素贝叶斯分类器估计声源位置。同时，设计并实现了仅基于两个麦克风的声源定位系统，并将改进的定位算法在实际环境中进行了声源定位实验。实验结果显示，与参考算法NBC_P相比较，改进算法在仿真实验和真实实验中，都有较好的鲁棒性。在今后的研究工作中，应当考虑噪声对算法准确率的影响，以及考虑将该算法应用于多声源定位研究中。