基于k-近邻与局部相似度的稀疏子空间聚类

郑 毅，马盈仓，杨小飞，续秋霞

西安工程大学 理学院，西安710600

1 引言

随着信息时代的蓬勃发展，对数据进行合理有效的分析和处理成为当代科学研究领域越来越重要的课题。但现今的数据数量大、维度高，而且结构也越来越复杂，使得相关研究面临着很大的困难[1]。为此，人们提出了很多方法来解决这些问题，其中子空间聚类方法凭着其想法自然和假设合理的优势，受到人们的关注，并得到了深入的研究[2]。在过去几年中，子空间聚类方法在机器学习[3]、图像处理[4]、计算机视觉[5]以及系统辨识[6]等众多领域都有着广泛的应用，并针对这些高维数据集取得了较为理想的结果[7]。

子空间聚类假设高维数据分布于多个低维子空间的并上，例如图1[8]所示，其中的三维数据本质上是由一个二维平面和两条一维直线所组成。因此，在这一假设前提下，人们希望寻找出合理的子空间分割方案，以此来将数据分划成不同的簇。经过多年的发展和研究，人们已经提出了很多子空间聚类方法，总体来说大致分为五类，分别是基于矩阵分解[9]、基于代数[10-11]、基于迭代[12-13]、基于统计[14-15]以及基于谱聚类[16-17]。

图1 子空间聚类数据示意图

稀疏子空间聚类是基于谱聚类的一种子空间聚类方法，作为近些年来的一个研究热点[18]，其主要思想是将每一个数据都表示为除自己以外的其他数据的线性组合，以此来挖掘数据在空间分布中的结构信息。因此，核心问题在于求解出恰当的仿射矩阵，并以此构造出相似度矩阵用于谱聚类[19]，得到最终的聚类结果。为了得到更加“恰当”的仿射矩阵，获得更好的聚类结果，通常在算法模型中对仿射矩阵A加上各种形式的限制和约束，迫使A具有理想结构，这种理想结构能够帮助发现和挖掘数据背后的潜在信息，以利于聚类。

稀疏子空间聚类模型（Sparse Subspace Clustering，SSC）[20]对仿射矩阵A施加l1范数，使得仿射矩阵A具有稀疏性，这样可从全局角度自动选择近邻点，消除冗杂数据间的相关性。低秩表达模型（Low Rank Representation，LRR）[21]对仿射矩阵A施加核范数，使得仿射矩阵A具有低秩性，能够更好地捕获数据的全局结构，尤其当存在损坏的数据时可以进行稳健的子空间分割。最小二乘子空间聚类模型（Least Squares Regression，LSR）[22]对仿射矩阵A施加F范数，可以保持数据的聚集性。基于二部图的快速聚类模型（Fast Clustering Based on Bipartite Graph，FCBG）[23]通过对A的拉普拉斯矩阵LA施加秩约束，可以保持其类簇结构。基于TL1范数约束的子空间聚类模型（Subspace Clustering Method Based on TL1Norm Constraints）[24]对仿射矩阵A施加TL1范数，使A具有稀疏性并具有块对角结构，并在含噪的情况下具有优越的鲁棒性。二次规划子空间分割模型（Subspace Segmentation via Quadratic Programming，SSQP）[25]要求矩阵ATA稀疏且A正定，以获得更理想的聚类结果。隐低秩表示（Latent Low Rank Representation，LatLRR）模型[26]，对列表示系数矩阵和行表示系数矩阵同时施加低秩约束，用行数据信息弥补列数据信息的污染或缺损，极大地提高了聚类性能。这些年来，人们又陆续提出了很多范数（如范数[27]，范数[28]等）来约束仿射矩阵，都是为了使仿射矩阵具有更加理想的结构，以利于聚类。

然而，目前提出的大多数稀疏子空间聚类方法都存在两个共同的弊端。第一，在模型中对仿射矩阵A直接施加的各种约束本质上是面向全局的，这样没有充分利用数据在局部的有效信息，在对整体进行优化的过程中忽略了对数据局部结构的挖掘。第二，由于谱聚类是基于图论的，使用时要求相似矩阵是对称正定的，因此在求解出仿射矩阵A后，人们一般考虑直接用得到相似矩阵，但从最初和实质看来，仿射矩阵的含义在于数据进行线性表示时能够更好地贴合原数据，虽然在某种程度上间接反映了数据间的相似关系，但两者在本质上不完全等同。

为了克服上述两个问题，本文提出一种基于k-近邻与局部相似度约束的稀疏子空间聚类算法（Sparse Subspace Clustering Based on k-Nearest Neighbors and Local Similarity，k-LSSSC，k-LS3C）。首先，引入k-近邻，可以有效利用数据点的局部信息，挖掘出数据的局部结构。其次，从图论中相似矩阵的构造获得启发，利用数据点间的距离来辅助构造仿射矩阵A。具体来说，当xj与xi距离较小时，Aij的值应较大，这样最终得到的相似矩阵中对应的值也相对较大。反之，当xj与xi距离较大时，Aij的值应较小，这样最终得到的相似矩阵中对应的值也相对较小。

值得说明的是，引入k-近邻后不仅可以发挥数据在局部的作用，还可以剔除大量的不相关点，使得计算更为简便。而且，由于考虑了k-近邻，仿射矩阵只在部分元素上存在用于线性表示的非零值，这也进一步加强了仿射矩阵的稀疏性。此外，k的选取比较灵活，当数据的线性相关性很强时，选择适当少的k值就能达到很好的效果。当数据的噪声较多时，选择适当大的k值还能够使得算法更加鲁棒，不易被“错误”的数据所影响[29]。

2 相关工作

2.1 稀疏子空间基础模型

对一组由n个d维数据点组成的数据集X=(x1,x2,…,xn)∈Rd×n，假设它本质上属于c个线性子空间的并。在理想的情况下，子空间聚类将数据分割成不同的类别，每一个类别对应其中的一个子空间，属于同一子空间内的数据点互相之间有着较强的线性关系。

为了避免平凡解，即数据点不用自身进行自我表示，常常令Aii=0。同时为了使得仿射矩阵具有稀疏性，对A施加l1范数，这样就得到了目前子空间聚类领域最基础的模型之一，如式（2）所示：

2.2 仿射矩阵基本约束

由于仿射矩阵最后需要转化为相似矩阵，一般约定数据在进行线性表示时选取的系数为正值，因此约束∀i,j,Ai,j≥0。同时由于数据被分割到每一个低维的子空间后，彼此之间非常容易出现很强的线性关系，为了简化计算，约定A的列和为1，即每个数据点由其他数据线性表示的系数之和为1。把系数值进行归一化约束到[0，1]区间后，可以有效处理一些特殊的情形。如图2所示，在某一平面内，x1可以用x2,x3,x4进行线性表示，如果不加任何限制，表示系数可以有很多种不同的组合选择，例如可以表示为x1=0.25x2+0.25x3+0.50x4,也可为x1=5x2+5x3+10x4。此时，若加上列和为1的限制，能够增强模型的稳定性，同时把数据约束在比较均衡的范围内，方便计算。

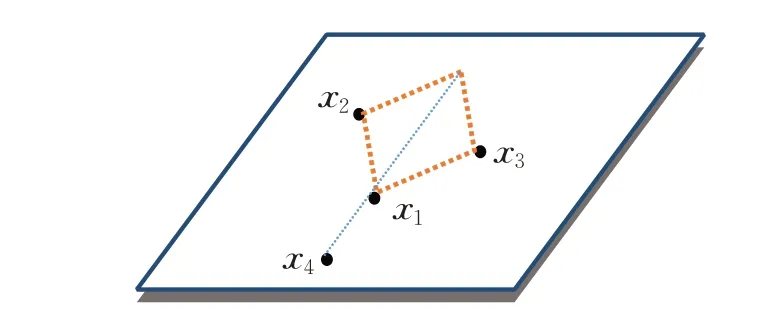
图2 线性表示图示

2.3 稀疏子空间模型引入k-近邻的合理性

前面提到，仿射矩阵的构造应该同时考虑数据的“整体”和“局部”，尤其当数据分割到低维的子空间后，局部信息有着不可忽略的作用。数据在局部的一个重要信息就是k-近邻，本节为了说明数据局部信息的重要性，同时也为了说明在稀疏子空间聚类研究中引入k-近邻的合理性，设计如下实验。

由于稀疏子空间聚类是基于谱聚类的，在一般的谱聚类中，用数据点之间的距离信息就可以构造相似矩阵。本节分别面向数据全局构造全连接矩阵，以及面向数据局部构造k-近邻矩阵，构造时采用最常用的数据间欧式距离。此外，k-means同样是基于数据点的距离信息，将距离当作数据点与簇中心的相似度进行聚类。上述三种聚类方法运用到一些二维数据集，结果如图3～图5所示。

图3是典型的基于中心的簇，属于凸状数据集。对于这种凸状数据集，上述三种方法都能准确聚类。但图4所示的双月数据集以及图5所示的螺旋数据集均属于非凸数据集，对于这种非凸数据集，k-means依然将数据聚成凸形簇，不能取得理想的结果。同样的，由于在全连接矩阵聚类中，数据点和其余所有点都有权值相连，这意味着簇间的连接复杂，影响了最后的聚类性能。而在k-近邻矩阵聚类中，一般近邻的数据都属于同一簇，最后得到的聚类效果更优。

另外，对比全连接矩阵聚类结果与k-近邻矩阵聚类结果，容易看出引入k-近邻后，在聚类决策上剔除了大量不相关点的影响，无论数据的规模大小与形状分布如何，每个数据点只考虑最近邻的k个数据点信息，排除了大量无关干扰，显然这是有利于聚类的。

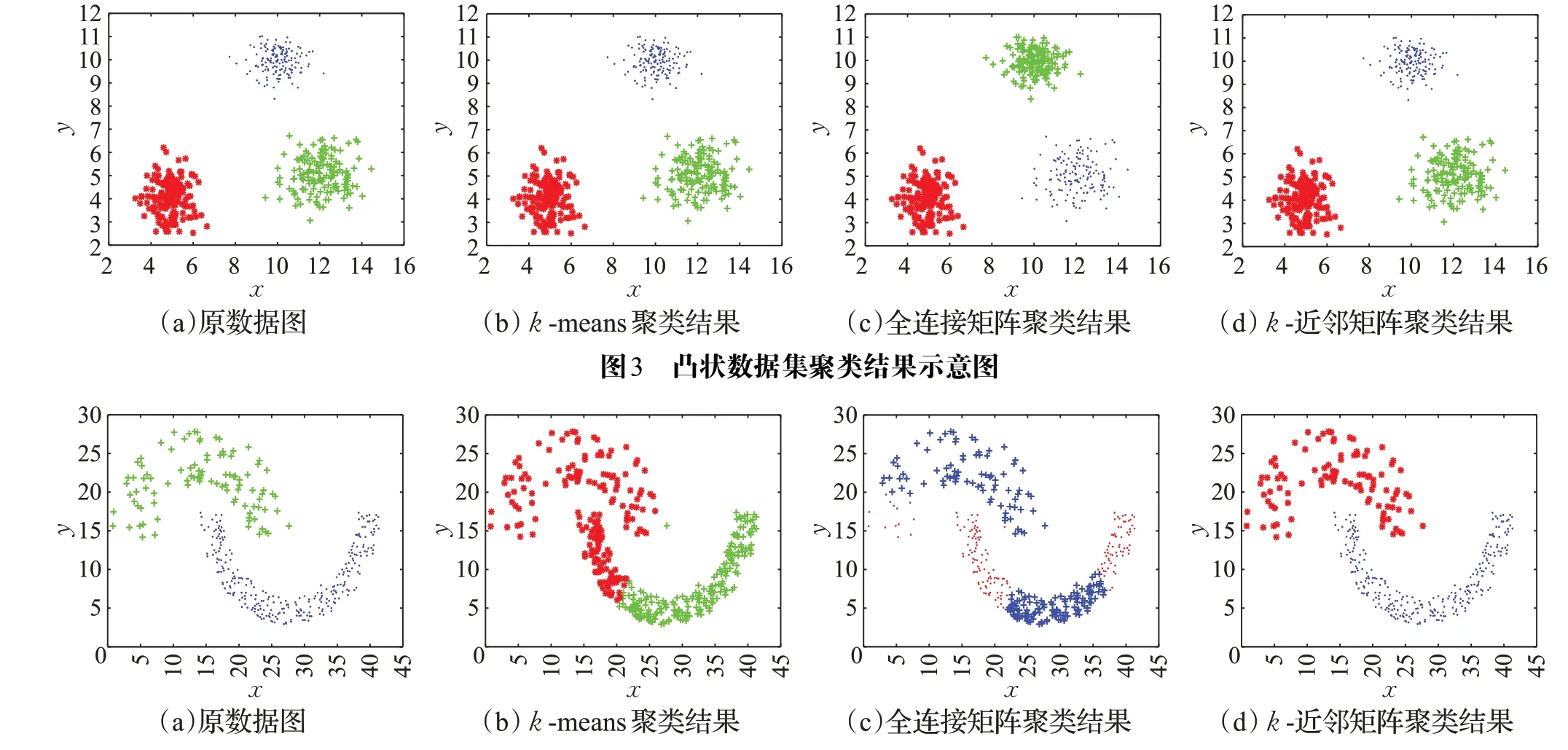
图4 双月数据集聚类结果示意图

图5 螺旋数据集聚类结果示意图

由此看来，k-近邻的距离信息对非凸数据集的聚类有更大的参考意义，在稀疏子空间聚类的研究中，可以使仿射矩阵有更理想的结构，有利于子空间分割。

3 模型建立及求解

3.1 模型建立

在前面的章节中，已经介绍了稀疏子空间聚类的核心问题是构造具有理想结构的仿射矩阵。接下来，对于给定的数据集X=(x1,x2,…,xn)∈Rd×n，本文在式（2）的基础上，根据前文所述，引入k-近邻思想，并利用数据点间的距离来辅助构造仿射矩阵A，得到本文的目标函数模型：其中，λ0与λ1是两个正则项参数，αi表示仿射矩阵A的第i列。目标函数模型第一项‖ XA-X利用仿射矩阵从整体刻画了数据系数表示的误差；第二项从整体约束了仿射矩阵的稀疏性；而模型第三项

3.2 模型求解

值得注意的是，在目标函数中存在约束条件Aij≥0与1,容易知道=1,因此是一个常数。所以问题（3）简化成问题（4）：

此时，原问题（3）中的参数λ0不用调节，这说明该模型本身就自带稀疏性。而参数λ1实质上在模型中调节着仿射矩阵A在“整体约束”和“局部约束”间的平衡。

接下来，针对问题（4），对A的每一列分别进行独立求解。由式（1），容易知道xi=Xαi=x1A1i+x2A2i+…+xiAii+…+xnAni，当约束Aii=0以及=0时，不妨将下标{j|xj∈Nk(xi)}重新记作{s1,s2,…,sk}，其中sm≠i(m=1,2,…,k)。于是，式（1）可以重新表示为xi=xs1As1,i+xs2As2,i+…+xskAsk,i。

为了描述方便，定义X-i=(xs1,xs2,…,xsk)∈Rd×k,=(As1,i,As2,i,…,Ask,i)T∈Rk×1，显 然 可 以 得 到 公 式另外定义邻接矩阵W，其中，显然邻接矩阵W是一个对称矩阵，即Wij=Wji，且主对角线元素Wii=0。同样地，用Wi∈Rn×1表示邻接矩阵W的第i列，用∈Rk×1表示Wi中第s1,s2,…,sk个元素组成的列向量。因此：

由此，式（4）可以重新写成问题（5）：

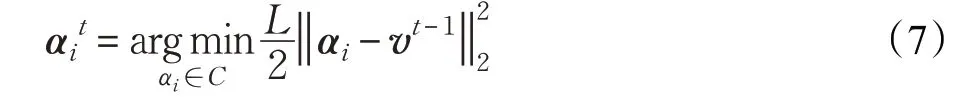
不难验证，式（6）和式（7）只相差一个恒值常数。

3.2.2 问题（8）的求解

容易知道，问题（8）的拉格朗日函数形式为：

因此，问题（8）的求解思路分如下两个步骤：

根据KKT条件（11）～（13），结合式（14）：

若ujt-1-＞0,由于φ∗j≥0,则则φ∗j=0，故

（2）更新迭代φ

由式（14），可以得到：

同理，根据KKT条件（11）～（13），结合式（16），可得：

值得说明的是，在算法过程中借用牛顿迭代法，因此显然是收敛的。为了加快算法的收敛速度，本文引入加速系数ct+1=(1+，并更新辅助变量

k-LS3C算法伪代码如下：

输入：数据集X=(x1,x2,…,xn)∈Rd×n，k，λ1。

输出：A=(α1,α2,…,αn)∈Rn×n。

1.初始化α1,α2,…,αn

2.计算邻接矩阵Wij=

3.for i=1,2,…,n do

4.计算idx(i)={j|xj∈Nk(xi)}

5.计算X-i=X(idx(i)),W(i,idx(i)),定义=αi(idx)

6.初始化β0i=αi及拉格朗日参数γ、φ

7.while不收敛do

9.固定φ，求解γ∗=

14.更新：t=t+1

15.endwhile

16.计算αi(idx)=

17.end for

4 实验

为验证本文提出的稀疏子空间聚类方法的有效性，本文选用经典聚类方法k均值（k-means）、规范划割（Normalized Cut，Ncut），以及经典子空间聚类方法LRR、SR、CLR_W（文献[31]中构造仿射矩阵的方法），与本文提出的方法k-LS3C进行比较，并从聚类准确率（Accuracy，Acc）、标准互信息（Normalized Mutual Information，NMI）、兰德指数（Rand Index，RI）等多个角度对聚类性能进行评价。用于实验的数据集有人造数据集、随机生成的子空间数据集、图像数据集以及真实数据集。其中，人造数据集选用了具有代表性的双月形和螺旋形数据集，图像数据集选取的是The Extended Yale Database B人脸数据库里的部分数据，真实数据集有iris、TOX-171、lung、australian以及crx数据集。

在参数设置方面，LRR、SR以及k-LS3C的正则参数λ取值为{0.000 1，0.001，0.01，0.05，0.1，1，10，100}；Ncut的σ取值为{0.001，0.01，0.1，1，10，100}；近邻点个数k取3～10。每个算法运行10次，取结果的最大值进行比较。实验相关环境为Microsoft Windows 7系统，处理器为Intel®CoreTMi5-3210 CPU@2.50 GHz，内存4.00 GB，采用编程软件Matlab R2015b。

4.1 评价指标

Acc是聚类最常用的评价指标，计算公式为：

其中，ri和si分别为聚类算法得到的类标签和数据真实的类标签；n为样本个数；δ(x,y)是一个函数，当x=y时δ(x,y)=1，否则δ(x,y)=0；map(ri)是一个排列匹配函数，将ri标签映射成与si匹配的等效标签。Acc的结果值在[0,1]之间，值越大越好。

NMI用于确定聚类的质量，计算公式为：

其中，ni表示聚类算法得到的每一类Ri(1≤i≤c)包含的数据点的个数；n̂j表示真实类别Sj(1≤j≤c)包含的数据点的个数；ni,j表示聚类算法结果Ri和真实类别Sj交集中包含的数据点的个数。NMI的结果值在[0,1]之间，值越大越好。

RI是一种用排列组合原理对聚类进行评价的方法，计算公式为：

其中，n为样本个数；a表示在真实类别Si的数据也隶属于聚类算法结果Ri的个数；d表示不在真实类别Si的数据也不属于聚类算法结果Ri的个数。RI的结果值在[0,1]之间，值越大越好。

4.2 人造数据集

本节选用双月形数据集和螺旋形数据集两个具有代表性的人造数据集来说明k-LS3C的有效性，同时探究近邻数k和正则化参数λ对聚类结果的影响。

双月形数据集是一类典型的非线性数据，形状像两个弯月，彼此嵌入于凹部，如图4（a）所示。由于双月形数据这种特殊分布，很多聚类算法非常容易将中间嵌入的地方混聚成一类。

螺旋形数据集是聚类算法研究中常用的一个数据集，由分布在3条螺旋曲线上众多数据点相互缠绕而成，如图5（a）所示。螺旋形数据整体看上去就像一个高斯圆，数据的相互缠绕也给聚类分析提出了更高的要求，因此想要得到较好的聚类效果，必须要合理地挖掘出数据的内部结构。

k-LS3C方法对双月形数据集和螺旋形数据集的聚类结果如图6所示。k-LS3C方法学习的邻接图如图7和图8所示。可以看出，k-LS3C方法对这两类数据集的聚类均能达到100%的准确率。实验中k-LS3C方法的运行时间较短，说明k-LS3C利用局部线性的思想明显提高了运算速度。

图6 k-LS3C对双月形及螺旋形数据集聚类结果

图7 双月形数据集邻接图

图8 螺旋形数据集邻接图

图9给出了k-LS3C在两个数据集上的仿射矩阵图，可以看出，k-LS3C得到的仿射矩阵有着良好的对角结构，而且从仿射矩阵图以及邻接图都可以看出，k-LS3C得到的仿射矩阵具有很好的稀疏性。这是因为模型中有‖ ‖A1项，同时由于Ai,j≥0，模型中的另一个正则项也可以看作是对仿射矩阵A再次施加了以为加权系数的l范数。l范数作11为l0范数的最优凸近似，很好地保证了仿射矩阵具有稀疏性。不过，从l1范数的定义可知，‖ ‖A1保证的其实是所有元素的绝对值之和最小。此时，约束条件中=0显然进一步加强了仿射矩阵的稀疏性。

图9 k-LS3C学习的仿射矩阵

图10～图13展示了参数k和λ对实验结果影响。图10和图11展示了邻近点个数k的选取对聚类准确率的影响。从实验结果可以看出，邻近点的个数k取得过小或者过大时，都会使得聚类的准确率降低，一般取5～10时效果较好。图12和图13展示了参数λ对聚类准确率的影响。从实验结果可以看出，当确定了合适的k值后，参数λ对聚类结果的影响不大。这是因为当k值确定后，等效于从局部对模型进行了约束，此时从一定程度上代替了参数λ的调节功能。

图10 双月形数据集上k对聚类精度的影响(λ=1)

图11 螺旋形数据集上k对聚类精度的影响(λ=1)

图12 双月形数据集上λ对聚类精度的影响(k=7)

图13 螺旋形数据集上λ对聚类精度的影响(k=4)

因此，基于k-LS3C模型具备这样的特点，在进行调参工作时，首先应寻找合适的参数k。由于近邻数k是整数，因此寻找起来难度不大，根据经验，一般在5～10之间寻找，可以根据数据集特点灵活调整。如果数据集分布较散，类簇间距离较开，参数k可以适当选择大点。如果数据集分布较密，类簇间距离较近，参数k可以适当选择小点。当确定了合适的参数k后，再对参数λ进行调节，遵循一般的调参方式即可。总体来说还是比较容易能够调到合适的参数，得到理想的聚类结果。

4.3 随机独立子空间

依照文献[32]的方法，首先构造5个相互独立的线性子空间，其中5个基矩阵由Ui+1=TUi(i=1,2,3,4)生成，T表示一个随机旋转矩阵，U1∈R100×100是一个随机列正交矩阵，因此每个子空间都是100维的。若每个子空间里面由Xi=UiCi产生20个样本，则得到的数据矩阵是X=[X1,X2,X3,X4,X5]∈R100×100,其中C1∈R100×20为独立同分布的标准高斯矩阵。

实验结果表明，当k取5到10的任意整数，λ取{0.001，0.005，0.01，0.05，0.1，0.5，1}中的任意参数时，k-LS3C算法的准确率均为100%。

4.4 人脸数据库聚类

The Extended Yale Database B人脸数据库，其包含了38个人的2 414张人脸前额图像，每一个人都有59～64张在不同的实验室可控光照条件下的人脸图像，部分人脸图像被严重的“阴影”污染。如图14所示。每幅人脸灰度图像的分辨率大小是192×168，为减小算法的计算时间和存储空间，首先将所有图像的分辨率重新调整为32×32，并将像素值规范化到[0,1]区间。

图14 图像数据集部分样本图像示例

本文使用The Extended Yale Database B数据库中的前20类的人脸图像，选取每类中的10张图像，总共200张。本文模型中没有考虑误差，因此尽量选用噪声比较少的图像来进行实验。把每张图像转换为1 024维行向量，形成数据矩阵X∈R200×1024。k-LS3C对该数据集的聚类结果如图15所示。

4.5 真实数据集

本文采用5个常用的UCI真实数据集进行实验，分别是iris、TOX-171、lung、Australian以及crx数据集，数据集的描述如表1所示。表2～表4分别采用Acc、NMI以及RI指标评价了不同算法在这些数据集上的聚类结果。表中，数据加粗代表算法性能最优，数据加下划线代表算法性能次优。

可以看出，本文提出的k-LS3C算法具有良好的聚类结果，在实验的5个数据集以及3种评价指标上，基本都表现出比k-means、Ncut、CLR_W、LRR以及SR更优的性能。这主要是因为k-LS3C构造的仿射矩阵更加合理，从整体和局部两个角度综合考虑，能够寻找出数据的潜在结构，得到更好的子空间划分。

表1 真实数据集描述

表2 不同算法在各数据集下的Acc比较

表3 不同算法在各数据集下的NMI比较

表4 不同算法在各数据集下的RI比较

4.6 含噪数据集

图15 k-LS3C对图像数据集的聚类结果(Acc=90.88%)

为了测验k-LS3C算法对含噪数据集的鲁棒性，构造子空间的典型数据集，如图16所示。该三维数据集由一个二维平面和一条一维直线所组成，由图16（b）可以看出，数据点处于完全的平面或直线内。k-LS3C算法对其聚类结果如图18（a）所示，聚类准确率为100%。但由于现实生活中，数据会含有些许噪声，可能呈现如图17所示的样子。图17（b）显示数据点不完全处于平面或直线内，此时k-LS3C算法依然能准确聚类，如图18（b）所示。这是因为k-LS3C算法综合考虑了数据分布的整体和局部，尤其是在引入k近邻后，噪声对数据点局部间的相似紧密-疏离关系影响不大，换而言之，即便存在少量噪声，一般也不会影响到数据间的亲疏关系。通过这样的机制能够加强模型的稳定性，因此k-LS3C算法对含噪数据具备良好的鲁棒性。

图16 子空间数据集示意图

图17 含噪子空间数据集示意图

5 结论和展望

图18 k-LS3C对数据集的聚类结果

本文提出了一种全新的子空间聚类方法k-LS3C，在构造仿射矩阵的过程中，引入了k-近邻思想，并基于图论知识设计了合适的正则项，不仅加强了数据局部信息的利用，也使仿射矩阵向相似矩阵的过渡更加合理自然。在多种数据集上与目前流行的稀疏子空间聚类算法进行了对比，结果证明本文算法能够得到更优的聚类结果。下一步，将继续研究如何根据数据分布结构自适应地确定近邻数k值。另外，在模型中对误差进行更细致的考虑也是今后研究的一个方向。