Dynamic soil-structure interaction analysis in time domain based on a modified version of perfectly matched discrete layers

Dong Van Nguyen, Dookie Kim

Department of Civil Engineering, Kunsan National University, 558 Daehak-ro, Gunsan-si, 54150, Republic of Korea

Keywords:Soil-structure interaction Time domain Wave propagation Wavelength Infinite domain Perfectly matched discrete layer (PMDL)

A B S T R A C T Analysis of soil-structure interaction is commonly conducted by dividing the infinite domain of the soil into two domains:interior and exterior domains.The interior domain is bounded in a small region,while the exterior domain is replaced by artificial boundary conditions. The choice of artificial boundary conditions is a critical issue in the analysis of soil-structure interaction problems. Perfectly matched discrete layer (PMDL) has been proved as a good approach for modeling the exterior domain. In this study, a modified version of the PMDLs, i.e. PMDLs with analytical wavelengths (AW-PMDLs), is used in the soil-structure interaction analysis in time domain,which essentially can be regarded as an extension of the analysis in frequency domain, being previously proven to be effective. Numerical verifications are implemented. The results demonstrate that the proposed method performs well in the analysis of soilstructure interaction problems in time domain.

1. Introduction

Wave propagation in unbounded domains is considered as a basic component of dynamic analysis of soil-structure interaction. The spurious reflection needs to be reduced when the waves impinge on the boundaries in order to obtain good results.The simplest way to tackle the problem is to use a truncation far away from the computational region. In this case, the soil model is usually very large, thereby making the analysis a bit prohibitive.

To reduce the size of a soil-structure interaction problem, the soil is divided into interior and exterior domains (see Fig.1). Usually, the exterior domain is replaced by artificial boundary conditions which thereby render the infinite domain to be a finite domain (the interior) with artificial boundary conditions.

Many kinds of artificial boundary conditions have been proposed, such as the boundary element method (BEM) (Hall and Oliveto, 2003), coupled finite element method (FEM) and BEM(FEM-BEM) (Von Estorff, 1991), viscous boundaries (Lysmer and Kuhlemeyer, 1969), transmitting boundaries (Lysmer and Drake,1971; Lysmer and Waas, 1972; Kausel, 1974), infinite elements(Kim and Yun, 2000; Yun et al., 2000; Yang et al., 2015), perfectly matched layers (PMLs) (Berenger, 1994; Basu and Chopra, 2004),and perfectly matched discrete layers (PMDLs) (Guddati and Tassoulas, 2000; Guddati and Lim, 2006).

Each artificial boundary condition has its own advantages and limits.In BEM,only the boundary needs to be discretized,and it is thereby more effective in terms of computational resources in some cases. However, compared with FEM, BEM requires more knowledge about fundamental solutions to the partial differential equations, which leads to difficulties for engineers to apply the BEM in practice due to the most general use of FEM in commercial software. For viscous boundary, it is one of the most commonly used methods due to its simplicity. It works effectively when the interior domain of the soil medium is large enough to reduce the incident angles of the waves at the boundaries. In Abaqus(Dassault Systemes Simulia Corporation,2014), an equivalent type of viscous boundary, i.e. infinite element, is available. It has the same merits and disadvantages with respect to the viscous boundary. This kind of boundary condition has been applied in many studies (Hokmabadi and Fatahi, 2016; Van Nguyen et al.,2016, 2017; Fatahi et al., 2018). The results obtained by using the infinite elements in Abaqus will be compared with the proposed method in this paper. Viscous boundary and infinite elements belong to the types of local boundary conditions,which are local in both space and time domains. They are known as approximate solutions for boundary conditions, but they are easy

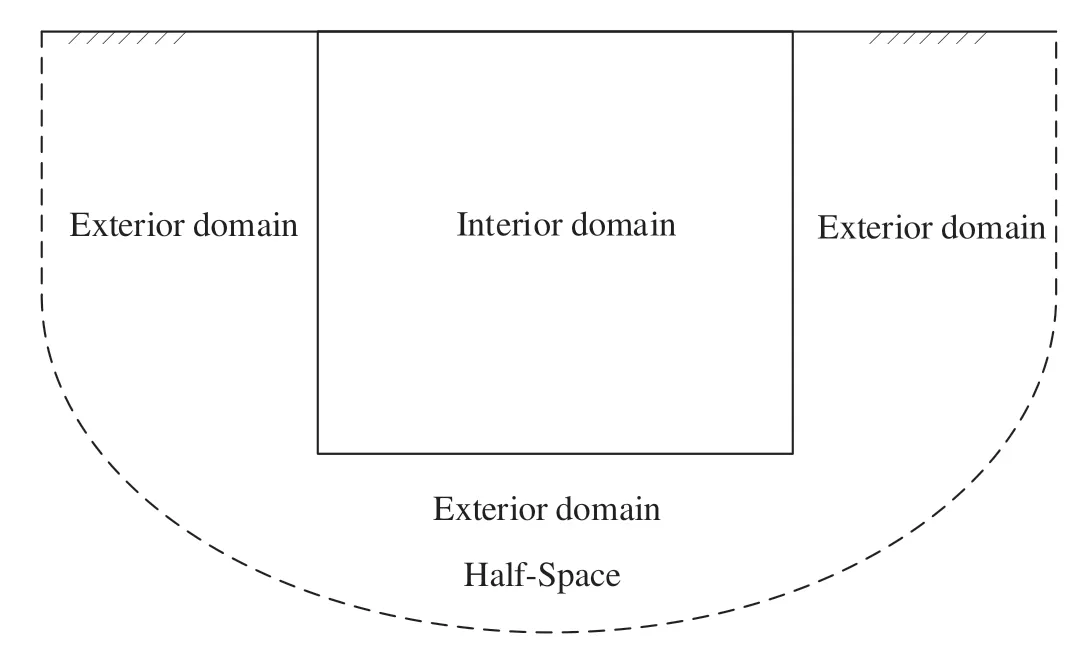
Fig.1. Soil-structure interaction system.

2. Perfectly matched discrete layers with analytical wavelengths

In this section, the determination of the lengths for AW-PMDL elements in the time domain is discussed. The procedure is the same as the one in the frequency domain (Van Nguyen and Kim,2018). For a soil medium (Fig. 2a), the application of the AWPMDL elements is shown in Fig. 2b. The AW-PMDLx, AW-PMDLz,and AW-PMDLxz are applied for the vertical edge,horizontal edge,and corner, respectively.

For the edge elements (AW-PMDLx and AW-PMDLz), there are two types: Types 1 and 2. Type 1 elements have pure imaginary lengths in order to absorb the propagating waves effectively.Type 2 elements with real lengths are used to absorb the evanescent waves.

The lengths of Type 1 AW-PMDLx and AW-PMDLz elements are calculated as follows:to be implemented. On the other hand, the global boundary conditions like transmitting boundaries are completely coupled in space and time domains. They are exact solutions, but are cumbersome. In addition to the local and global boundary conditions, there is another type of boundary condition called material-based boundary condition, for instance, PML. The principle of the PML is based on a special absorbing medium. One of the major advantages of the PML is its simple implementation.The noticeable drawbacks of PML are the presence of discretization and truncation errors. By combining the advantages of the local boundary condition and PML, PMDL is developed subsequently.

PMDL is one of the most efficient methods to solve soil-structure interaction problems. It is originally known as continued fraction absorbing boundary condition (CFABC) (Guddati and Tassoulas,2000), which combines the advantages of two methods, i.e. local absorbing boundary condition(ABC)and PML.The accuracy of local ABC and the flexibility of PML are both taken into consideration in the PMDL. The presence of real and imaginary lengths together allows the PMDL to absorb both propagating and evanescent waves.One of the key factors of the PMDL is the use of mid-point integration rule in order to eliminate the discretization error (Guddati and Tassoulas, 2000). The power of the PMDL method has been proved by many studies,such as time harmonic wave propagation in discretized domains (Thirunavukkarasu and Guddati, 2011),scalar wave propagation (Guddati and Lim, 2006), and static analysis (Savadatti and Guddati, 2010).

In the recent work by Van Nguyen and Kim(2018),the authors proposed a modified version of the PMDLs, i.e. perfectly matched discrete layers with analytical wavelengths (AW-PMDLs). The method was applied in the frequency domain with a different strategy to determine the parameters, and the effectiveness and accuracy of the method were demonstrated; furthermore, the computational effort is reduced considerably.

However, to solve the problem in time domain with the AWPMDLs, there still exist some problems due to the presence of the imaginary lengths. The procedure to deal with the boundary conditions in a direct integration algorithm based on real numbers is not clear either. Therefore, the proposed method of AW-PMDL is developed, verified, and applied to the time domain for soilstructure interaction analysis with a clear algorithm. First, the determination of AW-PMDLs parameters is shown.Second,for the sake of the application of AW-PMDL elements in the time domain,a finite element algorithm is presented to derive the dynamic stiffness of the AW-PMDL elements. Third, numerical analyses are provided to verify the proposed method in the time domain, and finally, the conclusions are made.

where V is the wave (S- and P-wave) velocity, and the values of θjsatisfying 0 ≤θj＜π/2 are chosen as follows:

where n′is the layer number of Type 1 elements.

The lengths of the Type 2 elements are real and related to the wavelengths of the problem (λxand λz):

where Vsis the S-wave velocity;and fxand fzare the horizontal and vertical natural frequencies of the soil medium,respectively,which are derived as follows (Rowe, 2012):

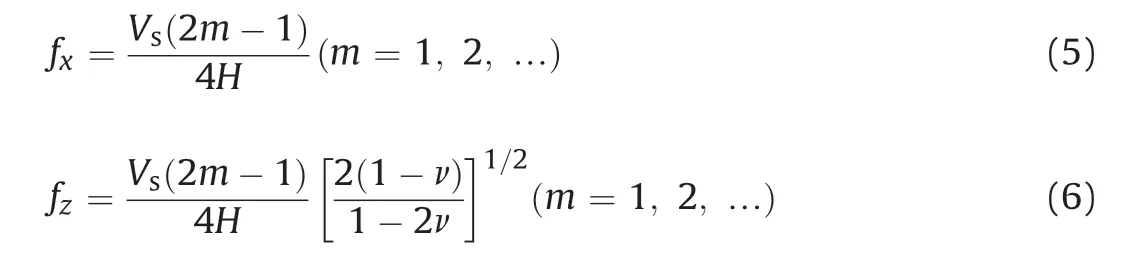
where m is the mode numbering of the problem,ν is the Poisson's ratio, and H is the truncated depth of the soil medium (Fig. 2).

From Eqs. (3)-(6), we obtain

In the case of the corner elements(AW-PMDLxz),which are the tensor products of the AW-PMDLx and AW-PMDLz elements, their lengths in each direction are taken from the corresponding edge elements in the same directions.

3. Finite element algorithm

Fig. 2. Application of AW-PMDL elements to a half-space problem. (a) Original half-space problem; and (b) Model with AW-PMDL elements.

Fig. 3. Finite elements and AW-PMDL elements.

One of the most important characteristics of the PMDL and AWPMDL elements is the application of mid-point integration in order to eliminate the discretization error. As shown in Fig. 3, in the model with the AW-PMDL elements, there are four types of integration rules: 2 × 2 integration (finite elements in the interior domain),1×2 integration(AW-PMDLx elements),2×1 integration(AW-PMDLz elements), and 1 × 1 integration (AW-PMDLxz elements).

In this study, the dynamic stiffness of a rectangular AW-PMDL element is evaluated by applying the Gauss rule (Weaver and Johnston, 1984; Cook, 2007) with physical and natural coordinates shown in Fig.4a,b,respectively.The dynamic stiffness of the element is defined as follows:

S = K +iωC-ω2M (9)

where K, M and C are the stiffness, mass, and damping matrices,respectively; and ω is the excitation frequency.

According to Lee et al. (2014), the stiffness matrix K and mass matrix M of the rectangular element in Fig. 4 are obtained as follows:

where ρ is the mass density, and N is the shape function matrix.

Fig. 4. A rectangular AW-PMDL element: (a) Physical coordinate, and (b) Natural coordinate.

The elasticity matrices for plane strain conditions are given by

where λ and μ are the Lame constants, which can be written as

where E is the elastic modulus.

The shape function matrix N in Eq.(11)is of the following form:

where the shape function Njis expressed as follows:

The strain-displacement matrices are achieved through the following definitions:

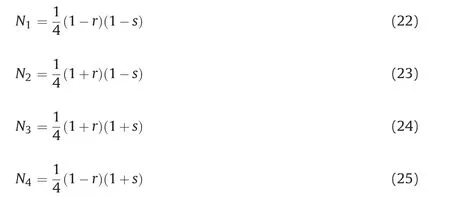
In this study, Rayleigh damping is used in the time domain analysis, which is defined as (Chopra, 2001):

C = αM+βK (26)

where α and β are the mass and stiffness proportional coefficients,respectively.

The values of α and β are determined using the damping ratios of two different natural modes m and n.Usually,the same damping ratio (ξ) is assumed for both modes, and then we have

where ωmand ωnare the natural frequencies of modes m and n,respectively.The results of the problems in the time domain are influenced by the frequencies selected to define the damping coefficients (α and β) in Eqs. (27) and (28). There have been some studies examining the use of Rayleigh damping in the time domain(Park and Hashash,2004; Hall, 2006; Tyapin, 2016). In the work of Park and Hashash(2004), the authors suggested a procedure to choose the natural frequencies to obtain the damping coefficients for a soil medium:the first frequency is the first natural frequency of the soil medium and the second one is the frequency that agrees with the predominant frequency of the excitation motion.

In a soil medium, the damping is usually represented by hysteretic damping.This kind of damping is independent of frequency and used to define the complex stiffness of models.For that reason,the hysteretic damping is easy to be implemented in the frequency domain. However, in the time domain, it needs to be converted to Rayleigh damping for the sake of applications.According to Soroka(1949), if the values of damping are small (i.e. hysteretic damping factor η ≤20%), the relationship between the hysteretic damping factor(η) and the Rayleigh damping ratio (ξ) can be expressed as

For an AW-PMDLz element with the wave velocity Vzand the corresponding length 2b = -2iVz/(ω cosθj)， the dynamic stiffness is given as

ξ = η/2 (29)

For evanescent waves, the lengths of the AW-PMDL elements are real;therefore,the dynamic stiffness S in Eq.(9)is formed with the same ordinary finite elements except using the mid-point integration rule. However, for propagating waves, the lengths of the AW-PMDL elements are imaginary. To make use of the AWPMDL elements in the time domain, some modifications are needed. From Eqs. (9)-(11) with the wave velocity Vxand corresponding length 2a = -2iVx/(ω cosθj)， the dynamic stiffness matrix of an AW-PMDLx element is expressed as follows:

In the case of an AW-PMDLxz element,if at least one length,2a or 2b, is real, the procedure to determine the dynamic stiffness is similar to that of the edge elements(AW-PMDLx and AW-PMDLz).However, if both of the lengths (2a and 2b) are imaginary, i.e.2a = -2iVx/(ω cosθj) and 2b = - 2iVz/(ω cosθj′)， the dynamic stiffness should be updated as

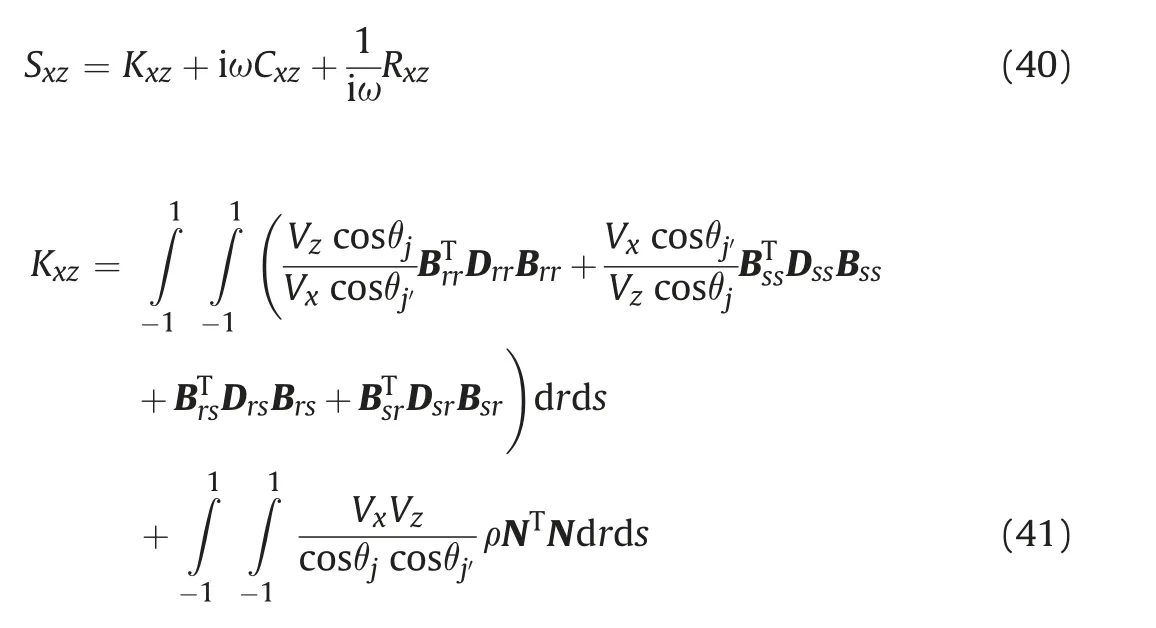
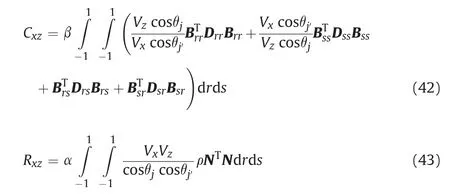
The equation of motion of the system, including the interior finite elements and the AW-PMDL elements,is written in the time domain (Guddati and Lim, 2006) as follows:

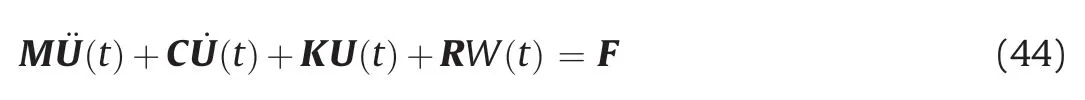
where ¨U(t)， ˙U(t) and U(t) are the acceleration, velocity, and displacement vectors, respectively; and W = ∫Udt is the integration of displacement U. In the case of the AW-PMDL elements, the values of M,C,K,and R matrices are obtained from Eqs.(30)-(43).In this paper,the AW-PMDL elements are implemented as userdefined element (UEL) subroutines in Abaqus (Dassault Systemes Simulia Corporation, 2014) using the implicit algorithm. In the subroutine for an AW-PMDL element, properties, original coordinates of the nodes, and nodal displacements are given, while the right-hand-side vector of the residual and the Jacobian matrix of the element must be defined.

Fig. 5. Block on a homogeneous half-space soil medium problem.

4. Numerical verifications

4.1. Dynamic analysis of a block on a homogeneous half-space soil medium

In this section,an elastic block on a homogeneous half-space soil medium is considered(Fig.5).As shown in the figure,the block has a width of 2b=8 m,and a height of h=12 m.Two cases of loads are applied at the top of the block: the vertical impulse load (Pv) and the horizontal impulse load(Ph).The function of the impulse loads is given in Fig. 6. The material properties of the block and soil medium are shown in Table 1. Two elastic modulus of the soil are considered: ES= EB/3 and ES= EB.

The half-space soil is modeled by using 16×30 finite elements in the interior domain and AW-PMDL elements in the exterior domain (Fig. 7). The AW-PMDL elements are applied as UEL in Abaqus. A similar model as the AW-PMDL model, i.e. the same interior region,is implemented.In this model,the infinite elements(CINPE4), which are available in Abaqus, are used instead of the AW-PMDL elements.

In addition to the analysis of applied AW-PMDL and infinite elements models, an extended model with large dimensions is examined as well.

The dimensions of the extended model are chosen large enough so that the model can be considered to attenuate effectively the wave propagation. The width and height of the soil stratum of the extended model are 100b=400 m,and 50b=200 m,respectively.The model includes 200 × 100 finite elements. The base of the extended model is fixed and the lateral boundaries are free.

Due to the convergence characteristics, the accuracy of the numerical problems will reach a certain level when the number of the AW-PMDLs elements is increased to a certain value.In this study,11 layers of AW-PMDLs are used to simulate the exterior domain of the soil media for all the numerical verifications: two layers of Type 1(Eq.(1))and nine layers of Type2(Eqs.(7)and(8)with m=1,2,…,9).

Fig. 6. Load function for Pv and Ph.

The horizontal and vertical displacements at point A of the block due to the distributed horizontal and vertical loads are examined, respectively. The time-history displacements of the AW-PMDL,infinite elements,and extended models are shown in Figs. 8 and 9, where the results obtained by Von Estorff (1991)are also provided as a reference solution. In the reference solution, BEM and FEM were applied. The displacements areplotted against dimensionless time defined as t0= tVs/b. It can be seen that the results of the proposed method, the infinite elements model, the extended model, and the reference solution have a good agreement. However, there are some differences between the infinite elements and the AW-PMDL models. The reason is that the behavior of the infinite elements in Abaqus is similar to the one of the viscous boundaries, and they do not absorb perfectly the propagating waves when the interior region is small.

Table 1 Material properties(block on a homogeneous half-space soil medium problem).

Fig. 7. Block on a homogeneous half-space soil medium with AW-PMDLs application.

4.2. Dynamic analysis of a block on a layered soil medium over half-space

In order to examine the effectiveness of the proposed AW-PMDL method in a layered soil medium over half-space, we consider a problem with an elastic block as shown in Fig.10.The dimensions of the block and the applied external loads are the same as the one mentioned above for the homogeneous soil medium.

The soil medium includes two layers: the first one is 4 m thick and the second one is a half-space layer. Table 2 shows the properties of the block and two soil layers.The elastic moduli of the two soil layers will be taken based on the relations: E1= EB/3 and E2=10E1.

In the built AW-PMDL model (Fig.11), the number of finite elements of the interior domain is 16×30 for the soil layers and 4×6 for the block. The AW-PMDL elements are implemented using the UEL in Abaqus.

Fig. 8. Displacements at point A of the block on a homogeneous half-space soil medium problem (ES = EB/3). (a) Vertical displacements due to a vertical load; and (b) Horizontal displacements due to a horizontal load.

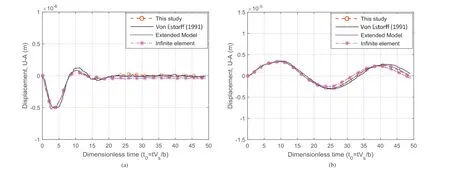
Fig. 9. Displacements at point A of the block on a homogeneous half-space soil medium problem (ES = EB). (a) Vertical displacements due to a vertical load; and (b) Horizontal displacements due to a horizontal load.

Fig.10. Block on a layered soil medium over half-space problem.

Corresponding infinite elements (CINPE4) and extended models are analyzed so as to make a comparison with the proposed method of AW-PMDLs. In the case of the infinite elements model, the interior domain is kept the same as that in the AWPMDL model. The characteristics of the extended model are the same as those in the previous section: the width of the soil medium is 100b=400 m,the height is 50b=200 m,and the number of finite elements for the soil medium is 200×100.The fixed base and free lateral edges are applied as the boundary conditions of the model.

The vertical and horizontal displacements at point A are calculated, respectively. The results of the AW-PMDL model,infinite elements model, and the extended model are presented together with a reference solution obtained by Kim and Yun(2000) in Fig. 12. In the reference solution, the authors implemented analytical frequency-dependent infinite elements for theexterior domain. The dimensionless time in the figure is decided as t0= tVs1/b， where Vs1is the shear wave velocity of layer 1.Clearly, the AW-PMDL elements have a good behavior for a layered soil medium.

Table 2 Material properties (block on a layered soil medium over half-space problem).

Fig.11. Block on a layered soil medium over half-space with AW-PMDLs application.

Fig.12. Displacements at point A of the block on a layered soil medium over half-space problem. (a) Vertical displacements due to a vertical load; and (b) Horizontal displacements due to a horizontal load.

4.3. Dynamic analysis of a tunnel in a homogeneous half-space soil medium

In this section, a tunnel system is considered with the traffic load applied on the bottom of the tunnel(Fig.13).The traffic load is presented as a distributed vertical load(P)with the load function of time as shown in Fig.14.The material properties of the tunnel and soil are given in Table 3. The responses of two points will be examined: point A at the bottom of the tunnel and point B at the ground surface (Fig.13).

Fig.13. Tunnel in a homogeneous soil medium over half-space problem.

Fig.14. Load function for vertical load P.

Table 3 Material properties (tunnel in a homogeneous half-space soil medium problem).

Fig. 15. Tunnel in a homogeneous half-space soil medium with AW-PMDLs application.

The AW-PMDL elements are applied for the exterior domain of the soil medium as shown in Fig.15.The number of finite elements in the interior domain is 40 × 50 and the element size is 0.5 m × 0.5 m. Similar to the previous sections, the infinite elements and extended models of the problem are analyzed as well.The dimensions of the extended model are chosen to be very large(i.e.80b×80b=200 m×200 m).The number of finite elements of the extended model is 400 × 400 with an element size of 0.5 m × 0.5 m.

The vertical displacements at points A and B are plotted against the dimensionless time t0= tVs/b.The results of the three models(the AW-PMDL, the infinite elements, and the extended models)are compared with the reference solution of Von Estorff and Antes(1991) obtained by using hybrid method combining the FEM and BEM.Fig.16 indicates that the proposed AW-PMDL elements have a good implementation.

4.4. Dynamic analysis of a tunnel in a layered soil medium over half-space

In this section,the effectiveness of the proposed method in the time domain is examined by analyzing a tunnel system in a layered soil medium over half-space(Fig.17).The traffic load at the bottom of the tunnel is the same as the one in the homogeneous soil case(Fig.14). The properties used for the system are shown in Table 4.The vertical displacement at point A is monitored for two cases based on the ratio of the elastic modulus between two layers:case 1(E2= 2E1) and case 2 (E2= 5E1).

Fig.18 shows the truncated model with the AW-PMDLs application. The number of finite elements in the interior domain is 40×50.The size of the elements shown in Fig.18 is 0.5 m×0.5 m.A similar infniite elements(CINPE4)model is considered.Then,an extended model with the same element size as that in the AWPMDL model (0.5 m × 0.5 m) is chosen. The number of finite elements of the extended model is 400×400 and the dimensions are considered large enough for the wave propagation problem: the width of the model is 80b=200 m,and the height is 80b=200 m as well.

The responses at point A are shown in Fig. 19, including the results of the AW-PMDL model, the infinite elements model, the extended model,and the reference solution of Kim and Yun(2000).The dimensionless time is defnied as t0= tVs1/b.The results show that the AW-PMDL elements perform very well.

Fig. 16. Vertical displacements of the tunnel in a homogeneous half-space soil medium problem. (a) Vertical displacements at point A; and (b) Vertical displacements at point B.

4.5. Computational time

In this section, the computational time of different models as discussed above is calculated and compared. Since the computational time of previous studies (Von Estorff,1991; Vos Estorff and Antes,1991;Kim and Yun,2000)was not given,the comparison is made only between the proposed model (AW-PMDL elements),the infinite elements model, and the extended model. A personal computer with 3.4 GHz CPU is used to analyze all the models. The comparison of the total computational time is presented in Table 5.

It can be easily found that the computational time of the proposed model (AW-PMDL elements) is the smallest compared with the infinite elements and the extended models, and the computational time of the extended model is more than the others. In this study,the proposed model has similar interior domain to that of the infinite elements model. For that reason, although the computational time of the proposed method is still smaller than that of the infinite elements model, its difference is not marked.However, in general, if the models use the infinite elements to reach the accuracy as the AW-PMDLs model does, their interior domains need to be further extended, which would in turn cause the increase of the computational time. Therefore, the proposed method with AW-PMDL elements is effective in terms of computational cost as well.

Fig.17. Tunnel in a layered soil medium over half-space problem.

Table 4 Material properties(tunnel in a layered soil medium over half-space problem).

Fig.18. Tunnel in a layered soil medium over half-space with AW-PMDLs application.

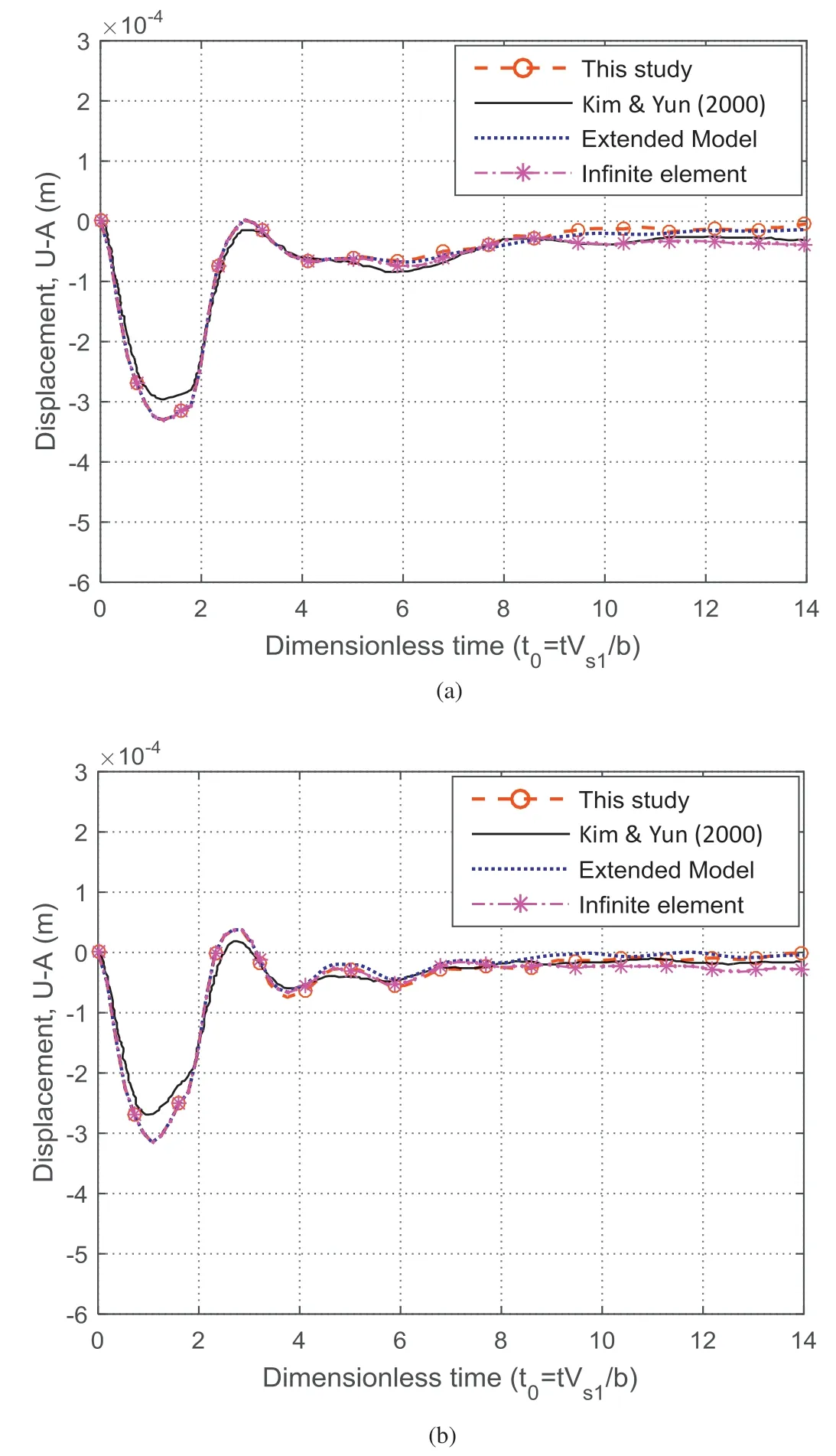
Fig.19. Vertical displacements at point A of the tunnel in a layered soil medium over half-space problem: (a) E2 = 2E1, and (b) E2 = 5E1.

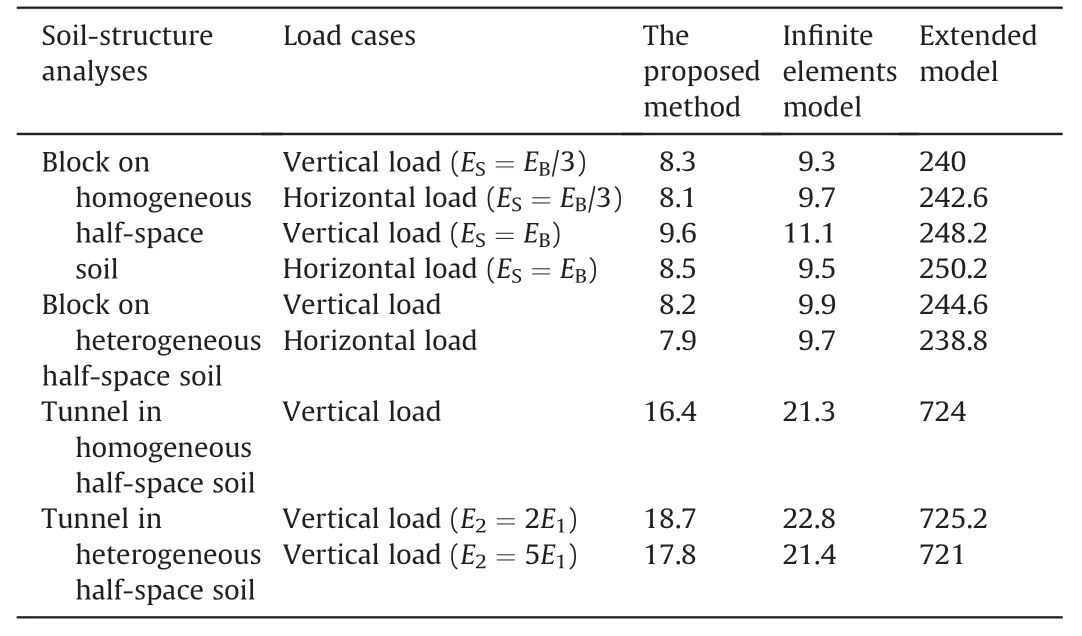
Table 5 Total computational time (s) for soil-structure interaction analyses.

5. Conclusions

In this study,a procedure was given to apply AW-PMDLs in the time domain for soil-structure interaction analysis. The procedure was developed based on the AW-PMDL elements in the frequency domain,which was proposed recently.For the sake of application of the AW-PMDL elements in the time domain, a finite element algorithm was presented. The algorithm was implemented by using the UEL in Abaqus. It was demonstrated that the AW-PMDL elements are applied easily for the exterior domain in the time domain.Numerical verifications with application of the AW-PMDL elements were analyzed for the models of a block and a tunnel on homogeneous and layered soil media.The results showed that the proposed AW-PMDL elements are effective and accurate in the time domain. The present AW-PMDLs can be extended to nonlinear applications and earthquake loading problems as well. Furthermore, three-dimensional version of AW-PMDLs is a promising problem in the future.

Declaration of Competing Interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgments

This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade,Industry and Energy(MOTIE)of the Republic of Korea(Grant No.20171510101960).