Multi-scale modelling of gas flow in nanoscale pore space with fractures

Qingrong Xiong, Diansen Yang, Weizhong Chen

a Research Centre for Radwaste&Decommissioning and Modelling&Simulation Centre,Dalton Nuclear Institute,University of Manchester,Manchester,M13 9PL,UK

b School of Mechanical, Aerospace and Civil Engineering, University of Manchester, Manchester, M13 9PL, UK

c State Key Laboratory of Geomechanics and Geotechnical Engineering,Institute of Rock and Soil Mechanics,Chinese Academy of Sciences, Wuhan,430071, China

d University of Chinese Academy of Sciences, Beijing,100049, China

Keywords:Pore network Nanopores Apparent gas permeability Callovo-Oxfordian (COx) claystone

A B S T R A C T In this work,a multi-scale pore network with fractures is developed against experimental data in a wide range of degrees of water saturation. The pore network is constructed based on the measured microstructure information at several length scales. The gas transport is predicted by different gas transport equations (e.g. Javadpour, dusty gas model (DGM), Civan and Klinkenberg), which can consider the fundamental physics mechanisms in tight porous media, such as Knudsen diffusion and viscous flow.Then, the model is applied to simulating the gas permeability of the Callovo-Oxfordian (COx) claystone.The predicted gas permeability is basically in good agreement with the experimental data under different degrees of water saturation. Then the effects of micro-fissures are studied. The results suggest that this model can predict the gas flow in other tight porous media as well and can be applied to other fields such as carbon capture and storage.

1. Introduction

Understanding gas transport and predicting effective transport properties (permeability, effective diffusivity, etc.) in tight porous media are of paramount importance for practical applications,such as in shale gas reservoirs and nuclear waste disposal projects(Chen et al.,2015a),where the main pore size is in the range of 1-200 nm.

As gas transport in nanopores involves several flow mechanisms(e.g. viscous flow, Knudsen diffusion and molecular diffusion), it cannot be described by the Darcy equation (Darabi et al.,2012). In this sense, many modelling approaches, such as the molecular dynamics (MD) method, direct simulation Monte Carlo (DSMC)method, and lattice Boltzmann method (LBM), have been developed to describe gas flow in nanopores.MD and DSMC methods can accurately describe the exact forces between molecules (Bird and Brady, 1994; Karniadakis et al., 2006). However, they cannot be used for systems larger than a few microns due to the requirement of significant computation resources. LBM is an efficient method which can be used to simulate gas flow in relatively large porous media, but it fails to account for the high-order terms (Zhao et al.,2016). In addition, although LBM is a Navier-Stoke equation solver,some LBM models are not suitable for gas flow simulation in porous media when the Knudsen number, i.e. ratio of molecular mean free path to the characteristic length of porous medium, is larger than 0.1. Since the non-continuum effect becomes more pronounced with increase in Knudsen number (Tang et al., 2005;Chai et al., 2010), some models are sound to simulate gas flow under any Knudsen numbers. Nevertheless, the specific velocity distributions in the porous media cannot be obtained as they are not based on the kinetic theory(Chen et al.,2015a,b).Pore network model is one of the promising approaches due to its computation efficiency,and can represent a larger volume that has been used to simulate reactive multiphase flow in porous media based on realistic representation of the microstructure of the porous media(Xiong et al.,2015, 2016).

In ultra-tight porous media,the measured pores are usually in the range of 1-100 nm (Yang et al., 2013; Song et al., 2015, 2016;2017; Xiong and Jivkov, 2018). However, the fractures are usually above micrometre scales. Thus, a multi-scale network model would be helpful in predicting the permeability of porous media where (micro-) fractures are included. However, fewer multiscale pore networks have been developed to simulate the gas flow in nanopores with micrometre fractures to the authors'knowledge.

In this work, we developed a new pore network model on two length scales in three dimensions. One represents nano-scale system, and the other exists in the nanopore regions. The Callovo-Oxfordian (COx) claystone is possibly a candidate as host rock for high-level radioactive nuclear waste repository, which is characterised with pores in the range of nanometres. In this case, it is chosen for illustration. Next, a pore network is constructed to represent the measured microstructure characterisation of the COx claystone.Then it is combined with various gas transport equations(Darcy equation, the dusty gas model (DGM), Civan model and Javadpour model) for gas transport simulation. Finally, the predicted apparent gas permeability is compared with experimental data under different degrees of water saturation to illustrate the accuracy of different models.

2. Experimental data

The particle density of the COx claystone specimens sampled at 490-560 m depth is about 2.72 g/cm3and the apparent density is approximately 2.4 g/cm3in natural state (Yang et al., 2013). The total porosity of the COx claystone varies between 12% and 18%with 10% macroporosity (＞50 nm), 86% mesoporosity (2-50 nm)and 4% microporosity (＜2 nm) (M'Jahad, 2012). The pore size distribution of the COx claystone has been characterised by the mercury intrusion porosimetry (MIP) method (see Fig.1a) and by the gas adsorption method (see Fig. 1b). The results show that the connected porosity is 13.4% and the pore size covers a wide range from 1 nm to several hundred nanometres.

The pore structure of COx claystone which dominates the flow and transport properties has been characterised by direct imaging methods, i.e.transmission electron microscopy(TEM),focused ion beam/scanning electron microscopy (FIB/SEM) (Song et al., 2015,2016, 2017) and indirect methods, i.e. nuclear magnetic resonance (NMR), MIP or N2adsorption (Yang et al., 2010). Direct imaging provides all the necessary pore space information(pore size distribution,pore connectivity,pore shape and tortuosity,etc.),but pore sizes significantly depend on the resolution of the imaging techniques. In addition, the accuracy of the imaging methods depends on the analysed sample size and the algorithms used to segment pore space as different algorithms may lead to large difference in the porosity and pore size distribution(Song et al.,2015).Although the MIP has the disadvantages of “ink bottle effect”, it is still appealing as it covers a much wider pore size range and can analyse a larger sample size compared to other imaging techniques based on simpler physicochemical principles, in a much faster operation fashion(Xiong et al.,2016).The pore size measured by N2adsorption is in the range of 2-100 nm while the pore size measured by MIP is in the range of 7-1000 μm.The pore size range of COx claystone covers several orders of magnitude which cannot be captured by one single method. As the MIP and N2adsorption can cover the whole pore size range of COx claystone (Song et al.,2015) and only connected pores contribute to the transport properties, it is reasonable to use MIP and N2adsorption data for analysis of transport properties.Most importantly,to avoid the sample diversity effects, in this work, the samples used for effective gas permeability tests are cut off and prepared for MIP experiment to measure the pore size distribution (Yang et al., 2010).

To understand the gas transport properties of COx claystone and evaluate the safety of the radioactive nuclear waste repository,the French National Waste Management Agency(Andra)has launched a gas permeability measurement benchmark and a series of experimental tests have been carried out in several laboratories(Davy et al.,2012).The study shows that the water permeability of the COx claystone varies between 10-20m2and 10-22m2(Homand et al., 2004). In consideration of the water sensibility of the material, the gas is often used as fluid medium for permeability measurement (Davy et al., 2007) and it can shorten the test time and characterise the permeability of the partially saturated COx claystone. The results obtained in several laboratories (Homand et al.,2004; Davy et al., 2007; Boulin, 2008; Yang et al., 2010; M'Jahad,2012) show that the permeability (k) of the material increases with decreasing saturation(Sr),and it varies between 10-16m2and 10-24m2. Although the measured data are scattered, Yang et al.(2010) and M'Jahad (2012) found a quasi-linear relationship between log10k and Sr. The different permeabilities are related to several factors, e.g. initial damages and various pore size distributions.In this study,we chose a typical pore size distribution which is similar in several samples (Yang et al., 2010).

3. Numerical method

3.1. Pore network construction

Fig.1. Experimental pore size distribution of the COx claystone:(a)Pore size distribution measured by MIP with porosity of 10.8%;and(b)Pore sizes smaller than 6 nm measured by N2 adsorption with porosity of 2.6% (Yang et al., 2010).

A cellular assembly based on truncated octahedron is used to represent the COx claystone,which is in line with the experimental characterisation. The model based on truncated octahedrons has been developed to represent the neighbourhood of different measureable features,i.e.solid particles(Jivkov and Yates,2012)or pores (Jivkov and Xiong, 2014; Xiong et al., 2014). The mechanical deformation and crack initiation/propagation (Jivkov et al., 2012)and reactive transport (Jivkov and Xiong, 2014; Xiong et al., 2014)can be simulated through the corresponding developed models.The particle/pore sizes can be mapped to different regions and directions to achieve the anisotropy and heterogeneity of the materials.

Considering six square faces of the truncated octahedron perpendicular to three coordinate axes, i.e. x-direction (1, 0, 0), ydirection(0,1,0),and z-direction(0,0,1)(m),three different length parameters, S1(m), S2(m), and S3(m), are used to represent the lengths between the square faces in the three directions, respectively.All other parameters related to the length are calculated and represented based on above three length parameters.For instance,the volume of each cell can be calculated by Vc= S1S2S3/2 (m3). In an assembly of Nccells,the relationship between pore volume and total volume can be expressed by

where φ is the measured porosity,Ntotalis the total number of pores in the model, riis the pore radius, Npis the total number of pores,and liis the pore length which can be obtained from the length scales. The calculation of the three length parameters from Eq. (1)depends on the ratio values used to represent texture.S1= S2= S3= S is in a non-textured medium.

In this work,a non-textured medium is considered which does not take into account the anisotropy of COx, and the volume percentage of pores and pore size distribution of the COx claystone measured by MIP and N2sorption were used to generate the network, as shown in Fig.1. The pore sizes ranging from 6 nm to 100 nm in the model are obtained from MIP with porosity of 10.8%,while the pores with radii in the range of 2 nm-6 nm are from N2adsorption data.The pore sizes analysed by MIP and N2sorption are based on the assumption of circular pore shapes and only connected pores can be measured. The Barrett-Joiner-Halenda (BJH)method(Barrett et al.,1951) is used to interpret the N2adsorption results based on the assumption that the pores are cylindrical.The MIP tests are interpreted by inversely proportional relationship between intruded pore sizes which are assimilated to cylindrical capillaries and the applied pressure governed by the Washburn-Laplace equation (Xiong et al., 2016). The measured pore size distribution (Fig. 1a) was assigned to each bond connecting the neighbouring cell centres and then S can be determined from Eq. (1). Specifically, the pores measured by MIP are distributed to each available bond (see Fig. 2a) in accordance with the MIP experimental data.Hereafter,we name these pores as larger-pores.All these pores should be connected to avoid isolated pores or clusters. For available bonds, no pores have been assigned previously. Secondly, pores measured by N2adsorption but not measured by MIP are randomly assigned to bonds. Hereafter, we call these pores as smaller-pores.The process terminates when the volume of all allocated pores,from larger-to smaller-pores,is equal to the experimentally measured porosity. It should be noted that the number of smaller-pores assigned to a bond is not limited in order to achieve the prescribed porosity,as illustrated in Fig.2c.As the pores are measured by MIP, all pores should be connected, i.e.no pores are isolated. The constructed pore network is shown in Fig. 2.Theoretically, the water intrudes the smaller pores first to achieve saturation. Therefore, the pores in the network available for gas flow under certain degree of saturation can be obtained by removing smaller pores occupied by the liquid. The smaller pores occupied by the liquid can be calculated by

Fig. 2. (a) Pore network pores are assigned to bonds (purple); (b) Pore network with 90%saturation;and(c)Schematic of larger-pores and smaller-pores assigned to bonds.

where N is the number of pores with radii smaller than a fixed value rfixed. After trying different values of rfixed, different values of saturation can be achieved.

3.2. Water flow equation in pores

For water flowing through saturated COx, the flow equation through a pore can be described by the Hagen-Poiseuille equation(Xiong et al., 2015):

where Aijis the pore cross-section equal to Aij= πr2ij(m2), with pore rijconnecting nodes i and j;qij(m3/s)is the volume flow rate;m is a dimensionless coefficient with the value of 0.5, 0.6, and 0.5623,respectively,for a circular,an equilateral and a square tube(Patzek and Silin,2001).In this work,0.5 is used for m.μ(Pa s)is the water dynamic viscosity which is usually 8.9 × 10-4Pa s at room temperature of 25°C;piand pj(Pa)are the pressures at pores i and j,respectively. Eq. (3) is assumed to be appropriate for describing water flow in pores (Bear, 2013) and is valid for laminar flow in a wide range of Reynolds numbers. For incompressible, steady state flow, the sum of discharges of pores connected to a node must be zero:

where ziis the number of pores connected to node i. Then the average permeability kw(m2) can be determined as

where Q(m3/s)is the total water discharge through the network,L(m) is the network length in the flow direction, A (m2) is the network cross-section, Pinis the water pressure on the inlet boundary, and Poutis the water pressure on the outlet boundary.

3.3. Gas flow equation in pores

The gas flow through micro- and nano-scale channels can be divided into different flow regimes (see Fig. 3) according to the value of the Knudsen number Kn, which is the ratio of molecular mean free path to the characteristic length of porous medium(Guo et al., 2015):

where λ denotes the mean free path of gas molecules,which can be written as

where μ is the viscosity of gas(Pa s),p is the absolute gas pressure(Pa), R = 8.314 J/(mol K) is the universal gas constant, T is the absolute temperature (K), and M is the molecular mass of gas (kg/mol), and M = 39.948 × 10-3is used in this study.

As Kndecreases, the flow regime transfers from free molecule model to continuum model (shown in Fig. 3). In this work, the Argon at the temperature of 293 K and the pressure of 3 MPa is considered which corresponds to the value of λ ≈2 nm. For the pore sizes in the range of 1 nm-100 nm as shown in Fig.1,Knranges from 10-3to 100. As Knis in the range of slip flow regime and transition flow regime,only the slip flow and transition flow model are considered in this work.Different models are illustrated below.

Various equations have been proposed to calculate the apparent permeability in tight porous media (e.g. Klinkenberg, 1941;Karniadakis et al., 2006; Javadpour et al., 2007; Civan, 2010;Sakhaee-Pour and Bryant, 2012; Yang et al., 2017; Song et al.,2019). In this work, these different models are used to predict the apparent permeability of the COx claystone under different saturations and then are compared with experimental data to show the accuracy of the models.

(1) Javadpour model

Javadpour(2009)derived an apparent permeability equation in a single nanopore. This equation is a combination of Knudsen diffusion and viscous flow where the mass flow in a circular pore is written as

Fig. 3. Fluid flow regimes defined by ranges of Kn and fluid models (Guo et al., 2015).

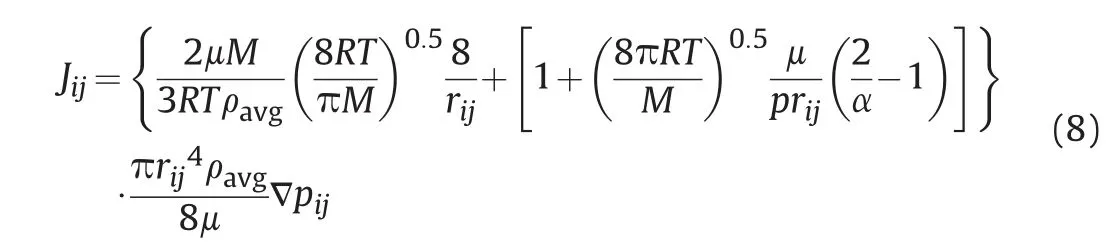
where ρavgis the average density (kg/m3), and α is the tangential momentum accommodation coefficient which can be determined by experimental measurements.The value of α varies theoretically from 0 to 1, depending on wall surface smoothness, gas type,temperature and pressure(Javadpour,2009).In this work,α=1 is used.

(2) DGM model

The DGM is a linear combination of the gas transport mechanisms (viscous flow, Knudsen diffusion and ordinary diffusion) to predict the overall flow rate(Sakhaee-Pour and Bryant, 2012):

(3) Civan model

Civan model is expressed by

where b is the slip coefficient and equal to-1 for the slip flow.The rarefaction coefficient β(Kn) given by Civan (2010) is

The rarefaction coefficient β(Kn) given by Karniadakis et al.(2006) is

(4) Klinkenberg model

Klinkenberg model is written as

where β is equal to 4 (Klinkenberg,1941).

3.4. Gas flow with fractures

When the minimum principal stress and the tensile strength of COx claystone are smaller than the gas pressure, the fractures develop (Valko and Economides, 1995). The gas flow in such a fracture can be considered as a single-phase flow process. The gas flow in fractures can be described by cubic laws (Zaouter et al.,2018):

where h is the aperture of the fracture,ξ is a factor that depends on the tangential-momentum accommodation coefficient (TMAC),and ξ = (2-α)/α is the second term in the parentheses reflecting the correction for the slip flow.

The network of pores in the range of 1-100 nm,which is defined as NetSmall, is superimposed on the network with fractures(10 μm)defined as NetLarge.New nodes will be added in the large network when the bonds in the NetSmall intersect with the fractures in the NetLarge. Then bonds of NetSmall which intersect fractures of NetLarge are replaced by bonds between the new added nodes and the original NetSmall nodes.Thus a new network configuration is constructed, as shown in Fig. 4.

4. Results and discussions

4.1. Simulation setup and network properties

The input information for the construction of the model is the pore size distribution obtained from experiments (Fig. 1). The boundary conditions are: for fluid transport in saturated COx, the constant pressures Pinand Poutare prescribed on the inlet and outlet boundaries, such as X0and X1, respectively. The remaining boundaries are isolated; for the gas permeability simulation, the gas pressure difference is imposed on the opposite boundaries.For example, a constant pressure P0is applied to the boundary X0where the x-coordinate of all nodes in this face is equal to zero and a constant pressure P1is ascribed to the boundary X1where the xcoordinate of all nodes in this face is equal to 20S1.In the meantime,all other boundaries parallel to the transport direction are isolated.The flowchart of the gas permeability calculation is shown in Fig.5.

4.2. Model validation and comparison

Fig. 4. Schematic diagram before and after the combination of pore network (NetSmall) and fracture network (NetLarge).

The developed model is first validated by comparing the predicted water permeability and experimental measured value.Then different models used to predict gas permeability are discussed and compared with experimental data under various saturations. The predicted water permeability in water saturated network is 3.1×10-21m2which agrees with the measured value in the range of 1×10-20to 1×10-22m2(Homand et al.,2004;Harrington et al.,2012;M'Jahad et al.,2017).The predicted apparent permeability of argon under different degrees of saturation calculated by different equations is compared with the experimental data (Boulin, 2008;Andra, 2009; Yang et al., 2010; M'Jahad, 2012), as illustrated in Fig. 6. Generally, the predicted apparent permeability is in agreement with the experimental data. The order of predicted values is Javadpour ＞DGM ＞Civan ＞Klinkenberg. In addition, when the degree of saturation increases,larger pores in the model are left for the gas flow and thus the viscous flow has a greater impact on gas transport. The difference between the predicted apparent permeabilities decreases as the degree of saturation increases, as the pores with radii smaller than 1 nm cannot be measured directly by the experimental methods used in this work. The effects of pores smaller than 1 nm are not taken into account in the gas transport prediction which has a significant role in the smaller degree of saturation. This is consistent with the theoretical and other numerical predictions (Yao et al., 2013). It is noted that the permeability measured by Boulin (2008) is the intrinsic permeability of the COx claystone sample and is smaller than the apparent permeability measured by Yang et al. (2010). The reason why the results predicted by Javadpour's model are larger than those predicted by DGM is that the Javadpour's model (Javadpour, 2009)tried to combine diffusion and advection to describe the gas transport in nanopores. It used Brown's equation to describe the gas flow in pipes at low pressures (Brown et al., 1946) and the advection flow term. Brown's model is actually identical to DGM which is rigorously derived from basic physics (Zhdanov et al.,1962; Mason et al., 1967). These models actually have already taken into account the diffusion in the equation. Thus Javadpour double counts the Knudsen diffusion term in his equation(Eq.(8)in this work). The difference between the experimental data and predicted results is due to following facts:

Fig. 5. Calculation flowchart from input to output for the steps of simulations.

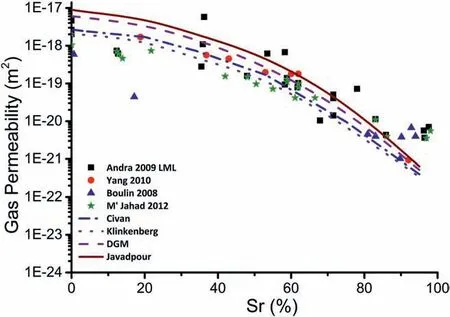
Fig. 6. Experimental and predicted gas permeabilities of the COx claystone.

(1) The characterised pore space information is different from the realistic pore space. Although the pore network constructed from MIP and N2adsorption data can reasonably predict the gas flow as all relevant details are identified and included(Xiong et al., 2016), they have some disadvantages like ink bottle effects for MIP method. More specific microstructure information needs to be measured by different direct imaging techniques and indirect methods across different length scales to represent more realistic the porous medium in the future.

(2) All the gas transport models (Javadpour, DGM, Civan and Klinkenberg) assume the pores as the circular cross-section shape although they are based on the combined fundamental physics mechanisms of Knudsen diffusion and viscous flow in tight porous media.The effects of different pore shape are other aspects in our future work.In addition,all proposed transport equations for the gas transport in tight porous media are summarised and compared in the first time to predict the gas apparent permeability in the different degrees of saturation. The predicted results by different models are not identical; nevertheless, this gives a general concept of the difference between different gas transport models and how to choose appropriate model in future application.Further study of transport equations considering the combined transport mechanisms in tight porous media should be conducted.

(3) The effects of structural anisotropy,i.e.the gas permeability may be different in perpendicular and parallel to the bedding planes of the COx claystone stratum,are not considered in this work.

(4) The difference between the predicted gas permeability and measured values is greater at smaller water saturations.One explanation for the predicted result larger than the experimental value is that the argon adsorption on the clay mineral surfaces is not taken into account in the model.

(5) The reason that the predicted results are smaller than experimental data at larger water saturations is that the clay particles are separated into smaller particles as the degree of saturation increases.This will lead to the pore decrease and closure due to minerals swelling (Saiyouri et al., 2000). This is not considered in the current models either.

4.3. Gas flow with fractures

After validation of the small-scale model, the small-scale network is then superimposed on a large-scale network to analyse the effects of fractures. The three-dimensional (3D) geometry illustrated in Fig.7 shows a block of COx claystone with 1 cm length on each side.The added fractures with a thickness of 10 μm are far more permeable to gas and fluids than the matrix block, and are much smaller than the block dimensions. The single phase of gas flow is considered to analyse the effects of fractures. The pressure contours in COx claystone with different fracture structures are shown in Fig.7 when the gas pressure difference is imposed on zdirection while the other boundaries are impermeable. It can be observed that larger pressure drops in the vicinity of crack tips and less pressure drops along the crack length.

The permeabilities of COx claystone with various fracture structures in x-, y- and z-direction are calculated by imposing pressure difference on opposite boundaries in x-,y-and z-direction while other boundaries are impermeable.The Klinenberg equation is used to simulate the gas flow in nano-pores as it fits best with the measured gas permeability under different saturations. Eq. (14) is used to predict the gas flow through fractures.The predicted results are demonstrated in Table 1.It is evident that the permeabilities in the x- and y-direction are independent of the fracture positions.However, the permeability in z-direction relies on the fracture positions to some extent.For the cases with one fracture parallel to z-direction and two fractures perpendicular to z-direction in yzplane, the permeability in z-direction decreases as the distance between the two fractures parallel to y-coordinate axis decreases.For the cases with one fracture parallel to z-direction and one perpendicular to z-direction, the permeability in z-direction is the largest when the fracture perpendicular to z-direction intersects with the middle of the fracture parallel to z-direction.Furthermore,the permeability in z-direction is the same when the fracture parallel to y-direction intersects with the end of the fracture parallel to z-direction. The permeability in z-direction with and without fracture parallel to y-direction intersecting the middle of fracture parallel to z-direction is the same.In addition,all the permeability values with fractures are larger than the values without fractures.

When fractures are coupled in the model, the fractures are the dominant channel for the gas flow, and the gas permeability is dependent on the fracture positions when all other conditions are unchanged. The gas permeability in z-direction decreases as the distance between the fractures in y-direction decreases. It is because more gas flow is diverted to y-direction as the distance between the fractures in y-direction decreases.More details on the curvature and toughness of fractures need to be studied in the future.In addition,the model with fractures is of centimetre scale.Only pores measured by N2sorption and MIP are considered while pores that are not in the measured range will not be considered.Multi-scale measurement of the pore side distribution is required in the future to fully represent the pore space characteristics. The propagation and new initiation of micro-fissures which may be caused by dilatancy are not discussed in this work.

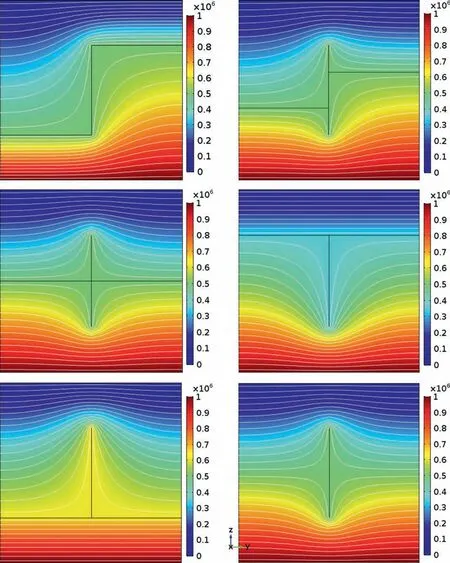
Fig. 7. Pressure contours in COx with different fracture structures (black lines represent fractures) (unit in Pa).

Table 1 Permeability of COx claystone with various fractures structures in different directions when applying pressure difference in z-direction while other boundaries are impermeable.

5. Concluding remarks

In this study, a reliable multi-scale pore network model with fractures is developed based on the fundamental pore space characterisations and physics. The predicted water and gas permeabilities agree well with the experimental data.

The advantages of the developed model are as follows:

(1) The model can reflect the realistic pore space characterisation as it is constructed from the information of pore size distribution,pore morphology and pore connectivity measured by experiments.The anisotropy is not discussed in this work but can be achieved by changing the ratios between S1,S2and S3.An example of this can be found in Xiong et al.(2015).

(2) The water and gas transport is predicted by fundamental physical equations. No fitted or calibrated parameters are used in the model.

(3) The developed model not only covers the gas transport mechanism in nanopore scale regions(i.e.the discontinuous flow in most of the pores),but also in the microscale regions(i.e. the continuous flow in the fractures) by reflecting the pore space information at both levels. Current modelling methods usually use the matrix obeying Darcy's law when coupling with fractures. This, unfortunately, is not in correspondence with the reality.

(4) The developed model is reliable and could be applied to other fields such as capture and storage with a focus on capillary trapping as a mechanism to store carbon dioxide in geological porous media.

The disadvantages of the developed model are that it cannot simulate the effects of stress states,i.e.confining stress and axialstress.These will change the pore size distribution and liquid and transport properties of COx claystone.This will be an interestof our future work.Other improvements of this model in the future will (1) take into account the surface chemistry of different pores,e.g.hydrophilic clays and hydrophobic organic pores;(2)reflect the real fracture system in the model and compare the results with experimental data; (3)include nanopores not covered by N2adsorption and MIP tests, e.g.pores in the range of 0-2 nm. In this case, experiments like CO2adsorption are required to measure the pore size distribution first.

Declaration of Competing Interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgments

The authors would like to thank the anonymous reviewers for their comments and suggestions. We gratefully acknowledge the support of the National Natural Science Foundation of China(Grant Nos.41572290,51879260 and 51879258),and CAS Interdisciplinary Innovation Team (JCTD-2018-17).

List of notations

VcVolume of each cell

NcTotal number of cells

S1Length parameter in x-direction

S2Length parameter in y-direction

S3Length parameter in z-direction

φ Measured porosity

rijPore radius

AjjPore cross-section

NpTotal number of pores

liPore length

SrDegree of saturation

NtotalTotal number of pores in the model

N Number of pores with radii smaller than a fixed value rfixed

λ Mean free path of gas molecules

μ Viscosity of gas (Pa s)

p Absolute gas pressure(Pa)

R Universal gas constant

T Absolute temperature(K)

M Molecular mass of gas (kg/mol)

ρavgAverage density (kg/m3)

α Tangential momentum accommodation coeffciient

b Slip coefficient

β(Kn) Rarefaction coefficient

h Aperture of the fracture

ξ A factor that depends on the tangential-momentum accommodation coeffciient (TMAC)

AijPore cross-section equal to Aij=(m2)

qijVolume water flow rate

m A dimensionless coefficient with the value of 0.5,0.6,and 0.5623, respectively, for a circular, an equilateral and a square tube

μwWater dynamic viscosity which is usually 8.9×10-4Pa s at room temperature of 25°C

pi, pjPressures at pores i and j, respectively(Pa)kwAverage water permeability

Q Total water discharge through the network L Network length in the flow direction PinWater pressure on the inlet boundary PoutWater pressure on the outlet boundary KnKnudsen number