《机械原理》中引入系统论的教学设计的探讨

范 娜，王 群，陆知遥

（电子科技大学，四川 成都 611731）

一、《机械原理》的重要性及其存在的不足

《机械原理》是研究机械共性问题的专业核心基础课，重在引导学生探究机械系统的本质，这对未来开发新的机械系统至关重要。然而，众多高校使用的现有教材对机构确定运动的条件并未做本质的阐述，也未给出相应的数学解释。

二、《机械原理》与系统论之间的关系

《机械原理》是对机械系统的分析、设计以及控制。它本质上是将系统论中的内容具体应用到了机械学科之中。在现代系统论之中，状态空间向量法是一种重要的研究手段，它是一种基于解答空间的问题表示和求解方法，该方法可以比较全面地反映系统各部分之间的相互联系，解释系统运动的规律和机制。

三、用系统论的思想建立机构运动模型

在系统论中，系统的状态向量指的是确定系统状态的个数最少的一组变量，在《机械原理》中，我们关心的是构件的空间位置，所以这里的状态向量指的是确定构件位置的最少向量组，这组独立参数组的个数就是某一机构的自由度。运动元素的状态与很多的参数有相互联系，以一个杆件举例，其运动状态与其中点的位置，其与三个坐标轴的夹角，其某一个端点的位置，等等都有关。而根据状态向量的定义，我们可以根据系统的状态向量来确定所有与系统状态有关的变量。下面我们用公式来表达这种确定关系，假设与某一运动元素的状态S与S1，S2，S3，S4…有关，其中的S1，S2，S3为确定这一运动元素状态的状态向量。用数学公式表示就是：

其中

在上式中，f为通过S1，S2，S3来表征S的函数关系式，A为S1，S2，S3来求取S的矩阵。

以一常见构件为例，如图1杆件AB。

图1 杆件AB

将平面上的杆件AB视为一个基本运动元素，SAB为杆件AB的状态，具体而言也就是杆件AB在平面中的位置。根据先修知识与“杆是刚性的”假设，我们可以根据点A在平面上的位置（可取其坐标系中的横纵坐标，2个参变量，设为XA、YA），点B在平面坐标系中的横坐标（1个参变量，设为XB），一共3个参变量来完全确定杆件的位置。

举例来说，杆上点的横坐标我们可以通过XA，YA，XB来表示：

所以，确定该杆件位置所需的独立参变量的数目为3，也就是这个杆的自由度为3。

系统的结构方程指的是反映系统结构关系的一组方程组，对于系统的完整的描述称为系统的结构空间表达式，建立系统的结构空间表达式要根据系统的物理机理建立相应的方程组，并选择有关的物理量作为状态向量，从而得到系统的结构空间表达式，并最终完成对系统的分析工作。

基于以上有关系统论的介绍，接下来对机械原理中的机构和概念进行解析。

以四杆机构为例，如图2的四杆机构。

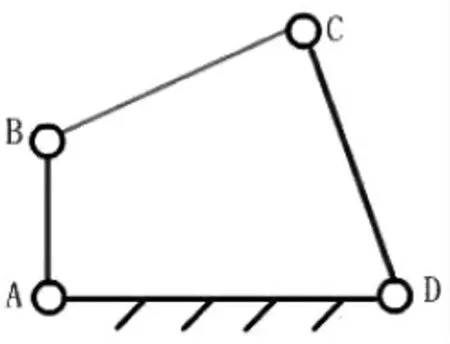
图2 四杆机构ABCD

该机构中的基本运动元素为3个固定杆件。这三个基本运动元素的状态我们用SAB，SBC，SCD来表示，根据上面的公式1.2，我们可以得到如下方程组：

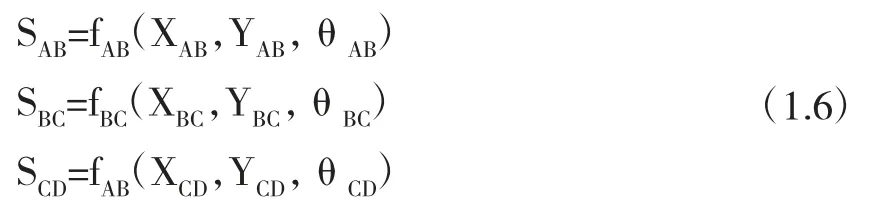
上式中的XAB，XBC，XCD表示各杆件中点的横坐标，YAB，YBC，YCD表示各杆件点的纵坐标，θAB，θBC，θCD表示各杆件与x轴的夹角。

下面我们要根据系统的物理机理建立结构空间表达式，也就是各个约束的物理意义映射到数学域上的情况。以B点的转动副为例，转动副的要求是AB杆上的上端与BC杆上的左端处于同一位置，即

显然XAB上，YAB上是AB杆运动状态的一部分，即

同理

根据式1.6式1.9有

合并式（1.9），（1.10）可以得到

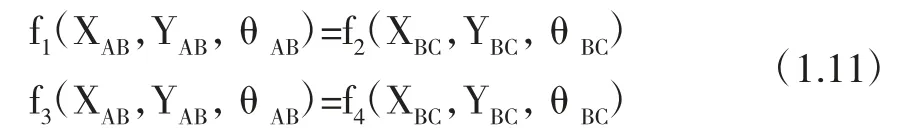
等价于

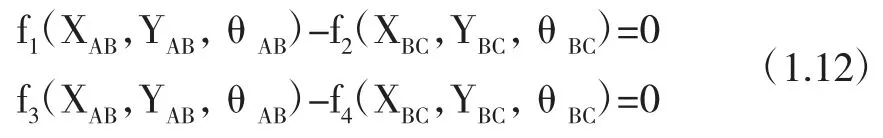
等价于

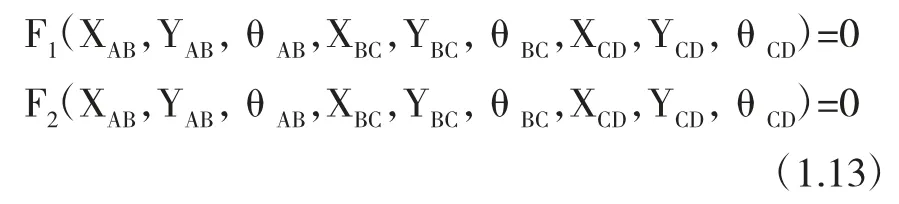
这样我们就得到了两个结构方程，再将其他三个约束写为同样的形式，有：

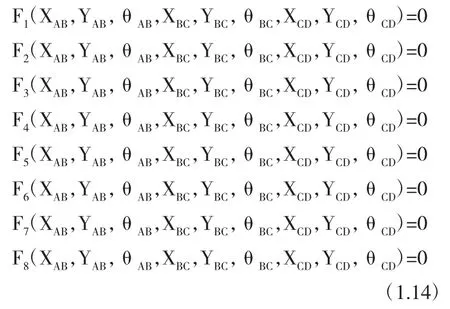
这样即得到了8个结构方程，但由于共有9个参变量，根据线性代数和系统论，要完全确定每一个未知参数的值，我们就要引入与其相对应的信息，每一个方程描述的是一个信息。上述情况中方程数小于参变量数，也就是说引入的信息量小于未知的信息量，系数矩阵的秩与增广矩阵的秩相等且小于未知量数n，方程组存在无穷多解，无法得到参变量的确定值。这也就说明该四杆机构的状态S并不是确定的，而若使其得到一个确定值，需要再引入一个信息，这就使得方程组系数矩阵的秩与增广矩阵的秩相等且等于未知量数n，方程组有唯一解，也就是确定的机构状态。该方程的引入即为原动件的外部输入，比如将杆AB视为原动件，在其运动的某一状态杆AB与x轴垂直，即α=90°。α=90°作为新引入的方程，使整个四杆机构的状态实现确定。而若使机构的原动件按照给定的运动规律运动时，如α为随时间改变的量（比如α=3t°），机构的其他构件也会按照一定的规律运动，整个机构的运动便确定下来。