自动化分拣仓库中多AGV调度与路径规划算法
余娜娜,李铁克+,王柏琳,袁帅鹏
(1.北京科技大学 东凌经济管理学院,北京 100083; 2.钢铁生产制造执行系统技术教育部工程研究中心,北京 100083)
0 引言
随着电子商务的飞速发展,人们对高效快速的物流需求越来越迫切,如亚马逊、京东和顺丰等电子商务企业或物流公司纷纷建立了自动化分拣仓库。自动化分拣仓库能够对包装好的包裹,以其收货地址为分类标准,使用自动导引小车(Automated Guided Vehicle, AGV)实现包裹的自动分拣。当包裹数量较多时,每个AGV需要搬运多个包裹,且有多个AGV同时搬运,因此,需要为每个包裹指定搬运的AGV并确定其在AGV上的搬运顺序,此即多AGV的调度问题;此外,需要给每个AGV的每次搬运任务规划搬运路径,保证多个AGV在搬运过程中不发生冲突,并使得最大搬运完成时间最短,此即多AGV的路径规划问题[1]。在自动化分拣仓库中,多AGV调度与路径规划是关系到分拣作业高效运行的关键与核心问题,单独考虑调度或搬运路径都只能达到局部优化的效果,而将调度问题与路径规划综合优化则能更好地提高仓库的分拣效率。
目前,有关AGV调度与路径规划问题的研究多是聚焦于其中的一个问题,鲜有文献对调度和路径规划问题进行综合优化,下面分别从AGV调度问题和AGV路径规划两方面进行综述。
对于AGV调度问题,目前的研究主要分为单AGV调度和多AGV调度,对于单AGV调度问题,文献[2]建立了一个线性规划模型,并研究了各个因素对目标函数的影响;对于多AGV调度问题,文献[3]对五种动态调度规则进行了对比;文献[4-5]分别提出了基于遗传算法和粒子群算法的混合算法以及改进Memetic算法。但以上研究均假设AGV在执行每次搬运任务时的搬运路径提前确定且搬运过程中不会发生冲突。文献[6]提出一种改进花授粉算法对AGV与机器集成的车间调度问题进行了求解,但未考虑多AGV之间的冲突和死锁问题;文献[7]同时考虑AGV无冲突的路径选择和车间调度问题,提出一种两阶段蚁群算法,但AGV只能沿既定路径行走,增加了AGV之间路径冲突的可能性,降低了系统柔性。自动化分拣仓库中的AGV体型较小,单个AGV的分拣能力有限,且包裹数量较多,需要多个AGV同时分拣,因而AGV之间发生冲突的概率较大,多AGV之间的冲突问题不可忽略。因此,在调度优化的同时必须要考虑路径规划,为AGV设计合理的调度方案,并为其规划出搬运过程中无冲突的作业路径。
对于AGV路径规划问题,求解算法主要有遗传算法[8]、蚁群算法[9]、Dijkstra算法[9]和A*算法[10]等,但是这些算法仅能解决单个AGV的最短路径规划问题。当多个AGV同时工作时,如何有效地避免AGV之间的冲突显得尤为重要。肖海宁等[11]定义了单环路死锁和多环路死锁的临界状态,并设计了对应的死锁控制策略。张丹露等[12]利用改进的A*算法预约表和动态加权地图,实现了多AGV的动态协同路径规划。Malopolski[13]针对具有方形拓扑结构和多AGV的运输系统,基于保留链提出了一种防止冲突和死锁的方法。以上文献虽然对多AGV的冲突和死锁问题给出了解决方法,但均未对搬运任务(包裹)和AGV之间的合理分配进行研究。
由上述文献可见,多AGV调度研究多是假定AGV的搬运路径已经确定,且AGV间不会发生冲突,而多AGV路径规划的研究多是假定AGV的搬运调度已经确定,鲜有文献对多AGV调度和路径规划进行综合优化。本文针对自动化分拣仓库的多AGV环境,研究调度和路径规划的综合优化。首先针对多AGV路径规划问题,提出了AGV优先级并设计了无路径冲突的多AGV路径规划算法,进而综合考虑多AGV调度和路径规划,设计了一种改进差分进化算法,其个体对应多AGV调度方案,每个个体采用提出的路径规划算法来确定搬运路径。为验证算法性能并观察关键问题参数的影响,在本文最后设计了数据实验进行实验分析。
1 问题描述
本文借鉴文献[12]中的智能仓库模型,提出一类典型的自动化分拣仓库模型,并采用栅格图进行表示,如图1所示。图1主要包括以下部分:①分拣台:位于地图最左侧,用于放置已经打包完成的包裹;②道路:图1中的白色栅格,用于AGV的行走;③包裹投递区:根据包裹的收货地址,在地图上均匀地分割出多个投递区,每个投递区有一个垂直向下的缓存区,当缓存区的包裹量达到上限时将其运出仓库装车;④AGV:以一定的速度在仓库中行走并搬运包裹;⑤包裹目的地:包裹投递区与包裹目的地相对应,若包裹投递区为1,则AGV需行驶至栅格1进行投递;⑥停靠区:用于空闲AGV的停靠,所有AGV从停靠区出发,当其搬运序列中的包裹全部搬运完成后返回停靠区。
为了在最大程度上减少冲突和死锁,降低交通管理难度,本文采用单向导引路径网络(Unidirectional Guidepath Network, UGN)[11],即AGV在每条路径上只允许单方向行驶,且相邻两条路径的方向相反[12]。此外,由于自动化分拣仓库多采用小型AGV,假设每个AGV一次只能搬运一个包裹,每个包裹只能被一个AGV搬运,且所有的包裹都必须被搬运。

以模型构建的现实性和易处理性为原则,不失一般性,提出如下假设:
(1)AGV可横向或纵向跨越栅格,不允许沿对角线方向跨越栅格。
(2)不考虑AGV的装载和卸载时间,即AGV的装载和卸载时间均为0。
(3)所有包裹在零时刻到达,所有AGV在零时刻可用。
(4)AGV运行过程中保持匀速。
(5)不考虑包裹到达投递区之后的出库过程。
为便于描述,定义以下符号:
(1)下标与参数i表示包裹编号,I表示包裹编号集合,i∈I={1,2,…,n};j表示AGV编号,J表示AGV编号集合,j∈J={1,2,…,m};AGVj表示编号为j的AGV;o表示栅格编号;l表示栅格边长;v表示AGV的行走速度;tw表示AGV单次停车等待的时间,即当一个AGV需要避让另外一个AGV时,所需要在原地停车等待的单位时间,若一次需要避让多个AGV,则记为多个停车等待时间。
(2)决策变量πj表示AGVj的搬运包裹序列,πj(r)为πj的第r个任务(即包裹),|πj|=sj;{π1,π2,…,πm}:所有AGV的搬运包裹序列,对应一个调度方案;zorjt表示0-1变量,若AGVj在t时刻将包裹πj(r)搬运至栅格o则为1,否则为0;nrjw表示AGVj搬运包裹πj(r)过程中的停车等待次数。
(3)决策变量的衍生变量trj表示AGVj搬运包裹πj(r)所需的时间;Tj表示AGVj的搬运完成时间;Tmax表示最大搬运完成时间。trj、Tj和Tmax计算方法如下:
(1)
基于以上符号,最小化最大搬运完成时间目标可表示为:
(2)
对于本文问题,若将n个包裹视为n个工件,m个AGV视为m个并行机,则在搬运路径确定的情况下,多AGV调度问题等价于无关并行机调度问题(Unrelated Parallel Machine Scheduling Problem, UPMSP),其求解方法有精确算法[14]和智能算法,由于UPMSP是NP-难的,精确算法对大规模问题的求解非常困难,因此求解方法多采用智能算法,如遗传算法、禁忌搜索及其混合算法[15]、自适应分布估计算法[16]等。差分进化算法(Differential Evolution,DE)[17]是一种群体智能算法,其基于差分的简单变异操作和一对一的竞争生存策略降低了遗传操作的复杂性,具有较强的全局收敛能力和鲁棒性。针对多AGV调度问题,本文设计了一种改进差分进化算法。
针对多AGV的调度与路径规划联合决策,本文基于以下思路展开研究:首先探讨在AGV搬运包裹序列确定的情况下,如何规划无冲突的AGV搬运路径;进而在路径规划方法的基础上,设计改进差分进化算法实现多AGV调度与路径规划的综合优化。
2 多AGV路径规划算法
针对AGV搬运包裹序列{π1,π2,…,πm}确定的情况,提出了一种多AGV路径规划算法。
A*算法作为最佳优先的启发式算法,具有搜索空间小、计算速度快等优点,被广泛应用于AGV的静态路径规划中[10]。多AGV路径规划算法首先在不考虑冲突的情况下运用A*算法为每个AGV的每次搬运任务规划路径。当有多个AGV同时工作时,由A*算法规划的路径在AGV间会产生冲突。本章算法进而计算AGV经过各个路径栅格的时间窗,判断是否存在冲突,并提出一种确定冲突AGV优先级的方法,对优先级较低的AGV的时间窗进行动态更新,以解决多AGV间的冲突。
多AGV间的冲突有节点冲突、相向冲突和追击冲突[11]。由于本文为UGN环境,并假设AGV匀速行驶,可避免相向冲突和追击冲突的发生,因此,本章重点解决AGV间的节点冲突。用Ojr表示AGVj搬运包裹πj(r)所经过的栅格序列(搬运路径),用inTjr和outTjr分别表示AGVj进入和离开栅格序列Ojr的时间序列。根据πj中每个包裹的搬运路径可将AGVj的总搬运路径Oj表示为:Oj={Oj1,Oj2,…,Ojsj},AGVj进入和离开Oj的时间序列可分别表示为:inTj={inTj1,inTj2,…,inTjsj},outTj={outTj1,outTj2,…,outTjsj}。设oji为AGVj搬运路径中的一个栅格,oki为AGVk搬运路径中的一个栅格,(j,k∈J)∧(j≠k),intji为AGVj进入栅格oji的时间,intki为AGVk进入栅格oki的时间,则AGV间的节点冲突识别方法如下:
(1)节点冲突识别规则 若oji=oki且intji=intki,则AGVj和AGVk在intji(intki)时刻发生节点冲突。
对于发生节点冲突的AGV,按照以下规则定义优先级,以此确定进入冲突栅格的优先顺序:
规则1将Jconflict中的AGV按搬运完成时间递减排序,为搬运完成时间大的AGV赋予高优先级,其中Jconflict表示发生节点冲突的AGV集合。
规则2若不满足规则1,即多个AGV具有相同的搬运完成时间,则计算Jconflict中各AGV与其他AGV发生的冲突次数之和,为冲突次数少的AGV赋予高优先级。
规则3若不满足规则1和规则2,即多个AGV的搬运完成时间和冲突次数之和均相等,则计算Jconflict中各AGV与其他AGV路径中相同栅格的个数,为相同栅格个数多的AGV赋予高优先级。
规则4若存在多个AGV均不满足以上3条规则,则随机决定AGV的优先级。
规则1保证冲突的解决可以不增加目标函数值Tmax;规则2使得冲突次数少的AGV可以顺利行驶,提升搬运效率;规则3使得相同栅格个数多的AGV优先通过,降低了因停车等待而使相同节点变成冲突节点的概率,减少潜在冲突次数。根据以上规则,让Jconflict优先级最高的AGV进入冲突栅格,其他AGV停车等待,待当前AGV离开冲突栅格后其他AGV方可进入,即低优先级AGV的停车等待时间为AGV正常行驶通过一个栅格的时间。在节点冲突下,目标函数Tmax可按以下方法计算:在解决冲突的过程中AGV执行一次停车等待,则记录AGV此时搬运的包裹编号并更新nrjw、inTjr、outTjr和zorjt,然后将zorjt和nrjw代入式(2)可得Tmax。
3 改进差分进化算法
给定搬运包裹序列{π1,π2,…,πm},根据第2章的多AGV路径规划算法可为每个AGV规划出无冲突的搬运路径,此时,多AGV调度与路径规划问题的关键就在于如何生成高质量的搬运包裹序列,即多AGV调度问题。针对该问题,本章提出一种改进差分进化算法,设计了一种实数编码方案,使算法中的每个个体对应一种搬运包裹序列(调度序列),并采用多AGV路径规划算法为每个个体规划无冲突路径,进而生成调度序列与搬运路径的共同方案,以此作为评价依据对种群进行进化。在算法中,采用基于反学习的方法生成初始种群,运用自适应的变异和交叉概率对个体进行进化操作,提出一种动态差分进化策略来提高算法的收敛速度,并根据问题特征提出交换邻域和基于关键AGV的插入邻域进行局部搜索。改进差分进化算法的流程如图2所示。
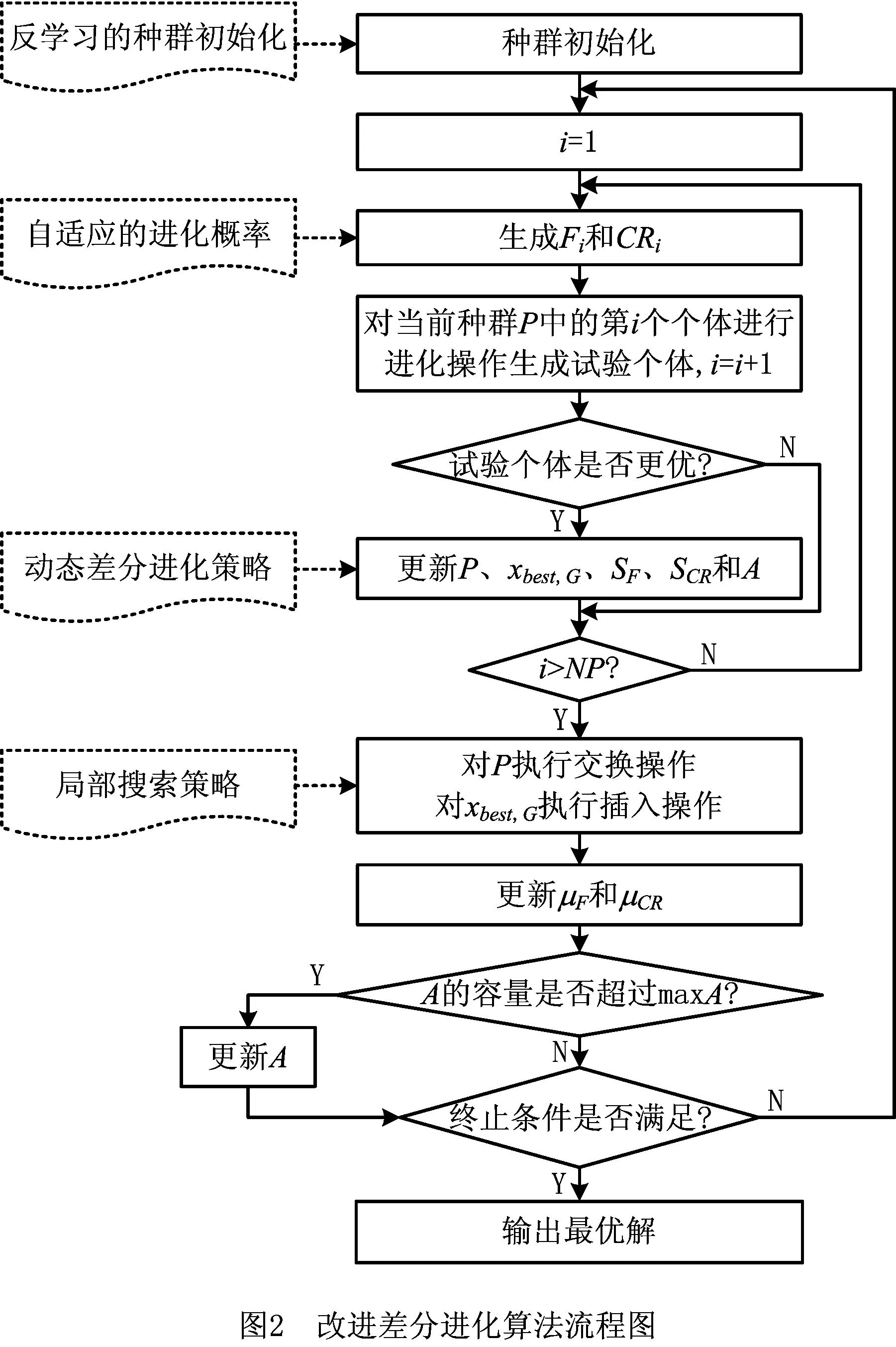
3.1 编码方案与种群初始化
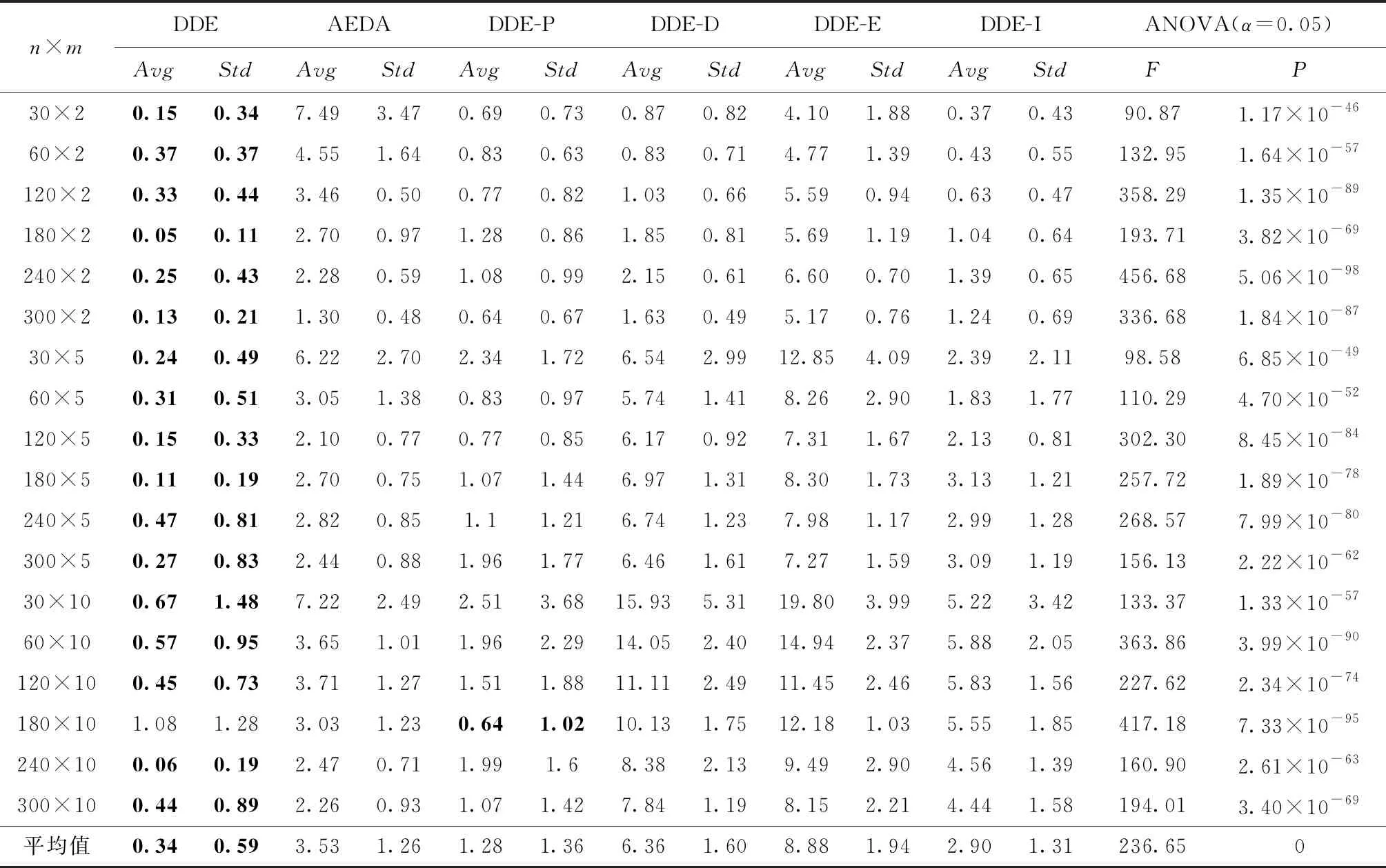
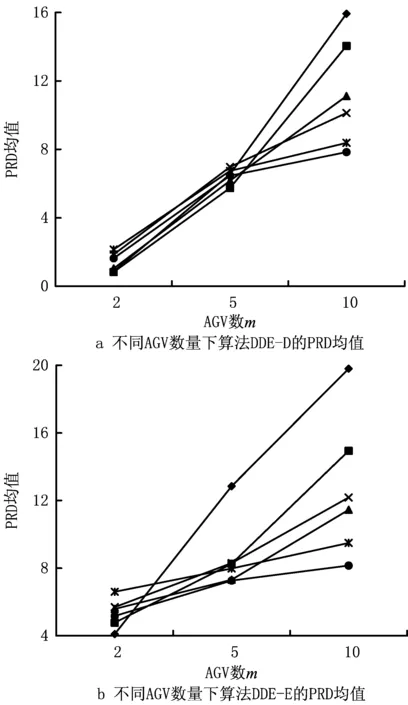
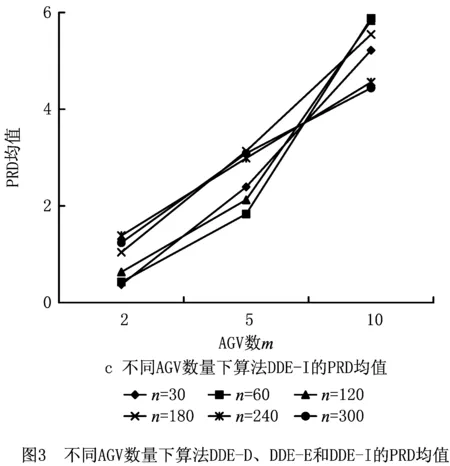
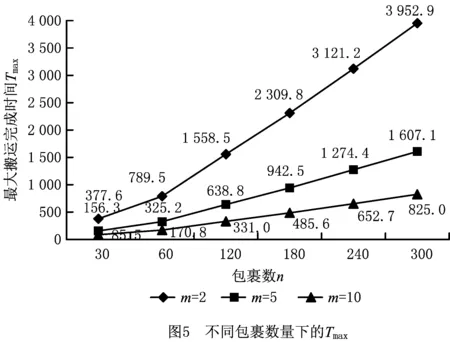
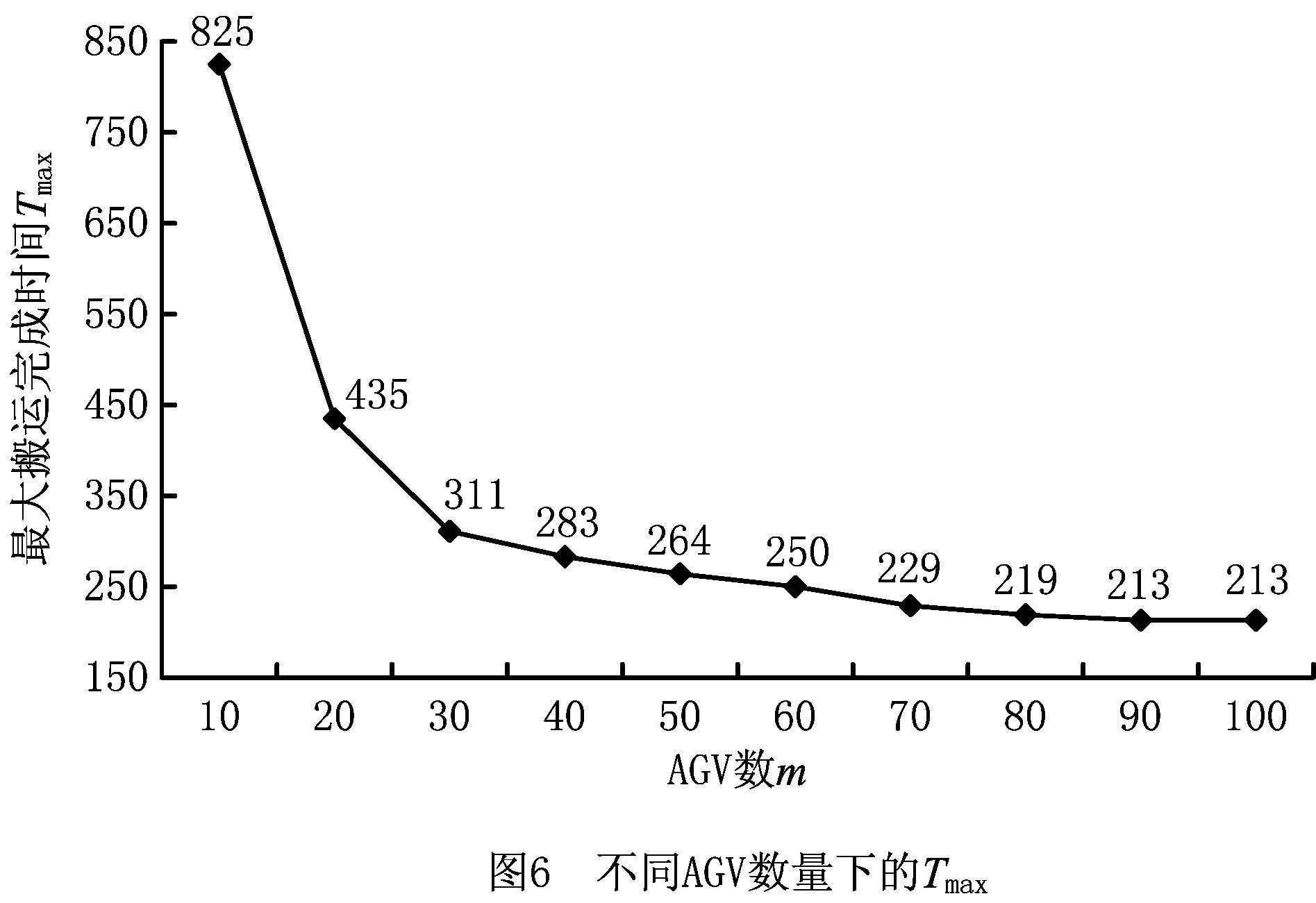
为适应DE的实数编码特征,本文设计了一种实数编码方案,具体如下:对于包裹数为n,AGV数为m的多AGV调度问题,定义种群个体编码为[x1,x2,…,xn],其中xi为实数,且需满足1≤xi 基于反学习的种群初始化步骤为:随机生成种群X;对种群X中的每个个体求其反向个体,组成种群OX;对种群X和OX中个体的适应值进行排序,选取适应值较高的个体组成初始种群。 本文改进差分进化算法涉及变异、交叉和选择3个操作算子,分别描述如下: (1)变异 本文采用JADE的“DE/Current-to-pbest/1”变异算子[19],计算公式如下: i=1,2,…,NP。 (3) 变异操作得到的个体,其元素值可能不可行,即超出规定范围[1,m+1),此时需要进行边界条件处理。对于不可行的元素vji,G,在可行域[1,m+1)中随机生成一个值代替当前值。 (2)交叉 按式(4)对变异生成的个体vi,G与原个体xi,G进行交叉操作[19],产生试验个体μi,G: i=1,2,…,NP,j=1,2,…,D。 (4) 式中:rand(j)表示[0,1]之间的随机数;rnbr(i)是属于(1,2,…,D)的随机整数,保证μi,G中至少有一个参数来自vi,G;CRi为自适应交叉概率,按照文献[19]提出的方法进行更新。 (3)选择 按照贪婪准则将试验个体μi,G与原个体xi,G进行比较,若μi,G的适应值更高,则用μi,G代替原个体xi,G,否则,保持原个体不变。适应值f的计算方法为:f=1/Tmax。另外,为了避免出现AGV闲置的情况,将存在闲置AGV的个体的适应值设为0,使其在进化过程中被快速淘汰。 标准DE算法在变异和交叉操作后会产生一个试验种群,进而对试验种群和原种群的个体进行一对一比较,选择较优个体进入下一代。这种进化策略存在以下不足:①对于试验个体,即使适应值较优,也不能立即参与到当代的进化操作中,而是要等到进入下一代;②即使试验个体的适应值高于xbest,G中个体的适应值,该优质个体也不能立即加入到xbest,G中。针对这两点,本文提出了动态差分进化策略,取消了试验种群,在生成试验个体后立即与原个体进行比较,若试验个体优于原个体,则直接用该试验个体代替原个体,更新种群P和xbest,G,以此来加快算法的收敛速度。 为了增强算法的局部搜索能力,针对本文的问题特征,采用交换邻域和基于关键AGV的插入邻域进行局部搜索。 (1)交换邻域 对于一个个体,随机选择两个位置并交换其中的元素,即随机交换两个包裹的搬运AGV或调换两个包裹在同一AGV中的搬运次序。例如个体[3.44,3.71,1.38,3.74,2.89,1.29],若位置3和6交换,则AGV1的搬运序列从6-3变为3-6。 (2)基于关键AGV的插入邻域 将搬运完成时间最大的AGV定义为关键AGV,表示为AGVjmain。AGVjmain的搬运完成时间直接影响Tmax,若能将AGVjmain搬运包裹序列中的包裹分配给其他AGV,则会降低Tmax。因此,本章提出了基于关键AGV的插入邻域,具体描述为:对于AGVjmain,顺序选择πjmain中的包裹,将其插入到非关键AGV的搬运序列中。基于贪婪准则,对于包裹πjmain(r),若执行插入后Tmax降低,则接受移动,否则重新选择非关键AGV并插入序列,直至所有的非关键AGV都被选择。插入过程中,若AGVjmain发生变化,则对新的πjmain执行上述操作。 基于以上的算法设计,改进DE算法的求解步骤如下: 步骤1输入算法参数,包括种群规模NP、最大迭代次数maxG和外部存档集的上限maxA等。 步骤2采用基于反学习的种群初始化方法生成种群P。 步骤3进化种群P。 步骤3.1 初始化进化个体数i=1; 步骤3.2 根据文献[19]所采用的方法生成Fi和CRi,对当前种群中的第i个个体进行变异、交叉和边界条件处理,生成试验个体,进化个体数i=i+1; 步骤3.3 运用多AGV路径规划算法为原个体和试验个体对应的调度解规划搬运路径,并计算适应值;若试验个体适应值较大,则直接代替原个体,并根据动态差分进化策略更新P、xbest,G、SF、SCR和A,否则,保持原个体不变; 步骤3.4 若进化个体数i达到种群规模NP,则转步骤4,否则转步骤3.2。 步骤4对种群P中所有个体执行交换操作,对xbest,G中的个体执行插入操作。 步骤5更新μF和μCR,若外部存档数据集A中个体数超过maxA,则随机移除超过的个体数;否则,保持A不变,更新迭代次数G=G+1。 为验证改进DE算法及其优化策略的有效性,以图1所示的自动化分拣仓库模型为仿真实例,展开数据实验。问题规模设置为包裹数n=30,60,120,180,240,300;AGV数m=2,5,10。根据问题规模将实验分为18组,每组随机生成30个算例。 本文设计的改进DE算法记为DDE,算法参数设置为:NP=40,maxG=500,maxA=40,v=1.5 m/s,l=1.5 m,Mtimes=50(执行插入操作的次数),tw=1 s,参考文献[19],令p=0.05,c=0.1。由于本文的多AGV调度问题对应无关并行机的调度问题,因此,设置了以下5种对比算法:①AEDA:文献[16]提出的用于求解无关并行机调度问题的自适应分布估计算法(算法参数与文献[16]保持一致),用来检验DDE的有效性;②DDE_P:变异概率和交叉概率为固定值F=0.5,CR=0.1,用来检验DDE自适应进化概率的有效性;③DDE_D:采用标准DE算法基于种群的进化操作,用来检验DDE动态差分进化策略的有效性;④DDE_E:局部搜索策略仅采用插入邻域,用来检验DDE交换邻域的有效性;⑤DDE_I:局部搜索策略仅采用交换邻域,用来检验DDE插入邻域的有效性。 以上算法均采用MATLAB编程实现,运行环境为Intel(R)Core(TM)i7-4510U/CPU 2.00 GHz 2.50 GHz/8.0 GB/MATLAB R2012a,算法性能从有效性和求解效率两方面衡量。本文采用相对偏离率(Percentage Relative Difference, PRD)来衡量算法有效性,计算公式如下: (5) 算法的PRD均值和标准差如表1所示。本节运用方差分析(Analysis of Variance,ANOVA)对每组实验进行PRD均值差异性的显著性检验,假设α=0.05,对应的F临界值为2.27。表1的最后两列给出了每组实验的F和P值。 表1 6种算法的PRD均值、标准差与ANOVA分析结果 由表1可得: (1)在180×10规模问题上,PRD均值的最小值由算法DDE-P取得,除此规模问题外,PRD均值的最小值均由算法DDE取得,并且算法DDE的PRD均值和标准差的平均值均为最低,说明DDE的寻优能力最强,且求解性能最稳定。每组实验进行ANOVA分析得到的P值均接近于0,且明显小于0.05,这也说明6种算法的求解质量存在显著差异。 (2)AEDA的PRD均值是DDE的平均10.38倍,说明DDE算法的求解效果优于AEDA算法。DDE-P、DDE-D、DDE-E和DDE-I的PRD均值分别是DDE的平均3.76倍、18.71倍、26.12倍和8.53倍,说明DDE算法的自适应进化概率策略、动态差分进化策略以及两种局部搜索策略均是有效的。为了更好地观察动态差分进化策略以及两种局部搜索策略的优势与AGV数量之间的关系,进一步给出了不同AGV数量下DDE-D、DDE-E和DDE-I的PRD均值变化趋势图(如图3)。由图3可知,当包裹数一定时,随着AGV数量的增加,DDE-D(图3a)、DDE-E(图3b)和DDE-I(图3c)的PRD均值都呈逐渐增大的趋势,这说明,随着AGV规模的增大,3种策略的优势会更加明显。 为了更直观地观察算法的收敛性能,在120×10实验组中随机选择一个算例,图4给出了6种算法的收敛曲线对比图。 由图4可知,DDE在第384代取得了最小值309,而AEDA、DDE-P和DDE-I分别在第425代、450代和491代收敛到了最小值326、311和320,收敛精度和速度均不及DDE;DDE-D和DDE-E分别在第286代和348代取得了最小值324和339,而DDE在第286代和348代分别收敛到313和310,且尚未充分收敛,因此,算法DDE的收敛速度和精度优于其他5种算法。 在算法求解效率方面,表2给出了算法在求解小中大3种规模问题,以及所有算例的平均CPU时间。由表2可知:AEDA的计算时间最长,这是由于AEDA的交换邻域是对优势个体中所有工件进行机器交换,而DDE则对每个个体仅执行一次交换操作,计算时间优于AEDA;DDE、DDE-P、DDE-D的计算时间相差不大,这是由于自适应进化概率以及动态差分进化策略并没有增加算法的复杂度,对算法效率影响不大;DDE的计算时间多于DDE-E和DDE-I,这是由于DDE同时执行两种局部搜索策略,但是DDE获得的解显著优于其他算法,并且对于300个包裹10个AGV的问题,DDE也能在340 s内取得问题解,针对离线的多AGV调度与路径规划问题,可以满足实际应用需要。 表2 算法的CPU时间 s 包裹数n和AGV数m是本文问题的两个关键参数,本节分析这两个参数对算法性能的影响。 为了分析包裹数n的影响,本文采用DDE求得18个实验组的Tmax,其平均值如图5所示。由图5可知,当m一定时,随着n的增加,Tmax基本呈线性增长趋势,说明DDE算法的求解性能稳定,有良好的扩展性。为了分析AGV数m的影响,设置了n=300的10组实验,其中m分别为10,20,…,100。每组随机生成10个算例,用DDE求解,每组算例的Tmax平均值如图6所示。易见,当n一定时,随着m的增加,Tmax呈下降趋势,但下降的幅度逐渐减小。原因分析如下:增加AGV数虽然能够减少搬运时间,但AGV间发生冲突的概率也增加了,进而AGV的停车等待时间增多,利用率降低。因此,需要根据仓库容量和包裹数合理确定AGV的数量,实现资源的有效利用。 为进一步检验本文的多AGV路径规划算法和DDE算法性能与AGV数目的关系,设置对比算法DDE-O,该算法的AGV优先级为随机赋值,而不是基于本文提出的优先级规则。引入偏离率R比较DDE和DDE-O求解性能的差异, (6) R的变化趋势如图7所示,可以看出:①R>0,说明算法DDE的求解性能优于DDE-O,这表明本文的多AGV路径规划算法是有效的。②随着AGV数的增加,R先增加后降低。这是由于当AGV数目较少时,发生冲突的概率小,因而两种算法的求解性能差别较小;随着AGV数目的增加,发生冲突的概率增加,本文路径规划算法的冲突消解策略强化了算法DDE的优势;但当AGV数量增加到一定程度时,由于发生冲突的概率较大,多AGV系统基本处于饱和状态,此时,算法DDE的优势开始下降。这说明,当AGV数量超过一定限度时,无论用DDE还是DDE-O,都将造成资源浪费,因而要想实现高效分拣,在进行调度和路径规划的优化之外,还需要合理地确定AGV的数量。 本文针对自动化分拣仓库中多AGV调度与路径规划问题,以最小化最大搬运完成时间为优化目标展开研究。首先,根据自动化分拣仓库多AGV、多分拣台、多包裹的特征,设定了一个自动化分拣仓库的基本模型,并针对路径规划问题,提出了AGV优先级并设计了无路径冲突的多AGV路径规划算法。进而,针对调度与路径规划的综合优化问题,设计了一种改进差分进化算法。算法采用反学习的方法生成初始种群,运用自适应的变异和交叉概率对个体进行进化操作;此外,为了提高算法的收敛速度,提出了一种动态差分进化策略,并根据问题特征提出了交换邻域和基于关键AGV的插入邻域,通过局部搜索来增强算法的搜索能力。最后,基于大量随机生成的算例展开数据实验,实验结果表明,对于各种问题规模的随机算例,本文算法均具有良好的求解质量和计算效率,且本文算法的求解性能稳定,具有良好的扩展性。有关问题参数的实验结果表明,当AGV数量超过一定限度时,本文算法和对比算法均产生了资源浪费,因而应根据仓库面积以及包裹数量合理配置AGV的数量,而有关AGV合理数量的关键影响因素及其解析分析将是下一步研究的方向。
3.2 差分进化算子

3.3 动态差分进化策略
3.4 局部搜索策略
3.5 算法步骤
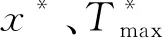
4 数据实验
4.1 实验设计
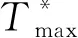
4.2 实验结果与分析


4.3 问题参数分析

5 结束语

