可调加工时间炼钢-连铸的灰狼优化调度算法

彭琨琨,李新宇,高 亮,邓旭东

(1.武汉科技大学 管理学院,湖北 武汉 430065； 2.华中科技大学 机械科学与工程学院,湖北 武汉 430074)

0 引言

钢铁工业为很多重要工业提供原材料，是国民经济重要的基础产业。目前，我国钢铁工业正面临着高端供给不足等问题。炼钢-连铸(Steelmaking-Continuous Casting, SCC)是钢铁工业生产中的瓶颈[1]，高效的SCC调度算法可较大地提高钢铁工业的生产效率。SCC调度问题是一个复杂的工业调度问题[2]，属于NP难组合优化问题。因此，该研究具有重要的工程意义和理论价值。

已有SCC调度算法中，智能优化方法得到了广泛应用，例如，文献[3]和文献[4]分别提出了求解SCC调度和重调度的果蝇优化算法，文献[5]设计了差分进化算法，在已有的SCC智能优化调度算法中，人工蜂群算法[6-7]得到了较多关注。此外，拉格朗日松弛方法[2]和启发式[8-9]也吸引了很多研究。

当前SCC调度算法的研究很多都将连铸阶段的加工时间视为固定。然而，实际生产过程中，连铸机的加工速度可在一定范围内调整，即炉次加工时间在一定范围内调整[10]，这可增加生产和调度的柔性，相应的SCC调度问题称为可调加工时间SCC调度问题。与考虑固定加工时间SCC调度问题研究相比，当前针对可调加工时间SCC调度的研究相对较少。例如，文献[10]设计了针对考虑允许可跳跃阶段的可调加工时间SCC调度的改进遗传算法，文献[11]研究了拉格朗日启发式重调度方法。

灰狼优化(Grey Wolf Optimizer, GWO)算法是一种较新且高效的群智能优化算法，由Mirjalili等[12]于2014年提出，目前已引起很多学者的关注，已成功求解铸造生产调度[13]、焊接车间调度[14-15]等NP难组合优化问题。

本文借鉴GWO算法的优良特性，结合可调加工时间SCC调度的问题特征，研制了求解该问题的GWO算法。从解码方法、种群初始化、基于多操作的搜索算子及重启操作等角度着手设计，较大地提升了GWO算法解决可调加工时间SCC调度的求解性能。

1 可调加工时间炼钢-连铸调度问题

SCC生产过程主要包含炼钢阶段、精炼阶段和连铸阶段3个顺序的生产阶段[1]。炼钢阶段主要利用转炉将高炉的铁水转化为钢水，去除某些杂质；精炼阶段使用精炼设备对钢水进行精炼，进一步去除某些杂质，调节钢水的成分和温度，该阶段可能包含多个精炼阶段，称为多重精炼；而连铸阶段则使用连铸机将精炼阶段生成的钢水连续浇铸生成板坯[9,16]。炼钢阶段和精炼阶段的最小工作单元为炉次，相当于车间调度问题中的工件，而连铸阶段的最小工作单元为浇次，浇次为一组炉次的集合[16-17]。如图1所示为SCC生产过程简单示意图。图中：从左往右依次为炼钢阶段、3个精炼阶段、连铸阶段。其中：炼钢阶段包含3台转炉，分别为1#LD、2#LD和3#LD；第1个精炼阶段包含3台精练设备，分别为1#RH、2#RH和3#RH，类似地，第2、3个精炼阶段也各自包含3台精练设备；连铸阶段包含3台连铸机，分别为1#CC、2#CC和3#CC。

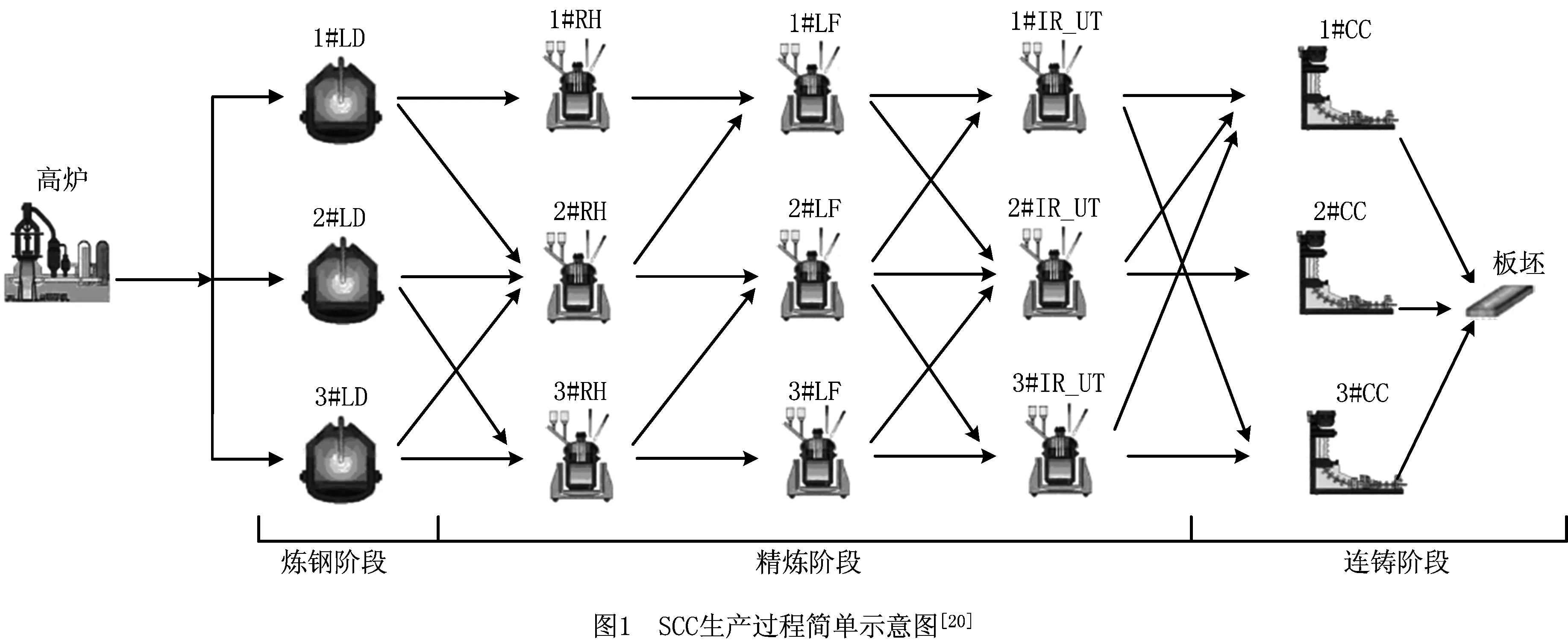
可调加工时间SCC调度问题可描述如下，给定一定的假设条件(例如已事先给定各浇次在连铸机上的分配情况等)，要求编制一个满足实际生产状况和多个复杂约束的优化调度方案，其中各炉次在连铸阶段的加工时间可在一定范围内调整[10]，该优化调度方案给出了在炼钢阶段、精炼阶段和连铸阶段，各炉次分别在何时开工、完工，以及各炉次在炼钢阶段和精炼阶段在哪台机器上加工。本文考虑的优化目标为最小化平均逗留时间、浇次的提前连铸时间、浇次的滞后连铸时间，考虑的复杂约束包括：同一个浇次内的炉次在连铸阶段必须连续加工；对于在同一台机器上加工的两个炉次，只有在前者完成之后，后者才能开始加工等约束[1]。

2 解决可调加工时间炼钢-连铸调度问题的灰狼优化算法

基本GWO算法是针对连续优化问题而设计的，不能直接求解可调加工时间SCC调度问题这一组合优化问题，本文专门裁剪了GWO算法来解决该问题。下面首先介绍了基本GWO算法，随后给出了本文设计的GWO算法，依次从编码、新解码方法、种群初始化、社会等级分层、基于多操作的搜索算子、重启操作、算法框架等7个方面来进行详细说明。

2.1 基本灰狼优化算法

基本GWO算法[12]将一个初始灰狼种群作为搜索起点，接着执行社会等级分层，随后执行搜索算子、社会等级分层的循环进化操作，直至达到算法终止条件[12]。其主要思想是不断更新种群中的最好的3个解：最好解α、次好解β、第三好解δ，并利用它们来引导其他解的进化搜索。

2.2 编码

本文使用了炉次排序对解进行编码，炉次顺序对应于炉次的操作顺序，编码中的每一个数字对应一个炉次。

2.3 解码方法

解码是实现解与调度方案之间映射的桥梁，对于GWO算法非常关键。本文考虑了问题特征，基于文献[1]和文献[9]的工作，提出一种新的解码方法，包含正向解码、连铸阶段加工时间调整、反向解码3个阶段。本文的编码方法与文献[1]编码方法的不同主要在于：文献[1]中的编码方法将连铸阶段加工时间视为固定，仅包括正向解码和反向解码，而本文的编码方法在文献[1]中的编码方法基础上，考虑了连铸阶段加工时间可调，解码时在正向解码与反向解码之间增加了连铸阶段加工时间调整。具体描述如下：

步骤1正向解码。

在炼钢阶段和精炼阶段，按编码中炉次排序依次选择炉次，为其选择最早的可用机器，在连铸阶段，按各浇次中的炉次顺序加工。

步骤2连铸阶段加工时间调整。

步骤2.1 连铸阶段加工时间调整I。

在连铸阶段，对每个浇次，如果任意两个连续炉次(假设i和i+1)之间存在断浇，则炉次i的加工时间增加min{Δti,CBi,i+1}，其中：Δti为炉次i的当前加工时间最大可增加值，CBi,i+1为炉次i和i+1之间的断浇时间。随后更新CBi,i+1和Δti。

步骤2.2 连铸阶段加工时间调整Ⅱ。

在连铸阶段，对每个浇次，如果不存在断浇，则转下一浇次，否则，执行以下步骤：

(1)计算该浇次的断浇时间之和，记为CBSum。

(2)进而计算addAver=CBSum/n，其中n为该浇次中首炉次至最后一个断浇之间的炉次数目。

(3)对前n-1个炉次(假设为j)，将其加工时间增加min{Δtj,addAver}，将第n个炉次的加工时间增加min{Δtn,CBSum-addAver×(n-1)}，随后更新CBi,i+1。

步骤3反向解码。

步骤3.1 在连铸阶段，对每个浇次，如果不存在断浇，则转下一浇次，否则，从该浇次的倒数第二个炉次开始，同时右移其完工时间和开工时间，使其完工时间等于下一个炉次的开工时间。

步骤3.2 在精炼阶段，对所有炉次，按编码中的炉次顺序，从倒数第一个炉次开始，将其完工时间和开工时间右移。

步骤3.3 在炼钢阶段，对所有炉次执行类似步骤3.2的操作。

2.4 种群初始化

好的初始种群很可能有助于加快GWO算法的收敛。本文设计了如下方法以得到具有一定质量且保持多样性的初始种群。

步骤1根据事先定义的浇次的计划开工时间及每个浇次中各炉次的顺序，获得每个炉次在连铸阶段的开工时间，按非降排序[1]。得到的炉次排列记为P1。

步骤2对P1重复执行N次Multiswap算子，生成的N个解记为P2,…,PN+1。

步骤3对P1重复执行N次Swap算子，生成的N个解记为PN+2,…,P2N+1。

步骤4对P1重复执行N次Pairwiseexchange算子，生成的N个解记为P2N+2,…,P3N+1。

步骤5对炉次进行随机排序，重复执行M-3N-1次，生成剩余的M-3N-1个初始解。

2.5 社会等级分层

更新历史最好解α、历史次好解β及历史第三好解δ，即若当前解Ptj优于α，设置δ=β，β=α，α=Ptj；若Ptj仅优于β，设置δ=β，β=Ptj；若Ptj仅优于δ，设置δ=Ptj。

不同于基本GWO算法，只有在整个种群更新完毕后，才执行社会等级分层。在本文GWO算法中，一旦得到一个新解，就执行社会等级分层。目的在于及时更新α、β、δ，提高GWO算法的集中性。

2.6 基于多操作的搜索算子

搜索算子是GWO算法的关键和核心，直接决定了GWO算法的搜索性能。本文专门设计了一种基于多操作的搜索算子，可在一定程度上实现集中性和多样性的平衡。

给定当前解Ptj，基于多操作的搜索算子可描述如下：

步骤1在区间[0,1]内生成一个随机数rd1，若rd1<1/3，转步骤3执行基于部分映射交叉操作(Partially Mapped Crossover, PMX)的操作算子1；若1/3≤rd1<2/3，转步骤4执行基于PMX的操作算子2；若2/3≤rd1<1，转步骤5执行局部搜索算子。

步骤2在区间[0,1]内生成一个随机数rd2，若rd2<1/3，设置St=α；若1/3≤rd2<2/3，设置St=β；若2/3≤rd2<1，设置St=δ。

步骤3基于PMX的操作算子1。

步骤3.1 执行步骤2。

步骤3.2 以St和Ptj为父代个体执行PMX，从两个子代个体中随机选择一个，记为Pt+1,j。

步骤4基于PMX的操作算子2。

步骤4.1 执行步骤2。

步骤4.2 对St执行NNSize次Multiswap算子，得到NNSize个新解，将其中的最好解记为Sp。

步骤4.3 以Sp和Ptj为父代个体执行PMX，从两个子代个体中随机选择一个，记为Pt+1,j。

步骤4.4 如果Sp优于Ptj和Pt+1,j，则设置Pt+1,j=Sp。

步骤5局部搜索算子。

步骤5.1 设置t=1。

步骤5.2 对Ptj执行NNSize次Multiswap算子，得到NNSize个新解，将其中的最好解赋值给Ptj。

步骤5.3 设置t=t+1。若t≤T，转步骤5.2；否则，设置Pt+1,j=Ptj。

基于多操作的搜索算子具有以下4个优点：(1)对3种不同操作以等概率选择执行。同时，执行基于PMX的操作算子1和2时，从两个子代中随机选择一个来更新当前解。这可探索不同的搜索路径，提升了GWO的多样性。

(2)基于PMX的操作算子1可学习α，β，δ的优良特性。

(3)基于PMX的操作算子2可学习α，β，δ较好邻域解的优良特性，在其邻域内进行一定的探索。

(4)局部搜索算子可对当前解的邻域执行搜索，提升了GWO算法的集中性。

2.7 重启操作

为提升GWO算法的多样性，进一步设计了一种重启操作。其主要思想是，若某一个解(记为Pgj)连续多代未改进，它可能陷入了局部最优。以等概率选择3种操作算子中的一个，对它执行该算子，希望将其引导至新的尚未搜索过的区域。该重启操作类似于文献[6]中的侦察蜂阶段。具体地，该操作可描述如下：

步骤1若解Pgj连续多代仍未改进，转步骤2。

步骤2对Pgj以等概率(即1/3)执行如下3种操作之一：①连续执行3次Multiswap算子；②连续执行3次Swap算子；③连续执行3次Insert算子。将得到的新解记为Pnew。

步骤3设置Pg+1,j=Pnew。

2.8 算法框架

给定GWO算法的参数：种群规模M，连续未改进的允许最大迭代次数NI，执行Multiswap算子的次数NNSize，局部搜索算子的最大循环次数T，如图2所示为GWO算法的流程图。由图2可以看出，GWO算法首先需要设置算法参数，然后利用两种初始化策略生成具有一定质量和多样性的初始种群，并对种群执行社会化等级分层操作。随后，对种群中每个个体分别执行基于多操作的搜索算子、对种群执行社会化等级分层操作、对种群执行重启操作，循环执行这3个步骤，直至达到GWO算法的终止条件(允许的最大CPU运行时间或允许最大迭代次数)，最后输出GWO算法搜索到的历史最好解。

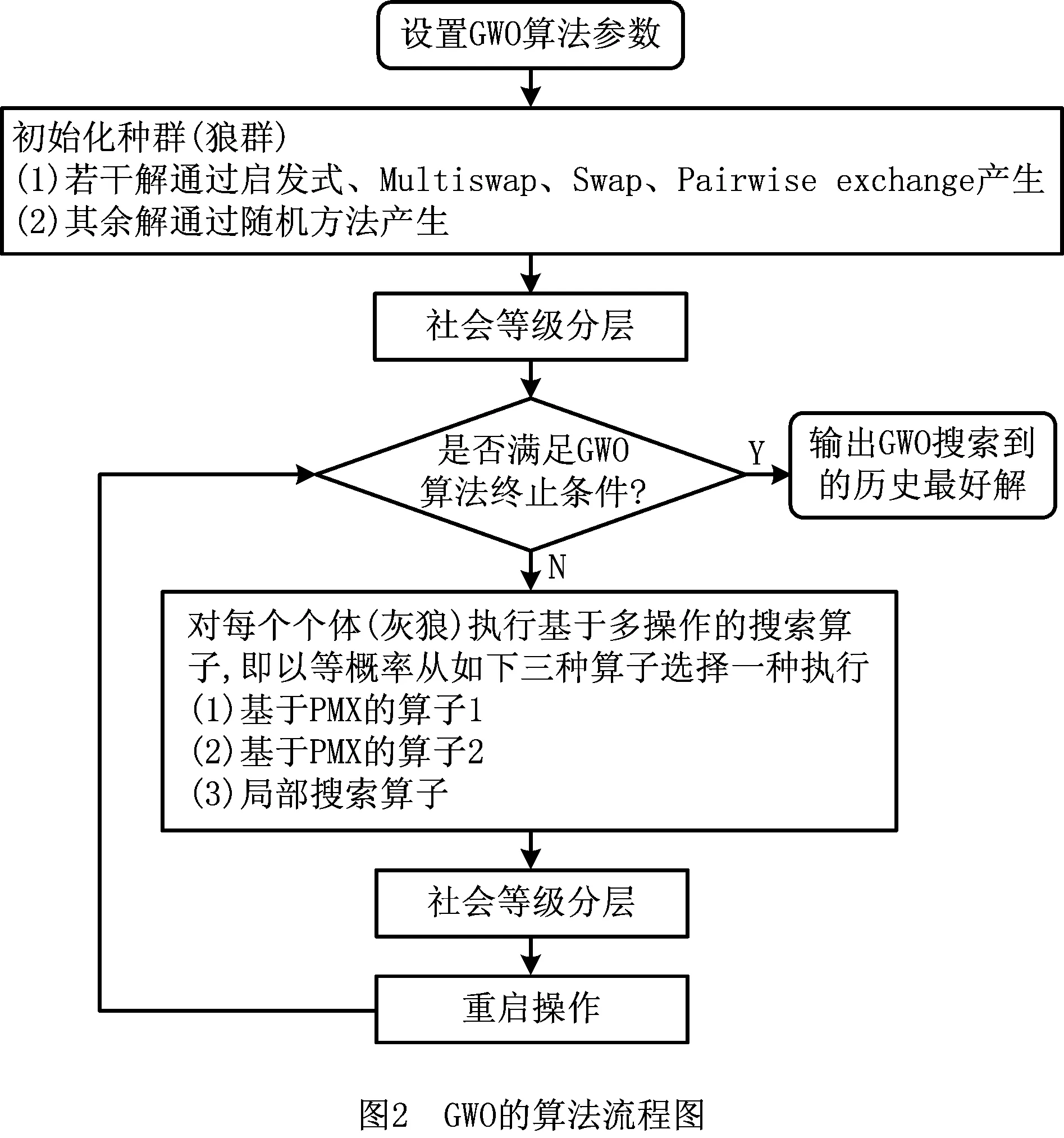
3 实验与结果

为验证所提GWO算法的高效性，本章将其与文献中的4种调度算法进行了对比，包括两种有效的SCC调度算法和两种有效的车间调度算法：改进人工蜂群算法(Improved Artificial Bee Colony, IABC)[6]、果蝇优化算法(Fruit Fly Optimization, FOA)[3]、迭代局部搜索(Iterated Local Search, ILS)[18]、遗传算法(Genetic Algorithm, GAR)[19]。

本文使用C++对算法在Visual Studio 2013中进行编程，在Windows 7操作系统下配置为2.13 GHz和2 G内存的计算机上执行。GWO算法的参数设置如下：M=30，NI=50，NNSize=5，T=5。每种对比算法都使用了本文的编码和解码方法。对于每个算例，每种算法独立运行10次，并计算这10次运行的平均目标函数值。使用相对百分比增加(Relative Percentage Increase，RPI)来评价算法性能，其中使用了每种算法的10次的平均值来计算RPI，即

(1)

式中：fC为对比算法C独立运行10次的平均值，C是指GWO、IABC、FOA、ILS、GAR，fbest是指对比算法中的最好值。

3.1 算例说明

使用文献[1]中的算例生成方法生成30个算例。共有3台转炉，5台精炼炉，4台连铸机。每个连铸机加工3～4个浇次，而每个浇次包含8～12个炉次。炼钢阶段到精炼阶段的转移时间、精炼阶段到连铸阶段的转移时间均在区间[10,15]内取值。炉次j在炼钢阶段、精炼阶段的加工时间分别在如下范围内取值：PT1j=38，PT2j∈[36,50]，炉次j在连铸阶段的一般加工时间在如下范围内取值：PT3j∈[38,44]，而PT3j的最小与最大加工时间分别为0.9PT3j和1.1PT3j。

3.2 基于多操作的搜索算子的重要性

为验证基于多操作的搜索算子对于GWO算法的重要性，本节执行实验来对比GWO算法与使用另外两种搜索算子的GWO算法。其中，第一种GWO算法使用基于PMX的操作算子1，记为GWOPMX算法，而第二种GWO算法使用文献[15]中的搜索算子(记为shift算子)，记为GWOs，GWOPMX算法和GWOs算法的其余成分与GWO算法相同。使用了3种算法终止条件进行实验，即CPU时间分别为10 s、20 s和30 s。

表1给出了CPU时间为10 s下，3种对比算法的RPI。由表1知，在CPU时间10 s下，GWO算法的性能明显好于GWOPMX算法和GWOs算法，GWO算法的RPI平均值为0.01%，在30中的29个测试算例上，GWO算法的RPI为0，而GWOPMX算法和GWOs算法的RPI平均值分别为4.50%和15.12%。表2给出了CPU时间为20 s和30 s下，3种对比算法的平均RPI。由表2可知，在CPU时间为20 s和30 s下，GWO算法依然优于GWOPMX算法和GWOs算法，3种对比算法的平均值分别为0，3.65%，15.50%。当CPU时间为20 s时，3种对比算法的RPI平均值分别为0，3.80%，15.39%。而在CPU时间为30 s下，3种对比算法的RPI平均值分别为0，3.50%，15.60%。该实验对比表明基于多操作的搜索算子优于PMX和shift算子，从而说明其有效性。

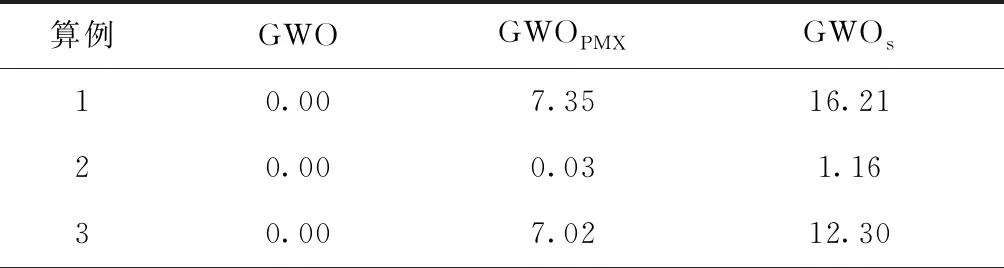
表1 CPU时间为10 s下的不同搜索算子的RPI对比结果

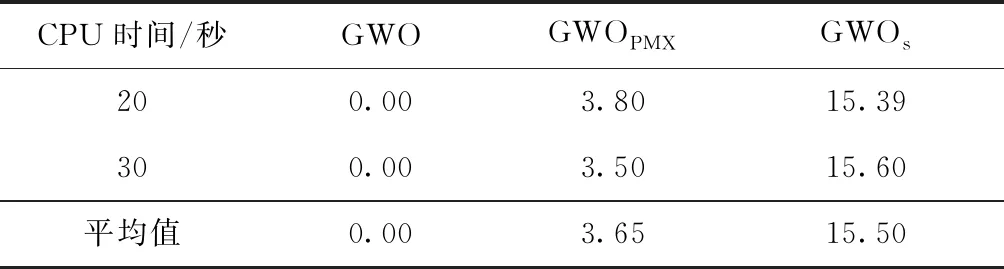
表2 CPU时间为20 s和30 s下的不同搜索算子的平均RPI对比结果

3.3 与4种调度算法的对比

本节将GWO算法与IABC、FOA、ILS、GAR进行了对比，同样使用了3种算法终止条件，即CPU时间分别为10 s、20 s和30 s。IABC、FOA、ILS、GAR的参数设置与相应文献相同，CPU时间为10 s下的对比结果如表3所示。由表3可知，在CPU时间为10 s下，GWO优于IABC、FOA、ILS、GAR，GWO的平均RPI仅为0.79%，而IABC、FOA、ILS、GAR的平均RPI分别为1.26%、2.15%、4.32%和12.00%。

表4给出了CPU时间为20 s和30 s下5种对比算法的平均RPI。根据表4，GWO仍然优于IABC、FOA、ILS、GAR，GWO的平均值为0.80%，而IABC、FOA、ILS、GAR的平均值分别为1.56%、1.98%、3.34%和9.91%。具体地，在CPU时间为20 s下，GWO算法优于IABC、FOA、ILS、GAR，它们的平均RPI分别为0.78%、1.46%、1.95%、3.61%和10.35%。而在CPU时间为30 s下，GWO算法依然优于IABC、FOA、ILS、GAR，相应的平均RPI分别为0.81%、1.65%、2.01%、3.07%和9.46%。由此说明GWO算法可高效地解决可调加工时间SCC调度问题。

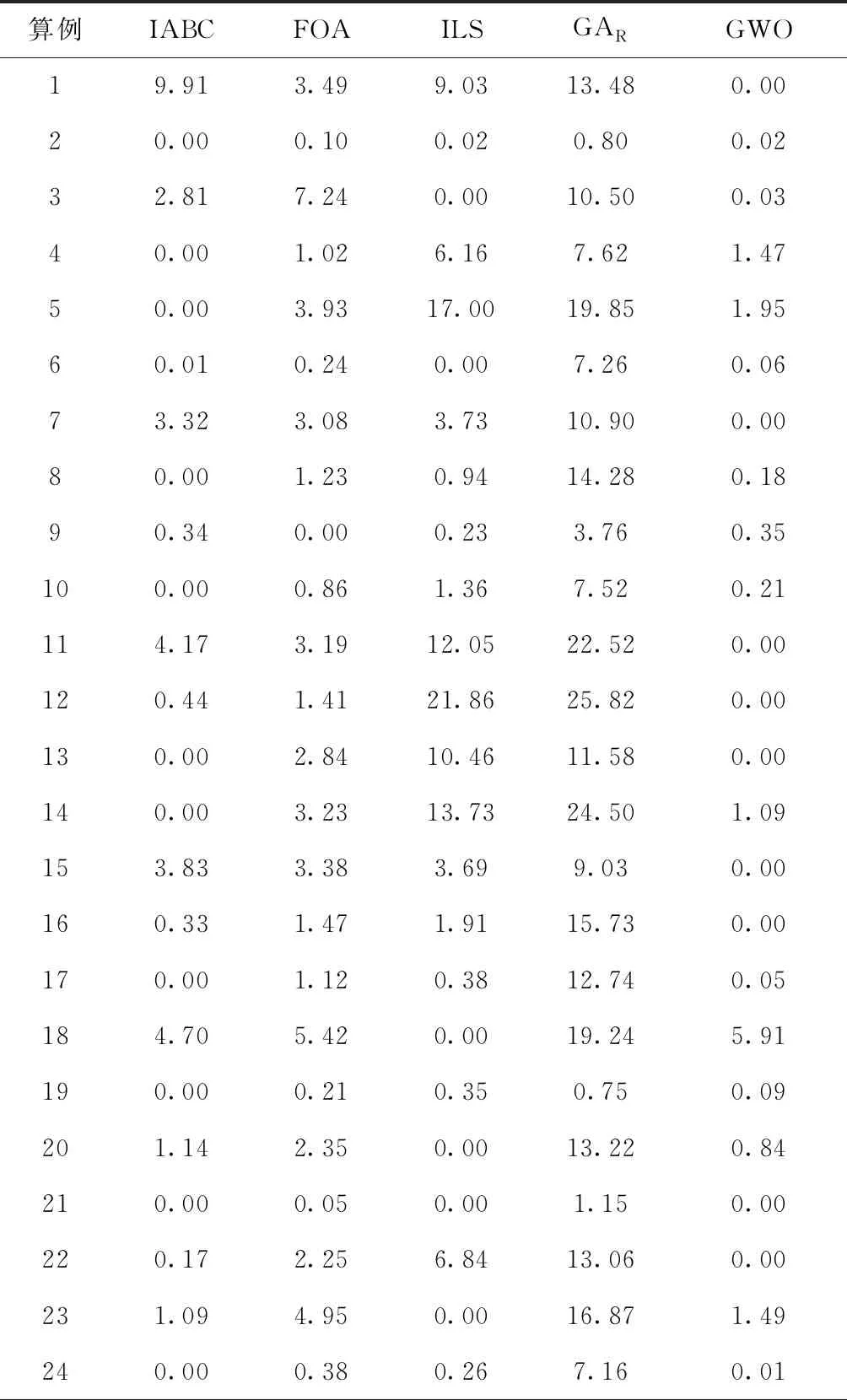
表3 CPU时间为10 s下的算法RPI对比结果

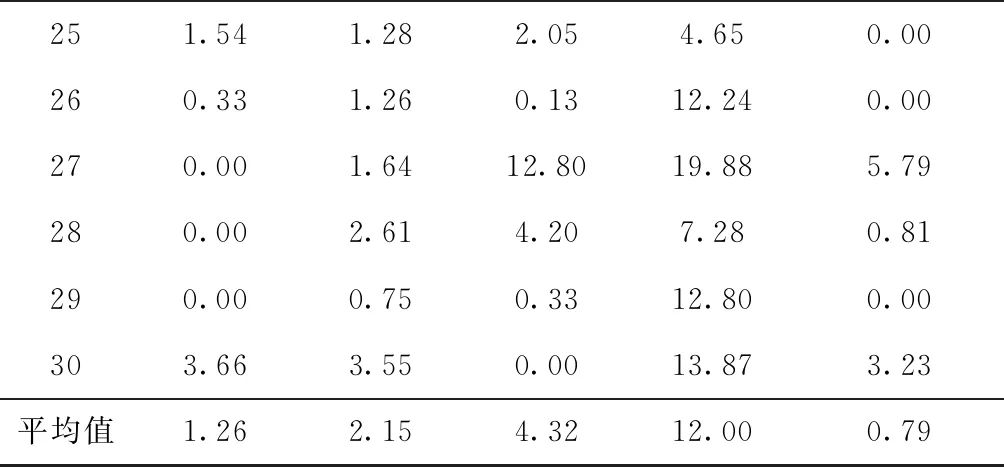
续表3

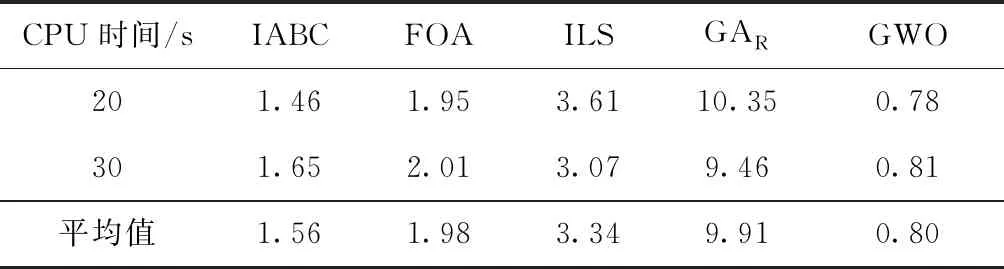
表4 CPU时间为20 s和30 s下的算法平均RPI对比结果

4 结束语

本文提出了解决可调加工时间SCC调度问题的高效GWO算法。利用连铸阶段加工时间可调这一特性，设计了新解码方法。并研究了种群初始化方法，可得到具有一定质量和多样性的初始种群。其次，研制了高性能的基于多操作的搜索算子，可在一定程度上实现集中性和多样性的平衡。此外，开发了重启操作以帮助GWO算法跳出局部最优。通过实验对比验证了GWO算法的有效性。本文提出的解码方法、种群初始化及基于多操作的搜索算子也可用于求解可调加工时间SCC调度问题的其他算法，此外，GWO算法也可用于解决其他调度问题，如SCC重调度[20]、混合流水车间重调度[21]等。