基于使用可靠性区域粒度的产品保修期优化决策

揭丽琳,刘卫东,2+

(1.南昌航空大学 无损检测技术教育部重点实验室,江西 南昌 330063; 2.南昌大学 机电工程学院,江西 南昌 330031)

0 引言

产品保修设计既是控制、降低产品保修成本的一种重要手段，又是提高消费者售后服务满意度和企业利润水平的有效途径。以保修期为核心要素的保修策略已逐渐成为新的市场竞争焦点。科学合理地制定产品的保修期，不但要综合考虑企业的保修成本投入以及在目标市场的销售价格，而且要考虑产品的质量属性。可靠性已成为衡量产品质量属性的核心指标，也是影响保修期设计的关键因素[1-3]。此外，分布于不同地理区域的产品，由于实际所处的工作条件和使用时间不一致，导致其使用可靠性呈现显著的差异[4]。因此，从使用可靠性的角度对产品保修期进行优化设计，有助于更精准地制定符合客观实际的保修期，从而有效提升市场竞争力和企业的保修效益。

基于可靠性的保修期研究主要涉及可靠性的评估以及如何应用所掌握的可靠性信息研究制定科学的保修期等方面。近年来，关于产品可靠性的评估和基于可靠性的保修期设计的研究逐渐增多，但仅有少量研究成果涉及分析使用可靠性与地理区域差异的关联性以及应用于设计相关产品的保修期。目前，主要采用可靠性试验、组件的数值和概率模拟以及现场数据的统计分析等手段对产品可靠性进行评估预测[5-7]。其中，基于可靠性试验的评估方法使用广泛，但由于其耗时长、成本昂贵的特性，不适用于高可靠、长寿命产品；而基于组件的数值和概率模拟的评估方法在一定程度上弥补了前者的不足，但是对于存在多种失效机理的复杂产品，仍具有评估精度低的缺点，因此上述两种评估方法在许多应用领域均受到限制。相较之，采用现场数据的统计分析法则具有评估精度高、耗时短、成本低的特性。为此，国内外很多学者关注了运用现场返回数据进行可靠性评估的问题，并取得了一定的研究成果。比如，Al-Garni等[8-9]均选取现场数据，并分别运用Weibull和Gamma分布模型对比研究了空调系统的可靠性；Lu[10]提出一种基于早期现场故障保修数据的可靠性预测方法，以达到减少召回车辆数量的目的；Ion等[11]运用维修部门提供的短期、早期故障的保修数据对消费电子产品的可靠性进行实时评估，并判断其可靠性是否维持在一定水平；Altun等[12]通过采用现场返回数据构建了一种改进的基于变化点的可靠性预测模型，从而预测高容量复杂电子产品在其保修期内的可靠性性能；蔡忠义等[13]将外场数据与加速寿命数据融合提出一种改进的可靠性评估技术，试验数据显示该方法的评估精度要比传统模型更高；史晓平[14]等对总体样本容量未知，产品寿命服从指数分布的维修纪录数据进行了统计分析，给出了可靠度、平均寿命的估计。Suik等[15]通过采用保修期内的故障数据，定性分析研究了循环流化床锅炉的压力件、燃料供应系统以及底灰系统的可靠性。Gurel等[16]结合液晶电视保修期的研究，对售后服务部门提供的产品寿命数据，采用威布尔分布模型和线性回归分析方法进行失效率的估计。而应用保修期内的售后故障数据进行空调产品可靠性评估的研究极少，仅有刘卫东等[17]提出了一种基于聚类分析和时间浓缩的故障数据分类处理方法，并应用于空调可靠性水平的定量估计，但该研究没有考虑使用可靠性与不同地理区域以及固有可靠性之间的定量关系。

从目前基于现场数据统计分析的可靠性评估的研究现状来看，还没有充分利用大量的售后故障数据定量评估不同区域的产品使用可靠性，既无法建立反映使用可靠性与地理区域间定量关系的数学模型，也无法获得固有可靠性与使用可靠性两者间的函数关系式，并将其应用于确定保修期的定量研究。此外，大多数研究都是针对某一特定分析的问题和具体数据而提出的具体模型和方法，缺乏对一般性模型和方法的深入探讨和研究。

现有保修期设计研究大多都局限于产品出厂时的固有可靠性，主要采用最优化方法从保修成本最小化或利润最大化角度提出了一系列的决策模型。基于保修成本最小化角度，如Chien[18]分别从制造商和消费者的视角出发，以保修成本最小化为目标分析确定产品的最优保修期与更换年限。Ambad等[19]以产品可靠性增加和保修成本最小为目标，构建了平均故障间隔时间与保修成本加权的目标优化函数，并利用遗传算法求解最优的保修期。刘卫东等[20]应用可靠性增大(Army Material System Analysis Activity, AMSAA)模型构建固有可靠性增长模型，进而建立了由保修费用和保修效益函数两部分组成的保修利益目标模型，并求解出最优的产品保修期。基于利润最大化角度，如Murthy[21]将可靠性决策与市场变量相结合，并综合考虑产品可靠性、价格和保修期的影响，建立了利润最大化目标函数。Wu等[22]进一步发展了Teng等[23]构建的质量与价格的双参数决策模型，通过将模型中的质量水平替换为保修期长度，构建了一种改进的产品保修期决策模型，并优化选择产品的价格和保修期使企业利润最大化。Decroix[24]系统分析了供不应求耐用商品的最优保修期、可靠性和价格的关系，指出每个制造商可以不依赖价格和竞争者行为来设计产品可靠性和保修期，并讨论了不同市场类型对保修期和可靠性的影响。Wang等[25]综合考虑保修服务质量对顾客满意度和重复购买的影响，重构了产品需求函数，并由此建立了一种改进的成本函数和保修决策模型。Huang等[26]通过分析产品的可靠性、保修期和价格对销售量、生产成本和保修服务成本的影响，构建了贴现利润最大化决策模型，并假设采用免费更换保修策略时，分别就保修期和价格在不随时间变化的稳态市场、随时间变化的动态市场以及改变产品生命周期的条件下，运用数值分析法确定保修期、价格和可靠性的最优组合。Darghouth等[27]在文献[26]的基础上，针对带有维修服务协议且仅有制造商提供维修服务的新产品，建立了一种联合优化产品保修期、可靠性和价格的贴现利润最大化目标模型，并考虑了4种不同维修协议选项下的稳态市场和动态市场，分别推导出每种情况所必需的最优条件，优化选择保修期、可靠性和价格的组合策略使得制造商获利最大。

上述保修期设计研究中均假设产品出厂时的固有可靠性为常量，既没有考虑持续质量改进导致的固有可靠性增长，也没有考虑使用可靠性呈现的显著区域差异。而国内外从可靠性增长的角度设计保修期的研究极少，仅有刘卫东等[28]进一步挖掘产品固有可靠性增长的价值，并应用于构建空调保修期优化分析系统动力学模型。但该研究更多关注的是空调出厂时的固有可靠性增长，忽略了其实际使用可靠性的区域差异规律对保修期的影响。

目前，国内外分析产品使用可靠性与区域差异的关联性及应用于制定相关产品保修期的研究极其有限，仅有Jie等[4]从工作环境和用户使用习惯两个维度，系统研究了空调使用可靠性影响因素的区域差异性。揭丽琳等[29]在文献[4]的基础上，以产品使用可靠性同类区域差异最小为目标，建立了使用可靠性基于工作环境和用户使用习惯两类因素的多变量高维聚类模型，并运用智能聚类算法有效地解决了产品使用可靠性的区域粒度划分问题。刘卫东等[30]利用部分省域的售后故障数据统计分析计算空调产品的实际使用失效率，并定量分析不同区域的保修期差异程度，但保修期求解模型仅考虑了使用失效率和保修成本两个有限因素，既没有考虑保修期与价格的相互关系，也未能建立产品使用可靠性与所处地理区域间的定量关系模型，因而无法定量确定其他大部分区域的保修期。而已有研究表明，产品价格与保修期、产品可靠性及保修成本等因素密切关联[31-32]。因此，从使用可靠性区域差异角度优化设计保修期，仍需深入研究。

然而，精准预测出产品使用可靠性是实现基于使用可靠性的保修期优化决策的制约因素。笔者前期对使用可靠性影响因素及其区域粒度划分开展了深入分析和探讨[4,29]。在此基础上，本文将根据使用可靠性的区域粒度划分结果，并结合售后故障数据的统计分析构建使用可靠性预测模型；研究建立综合考虑使用可靠性区域差异、保修成本和价格的保修期优化决策模型，从而使得定量揭示使用可靠性区域差异对产品保修期和价格的影响规律成为可能。

针对以上分析，本文首先建立了反映产品使用可靠性与不同区域间定量关系的数学模型，并应用于预测分布在不同区域的产品使用可靠性水平；然后构建了基于使用可靠性区域粒度的保修期优化决策模型，推导证明该模型存在最优解，并给出模型的求解方法。最后，以某具体型号空调产品的保修期决策为实证案例，深入阐述了基于使用可靠性的保修期优化决策的具体实施过程，从而验证了模型的有效性和适用性。

1 保修期优化决策分析

进行产品保修期优化设计时，要综合考虑产品可靠性、目标市场的销售价格以及企业的保修成本投入等各种决策的相互作用。因此，在建立产品保修期优化决策模型之前，首先需要重点分析和提取影响企业制定保修期的关键因素。

1.1 保修期决策框图模型的构建

可靠性是工程技术策略的核心因素。基于可靠性的角度，若产品的固有可靠性水平越高，则可制定越长的保修期。固有可靠性主要受产品研发、生产阶段的原材料控制、质量控制和劳动力技术水平等诸多因素的影响，而使用可靠性是产品在实际使用环境中所具有的可靠性。产品的固有可靠性是其使用可靠性的基础，且固有可靠性对使用可靠性具有正面效应，即使用可靠性随固有可靠性的增长而增长。鉴于售后服务标准化程度的日益提升，使得其对使用可靠性的影响日趋一致，故在此不考虑产品安装等服务质量因素的影响。但是分布于不同地理区域的产品，由于所处自然环境、用户经济条件、生活习惯等因素的不同，使得其实际使用可靠性呈现显著的区域差异性。此外，产品使用可靠性水平的差异必然会影响到保修期的长短和保修成本的高低。因此，要以使用可靠性为基础进行产品保修期优化设计，首先要完成的就是使用可靠性区域差异的评估，而这也为实现保修期决策的优化奠定了基础。

另一方面，不同保修期下所产生的保修成本、销售价格和销售量也各有差异。一般而言，消费者可以依据保修期对产品感知质量进行判断，从而影响顾客的消费选择，进而影响产品的销售量和销售价格。与此同时，销售价格是市场及决策中唯一能创造利润的因素，但要受企业所处的竞争地位、行业竞争态势等市场环境因素的制约。此外，销售价格会反向作用于产品销售量，即销售量随价格的增加而减少，同时它又受市场环境以及各区域的消费者需求差异等因素的约束。综合上述分析，可建立如图1所示的基于使用可靠性区域粒度的保修期决策框图模型。

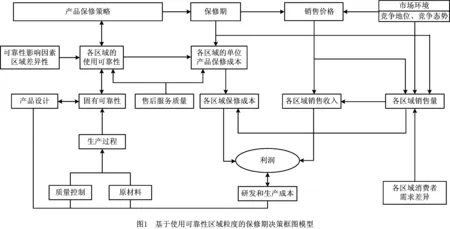
该决策模型综合考虑工程技术策略、市场策略以及使用可靠性区域差异3个方面的影响，通过分析保修期、各区域保修成本、研发和生产成本、销售价格、各区域销售量、各区域销售收入以及企业利润之间的相互影响及作用，并以利润最大化为企业的经营战略目标，优化选择最优的产品保修期与价格。

1.2 使用可靠性预测模型的构建

对于多批次大批量生产的产品，其同型不同代产品的功能与结构基本保持稳定，即工作环境和用户使用习惯等因素对同型各代产品的可靠性的影响程度基本一致。基于此，可以充分利用企业以往掌握的同型各代产品的使用可靠性数据，从而定量分析计算两类因素对产品可靠性的综合影响程度，进而准确地预测出分布在不同区域的新一代产品的实际使用可靠性。

1.2.1 使用可靠性与区域间定量关系模型的构建

准确评估不同类型区域的产品使用可靠性水平和可靠性影响因子是构建保修期优化决策模型的重要前提。由于前期研究[29]中确定的使用可靠性区域粒度划分能够充分反映各类地理区域内可靠性影响因素及其影响程度的一致性，并精准地实现了同类区域产品使用可靠性水平差异尽可能小，以及不同区域产品使用可靠性水平差异尽可能大，且其本质是根据区域聚类样本间的距离进行度量的。为此，可以采用各类区域间距离的远近来表征产品实际使用可靠性的区域差异程度。

|Δλij|=|λi-λj|=δDij+ξ,

Dij=ω1·dij(AQED)+ω2·dij(ISED)+

ω3·dij(VCED)。

(1)

式中：λi、λj分别表示第i类和第j类区域同型产品的使用失效率，用于表征产品实际使用可靠性水平；Δλij则表示第i类和第j类区域的产品失效率差，即两类区域使用可靠性的差异程度；δ、ξ为待定系数；Dij表示第i类和第j类区域之间的综合距离；dij(AQED)、dij(ISED)和dij(VCED)分别表示绝对量距离，增速距离和波动距离；；ω1、ω2、ω3分别表示3种距离相应的权重系数，且满足ω1+ω2+ω3=1，各距离及权重的计算详见前期研究[4]。

1.2.2 使用可靠性及影响因子的评估

为了预测不同区域的产品使用可靠性水平，必须先确定上述产品使用可靠性与不同区域间距离的函数关系式，下面给出具体求解步骤：

(2)

(2)其次，结合前期研究得到的使用可靠性最优区域粒度划分方案，按照式(1)可分析计算得到各类区域间的距离。

(4)最后，通过计算可靠性影响因子来度量不同区域同型产品的使用可靠性差异程度，即

(3)

2 基于使用可靠性区域粒度的保修期优化决策模型

2.1 模型建立

文献[26-27]认为产品的保修期与价格都会影响产品需求量，且将其看作是保修期长度和单位售价指数形式的对数线性函数。在此基础上，本文将全国地理区域按产品使用可靠性水平的高低进行了粒度划分，则不同区域的产品销售量可表示为：

Qi(P,WX)=ki(WX+τ)βP-γki，τ>0;1≤i≤c。

(4)

式中：c为产品使用可靠性区域粒度划分数目；ki(ki>0)为尺度参数，表征第i类区域的市场竞争、潜在消费者数量和消费者购买力以及需求差异等因素的综合影响；Qi(P,WX)表示第i类区域的产品销售量，不再是以往的适用于所有区域的统一固定常数值，而是随不同区域市场环境变动而变化的函数；WX为产品保修期；τ为时间位移常数，以保证当WX=0时，产品销售量非零；P表示产品的销售价格；β(0<β<1)为销售量关于保修期的偏移弹性系数；γ(γ>1)为产品的销售量关于价格的弹性系数。由式(4)可知，价格对销售量具有负面效应，即销售量随价格的上涨而下降；而保修期对销售量具有正面效应，即销售量随保修期长度的增加而增长。

为建立保修期优化决策模型，作出以下假设：企业采用免费更换保修策略，承担产品保修期间发生维修或更换的全部成本，包括运输成本、管理成本、材料成本和劳动力成本等，这些费用合计为单次故障平均维修成本；第i类区域的单位产品在保修期内发生故障的次数与该区域的单位产品在保修期内第j次故障的保修成本是相互独立的变量；并且产品在保修期内故障次数呈指数分布。

对于分布于第i类区域的单位产品，其保修成本由保修期内各次故障的维修成本之和决定，即

0≤t≤WX;

1≤i≤c。

(5)

式中：Yi(WX)为第i类区域的单位产品在保修期内发生故障的次数；Xij(t)为该区域的单位产品在保修期内第j次故障的保修成本。由于Xij(t)与Yi(WX)是相互独立变量，则第i类区域的单位产品的期望保修成本为

ω(WX,λi)=E[Zi(WX)]=

E[Xij(t)]E[Yi(WX)]。

(6)

假设单位产品在保修期内单次故障的平均维修成本为cm，则第i类区域单位产品的期望保修成本为

ω(WX,λi)=cmλiWX。

(7)

综合上述，考虑企业的经营战略目标是总利润最大化，其总利润由产品价格P、销售量Qi(i=1,2,…,c)、单位研发成本cr、单位生产成本cp、期望的保修成本ωi(i=1,2,…,c)共同决定，若产品使用可靠性区域粒度可划分为c类，则其保修期优化决策模型可表示为

(8)

s.t.

WX∈[0,Lmax]，

P∈(Camin,Pcmax)，

1≤i≤c。

(9)

式中：πX为企业的综合总利润水平，Lmax为当前产品的最大安全使用年限，Camin为单位产品的最小平均成本，Pcmax为消费者可接受的最高价格，Cwmax为企业在保修期内预计支出的总售后维修成本，其中Pcmax和Cwmax可在新产品投放市场前通过市场调研与利润分析确定。

2.2 模型求解

首先由式(8)可以得出，企业利润函数关于P和WX的黑塞矩阵，即

式中：

(P-cr-cp-cmαiλ0WX)+2cmαiλ0(WX+τ)]，

(10)

[βP+γcmαiλ0(WX+τ)-βγ(P-cr-

cp-cmαiλ0WX)]，

(11)

cp+cmαiλ0WX)-γ(P-cr-cp-cmαiλ0WX)]。

(12)

设D1和D2分别是一阶和二阶主子式，则

(13)

(14)

通过对式(8)分别求关于WX和P的一阶偏导数，并令其各自为零，得到如下方程：

cp-cmαiλ0WX)ki(WX+τ)β-1P-γ]=0，

(15)

cp-cmαiλ0WX)ki(WX+τ)βP-γ-1]=0。

(16)

(17)

(18)

(19)

3 模型应用

下面将所提模型应用于中国某空调企业的保修期优化决策分析，验证所建模型的有效性和适用性。在此基础上，获得某一具体型号的空调产品的使用可靠性以及最优保修期和价格的组合策略，并对保修期优化决策模型的保修期偏移弹性系数、价格弹性系数的灵敏性进行详细分析和讨论。

3.1 应用研究背景与数据来源

根据前期研究[29]得到的空调使用可靠性区域粒度划分结果设置c=10，ki(i=1,2,…,c)则是先由《中国区域经济统计年鉴》[31]中空调拥有量数据确定出不同区域的空调销售量Qi，再由当前空调企业普遍采用的保修期及平均销售价格经式(4)反求计算得出即ki=Qi(P,W)(W+τ)-βPγ，依此类推得到如表1所示的取值。

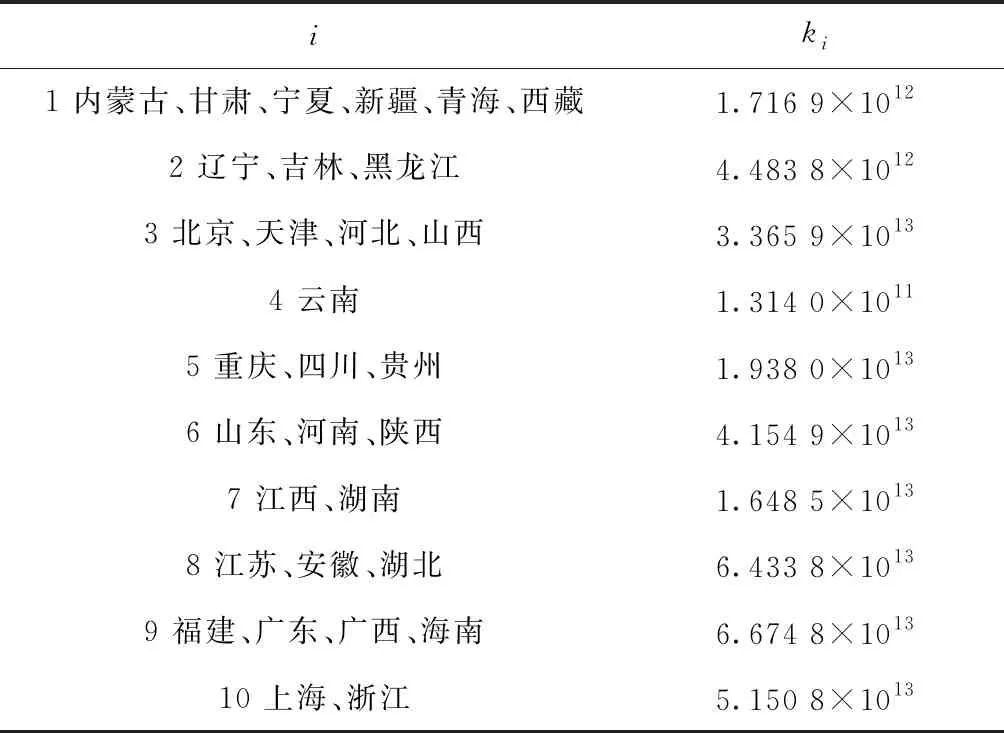
表1 不同类型区域的ki参数取值

现根据某型空调可靠性数据得出该同型产品的固有失效率λ0为0.008 03次/年，设研发成本cr为500元，生产成本cp为1 100元，单次故障的平均保修成本cm为400元，Lmax为12年，Camin为2 000元，Pcmax为4 000元。根据我国空调拥有量的实际情况以及相关文献[26-27]的数据，设置销售量参数分别为β=0.02，γ=2，τ=0.5，保修期内预计支出的售后维修成本上限Cwmax为100 000 万元。

3.2 保修期优化结果与分析

现根据某型空调可靠性数据得出该同型产品在部分区域的使用失效率，并根据式(1)计算得到的区域距离，利用最小二乘法可得到δ=0.001 8，ξ=-0.002 4，即空调使用失效率与不同区域距离间的关系模型可表示为

|Δλij|=|λi-λj|=0.001 8Dij-0.002 4。

由此可得不同类型区域的空调实际使用失效率λi和可靠性影响因子αi，如表2所示。由表2可知，分布于不同区域的空调产品，其实际使用失效率存在较明显区域差异，并且可靠性影响因子越大，表明该区域的空调可靠性水平受影响的程度越大，则实际使用失效率就越高。

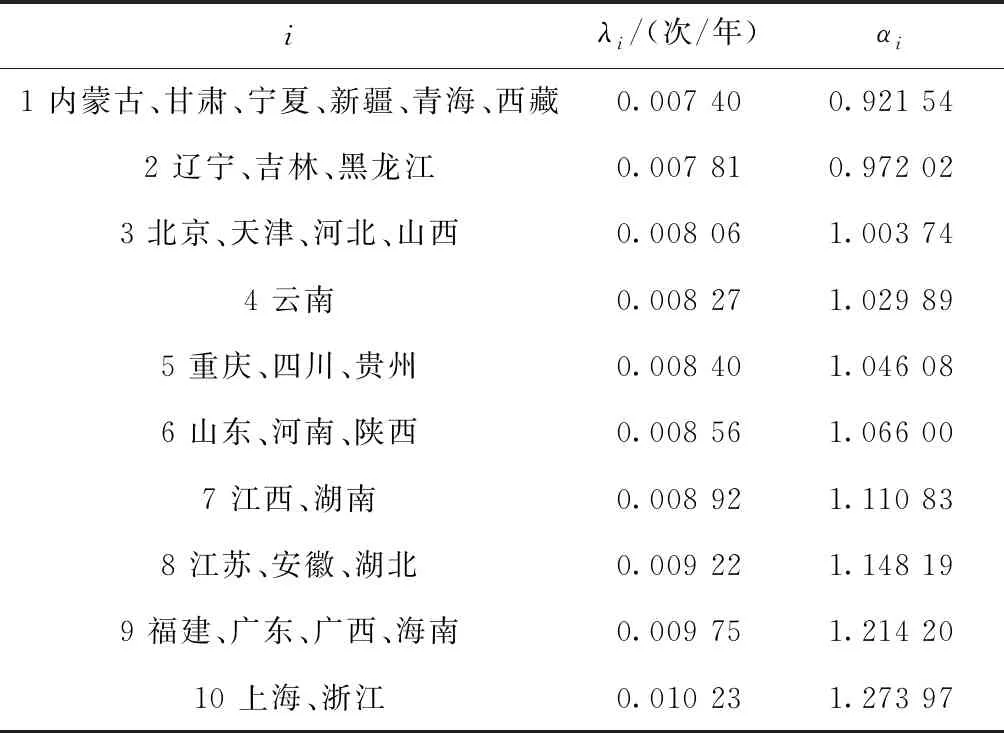
表2 不同类型区域的空调使用失效率和可靠性影响因子

将所得参数值带入式(17)和式(18)，进一步求出空调最优保修期和价格的组合策略，并与固有可靠性以及文献[20]提出的基于固有可靠性增长的保修期优化进行比较，具体结果如表3所示。表中，“—”表示目标函数未考虑该决策变量。

表3 三种保修期求解模型的结果比较

由表3可知，本文提出的基于使用可靠性区域粒度的保修期优化决策模型所得的保修期有较大程度的延长，而固有可靠性增长次之，固有可靠性最短，造成其结果差异的根本原因是基于固有可靠性的保修期研究中假设不同区域的空调使用可靠性水平均等同于出厂时的固有可靠性。此外，文献[20]仅以保修期为决策变量构建单位产品的保修利益预测函数，因此不能求解得到相应的产品价格。而本文所提模型综合考虑了产品价格、使用可靠性区域差异和保修期因素的影响，实现了三者的联合优化。因此，根据产品的使用失效率，空调企业能够科学地制定更符合客观实际的保修期。

3.3 灵敏性分析

3.3.1 保修期偏移弹性系数的灵敏性分析

为进一步分析模型的保修期偏移弹性系数β的变化对保修期、产品价格、各区域的保修成本、各区域销售量以及各区域企业利润分布的影响，在其他参数保持不变的条件下，设置β的5组不同取值，分别采用β=0.010,0.015,0.020,0.025,0.030这组逐渐递增的参数值进行仿真实验，表4记录了在不同参数取值下的实验结果。保修期偏移弹性系数β的变化对各类区域单位产品保修成本的影响，如图2所示。不同β下的各区域销售量和各区域企业利润分布结果，如表5和表6所示。

表4 不同β下的最优价格和保修期组合策略

表5 不同β下的各区域销售量(台)分布结果

续表5

同时由表5可以看出，保修期长度的增加又促进消费者购买的作用，从而使各类区域销售量也随β的增大而呈现不同比例的增加；当β由0.010增加到0.030时，各类区域i∈[1,10]的销售量增加了约2.5%。由表6可以看出，由于各区域价格、销售量的增加，使得企业在各区域的盈利随着β的增大而不断提高；通过表中数据比较分析表明，无论β取何参数值，企业在i=3,6,8,9,10五类区域的盈利是较多的。因此，企业应尽量满足这些类型区域的消费者，适度延长产品的保修期，增加产品销售量，从而达到增加企业总利润的效果。

表6 不同β下的各区域企业利润(元)分布结果

续表6

3.3.2 价格弹性系数的灵敏性分析

为进一步研究模型的价格弹性系数γ的变化对保修期、产品价格、保修成本、销售量以及企业利润产生的影响，同样固定其他参数不变，设置γ的6组不同取值，分别采用γ=1.7,1.8，1.9,2.0，2.1,2.2,2.3这组逐渐递增的参数值进行仿真实验。不同参数取值下求得的空调最优保修期、价格和企业利润，如表7所示。价格弹性系数γ的变化对各类区域单位产品保修成本、销售量以及企业利润分布的影响，分别如图3～图5所示。

表7 不同γ下的最优保修期和价格组合策略

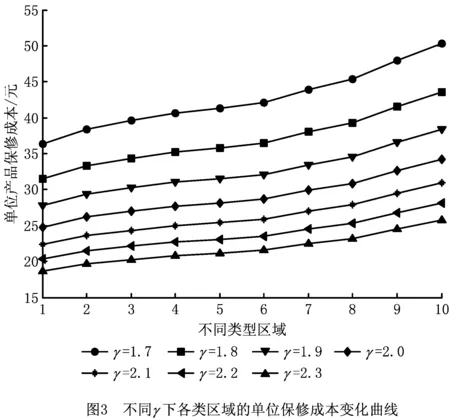
从图4可知，保修期长度的减小同时又使各类区域销售量减少，因此各类区域销售量随γ的增大而单调递减，且下降的幅度在逐渐减小；图4数据还表明，当γ由1.7增加到2.3时，各类区域i∈[1,10]的销售量总体下降了约98%。由图5可以看出，由于各区域价格、销售量的减少，企业在各类区域分布的利润随着γ的增大而不断减少，且减少的幅度呈现先大后小的趋势；分析结果还表明企业利润主要集中在i=3,6,8,9,10这5类区域，这与表6分析得出的各区域利润分布规律相吻合。

4 结束语

本文针对产品保修期设计的优化问题，在系统分析保修期的关键影响因素的基础上，根据使用可靠性的区域粒度划分结果，建立了反映产品使用可靠性与不同区域间定量关系的数学模型，并应用于预测分布在不同区域的产品使用可靠性水平；并由此构建了基于使用可靠性区域粒度的保修期优化决策模型，推导证明了该模型存在最优解，并给出了模型的求解方法。最后，运用所建模型对空调产品实例进行使用可靠性评估和保修期优化决策，并与传统方法对比，验证了模型的有效性和适用性。

使用可靠性预测模型能够精确评估不同区域的使用可靠水平，最大限度地挖掘了使用可靠性的区域差异规律蕴含的效益；保修期优化决策模型综合考虑了产品使用可靠性的区域差异性、保修成本和价格因素的影响，有利于联合优化使用可靠性、保修期和价格，从而使得制定的保修期更符合客观实际。研究结果表明，基于使用可靠性的视角，适度增加保修期长度有利于实现企业利润最大化；通过模型参数的灵敏度分析，定量揭示了保修期偏移弹性系数和价格弹性系数对空调保修期、价格以及企业利润的影响规律。不同于一般的产品保修期决策方法，本文建立的模型增加了使用可靠性区域差异视角，既为解决空调保修期优化设计问题提供了一种新思路，也为企业制定科学合理的保修期提供理论指导和技术支持。

然而，本文所构建的保修期优化决策模型仍存在一些局限性，如，由于数据获取的困难性和可得性，没有对渠道投入、广告投入和品牌影响力等影响因素进行定量分析。未来将进一步探讨和改善该模型，并将其推广应用于其他类型家电产品保修期设计的优化问题。