基于车道等饱和度的交叉口车道功能优化模型
聂 磊,马万经
(同济大学道路与交通工程教育部重点实验室,上海201804)
车道功能划分是根据交叉口进口车道车流模式将车道与交通流进行匹配[1]。车道功能划分是交通设计的重要内容,其合理性直接关系到交叉口空间资源利用和运行效率[2-5]。
车道功能分专用车道和合用车道两种。其中,合用车道是交叉口车道功能设置的常用形式,常规合用(共享)车道是指直行、左转及右转三者之间共用或合用一条车道,包括直行左转合用车道、直行右转合用车道、直行与左右转合用车道及左右转合用车道等[6]。以往许多研究更多关注独立的左转、直行和右转车道功能[7-10],对合用车道功能布置研究较少,往往侧重于研究合用车道通行能力、饱和流量等[11-12]。另外,许多研究[13-15]将合用车道构成车道组,作为一个整体进行研究,忽略不同合用车道功能会导致车道流量不均衡分布,车道饱和度无法做到均衡,影响交叉口通行效率,甚至得出错误结论。
传统的交叉口机动车道功能划分[7,16-17]主要考虑道路几何条件、交通流量情况,根据经验提出左转、右转车道设置条件,或提出某一试算方案,缺乏理论和模型的指导。
Wong等[18-20]建立了基于车道的逻辑变量反映每个车道是否能够允许通行到各出口方向,每个进口车道功能变量数等于交叉口进口数乘以进口车道数,变量数较多,而且变量与进口车道数量直接相关,模型通用性不够。白玉[7]和王京元等[8]以流向的车道数建立了车道功能矩阵,更适用于独立功能车道布置,但对合用车道的表达不很直观。张鹏等[9]、马万经等[10]提出基于 Ring-Barrier[15]相位的车道功能向量模型,但车道功能模型做了简化,没有考虑直右、直左右、左右等合用车道,应用受限。赵靖等[2-4,21]提出了动态车道及出口道左转的车道功能优化模型,但没有考虑出口道的优化。
基于以上分析,本文建立基于车道等饱和度的交叉口车道功能优化模型,模型以交叉口流量、各进出口和路段车道数为输入,以进口流量比最小和进口流量比方差最小为目标函数,构建约束条件保证各车道功能齐备、流量与车道功能匹配、合用车道均衡饱和度、进出口道车道数平衡。然后,通过LU分解和枚举算法,能够一次生成所有可行的车道功能划分方案并进行优化。最后,实例验证表明,交叉口车道功能优化模型有效。
1 车道功能优化模型
1.1 模型输入
(1)交叉口流量:Qi,j,i,j∈ {1,2,3,…,N},i,j代表方向或进口序号,南进口为1,序号顺时针增加,N为交叉口进口数。
(2)交叉口第i个进出口总车道数:Li。
(3)交叉口第i个进口路段车道数:Bi。
1.2 模型变量
δi,k为第i个进口第k种车道功能的车道数,k={0,1,2,…,7},共计N×8个变量,若N=4,则有32个整数变量。8种车道功能中k=0代表出口道,k=1~7分别代表左转(掉头或左转掉头)、直左车道、直行车道、直左右车道、左右车道、直右车道、右转车道,如图1所示。
1.3 模型约束
1.3.1 进出口道数量约束
第i个进口的进口道车道数和出口车道数之和等于总车道数,第i个进口第k种车道功能的车道数大于等于0,出口道数不小于路段基本车道数,不大于出口车道数+1。

1.3.2 合用车道约束
合用车道的数量至多一条,否则进口内部车道就将产生冲突。若有直左右车道,则直行、直左、左右、直右车道数量均为0,否则将产生冲突。

若δi,4=1,则δi,2= δi,3= δi,5= δi,6=0,即

若δi,5=1,则δi,2= δi,3= δi,4= δi,6=0,即

1.3.3 车道功能模式
进口车道数:Mi=Li-δi,0,根据车道功能不同,进口车道功能一般可以分为4种模式,模式I为独立的左转、直行和右转车道,进口道为3组独立的车流(车道组);模式II为具有直左合用车道,没有直右合用车道;模式III为有直右合用车道,没有直左合用车道;模式IV为有直左右合用车道或同时具有直右和直左车道,整个进口道为一个车道。
模式I的方案组合数可以表达为左转车道数分别为1,2,3,…,Mi条情况下的直行和右转专用车道功能方案组合数之和。同理,模式II的组合数可以表达为直左合用车道在左侧开始第1车道、第2车道、…、第Mi车道情况下同时有直行和右转专用车道方案和全部为右转专用车道方案组合数之和。模式III和模式II类似,组合数相同。模式IV-1的组合数为Mi。模式IV-2的组合数可以表达为直行车道数为0、1、2、…、Mi-2条情况下同时有左转右转专用车道方案、只有左转和只有右转的方案组合数之和。4种模式的组合数和模型表达如表1所示。
进口车道功能组合数量随着进口车道数呈现抛物线增长。若出口道数也是可变的,则进口道车道功能组合将成倍增加。如图2所示。
1.3.4 流量与车道功能匹配
若某个流向流量大于0,则必须有该流向的车道功能。同理,若某个流向流量等于0,则禁止该流向的车道功能。


表1 进口道车道模式Tab.1 Approach lane function pattern

图2 进口车道数与车道功能组合关系Fig.2 Approach lane count and lane function count

式(7)、(8)中:Qi,(i+1)modN为左转流量;Qi,(i+2)modN为直行流量;Qi,(i+3)modN为右转流量。mod运算为除法运算后的余数。
1.3.5 车道组流量等饱和度
对于模式Ⅰ,左转、直行和右转都是独立车道,各流向的车道流量都是平均分配,每种车道功能的每个车道的流量比和饱和度都是相同的。而对于模式Ⅱ~Ⅳ,合用车道与多个车道共同构成车道组,如果按照车道组整体进行优化,默认车道组内所有车道流量均衡分配,完全共享,按等饱和度原则分配车道流量是偏乐观和理想的。有些车道功能方案设置了合用车道,但实际车道流量无法完全共享做到等饱和度,所以采用将车道作为优化对象更符合实际。对于存在直行左转合用车道的模式Ⅱ和直行右转合用车道的模式Ⅲ,同样存在上述问题。如果这些方案合用车道流量不均衡,无法做到等饱和度或等流量比,从本质上来讲应转化为模式Ⅰ,所以,这些不合理的车道功能方案应予以舍弃。
(1)模式Ⅱ
直行和左转合用车道构成一个车道组,根据排队理论,车道组内部车道的饱和度相同,由于车道组在信号控制中是共用一个信号灯组,绿灯时间也相同,所以车道组内部车道的流量比也应相同。即
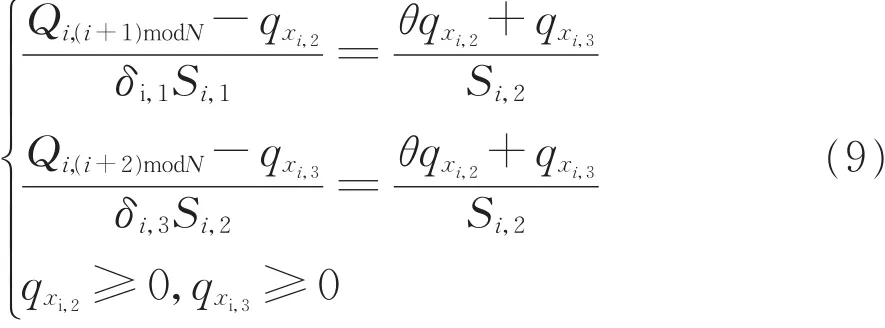
式中:qxi,2和qxi,3为i进口直左合用车道中的左转和直行流量;Si,1=1 650 pcu.h-1、Si,2=1 800 pcu.h-1和Si,3=1 550 pcu.h-1分别为左转、直行和右转饱和流量[13];θ为左转流量对直行流量折算系数θi=Si,2/Si,1,有
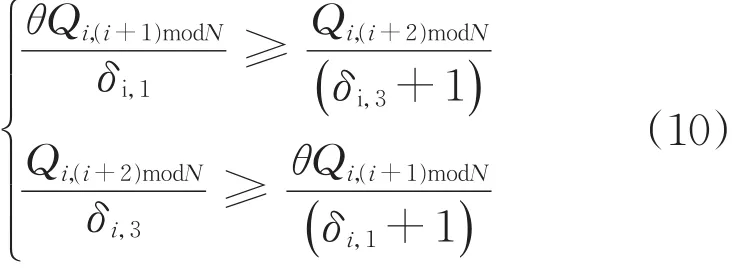
若满足约束(10),则左转和直行合用车道流量为 (Qi,(i+1)modN+Qi,(i+2)modN)/(δi,1+δi,3),右转单车道流量为Qi,(i+3)modN/δi,7,否则无法做到车道组内车道等饱和度,在这种条件下采用合用车道模式不合理,车道功能应该调整为模式Ⅰ。
(2)模式Ⅲ
等饱和约束条件为

式 中 :φ=Si,2/Si,3为 右 转 流 量 对 直 行 流 量 折 算系数。
若满足约束(11),则左转流量为Qi,(i+1)mod4/δi,1,直行和右转合用车道流量为 (Qi,(i+2)mod4+Qi,(i+3)mod4)/,否则车道布置不合理。
(3)模式Ⅳ-1
等饱和约束条件为

Si,0=min(Si,SL,Si,SR),Si,SL为直行左转合用车道饱和流量,Si,SR为直行右转合用车道饱和流量。
(4)模式IV-2
等饱和约束条件,分为8种情况。
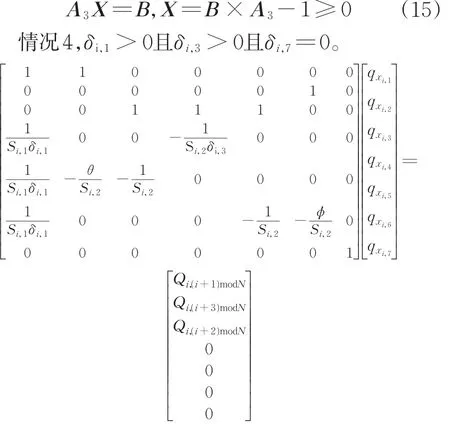
情况1,δi,1> 0且δi,3> 0且δi,7> 0为保证进口各车道的流量守恒和车道等饱和度,可表达为如下方程组:

化简后可表达为矩阵形式为


即

同理可以得到情况2~8的约束,如下。
情况2,δi,1=0且δi,3> 0且δi,7> 0 。

即

即
即

即

即

即

即

上述方程为线性方程组,可以采用LU分解法求解。如果矩阵A的秩和增广矩阵[A B]的秩相同,且都是7,则线性方程组有唯一解;若其秩相等但小于7,则线性方程组有无穷解;如果矩阵A的秩与增广矩阵[A B]的秩不相同,则无解。只有当解X的所有元素都不小于0,才是可行解。
因上述模型是线性方程组,若交叉口流量同比例增长,则各车道的流量也同比例增加,流量比也是同比例增加。
1.3.6 交叉口进出口道车道平衡
一般情况下,出口道车道数要大于等于左侧右转车道、对向直行车道和右侧左转车道的车道数。
左侧右转车道,满足

对向直行车道,满足
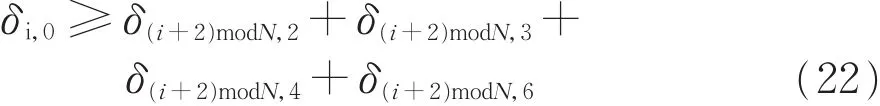
右侧左转车道,满足

1.3.7 左转专用车道约束
根据HCM2000手册,有
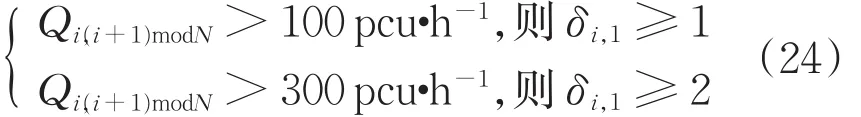
该约束选择性使用,若车道数较多,则开启,可大幅度减少计算量;若车道数不多,建议可不采用该约束,尽量得到全局最优解。
1.4 目标函数
流量比是可以充分反映交叉口时空资源的重要参数,对于模式Ⅱ、Ⅳ-1和Ⅳ-2,相位方案一般选择单口放行,可选择进口流量比最小为目标函数优化进口车道功能方案。

式中:l为进口车道序号
对于模式Ⅱ,直左车道和直行车道流量比相同,对于Ⅳ-1和Ⅳ-2整个进口各车道流量比相同。
对于模式Ⅰ和Ⅲ,可采用的相位方案较多,严格意义上需要结合相位和信号配时进行交叉口整体优化,本文予以简化,以进口车道的流量比方差最小为优化目标。

1.5 模型算法
由于单个进口车道数一般不超过10条,其所有车道功能方案有限,所以可以采用枚举法进行求解。
1.5.1 生成进口所有可能车道功能方案
根据输入和约束(1)~(6),生成各进口道的可能车道功能。
1.5.2 筛选满足流量匹配、出口车道约束方案
根据约束(7)~(8)、(21)~(23),筛选满足流量匹配和出口车道约束的所有方案。
1.5.3 筛选满足车道等饱和约束的方案
(1)选择某一个车道功能方案。
(2)根据车道方案的模式,采用车道等饱和度约束,判断是否选入备选方案。
①若为模式Ⅰ,选为备选方案,返回(1)。
②若为模式Ⅱ,满足约束(9)~(10),选为备选方案,否则返回(1)。
③若为模式Ⅲ,满足约束(11),选为备选方案,否则返回(1)。
④若模式为Ⅳ-1,满足约束(12),选为备选方案,否则,返回(1)。
⑤若模式为Ⅳ-2,根据8种情况和约束(13)~(20),采用LU分解法求解各车道分配流量,若流量均为为非负,则选为备选方案,否则返回(1)。
(3)所有车道功能方案枚举结束,生成所有等饱和的车道功能可行方案。
1.5.4 针对不同车道功能模式,选择不同目标函数
(1)将模式为Ⅱ、Ⅳ-1和Ⅳ-2的方案归并为集合F24,模式Ⅰ和Ⅲ为一个集合F13。
(2)计算方案集合F24进口各车道流量比,各车道流量比的最大值作为进口流量比。
(3)集合F24流量比最小值对应的方案为模式Ⅱ、Ⅳ-1和Ⅳ-2对应的最优方案。
(4)计算方案集合F13进口车道流量比方差,并选出最小值对应的方案为模式Ⅰ和Ⅲ对应过的最优方案。
2 模型验证与分析
2.1 交叉口基本参数
本文以张家港的人民路-长安路四叉十字路口为案例,如图3所示。各路口均是进口4条车道,出口3条车道。信号相位为对称放行4相位。
交叉口高峰小时流量见表2。

图3 交叉口交通设计图Fig.3 Layout of intersection and signal groups
2.2 车道功能方案优化
2.2.1 车道功能生成
以南进口为例,4条车道,根据公式计算,总共25种可能的车道功能布置方案,具体如表3所示。

表2 交叉口流量表Tab.2 Traffic demand
经出口道和合用车道等饱和约束验算,3个方案不满足出口车道约束,13个方案不满足等饱和约束,9个方案是可行方案,其中模式Ⅰ有3个,模式Ⅱ有3个,模式Ⅲ有3个,流量比(按照左转、直行、右转的顺序)和目标函数值如表4所示。

表3 南进口所有车道功能方案表Tab.3 All lane function of southern arm
由表4可知,方案1~3属于模式Ⅱ,根据式(25)可得方案3为最优;方案4~9属于模式Ⅰ和Ⅲ,根据式(26)可得方案7为最优。同理,分别计算另外三个进口最优车道布置方案,综合得到交叉口推荐方案如表5所示。
2.2.2 交叉口车道功能优化
每个进口有2个方案,4个进口组合有16个方案,但考虑到进口选择模式Ⅳ和Ⅴ,则对向进口选择模式Ⅳ和Ⅴ更优,东西进口只能采用E1-W1和E2-W2,方案减少为8组,按照单口放行及Dural-Ring相位方案,以交叉口关键流量比最小为目标,计算结果如图5。
2.2.3 结果分析
8组方案,交叉口最小流量比之和为0.888~1.051,模式Ⅳ整体合用车道的E2-W2方案普遍优于专用左转的E1-W1方案。因S2方案为模式Ⅱ而不是模式Ⅳ,其结果均劣于S1。
根据图4的原车道功能方案,其关键流量比之和为1.062,最优方案的关键流量比之和为0.888,减少了16.4%,效益提升明显。

表4 南进口车道功能可行方案Tab.4 Feasible lane function of southern arm

表5 交叉口各进口最优车道功能方案表Tab.5 Optimal Lane function of all arms

图5 交叉口关键流量比Fig.5 Critical flow factor of intersection
经优化,交叉口最优车道功能方案为S1-N2-E2-W2,车道功能布置如图6所示。
经计算验证,交叉口流量按等比例增加或减小,其最优车道功能方案保持不变,流量比呈现等比例线形调整。如图7所示。

图6 交叉口最优车道功能布置Fig.6 Optimal lane allocation plan of intersection

图7 交叉口流量与关键流量比的变化Fig.7 Flow and versus critical flow factor at intersection
3 结论
(1)本文建立了交叉口车道功能优化模型,模型考虑进出口道车道平衡、车道功能不冲突、车道等饱和度等约束,目标函数根据不同车道模式采用进口流量比最小和进口流量比方差最小。
(2)经实例验证,交叉口车道功能优化模型简单有效,能够给出每个进口推荐备选车道功能方案。模型可以较大程度降低交叉口关键流量比之和,提高交叉口交通设计的效率和精度。
(3)以整个交叉口关键流量比最小为目标,模式4因车道整体合用其流量比最小,效率更高更具优势,但其相位方案只能单口放行,对行人和非机动车通行不利。因此,下阶段还需将行人、非机动车通行因素纳入模型一并考虑。

