大型三面广告牌结构风荷载特性的风洞试验

汪大海，向 越，罗 烈，李志豪，彭勇波，申 琪

（1.武汉理工大学土木工程与建筑学院，湖北武汉430070；2.同济大学土木工程学院上海200092）

近年来，大型单立柱户外广告牌作为我国户外广告设施的主要形式，已广泛建造于市区、高速公路以及铁路等周边。常见的广告牌形式有双面和三面两种，高度通常在15～50 m之间，主要受力构件为钢管支撑柱、型钢及桁架支架，面板为镀锌钢板。独特的结构形式易使这类广告牌结构遭受风灾的破坏，由于其往往位于交通要冲，一旦破坏所造成的人员伤亡及财产损失影响较大，已成为一种典型的城市风灾易损性结构。主要破坏模式包括：极值风压造成的广告牌面板蒙皮及骨架的破坏；风力造成的面板支撑框架的破坏，以及风振作用下立柱破坏引起的整体倒塌［5］。

已有的国内外户外广告牌结构风荷载特性研究对象主要为单面自立式广告牌。Letchford等［1-2］通过风洞试验得出不同高宽比、间隙率和遮挡等的单板广告牌的阻力和表面法向风压系数，并被多个国家规范的抗风设计所采纳［3-4］。近年来，宋芳芳等［5］开展了广告牌风灾调查研究。Smith等［6］通过不同间隙率、高宽比的风洞试验考察了双面箱型LED广告牌整体阻力与扭矩系数分布规律。顾明等［7］进行了双面和三面广告牌风压分布特性的风洞试验研究。Wang等［8-10］开展了大型双、三面广告牌面板风荷载特性的试验研究并深入讨论了双面广告牌面板局部风压的非高斯特性。目前，针对大型单立柱广告牌这类特殊开敞的板式结构，尚缺乏面板净风压特性、体型系数和结构整体风力系数分布规律的全面掌握，其取值直接关系到广告牌结构面板连接、面板水平支撑体系和立柱的结构设计与抗风性能。

鉴于此，本文以国家建筑标准设计图集［11］中的三面广告牌为原型，制作刚性测压实验模型。通过对广告牌模型进行风洞试验，测定广告牌模型的面板表面风压，研究净风压系数及面板风力系数在各类影响因素下的变化及分布规律；根据部分风向角下沿面板长方向的平均压力分布，给出其近似简化结果；给出了结构整体风力系数随风向角的变化规律。研究为三面广告牌上部结构面板与支撑骨架风荷载设计改进提供了试验数据与计算依据。

1 风洞试验

1.1 模型参数及测点布置

试验原型采用标准图集［11］中典型三面独立柱广告牌结构，尺寸如图1a所示，选用面板实际尺寸为6 m×18 m，高度为21 m。三面广告牌模型试验风向角如图1b所示，三个面板呈中心对称布置，面板间夹角θ为60°，测压模型几何缩尺比为1：20。试验采用松木薄盒模拟面板的正反两面，内外面板的测压管均布置在薄盒内部，避免了对板内侧的压力测量造成干扰，如图2所示。6个面上测压孔的位置保持一致。参照文献［7］中类似的广告牌结构试验，考虑到风压分布在气流分离处的变化，测点布置采取边密中疏、满布对称的方式，单侧面板表面布置84个测点，总测点数为84×6=506个，如图3所示。

图1 三面广告牌原型Fig.1 Prototype of three-plate billboard

1.2 风洞及风场模拟

图2 三面广告牌模型Fig.2 Model of a three-plate billboard

图3 三面广告牌模型测点布置（单位：mm）Fig.3 Locations of pressure taps of the modsl of the three-plate billboard

刚性广告牌模型的测压试验在同济大学土木工程防灾国家重点实验室TJ-3大气边界层风洞中进行。实际中，广告牌一般位于较为空旷的郊区或者公路、铁路附近，因此，风洞试验模拟地貌介于《建筑结构荷载规范》（GB50009—2012）［12］中规定的B类与C类之间，通过在试验段上游设置尖劈和粗糙元来实现。试验风速为10 m·s-1。试验模型以及风洞布置如图4所示。风洞实际风场实测平均风剖面和湍流度剖面如图5所示。图5中z为实测高度，zref为参考高度100 cm，α为拟合风剖面指数，U（z）为实测高度处的平均风速，Uref为参考高度100 cm处的平均风速，Iu为湍流度。参考高度100 cm处脉动风功率谱如图6所示，图中n为频率，Su（n）为顺风向风速功率谱，σ为均方根，Lux为纵向脉动风湍流积分尺度。

图4 试验模型与风洞布置Fig.4 Model of the three-plate billboard in a wind tunnel

图5 平均风剖面与湍流度剖面Fig.5 Profiles of mean wind speed and longitudinal turbulence intensity

图6 参考高度100 cm处纵向脉动风速谱Fig.6 Power spectrum of longitudinal turbulence at 100 cm above the ground

1.3 试验工况

广告牌结构来流风向角设计如图1b所示。根据试验模型的对称性，选取三面广告牌试验风向角为0°～60°，增量为15°，共5个风向角。压力信号采集系统为ESP64-HD型电子压力扫描阀，采样频率为300 Hz，每个工况的采样时长为135 s，根据试验模型缩尺比，对应的实际采样时长约为10 min。

2 数据分析方法

根据试验测得各点风压时程。由于实际的面板厚度很小，每点所承受的风力均为面板正反两面的合力，即净风压Pij。本文规定以指向三面板中心的压力为正，远离中心为负。

各测点风压系数按下式计算：

式中：i为面板编号，i=1，2，3；j为测点编号，j=1，2，…，84；计算时对应的Pij为净风压；CPij为面板i上测点j的风压系数；ρ为空气密度；vref为参考点处的平均风速，参考点为模型顶部高度。图5中风洞试验中湍流度稍偏小，会使得脉动风压偏小，但不会对平均风压和气流分离后的面板负风压极值的测量结果有显著影响。

3 面板风压系数分布

3.1 平均风压系数

根据图1b所示，各板风压以指向三面板中心为正，远离中心为负。经过计算，图7分别给出了0°～60°各风向角下，三面广告牌各面板上平均风压系数的分布规律。

可以发现：0°风向角下，面板1的平均风压系数均为正值，分布均匀对称，平均风压系数出现最大值为1.4；面板2和面板3的平均风压系数分布基本对称。由于为开敞板，气流分离区域风压为0左右，气流再附区域及尾流区域风压为正值，但小于0.2。

15°风向角下，面板1最大平均风压系数仍为1.4，但最大值区域向上游偏移；面板2平均风压系数较小，以正值为主，边缘为负值；面板3平均风压系数也以正值为主，下游位置出现最大值0.3，仅在分离边缘出现较小的负值。

30°风向角下，面板1平均风压系数均为正值，沿面板长度方向，由靠近来流一侧的1.4迅速减小到另一侧的0.2；面板2平均风压系数主要为负值；面板3大部分区域的平均风压系数为正值，负值仅仅分布在面板左边缘。

45°风向角下，面板1平均风压系数仍为正值，并沿面板长度方向由靠近来流一侧的1.4逐渐减小到另一侧的0.2；面板2平均风压系数均为负值，下游区域的上部出现最大负值－1.2，为所有工况下的最大负压；面板3平均风压系数在下游区域出现最大负压－0.4，上游区出现最大正压为0.6。

60°风向角下，面板1和面板3平均风压系数为正且两者对称，都沿着来流方向呈减小的趋势，面板1在1.2～0.2之间变化，面板3在0.8～0之间变化。处于背风面的面板2平均风压系数呈现负值，中心偏上出现最大值－1.2，边缘部分为－0.2。一方面是由于面板2处于背风面气流分离区而产生了负压；另一方面由于开敞布置，来流也可直接作用于面板2的背面。

图7 面板平均风压系数分布Fig.7 Distribution of mean pressure coefficients on the plates

为了防止面板在强风下撕裂破坏，针对面板与龙骨连接进行抗风设计。将0°～60°风向角下，三个面板的平均风压系数进行包络，以朝结构中心为正方向，给出三个面板对应相同位置处风压系数的包络图，即最大平均正风压系数及最大平均负风压系数分布，如图8所示。

图8 三面广告牌面板最大平均风压系数分布Fig.8 Distribution of largest mean wind pressure coefficient in all wind directions for the plates

由图8a可知，最大平均正风压系数基本呈对称分布，面板中部大部分区域平均正风压达到1.4，面板左侧边缘及上部边缘最大值为1.8；最大平均负风压在面板两侧的分布不对称，如图8b所示。由于三面板的围合，板左右两侧平均负风压较小，上部边缘中部气流分离区域平均负风压较大，最大值为-1.4。上述平均风压数值与文献【7】测试的结果非常接近，且随风向角变化趋势亦非常吻合。总体而言，在所有风向角下，最大平均正负风压基本出现在面板边缘和角部区域。故在面板设计时，对于这些部位应当考虑较大的局部风压系数，以提高面板连接设计的抗风可靠度。

3.2 极值风压系数

广告牌面板及连接结构的设计通常需要考虑最不利风压的作用。不同的来流风向角下，面板风压及非高斯区域的分布各不相同。面板中部的脉动风压往往呈现出高斯性，而面板边角位置来流分离的局部区域，脉动风压往往呈现出非高斯性。

因此即使在面板整体平均风压系数不大的情况下，往往由于面板局部极值风压系数偏大而导致面板连接的破坏，引起破坏后风压分布的变化，进一步引起整个面板的连续破坏。因此在进行面板连接结构设计时，需同时考虑风向角及局部极值风压。合理的极值需要采用极值理论对样本进行分析得到。Rice基于泊松假设和零值穿越理论，给出标准高斯过程的极值概率分布如下：

式中：u为标准高斯风压时程；v0为平均穿越率；T为采样时长。

高斯分布的脉动风压的极值计算采用Daveport［13］提出的峰值因子法。峰值因子的计算公式为

已有的研究表明，对于非高斯风压过程，按照高斯过程假设得出的峰值因子取值明显偏小，非高斯分布的风压导致结构破坏的风险要比高斯分布的风压大［9，14-15］。因此非常有必要对非高斯风压的极值做出精确的估计。本文首先采用偏度和峰度统计矩方法判定非高斯分布［16-17］。然后采用Hermite矩方法计算了非高斯测点的极值风压［18-19］。

对于非高斯风压时程，可先经过标准化处理为均值为0，方差为1的硬化或者软化标准非高斯过程x，再通过式（3）转化为标准高斯过程，即

式中：ξ(x)=1.5 b(a+x/c)-a3；a=h3/3h4；b=1/3h4；c=(b-1-a2)3。h3和 h4可由偏度和峰度计算得到。将u代入式（2），再经过转换即可得到标准非高斯过程的极值分布，继而计算出极值风压的期望作为极值风压。

经过上述计算，图9给出了各面板上极值风压系数的分布规律。与图7对比可知，面板极值风压系数分布规律与面板平均风压系数分布规律非常相似。需指出，60°风向角下，面板1靠近来流的左侧边缘区域出现了2.5的最大正压值；30°～45°风向角下，面板2的中间靠近尾流区域出现最大负压值-2.0。

进一步，将上述所有风向角下，三个面板的极值风压系数进行包络，以朝结构中心为正方向，给出三个面板相同位置处极值风压系数的包络图，即最大正风压及最大负风压分布，如图10所示。

图10给出了三面广告牌三个面板在所有风向角下的最大极值风压系数分布。由图10a可知，面板中心处正压达到2.0，面板上部边缘及角部出现最大正压极值为2.4～2.6；最大负压极值的分布如图10b所示，在面板右侧上下边缘达到最大负压极值为-2.4。值得注意的是，在所有风向角下，最大正负风压极值都出现在面板边缘和角部区域。进行面板设计时，对于这些部位应当考虑较大的局部风压系数，以提高设计的抗风可靠度。

4 各面板的风荷载的体型系数

当进行三面板水平支撑型钢梁或者桁架结构的抗风设计时，需要知道三个面板的风荷载体型系数。将0°、30°、60°三个典型风向角下，各板沿面板长度方向上布置的每列测孔的净风压进行平均，可得到这14列测点的平均风压系数C1～C14，如图11所示。将图11进一步在分布形状上进行简化，可以得到可用于设计的更加直观的平均风压简化体系系数的分布，如图12所示。可以发现，如3.1节中的图7一样，在0°和60°风向角下简化体型系数的分布呈现出明显的对称性。

5 面板整体的风力系数

当计算三面广告牌独立支撑柱的风荷载时，与前述不同，需要将三个面板视为整体，来计算广告牌上部结构整体的x方向、y方向、水平合力及扭矩的风力系数。单个面板的风力系数CFi和扭矩系数CTi可定义为

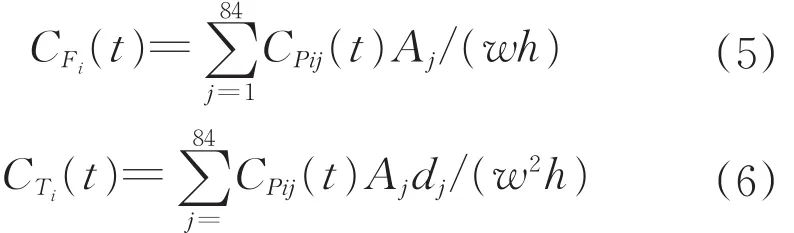
式中：Aj和dj分别为j测点的从属面积和该点到面板竖向中轴线的力臂；w和h分别为面板的宽度和高度。扭矩系数通常也被称为垂直于面板风力的偏心率。

根据图1b所定义的坐标系及面板之间的夹角θ，将各面板力系数合成得到结构整体的x方向和y方向风力系数以及扭矩系数为

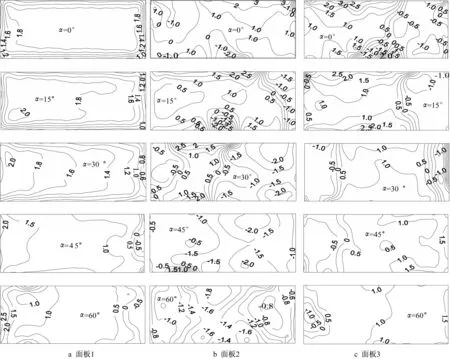
图9 面板极值风压系数分布Fig.9 Distribution of extreme pressure coefficients on the plates

图10 三面广告牌面板最大极值风压系数分布Fig.10 Distribution of envelop of extreme wind pressure coefficient in all wind directions for three-plates

水平合力系数可由x方向和y方向风力系数得到，如式（10）所示，其均值、均方根和极值如图13所示。

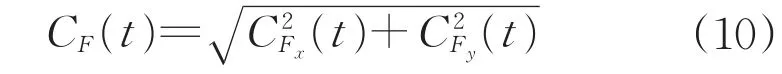
可以发现，y方向风力系数CFy随风向角的增大而减小，最大的均值和极值出现在0°风向角，分别为1.18和1.50，对应的峰值因子为3.40；x方向风力系数CFx随风向角增大而增大，最大的均值和极值出现在60°风向角，分别为0.92和1.14，对应的峰值因子为3.37；随风向角增大，水平合力系数CF变化不大，最大的均值和极值都出现在0°风向角，分别为1.20和1.53；扭矩系数CT在30°风向角时有最大的均值和极值，分别为0.102和0.174，对应的峰值因子为3.30。此外，x方向和y方向风力系数均方根随风向角增大基本不变，扭矩系数均方根随风向角增大略有减小。

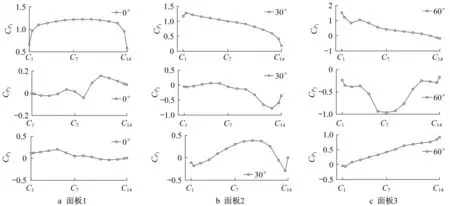
图11 平均风压分布系数Fig.11 Mean wind pressure distribution coefficient

图12 0°、30°、60°风向角时三面板的简化体型系数Fig.12 Simplified shape coefficients of three plates at wind direction angles of 0,30,and 60 degrees

图13 结构整体风力系数Fig.13 Force coefficient of overall three-plates

6 结论

（1）不同风向角下，三个面板上的风压变化有明显的规律性。0°风向角下，迎风面板的平均风压系数出现了最大的正值，且由于开敞布置，相邻面板也表现出较小的正值；30°风向角下，迎风面面板的平均风压系数虽然为正值，但沿来流方向分压呈渐减分布。背风面板2的平均风压系数主要为负值，面板3的平均风压系数主要也为正值；60°风向角下，面板1和面板3的平均风压系数为正且二者对称，并沿着来流方向呈渐变减小的趋势。处于背风面的面板2平均风压系数呈现最大负风压。

（2）三个面板在全部风向角下的平均正风压包络呈现出中心对称分布，最大值分布在边缘，由0°风向角下迎风板控制；平均负风压的包络呈两边对称，最大值分布在上下边缘的中部，由60°风向角下背风面板控制。因此，面板抗风设计中应注重局部风压系数的取值。

（3）依据测点的平均风压系数，本文进一步给出了适用于设计的简化的面板体型系数分布，可作为面板水平支撑体系的风荷载取值的依据。

（4）从结构整体风力系数来看，y方向风力系数随风向角的增大而减小，x方向风力系数随风向角增大而增大，水平合力系数随风向角增大变化不大，最大水平合力系数达1.53，扭矩风力系数在30°风向角时达到最大，约为0.174。