物理与圆的不解之缘

■杨新凯

圆是完美的象征，在物理学中圆的应用非常广泛，物理与圆有着不解之缘。在求解物理问题时，结合物理规律和方法中隐含的“圆”的特征，大胆进行联想、变通、类比和迁移，会产生“四两拨千斤”之奇效。

一、矢量圆：柳暗花明，豁然开朗

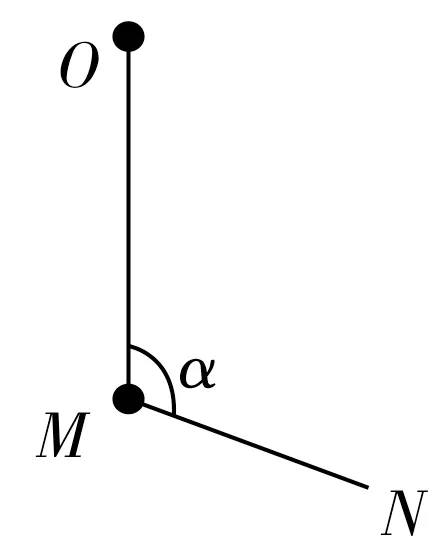
图1

例1如图1，柔软轻绳ON的O端固定，其中间某点M拴一重物，用手拉住轻绳的N端。初始状态OM竖直且MN被拉直，OM与MN间的夹角为。现缓慢将重物向右上方拉起，且保持夹角α不变。在OM由竖直被拉至水平的过程中，轻绳MN、OM段的张力如何变化?

分析：重物受三力平衡，其中只有重力恒定不变，且轻绳MN、OM段张力F1、F2的夹角不变，而大小与方向均发生变化，根据同一圆弧对应圆周角不变的几何特点，可将三个力平移入矢量圆中，如图2，以mg为 固 定 弦，P点在圆上移动，因此在OM由竖直被拉至水平的过程中，F1逐渐增大，F2先增大后减小。

图2

二、等时圆：巧用推论，快速制胜

例2如图3，在同一竖直线上有A、B、O三 点，其 中A、B两点相距h，B点离地高度为H，O点在地面上。现要在地面上找到一点C，使得物体由静止沿从A、B两点分别向C点安放的光滑木板滑动时，满足运动时间相等。求O、C两点间的距离。

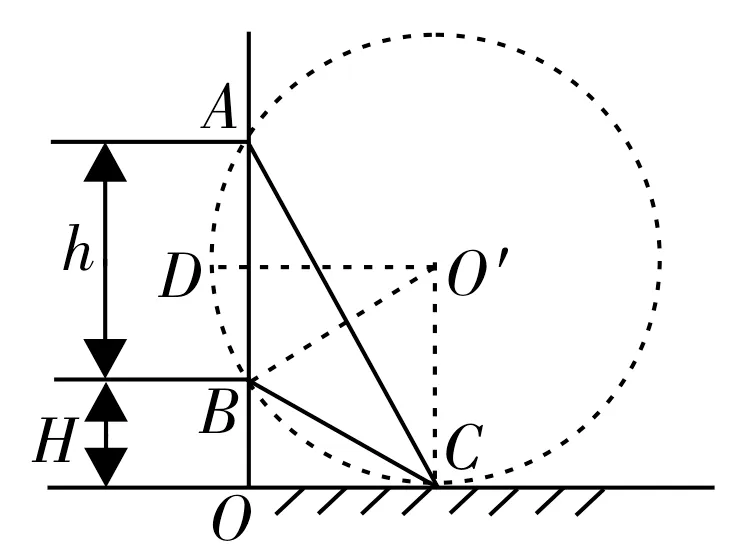
图3

分析：竖直平面内有一固定圆周，小物体从圆周上的各点出发分别沿光滑斜面由静止开始下滑到圆周的最低点，时间均相等(证明略)。该题中若A、B、C三点分别是竖直平面内等时圆圆周上的三个不同位置，且C点是最低点，AC和BC分别是等时圆的两条弦，则C点满足题意。画出过A、B两点并与地面相切的圆，切点为C。由几何关系得

三、等势圆：独辟蹊径，峰回路转

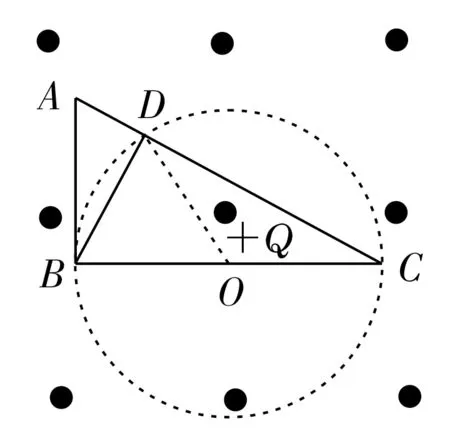
图4

例3如图4，倾角为30°的直角三角形底边长2L，斜边为光滑绝缘导轨。整个装置处于磁感应强度为B0的匀强磁场中，方向如图。现在底边中点O处固定一正点电荷Q，让一质量为m的正点电荷q从斜面顶端A处由静止释放沿斜面滑下(不脱离斜面)。现测得它滑到B点在斜边上的垂足D点处的速度为v0，求该点电荷滑到斜面底端C点时的速率v。

分析：点电荷q在沿DC运动的过程中，洛伦兹力不做功，静电力的大小和方向不断变化，因为DO=CO=BO，所以可作出以O为圆心的等势圆，则点电荷q从D点运动到C点的过程中，静电力不做功，仅重力做功，由动能定理得，由几何关系得，解得

四、动态圆：动态思维，举重若轻

例4如图5，在范围内有垂直于xOy平面向外、磁感应强度为B的匀强磁场。某时刻在坐标原点O处的一粒子源发射大量质量为m、电荷量为+q的粒子，它们的速率相等，速度方向均在xOy平面内，与y轴正方向间的夹角范围是0～90°。已知粒子在磁场中做圆周运动的半径在a之间，从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一，求最后离开磁场的粒子从粒子源射出时速度方向与y轴正方向间的夹角的正弦值。

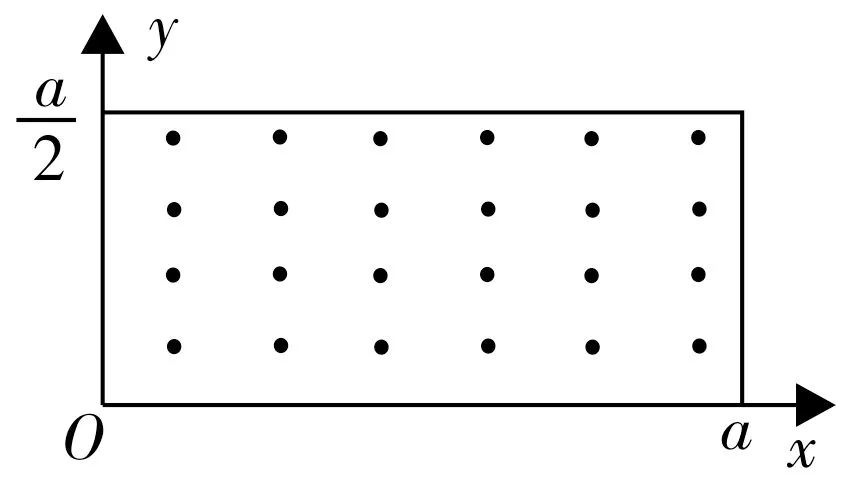
图5

分析：作出从不同方向射出的粒子的运动轨迹，通过旋转定圆，分析粒子运动圆轨迹对应弦长的变化可得，最后离开磁场(在磁场中运动时间最长)的粒子其轨迹圆应与磁场的上边界相切，如图6。当时，在磁场中运动时间最长的粒子其轨迹是圆心为C，与磁场的上边界相切于D点的圆弧，设该粒子在磁场中运动的时间为t，则当时，∠OCA=。设最后离开磁场的粒子的发射方向与y轴正方向间的夹角为α，由几何关系得，再结合sin2α+cos2α=1，解得。

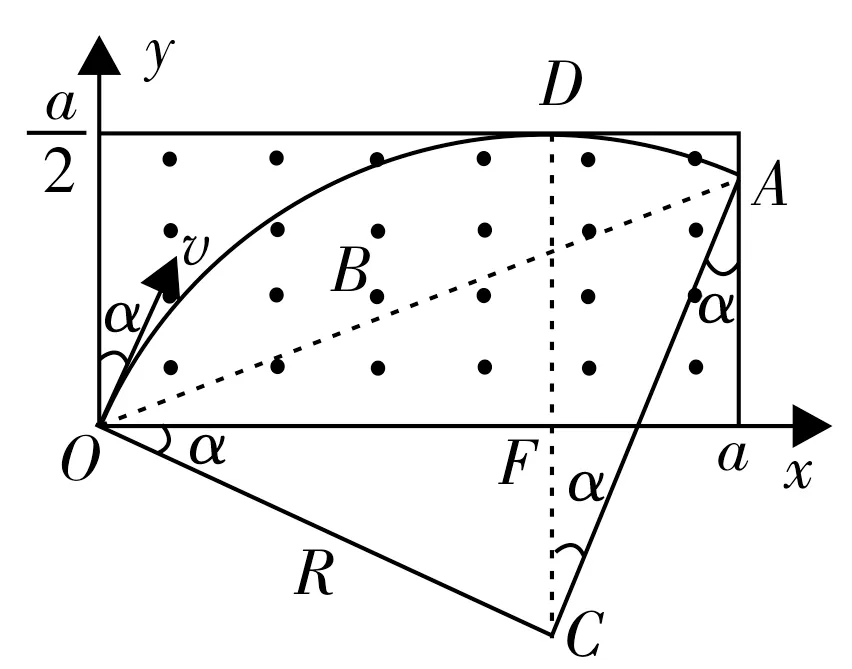
图6