巧妇能为无米之炊——以三角方程为例

■赵 炜

一般来说，一个方程一个未知数，两个方程两个未知数才能够解出唯一解。但是我们在高中数学的学习中往往会发现一些反常的情况，比如一个方程两个未知数能够解出唯一解，又如两个方程五个未知数能够解出一个定比例关系。对于这种未知数个数多于方程个数的情况，下面我们就以三角方程为例进行分析。

一、一元二次三角方程

例1设α，β∈(0，π)，且cosα+cosβ-，求α，β的值。

评注：对于一元二次三角方程，一般情况下解是不确定的，只有特殊情况下才有定解。特殊情况主要有非负数之和为0，基本不等式取等号，一元二次方程判别式为0等。

二、二元一次三角方程组

例2已知cosα+cosβ=，sinα+sinβ=，求cos(α-β)。

解：两式平方相加得2+2cos(α-β)=，推出cos(α-β)=。

评注：这是人教版教材必修四P147的一道习题，它本质上是四个方程四个未知数(考虑到sin2α+cos2α=1，sin2β+cos2β=1)，但用解方程的方法解出这四个未知数再计算cosα-β( )将会非常烦琐。

希尔伯特说过：“数学问题的宝藏是无穷无尽的，一个问题一旦解决，无数新的问题就会取而代之。”如果我们思考更一般的问题呢?

问题1：设cosα+cosβ=m，sinα+sinβ=n，当m，n∈R满足什么条件时有解?

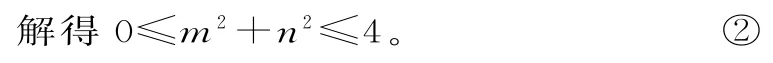
由万能公式得

问题2：α，β的具体值能求出吗? (有些同学对例1 的方法始终难以接受，因为我们始终未把α，β求出来，下面我们就利用反三角函数把α，β表示出来)

解：由问题1中的①③两式知

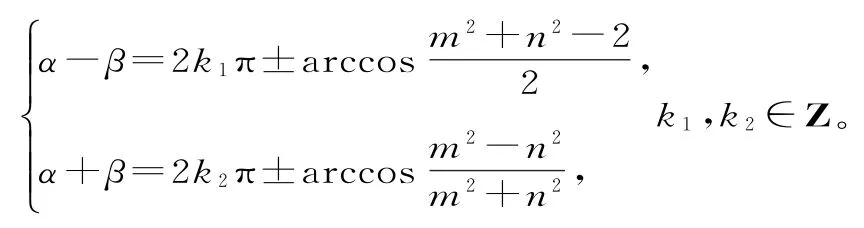
评注：两式相加减即可解出α，β。当然，一般情况下α，β有无穷多组解。即使取k1=k2=0，考虑到方程组两式各有正负性两种选择，此时α，β也有四组解。

三、多元一次三角方程组

例3已知abc≠0，φ+θ≠mπ，φ-θ≠nπ，m，n∈Z，且求证：。

解法一：两式相减得a(cosθ-cosφ)+b(sinθ-sinφ)=0，和差化积得·，即，所 以。设，则a=。

代入原式得c=kcoscosθ+。所以。

解法二：已知两点A(cosθ，sinθ)，B(cosφ，sinφ)都在直线ax+by=c上，但点A，B又决定一条直线(cosθ-cosφ)(y-sinφ)=(sinθsinφ)(x-cosφ)，化 简 得xcos+。又因为两点确定唯一一条直线，所以两直线重合，故有对应系数成比例，即。

评析：本题只有两个方程，而却有a，b，c，θ，φ五个未知数，解题时很容易陷入不知所措的境况。解法一观察到两式相减可以消去变量c，通过解出a，b的比例关系，代入原式寻找c的比例关系，逐层推进，是一个可行的方法。而解法二则更胜一筹，通过观察方程的几何意义，推导出本题的数学本质，免去了烦琐的计算。

例4已知0＜α＜β＜γ＜2π，且sinα+sinβ+sinγ=0，cosα+cosβ+cosγ=0。求β-α的值。

解法一：代数法。由条件得sinα+sinβ=-sinγ，cosα+cosβ=-cosγ，两式平方相加得2+2cos(β-α)=1，则cos(β-α)=。

因为0＜α＜β＜γ＜2π，所以β-α=或。同理可证γ-β=。若βα=，则γ=(γ-β)+(β-α)+α≥++α＞2π，矛盾。故β-α=。

解法二：向量法。设=(sinα，cosα)，)，则原条件化为，，则β-α为向量的夹角，移项得。两边平方得cos(β-α)=，解得cos(β-α)=-。后同解法一。

总结：解法二实际上证明了一个在单位圆上的三个点组成的△ABC满足重心和外心重合于坐标原点，则△ABC为正三角形，从而β-α=γ-β=。

综合例3、例4我们可以看出，多元的三角方程问题如果就题论题，常常会一叶障目，不见泰山，导致计算过程相当烦琐，很可能走弯路。如果从更高的观点来看，找出题目的几何意义或物理背景，往往能够思路更清晰，计算更简洁，取得事半功倍之效。