基于键合图理论的定轴齿轮传动耗散特性研究

齐焕敏， 程联社

（杨凌职业技术学院机电工程分院，陕西咸阳712100）

0 引 言

齿轮传动是机械领域中最常见的一种传动方式，由于齿面摩擦、时变刚度、齿侧间隙等非线性因素的存在[1]，使得齿轮传动的效率大打折扣。对任意一种传动方式来说，均需在单个齿对传动的基础上来完成，对其动、静态性能的研究显得尤为重要。为此，国内外学者提出了很多具有不同特点的力学方法及软件，键合图就是其中一种[2]。

系统键合图以能量守恒的基本原则为依据，将整个系统由一些基本元件以一定的连结方式用规定的符号来表示[3]。近年来国内外诸多学者将其用于机械系统的建模，进行运动学和动力学方面的研究。唐进元等[4]建立了含有间隙和摩擦的齿轮键合图模型，但模型中没有将摩擦力与主从动轮的啮合联系起来，有一定的局限性；张宝锋等[5]构建基于NGW型行星轮系的键合图模型，以XP型和PX型单环路行星系统为例，计算其输出转速和啮合传动效率，但其研究范围偏向于稳态；何雅槐等[6]根据杆件的几何关系，确定单个杆件质心的运动规律与旋转副或滑动副的关系，建立包含旋转副或滑动副的键合图模型及摆动导杆机构的键合图模型，为复杂平面连杆机构键合图建模提供一种新思路；陈素丽等[7]针对于齿条钻机工作时的精确对中这一问题，提出了可以沿着钻井架轨道自由升降的轨道钳系统，并用键合图理论建立了对应数学模型并仿真，为升降系统的研制和控制提供技术指导。

在现有文献中，专门用键合图研究齿轮对之间摩擦耗散与效率之间的关系几乎没有，因此，本文根据单对齿轮啮合的基本原理，建立齿轮内外啮合基于摩擦的基本键合图模型，对不同啮合状态下齿轮啮合耗散特性进行研究。并由此对定轴轮系耗散特性进行研究。

1 齿轮传动啮合过程

轮齿在啮合过程中的一个啮合周期是以双齿共同承担载荷开始，经过单齿啮合过程，最后以双齿啮合来结束。假定齿轮1、齿轮2分别为主、从动轮，结合陈立峰[8]提出的圆盘模型建立一对齿轮外啮合与内啮合的运动学模型分别如图1、图2所示。

假设，主从动轮在K点啮合，其速度分别为VK1和VK2，此时相对速度VS为

根据内外啮合的不同, 其啮合线分别遵循式（2）、式（3）的关系

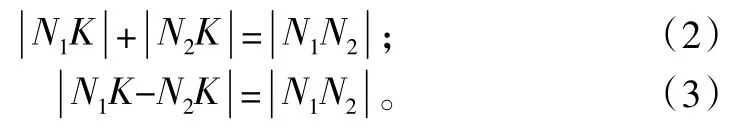
将整个啮合线按照齿对所处位置不同分为4个区间，如图3所示，其中1、4为双齿啮合区，2、3为单齿啮合区。

2 单齿传动耗散特性分析

图1 齿轮外啮合运动模型

结合图1～图2，将摩擦力对主动轮1 所做功率记为Pf1，对从动轮2 所做功率记为Pf2，可以得到:

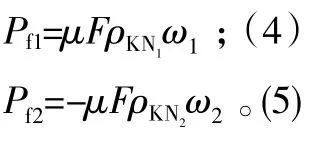
式中：μ为摩擦因数，根据传动条件及润滑要求，可近似取平均摩擦因数来计算；F为相互啮合时齿面所承受的载荷，与齿面法向总载荷FN有关；ρKN1、ρKN2为啮合点K在两圆盘上的曲率半径，ρKN1=|KN1|，ρKN2=|KN2|。

图2 齿轮内啮合运动模型

图3 啮合区间示意图

在某一瞬时，啮合中单个齿对的功率损耗Pf为主动轮与从动轮所受摩擦功率之和，于是齿轮传动过程中单个齿对沿着啮合线运动时的瞬时摩擦功耗Pf为

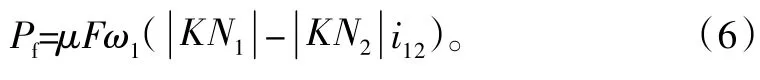
式中：i12= ±z2/z1，外啮合取“-”，内啮合取“+”；F为齿面所受载荷，对其具体取值进行如下讨论。在单齿啮合区时，只有一个齿对进行啮合，该齿对承受所有载荷，在双齿啮合区，前、后两齿对共同分担齿面所受载荷。将啮合点K所在齿对所承受压力F与齿面法向总载荷FN之间的关系用载荷分配系数β来表示，它们之间存在关系

式中：

以外啮合为例，将啮合点K在区间1、2、3、4不同位置时的啮合传动情况[9]如图4所示。

本小节我们仅研究啮合点K所在齿对的功率损耗情况，不考虑在啮合过程中前一对或后一对的功率损耗。结合式（6）～式（9），输入转矩T1及速度ω1由系统给定，要确定损耗功率Pf，还需要确定参数包括：rb1、i12、|KN1|、|KN2|、|B2K|、|B2C|、|B2D|。

用基本的z、m、α、ha*、c*所有表示参数，具体的求解过程如下：

分度圆半径：r1=mz1/2，r2=mz2/2；基圆半径：rb1=r1cosα，rb2=r2cosα；齿顶圆半径：ra1=r1+ha*m，ra2=r2+ha*m。

图4 K在不同区间时啮合传动示意图

记K在B2处刚进入啮合时，主动轮压力角：α1s=arctan(|N1B2|/rb1) ，一个周期内，啮合点K处主动轮压力角：α1=α1s+ω1t，齿顶圆压力角：αa1=arccos(α/ra1)，αa2=arccos(α/ra2)，基圆齿距：pb=πmcosα，在啮合过程中，|N1B1|=rb1tanαa1，|N2B2|=rb2tanαa2。

当单齿对处于外啮合状态下时，有：

当处于内啮合状态时，小齿轮为主动轮，有：

由此，将式（6）中所有未知参数表示出来，完成一个齿对在外啮合或内啮合过程中的功率损耗情况分析。

3 单齿传动键合图仿真分析

为了对上述单齿对啮合功率损耗分析的正确性进行验证，假定z1=24，z2=81，模数m=2，压力角α=20°。给定输入转矩TI=1 N·m，输入转速ω1=1 r/min，用20-sim软件建立键合图模型，对K点在一个周期内任意位置的功率损耗及效率情况进行仿真。

建立单齿轮传动键合图模型如图5所示。内、外啮合键合图模型仅仅为参数设置上的不同。

图5 单齿传动键合图模型

3.1 外啮合状态下仿真分析

记输入功率和输出功率分别为P1、P2，那么在啮合过程中损耗的功率用P3=P1-P2表示，单位为W。外啮合情况下单个齿对在啮合线上运动时的功率损耗及效率曲线分别如图6和图7所示。

图6 外啮合功率损耗

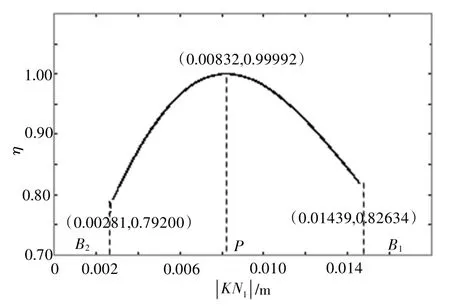
图7 单齿外啮合效率

可以看出，当啮合点处于中间节点P位置时，由于啮合所引起的功率损耗最小，同时效率也最高，距离节点越远，功率损耗越大，对应的啮合效率越小。

3.2 内啮合状态下仿真分析

用同样的方法对内啮合下单个齿对的功率损耗及效率曲线进行绘制，如图8、图9所示。

可以看出，在同样的参数配比情况下，内齿啮合效率要高于外齿啮合。由于图6～图9所示仅代表一个齿对在啮合线上运动时的功率损耗及啮合效率，事实上在一对齿轮进行传动的过程中，存在双齿啮合区，两个齿对的效率综合起来将会是一对齿轮传动的啮合效率。

4 单对齿轮传动功率损耗

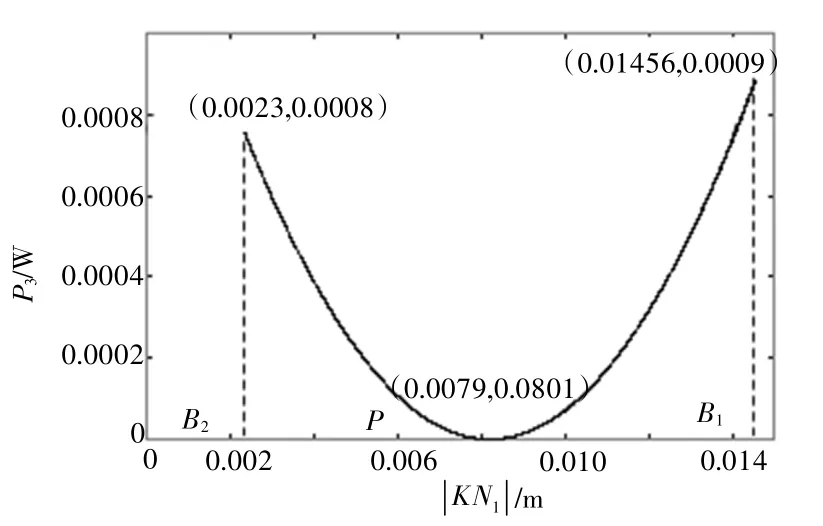
图8 内啮合功率损耗

图9 单齿内啮合效率

对于由一对齿轮传动组成的轮系，应用上节所述的研究方法，在计算功率损耗时，不但要计算齿对K上的功率损耗，还要计算不同时刻可能出现的，其前一对或后一对齿的功率损耗情况。记齿对K的上一齿对为K1，下一齿对为K2，具体齿对在各个区间的啮合情况在图4中已经表示，这时齿轮传动中一对齿轮啮合的功率损耗同样为摩擦力对齿轮1与齿轮2做功之和。

1）当齿对K在区间1内啮合时，损耗功率为主动轮1在啮合点K、K1处功率损耗与从动轮2在啮合点K、K1处功率损耗之和，即

2）当齿对K在区间2、3内啮合时，损耗功率为主动轮1在啮合点K处功率损耗与从动轮2在啮合点K处功率损耗之和，即

3）当齿对K在区间4内啮合时，损耗功率为主动轮1在啮合点K、K2时的功率损耗与从动轮2在啮合点K、K2时功率损耗之和，即

结合图4可知，齿对K在区间1内时，有

齿对K在区间4内时，有

结合以上分析，将式（10）～式（14）整理并化简可得单对齿传动时的瞬时损耗功率为Pf（β）=

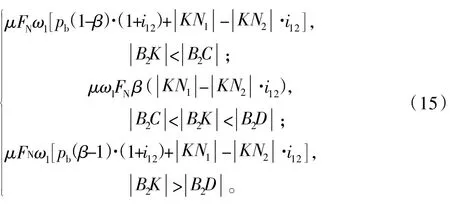
式（15）同样适用于内啮合，式中各参数的计算公式与2节中参数公式相同。

5 定轴齿轮传动耗散弹性研究

定轴轮系中各齿轮对依次串联，于是对于由n个齿轮对串联而成的支路，其瞬时功率损耗应为

用η～表示该串联支路的效率，则

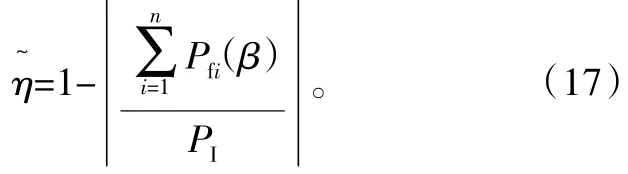
6 结 语

本研究从齿轮传动的运动学模型入手，首先对啮合点处于不同啮合位置时的单齿传动耗散特性进行研究，并通过建立键合图软件对其进行仿真分析，在此基础上，对单对齿轮传动瞬时功率损耗情况进行研究，并得出定轴轮系在任意瞬时的效率计算方法。

本文假定机械传动的摩擦因数为定值，后续研究应根据齿轮具体工作环境及试验条件来选择合适的摩擦因数值，进行更精确的分析。在此基础上，可将该模型推广至周转、差动传动的分析中，为轮系的研究提供新的思路。