基于图像处理的逐次逼近式位置随动系统

赵子达， 高艺， 孙克彬

(长春理工大学 机电工程学院，长春130022)

0 引 言

近年来，图像处理技术突飞猛进，其应用范围越来越广泛。通过图像处理技术，对某些物体进行跟踪与定位是一个重要的研究方向。通过摄像头对物体定位，控制机器人的移动跟踪，这也是移动机器人研究方向的热点[1]。本文采用逐次逼近的方式，对机器人进行位置随动控制，实现其准确收集乒乓球的功能。

1 系统组成结构及工作原理

基于图像处理的逐次逼近式位置、速度双闭环反馈随动系统如图1所示。硬件系统包括STM32F103RCT6控制器（以下简称为STM32）、电动机驱动、电动机、光电编码器、openMV摄像头（以下简称为摄像头）及球场智能服务机器人整体机械结构（以下简称为机器人），通过串口通信（USART）、图像处理、速度PID调节、PWM脉冲输出及逐次逼近式位置控制器，实现系统工作。

图1 系统工作流程图

图2 机械运动结构图

通过摄像头对乒乓球位置信息进行采集，将乒乓球的实际二维位置信息处理成摄像头内部的二维位置信息，并将其通过串口发送至STM32。STM32接收到位置信息后，对位置信息进行判断，即判断乒乓球与机器人的相对位置是否在规定区域内，如不在，则控制电动机转动，使机器人旋转移动，逐步使乒乓球与机器人的相对位置符合要求，进而通过机器人的拾球机构实现对乒乓球的拾取。

为了保证机器人旋转的精度，使用速度闭环保证旋转速度的稳定，同时摄像头不断采集乒乓球与机器人的相对位置，利用闭环位置控制，保证拾取精度。

2 机械运动结构

系统的机械运动结构如图2所示。

通过4个电动机带动全向轮进行旋转，实现对机器人的全方位水平运动控制。光电编码器位于电动机后方，将电动机输出轴的角位移转变为脉冲信号，对电动机进行测速。摄像头与单片机系统固定于机器人上方平台，摄像头有一定高度，倾斜放置一定角度，以方便对乒乓球所在的实际二维平面的相对位置进行采集。

3 相对坐标系与图像坐标系

相对坐标系，即以机器人为参考系的坐标系，机器人与乒乓球都位于该坐标系下进行运动。由于摄像头位于机器人之上，且具有相对高度和一定倾斜度，则摄像头采集的数据信息其实是以摄像头视角的图像坐标系。

这两个坐标系应该具有固定的相对关系，但这个相对关系是未知的，这就给机器人的乒乓球拾取工作造成困难。摄像头采集的乒乓球位置信息是基于图像坐标系的，而机器人在相对坐标系下运动，未知的关系造成了图像坐标系下的位置信息无法直接应用于相对坐标系，为此，可以采取逐次逼近的方法，忽略未知关系的定量关系，直接对其进行定性分析。

基于实际机械运动结构，首先将机器人和乒乓球放置在同一平面。然后以平台的几何中心作为原点，以机器人的正方向作为Y轴的正方向，以垂直于Y轴向右的方向作为X轴的正方向，建立一个相对坐标系。这样可以测量出乒乓球的坐标位置，称为相对坐标。此时也可以使用摄像头进行位置读取，以摄像头检测范围的右上角像素点为原点，沿下方为Y轴正方向，沿右方为X轴正方向，则建立了一个图像坐标系。可以读取出乒乓球在该坐标系的坐标位置，称为图像坐标。

图3 相对坐标系

图4 图像坐标系

移动乒乓球，使乒乓球在相对坐标系下，沿X轴正方向运动，即实际坐标X增大，Y不变，观察图像坐标变化。同时再使乒乓球沿Y轴正方向运动，即相对坐标Y增大，X不变，观察图像坐标变化。最后使乒乓球作以原点为圆心、半径为R（以图中为例）的运动，同样观察图像坐标变化，得到表1。

表1 相对坐标系与图像坐标系定性关系

通过表1可以得出，乒乓球在相对坐标系下的改变与在图像坐标系下的改变具有定性的关系，这就使逐次逼近型系统的实现成为可能。

4 位置随动系统中的速度闭环

对于整个系统，电动机是系统最主要的运动部件。为了保证系统的精度，首先使用PID算法对电动机的速度进行闭环控制，以光电编码器作为测速器件，实现速度反馈[6]。

由于系统属于随动系统，对快速性要求比较高，所以对速度控制采用PID调节器进行调节，全面提高速度内环的性能。

图5 速度闭环系统组成原理框图

5 逐次逼近式位置随动控制

为了实现机器人的拾取功能，系统需要将机器人与乒乓球的相对位置调整到一定范围内，为此，可以将二者相对图像位置作为信息输入量，通过电动机不断调整相对位置，逐步逼近规定位置。

为此，可以建立一个以机器人平台几何中心O为极点，以机器人的正方向的射线为极轴L的极坐标相对坐标系[7]。则实际平面的任意一点都可以使用角度β与半径R表示，如图6所示。所以，只要确定相对坐标系下符合要求的规定区域在图像坐标系下的范围，即可对此范围进行反馈，从而逐步使相对关系符合要求。

为了测量图像坐标系下的规定范围，首先将该规定范围沿L方向延长为规定区域1，此时这个区域在图像坐标系下，可以由两条直线之间的区域表示。

图6 相对极坐标系示意图

图7 实际坐标系下的规定区域1

图8 相对坐标系下的规定区域1

本文通过测量直线上各点的图像坐标，通过线性拟合得到这两条直线在图像坐标系下的方程。测量数据如表2所示。

表2 相对坐标及其拟合方程

图9 逐次逼近步骤1

图10 逐次逼近步骤2

根据测量数据拟合出来的两条直线R2均大于0.99，说明测量数据无误，也表示该回归拟合的效果很好。

在此坐标系下，若机器人作旋转运动，则乒乓球相对于机器人作圆周运动。由上文可知相对坐标系下乒乓球相对于机器人作圆周运动时乒乓球图像坐标的变化规律。所以先使用逐次逼近使乒乓球角度符合规定区域1的要求，之后只需要将半径R减小，就能实现要求。其步骤如图9、图10所示。

由图10可以看出，步骤2缩短半径的方式主要是走直线，电动机速度主要影响步骤2的完成时间。因此逐次逼近的重点应放到步骤1上，即规定区域1的逼近。当机器人作旋转运动时，θ=ω·t。其中：θ为旋转角度；ω为旋转角速度；t是旋转时间。

逐次逼近要求每次旋转的Δθ适中，才能保证在提高效率的前提下让所有的乒乓球可以逼近到规定区域。为保证所有的乒乓球被收集，首先假设摄像头最远识别距离1000 mm。同时取乒乓球刚好处于边界的时候作为一种极限位置，如果可以保证在该位置时，乒乓球可以逼近到规定区域，则所有乒乓球均可，通过软件模拟计算，求得最小旋转角度Δθmin=2°。

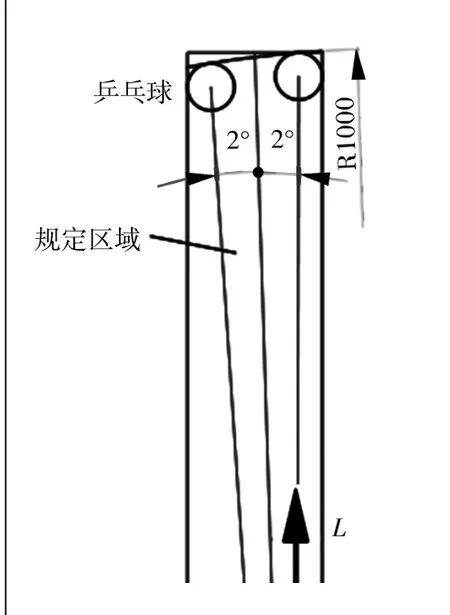
图11 乒乓球极限位置模拟

通常为了提高系统的响应速度，系统要求Δt足够小。而Δt的最小值受到摄像头采集速度和STM32的程序执行速度的限制，即

式中：Δtmin为每次逼近的最短时间间隔；t1为摄像头采集位置信息的发送周期；t2为STM32执行中断程序的执行时间。

为了保证整个逐次逼近过程的连续性，应保证t＞t1+t2，为了保证STM32接收位置信息的完整性，应保证t1＞t2。

在预设好一个旋转时间t之后，我们可以通过调节旋转速度ω的大小，来使整个系统稳定工作。在理想条件下，旋转速度与电动机转速的换算关系为

式中：n为电动机转速；r1为轮子半径；r2为底盘半径。

6 结 语

该位置随动系统忽略了相对坐标系和图像坐标系的定量关系，使用逐次逼近的方式，控制机器人接近目标，对二维平面内的位置信息有较好的跟踪效果。通过样机实验，证实了该位置随动系统的跟踪效果。