不相干算子和强不相干算子的刻画

田 瑞, 陈峥立, 李 蕊

(陕西师范大学 数学与信息科学学院, 西安 710062)

1 引言和预备知识

量子相干性的理论研究目前已成为量子力学、 量子光学、 量子信息学中的重要研究课题, 已被量子信息专家广泛关注[1-9].在双边和多边系统的研究中, 量子相干性和量子关联同等重要.为了对量子相干性的性质进行研究和量化, 并且构建一个更严格和更具有物理意义的数学框架是目前该领域的研究热点[8].Åberg[10]提出了一个量化相干性的公理化方法.Baumgratz等[2]研究表明, 基于距离的相干性度量是l1-范数和相干性的相对熵.Streltsov等[11]提出了基于纠缠和保真度的相干性测量方法; Yuan等[12]提出了基于凸顶结构的相干性测量方法; 文献[13]给出了一些量化相干性的方法.近年来, 随着对量子相干性度量严格定义的提出, 量子相干性已经被视为一种量子资源, 对其进行蒸馏提取与操控成为一个研究热点[9].Streltsov等[1]研究了量子相干性在两体量子系统Alice与Bob中的转化问题; Chitambar等[14]研究了非相干量子运算, 并且给出了不同类别非相干量子运算的比较；文献[5]对量子相干性和几何量子扰乱给出了进一步的研究结果.分析上述研究结果表明, 结合相关知识探讨不相干量子运算所对应的kraus算子分解的特性研究报道较少.

因为上述研究未对不相干量子运算和严格不相干量子运算所对应的kraus算子的具体特性进行刻画, 因此本文运用算子代数和矩阵论的方法对不相干算子和强不相干算子具有的特性进行讨论和研究.首先, 给出有界线性算子是不相干算子当且仅当其为类置换算子和不相干算子的具体表达式, 以及用不相干算子刻画不相干量子运算的结论; 然后给出强不相干算子的具体形式, 进而得到严格不相干量子运算的两个等价定义, 并给出严格不相干量子运算是不相干量子运算的真子集; 最后用实例验证了所给的结论.

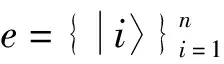
定义1设T∈B(H), 若对任意的ρ∈B(H), 有

Δe(TΔe(ρ)T†)=TΔe(ρ)T†,

则称T关于e是不相干的,T简称为e-不相干算子.否则,T为e-相干算子.

定义2设T∈B(H), 若对任意的ρ∈B(H), 有

Δe(TΔe(ρ)T†)=TΔe(ρ)T†,Δe(T†Δe(ρ)T)=T†Δe(ρ)T,

则称T关于e这组基是强不相干的,T简称为e-强不相干算子.

设{Ek}为量子运算ε的一组kraus算子, 若对任意的k, 都有Ek是e-不相干的, 则称{Ek}是一组e-不相干kraus算子.若对任意的k, 都有Ek是e-强不相干的, 则称{Ek}是一组e-强不相干kraus算子.

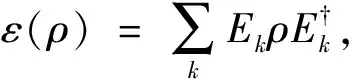
则称ε是B(H)上的一个不相干量子运算.

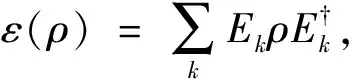
则称ε是B(H)上的一个严格不相干量子运算.

用IO(H)和SIO(H)分别表示B(H)上的不相干量子运算之集和严格不相干量子运算之集.显然SIO(H)⊂IO(H)[11].

2 不相干算子与不相干量子运算

一个量子运算由一组kraus算子描述, 不同的量子运算对应不同的kraus算子.下面首先给出不相干算子的两个刻画, 然后给出相应的不相干量子运算结果.

例1设H=2, 选取e={|0〉,|1〉}, 则是一个e-不相干算子,是一个e-相干算子.

证明: 由于

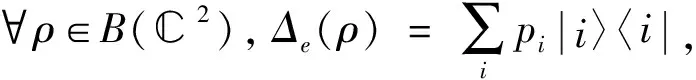
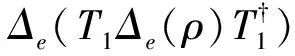
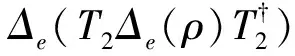
例2设H=2, 选取e={|0〉,|1〉}, 对于任意的其中:则ε属于IO(H).

证明: 由于

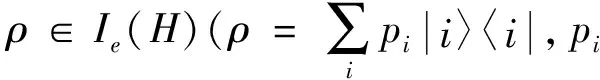
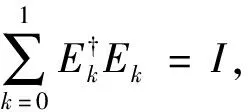
定理1设T∈B(H), 则T为e-不相干算子当且仅当对于任意的|i〉∈e, 存在λi∈, |ji〉∈e, 使得

T|i〉=λi|ji〉.

(1)

证明: 首先证明充分性.设对任意的|i〉∈e, 存在λi∈, |ji〉∈e, 使得T|i〉=λi|ji〉.对任意的ρ∈B(H), 则从而

因此Δe(TΔe(ρ)T†)=TΔe(ρ)T†, 由定义1可知,T为e-不相干算子.

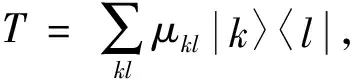
因为T为e-不相干算子, 由定义1可知, 存在λj∈, 使得TΔe(ρ)T†=∑λj|j〉〈j|, 从而

因此

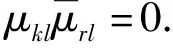
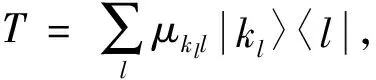
注1由定理1必要性的证明可知, 设T∈B(H), 若T为e-不相干算子当且仅当Te的每列都至多有一个非零元素.

注2设T∈B(H), 若T为e-强不相干算子当且仅当对任意的|i〉∈e, 存在λi,μi∈, |ji〉,|ki〉∈e, 使得T|i〉=λi|ji〉,T†|i〉=μi|ki〉.

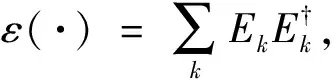
由定理1和注1～注3, 可从一个算子的形式直观判断出它是不相干算子还是相干算子, 进而得出它对应的量子运算是否是不相干量子运算.

注4对于例1中的T1,T2, 从形式上看T1e的每一列都只有一个非零元素,T2e的每一列都有两个非零元素, 由注1和定义1易知,T1是一个e-不相干算子,T2是一个e-相干算子.此外,

由式(1)可知,T1是一个e-不相干算子,T2是一个e-相干算子.

注5对于例2中的E1,E2, 从形式上看E1e,E2e的每一列都只有一个非零元素, 由注1和定义1易知,E1,E2都是e-不相干kraus算子.由注3可知,ε∈IO(H).

定理2设T∈B(H), 则T为e-不相干算子当且仅当存在ck∈,f是从e到e的映射, 使得

(2)

证明: 充分性.设存在ck∈,f是从e到e的映射, 使得则对于任意的|i〉∈e, 有

由定理1可知,T为e-不相干算子.

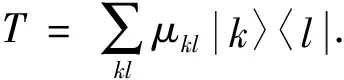
且对于任意的|l〉∈e, 有T|l〉=μkll|kl〉.因此

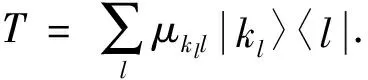
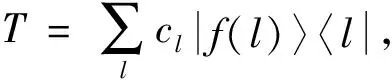
例3设H=2, 选取

则T3,T4都是e-不相干算子.

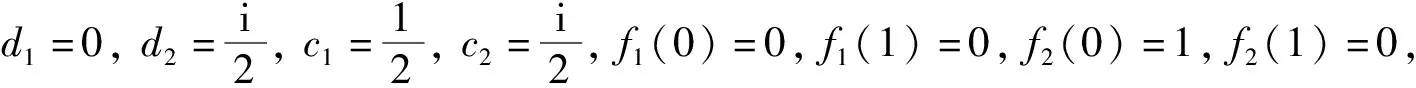
即存在ck,dk∈,f1,f2是从e到e的映射, 使得T3,T4有式(2)的形式, 从而由定理2可知,T3,T4都是e-不相干算子.由T3可见, 当Te某一列为0时能找到多个映射使其为式(2)的形式, 这与定理2必要性的证明中js的选取有关.

3 强不相干算子与严格不相干量子运算

定理3设H=2, 选取e={|0〉,|1〉}, 则σy=i|0〉〈1|-i|1〉〈0|是一个e-强不相干算子.

证明: 因为

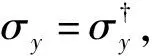
σy|0〉=(i|0〉〈1|-i|1〉〈0|)|0〉=-i|1〉,σy|1〉=(i|0〉〈1|-i|1〉〈0|)|1〉=i|0〉.

定理4设H=2, 选取e={|0〉,|1〉}, 对于任意的ρ∈D(2), 有

其中

则ε∉SIO(H),ε1∈SIO(H).

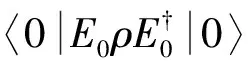
易得

同理可证

由定义4可知,ε1∈SIO(H).

推论1设T∈B(H), 则T为e-强不相干算子当且仅当Te的每行和每列都至多有一个非零元素.

注6对于定理3中的σy, 从形式上看σye的每行和每列都只有一个非零元素, 由推论1和定义2易知,σy是一个e-强不相干算子.

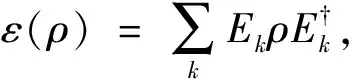
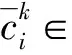
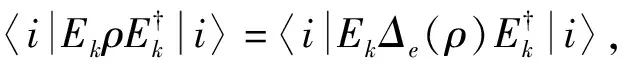
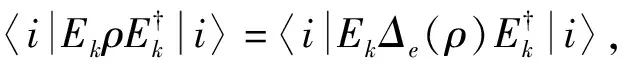
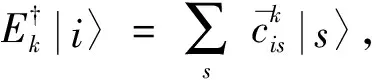
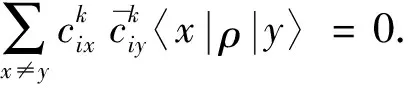
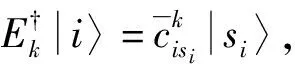
运用推论1, 能从一个算子的形式直观判断出它是否是强不相干算子, 进而通过定理5快速判断出其对应的量子运算是否是一个严格不相干量子运算, 从而为严格不相干量子运算的研究提供了方便快捷的方法.

例4对于定理4中的E0,E1,F0,F1, 从E0e,E1e的形式上看,E0e的第一行有两个非零元素,E1e的第二行有两个非零元素, 由推论1可知E0,E1都不是e-强不相干算子.因此{Ek}不是一组e-强不相干kraus算子.由定理5可知{Ek}对应的量子运算ε∉SIO(H).从F0e,F1e的形式上看,F0e和F1e的每行和每列都只有一个非零元素, 由推论1可知F0,F1都是e-强不相干算子, 因此{Fk}是一组e-强不相干kraus算子.从而由定理5可知{Fk}对应的量子运算ε1∈SIO(H).

注7因为SIO(H)是IO(H)的子集[14], 例2和定理4中的ε∈IO(H), 但ε∉SIO(H).因此SIO(H)是IO(H)的真子集, 即SIO(H)IO(H).

定理6设T∈B(H), 则T为e-强不相干算子当且仅当存在cx∈,π是从e到e的置换, 使得

(3)

证明: 充分性.设存在cx∈,π是从e到e的置换, 使得从而则

由注2可知,T是e-强不相干算子.

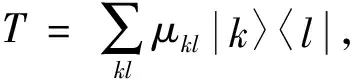
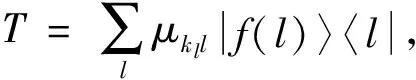
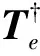
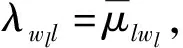
因此有

(4)

由式(4)可见, 当μkyy不全为0, 即|y〉∈e/{|l1〉,|l2〉,…,|ln〉}时, 则有: 当y=wl时,l=f(y)=ky=mwl=f(wl); 当y≠wl时,l=ky=f(y)≠kwl=f(wl).设e1={f(wl): |wl〉∈e/{|l1〉,|l2〉,…,|ln〉}}, 则易知f是从e/{|l1〉,|l2〉,…,|ln〉}到e1的双射.从而e/e1中有n个元素.

已知f(ls)=js,ls∈{|l1〉,|l2〉,…,|ln〉}.令js∈e/e1, 对于任意的|lt〉,|lr〉∈{|l1〉,|l2〉,…,|ln〉}, 当lt≠lr时, 有jt≠jr.从而此时f是从e到e的置换, 即π置换.令cl=μkll, 从而存在cl∈,π是从e到e的置换, 使得式(3)成立.

例5例3中的T3,T4都是e-强不相干算子.

证明: 由例3已知, 存在ck,dk∈,f1,f2是从e到e的映射, 使得

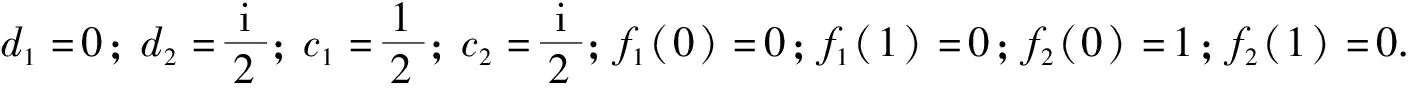
下面用定理5和定理6给出下列推论的另一种证明方法.

推论2[14]设{Ek}是量子运算ε的一组kraus算子分解, 则ε∈SIO(H)当且仅当存在ckx∈,πk是从e到e的置换, 使得Ek有以下形式:

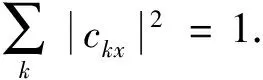
证明: 充分性.设{Ek}是ε的一组kraus算子分解, 则 存在ckx∈是从e到e的置换, 使得从而于是

因此ε是B(H)上的一个保迹完全正映射.由定理6可知,Ek是e-强不相干算子, 因此{Ek}是一组e-强不相干kraus算子.从而由定理5可知,ε∈SIO(H).

必要性.设ε∈SIO(H), 由定理5可知ε存在一组e-强不相干kraus算子分解{Ek}.因为Ek为e-强不相干算子, 所以由定理6可知, 存在ckx∈,πk是从e到e的置换, 使得由定义4可知,ε为一个保迹的完全正映射, 所以从而

综上所述, 本文用算子代数和矩阵论的方法对不相干算子和强不相干算子的特性进行了研究和讨论.首先, 给出了不相干算子的一些刻画及相应的不相干量子运算的结果; 然后给出了强不相干算子的一些刻画及相应的严格不相干量子运算的结果; 最后用实例验证了本文的结论.结果表明, 严格不相干量子运算是不相干量子运算的真子集.利用本文结果可更方便地判断一个算子是否是不相干的或强不相干的, 即从一个算子的形式可以直观判断出它是否是不相干算子或强不相干算子, 进而得出它对应的量子运算是否是不相干量子运算或严格不相干量子运算.这些结果不仅为不相干量子运算和严格不相干量子运算的研究提供了更方便快捷的方法, 而且对以后研究与不相干算子有联系的量子运算提供了更快捷简便的方法.例如, 真正不相干量子运算(GIO(H))[15]等.