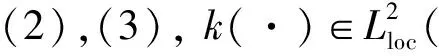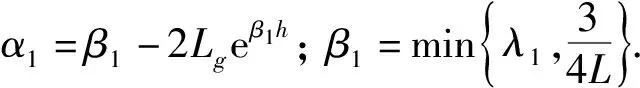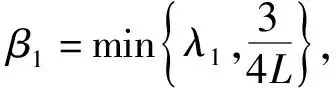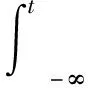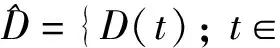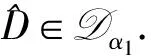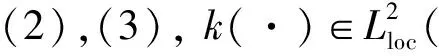带时滞非经典扩散方程依赖于时间的拉回吸引子
王芳平, 马巧珍
(西北师范大学 数学与统计学院, 兰州 730070)
0 引 言
设Ω⊂n(n≥3)是具有适当光滑边界∂Ω的有界区域, 本文考虑如下带时滞的非经典扩散方程解的渐近行为:
(1)
其中:τ∈;g是一个算子;k是依赖于时间的外力项;φ∈C([-h,0];Hτ)是初始值,h(>0)是时滞效果的长度; 并且对每个t≥τ, 用ut表示定义在[-h,0]上的函数ut(θ)=u(t+θ),θ∈[-h,0].
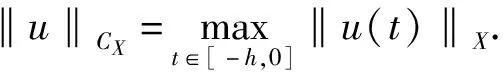
(H1)对所有的ξ∈CL2, 函数tg(t,·)∈L2是可测的;
(H2)对所有的t∈,g(t,0)=0;
(H3)存在Lg>0, 使得对所有的t∈和ξ,η∈CL2, 不等式‖g(t,ξ)-g(t,η)‖2≤Lg‖ξ-η‖CL2成立.
ε(t)∈C1()是关于t的有界减函数, 且满足下列条件:
(2)
特别地, 由条件(2)可知, 存在L>0, 使得
(3)
时间依赖吸引子的概念由文献[1-2]提出, 例如, 当波方程
ε(t)utt+αut-Δu+f(u)=g(x)
(4)
中的系数ε依赖于时间t时, 即使外力项不依赖于t, 系统仍是非自治的, 且其能量泛函也依赖于时间t, 即
当t→∞,ε(t)→0时, 系统的耗散性显然发生了改变, 并且在古典理论下得不到其耗散性.

目前, 关于偏微分方程时间依赖吸引子的存在性和正则性研究得到广泛关注, 如文献[2,10]系统地研究了波方程时间依赖吸引子的存在性、 渐近性及渐近结构; 文献[11-12]关于Plate方程分别得到了时间依赖全局吸引子和强拉回吸引子的存在性; 文献[13]获得了具有低正则性外力项的非经典扩散方程时间依赖全局吸引子的存在性及正则性结果; 文献[14]研究了非经典扩散方程时间依赖全局吸引子的存在性及其正则性.本文运用算子分解的方法并结合文献[8]的研究, 给出在非线性项满足多项式增长条件时依赖于时间的拉回吸引子的存在性.
1 预备知识
用(·,·)和‖·‖分别表示L2(Ω)中的内积和范数, 记H=L2(Ω).对于0≤σ≤2, 定义由A生成的空间族Hσ=dom(Aσ/2), 并赋予如下内积和范数:
(w,v)σ=〈Aσ/2w,Aσ/2v〉, ‖w‖σ=‖Aσ/2w‖.
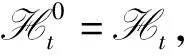

λ1‖v‖2≤‖v‖2, ∀v∈H1,
其中λ1是-Δ算子在Dirichlet边界条件下的的第一特征值.

定义1(拉回D-渐近紧)[8]如果对∀t∈,在X中是准紧的, 则称过程{U(t,τ)}t≥τ是拉回D渐近紧的.
定义2(拉回D-吸收集)[8]如果对∀t∈,存在τ0=τ0(t,D) 1)对所有的t∈, A(t)在X中是紧的; ‖U(t,t-T)x-U(t,t-T)y‖X≤ε+ψt,T(x,y), 其中ψt,T依赖于t和T.则{U(t,τ)}t≥τ在X中是拉回D-渐近紧的. ‖U(t,t-T)x-U(t,t-T)y‖X≤ε+ψt,T(x,y), 其中ψt,T依赖于t和T.则{U(t,τ)}t≥τ在X中是拉回D-渐近紧的. 定理3[9]设{U(t,τ)}t≥τ是Banach空间X上的一个过程.若其满足下列条件: 则{U(t,τ)}t≥τ在X中拥有拉回D-吸引子. (f(u)-f(v))(u-v)≤l(u-v)2, (5) (6) (7) 定义4对所有的T>τ, 方程(1)的弱解是函数u∈C([τ-h,T;Ht)∩L2(τ,T;H1)∩Lp(τ,T;Lp(Ω)), 其中对所有的t∈[τ-h,τ],u(t)=φ0(t-τ), 且对所有φ∈Ht, 在[τ,+∞)上满足 注1如果u(t)是方程(1)的弱解, 则对所有τ≤s≤t, 其满足能量方程 证明: 设{ωj}j≥1⊂H1∩Lp(Ω)是L2(Ω)的Hilbert基, 使得{ωj}j≥1在H1∩Lp(Ω)中是稠密的. (8) 下面分三步证明. 1)先验估计.由式(6)、 假设(H1)~(H3)及Hölder和Young不等式, 将方程(8)两边乘以νmj(t)后再从1到m求和, 使得对所有的t≥τ, 有 进而对几乎处处的t≥τ, 有 特别地, 对所有的t≥τ, 用t+θ代替t, 其中θ∈[-h,0], 得 (9) 对所有的t≥τ, 在[τ,t]上对式(9)积分得 由Gronwall引理知, 对所有的t≥τ,m≥n, 有 (10) 此外, 由假设(H1)~(H3)及Hölder和Young不等式, 使得对t≥τ, 有 (11) 在[τ,t]上对式(11)积分, 并由式(7)可知, 对所有的t≥τ, ∀m≥n, 有 (12) (13) 3)由稠密性证明一般情形.对每个n∈, 定义由于{ωj}j≥1是L2(Ω)的Hilbert基, 可知在CHt中φn→φ).初值且;L2(Ω))的方程(1)的解用un表示. 首先, 对每个满足能量方程的un, ∀t≥τ, 有 此外, 可改进上述收敛.考虑un和um的差, 并由un-um满足的能量方程, 可得对∀t≥τ, 有 (14) 用t+θ代替t, 其中θ∈[-h,0], 并由式(3)知, 对所有t≥τ, 有 (15) 对式(15)运用Gronwall引理得 将其代入式(14)知, 对所有的T≥τ, {un}在C([τ-h,T];Ht)∩L2(τ,T;H1)上是Cauchy列, 于是得到一个序列, 使得在Ω×(τ,∞)上un→u.综上并由文献[15]中定理1.3得X=f(u), 由满足方程的un的极限知u是方程(1)的弱解.证毕. 定理5在定理4的假设下, 方程(1)的弱解是唯一的.此外, 对 ∀t≥τ, 关于不同初值的两个解, 下列Lipschitz连续成立: (16) 其中:ω(t)∶=u1(t)-u2(t); 常数C=C(l,Lg). 证明: 函数ω(t)满足 (17) 用ω与式(17)做内积, 并运用式(5)和假设(H3), 得 特别地, 用t+θ代替t, 其中θ∈[-h,0], 得 由Gronwall引理得式(16).证毕. 对∀t≥τ, 在空间CHt中定义解过程如下: U(t,τ):CHτ→CHt,U(t,τ)φ(τ)=u(t), (18) 其中φ(τ)∈CHτ. 类似定理5的证明,有: 引理2假设条件(2),(3)及(5)~(7)成立, 则问题(1)生成的过程族U(t,τ):CHτ→CHt,t≥τ∈, 满足下列性质: 对∀t≥τ, 初值φi(τ)∈CHτ, ‖U(t,τ)φ1(τ)-U(t,τ)φ2(τ)‖Ht≤e2C(t-τ)‖φ1(τ)-φ2(τ)‖Hτ, 其中C=C(l,Lg). (19) 证明: 对方程(1)两边乘以u(t), 并在Ω上积分, 得 由式(6)、 假设(H3)及Hölder不等式, 得 即 由式(2),(3)得 (20) 因此 用t+θ代替t, 其中θ∈[-h,0], 得 (21) 用eβ1t乘式(21), 并在[τ,t]上积分, 对∀t≥τ, 得 (22) 则 由Gronwall引理, 得 (23) 其中β1-2Lgeβ1h=α1.将式(23)代入式(22)即完成证明. 为了得到拉回Dα1吸收集, 给出假设: 0<β1-2Lgeβ1h=α1, (24) 且对∀t∈, (25) (26) 同文献[8], 下面用收缩函数的方法证明由式(18)定义过程{U(t,τ)}t≥τ的依赖于时间的拉回Dα1吸引子的存在性. 定理7在引理3的假设下, 设{U(t,τ)}t≥τ是式(18)定义的过程, 则{U(t,τ)}t≥τ在CHt中是拉回Dα1-渐近紧的. 证明: 设ui(t)是关于初值φi(x,t)∈D1(i=1,2,θ∈[-h,0])的解, 即ui(t)是下列方程的解: ∂tu-ε(t)∂tΔu-Δu=f(u)+g(t,ut)+k(t), (x,t)∈Ω×[τ,∞), 初值 ui(x,τ+θ)=φi(x,θ),x∈Ω,θ∈[-h,0]. 为方便, 记ω(t)=u1(t)-u2(t), 则ω(t)满足方程 (27) 其中初值 ω(x,τ+θ)=φ1(x,θ)-φ2(x,θ),x∈Ω,θ∈[-h,0]. 用ω(t)乘式(27), 并在Ω上积分得 由式(20)及Poincaré不等式得 由Gronwall引理知, 对∀t≥τ, 有 运用Hölder不等式, 并注意到α1<β1, 用t+θ代替t, 其中θ∈[-h,0], 对∀t-h>τ, 得 令T=t-τ, 且 结合定义3、 引理4和式(19)知ψt,T是收缩函数, 于是对∀ε>0及取定的t∈, 设由定理1易得{U(t,τ)}t≥τ在CHt中是拉回Dα1-渐近紧的.证毕. 由定理7可得: 定理8在定理6的假设下, 设{U(t,τ)}t≥τ是式(18)定义的过程, 则{U(t,τ)}t≥τ在CHt中拥有唯一的拉回Dα1吸引子A1, 即关于CHt的范数拉回吸引CHt中的每个有界子集A1在CHt中是非空的、 紧的、 不变的.

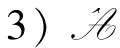
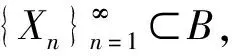



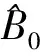
2 解的适定性
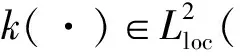
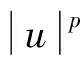

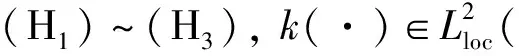
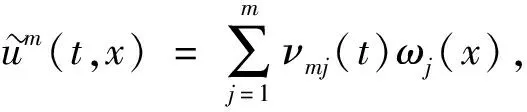
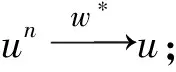
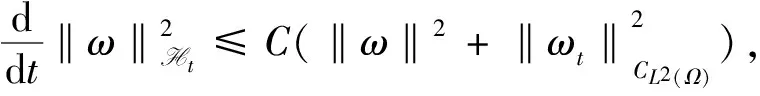
3 拉回吸引子