带积分边界条件的分数阶微分方程正解的存在性

何兴玥, 高承华

(西北师范大学 数学与统计学院, 兰州 730070)

0 引 言

分数阶微分方程在数学物理、 混沌与湍流、 化学物理、 空气动力学和非牛顿流体力学等领域应用广泛.与整数阶模型相比, 在很多情形下分数阶模型获得的数据更精确, 且有更多的自由度[1-2].因此, 近年来分数阶微分方程理论的研究得到广泛关注, 并已取得了许多结果[2-11].文献[4]用锥拉伸与压缩不动点定理研究了一类具有无穷区间参数的Riemann-Liouville分数阶微分方程正解的存在性；文献[5]用锥拉伸与压缩不动点定理和上下解的方法研究了一类分数阶微分方程初值问题解的存在性.特别地, 文献[6]用Guo-Krasnosel’skii不动点定理, 讨论了如下分数阶微分方程边值问题:

(1)

在超线性和次线性条件下正解的存在性, 其中: 2<α<3; 0<λ<2是参数.受文献[6]启发, 本文讨论如下非线性项和积分边值条件均带参数的非线性问题:

(2)

在不同增长条件下正解的存在性, 其中: 2<α<3;λ>0; 0<μ<2;f满足如下条件:

(H1)f∈C([0,1]×[0,∞),[0,∞)), 且f(u)>0,u>0.

1 预备知识

考虑线性问题:

(3)

引理1[6]假设y∈C[0,1], 则问题(3)有唯一解

(4)

其中G(t,s)是问题(3)的Green函数:

(5)

引理2[6]令2<α<3, 则G(t,s)有如下性质：

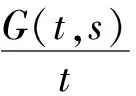
2)G(0,s)=G(t,1)=0,t,s∈[0,1],μ≠2;

3)G(1,s)=0,s∈[0,1),μ=0;G(1,s)>0,s∈(0,1),μ∈(0,2);

4)G(t,0)>0,t∈(0,1),μ∈[0,2);G(t,s)>0,t,s∈(0,1),μ∈[0,2);

引理3[6]令2<α<3, 0<μ<2,G(t,s)有如下性质：

(6)

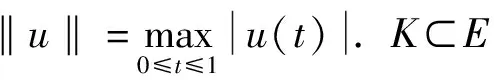
K={u∈E|u(t)≥0,u(t)≥ξσ‖u‖,t∈[ξ,1-ξ]},

(7)

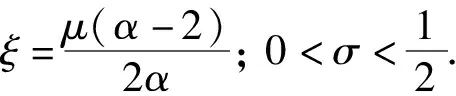
定义算子Tλ:C[0,1]→C[0,1]为

(8)

则由Arzela-Ascoli定理易证Tλ:K→K是全连续的.

定理1假设条件(H1)成立.若对任意的u∈K, 存在η>0, 使得f(t,u)≥ηu, 则

‖Tλu‖≥ληξσM‖u‖,t∈[0,1],

(9)

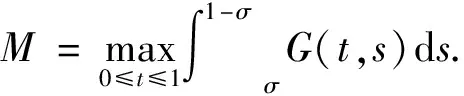
证明: 由Tλ和K的定义可得

定理2假设条件(H1)成立.若对任意的u∈K, 存在ε>0, 使得f(t,u)≤εu, 则

(10)

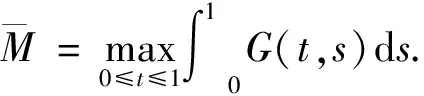
证明: 由Tλ和K的定义可得

令r>0, 定义

(11)

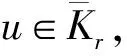
(12)

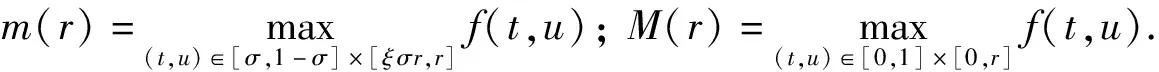
2 主要结果

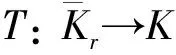
1)若‖Tx‖≥‖x‖,x∈∂Kr, 则i(T,Kr,K)=0;

2)若‖Tx‖≤‖x‖,x∈∂Kr, 则i(T,Kr,K)=1.

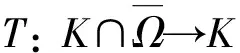
定义

定理4假设条件(H1)成立, 若f0∈[0,∞),f∞∈[0,∞), 且有

(13)

则问题(2)至少存在两个正解.

证明: 令r1=1, 则由定理3可得

(14)

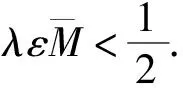
(15)

根据引理4, 有i(Tλ,Kr2,K)=1,i(Tλ,Kr1Kr2,K)=-1.

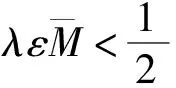
(16)

根据引理4有i(Tλ,Kr3,K)=1,i(Tλ,Kr1Kr3,K)=-1.于是由引理5可知Tλ至少存在两个正解.

定理5假设条件(H1)成立, 若f0∈[0,∞),f∞∈[0,∞), 且

(17)

则问题(2)至少存在两个正解.

证明: 令r1=1, 则由定理3可得

(18)

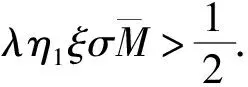
‖Tλu‖≥λ(f0-η1)ξσM‖u‖>‖u‖,u∈∂Kr2.

(19)

那个时候，唐飞霄曾对这些江湖上的传闻不屑一顾，然而如今，当看到自己那只精钢打造的节足，在天葬刀的刀锋下一掠而断的时候，他便知道，传言并非虚妄。

(20)

根据引理4有i(Tλ,Kr3,K)=0,i(Tλ,Kr1Kr3,K)=1.于是由引理5可知Tλ至少存在两个正解.

定理6假设条件(H1)成立, 若f0∈(0,∞),f∞∈(0,∞),f0∈(0,∞),f∞∈(0,∞), 则

(21)

或者

(22)

成立时, 问题(2)至少存在一个正解.

证明: 只考虑情形(21), 另一种情形可类似证明.取ε>0满足

(23)

由f0的定义, 存在实数r1>0满足f(t,u)≤(f0+ε)u,u∈[0,r1].由引理2可得

(24)

于是由引理4可知i(Tλ,Kr1,K)=1.

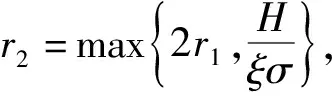
(25)

定理7假设条件(H1)成立.

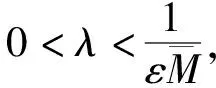
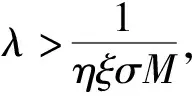
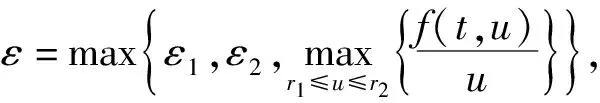
(26)

矛盾.因此, 问题(2)不存在正解.

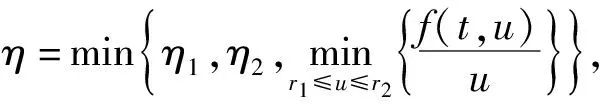
‖v‖=‖Tλv‖≥ληξσM‖v‖>‖v‖，

(27)

矛盾.因此, 问题(2)不存在正解.

3 应用实例

下面分别取不同的且分别满足定理4、 定理6和定理7条件的函数f, 给出满足问题(2)正解的存在性和不存在性结论的实例.

例1考虑问题(2).

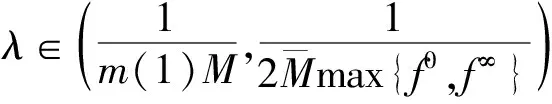
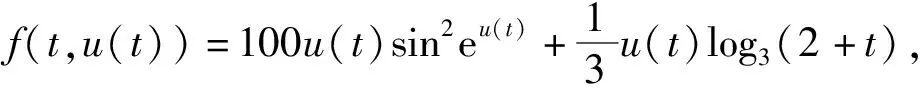
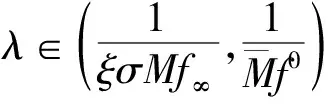
情形3)若f(t,u(t))=u(t)(sin2eu(t)+tln(1+cosu(t))).