基于盾构隧道环缝点云的中轴线提取方法

陈 林,葛坤龙,王 涛

(苏州工业园区测绘地理信息有限公司,江苏 苏州 215000)

传统基于点云的隧道断面变形监测方法通常首先是要提取隧道的中轴线,即隧道断面中心的连线,并以此为基准分析隧道连续断面的收敛及沉降,因此中轴线的提取方法和精度对后续的变形分析至关重要[1-2]。国内外学者对此已进行了一定的研究:2013年,托雷等[3]利用RNASAC算法拟合了地铁隧道中轴线并实现隧道断面的截取与曲线拟合;2014年,Fekete等[4]提出基于圆柱面拟合的隧道中轴线提取方法;2015年,李双[5]提出了基于三维不变矩的局部隧道中轴线提取方法。上述方法在三维空间内实现较为繁琐,尤其是针对运营期的隧道,大量管线设备安装在隧道壁上,导致需要进行大量的点云预处理工作。

盾构隧道拥有独特的结构形式,图1为盾构隧道管片安装结构展开图。其中,管片左右间空隙为环缝,上下间空隙为纵缝,拼接空隙可以看做是隧道中的“合理裂缝”[6-7]。随着地面LiDAR(激光雷达)技术和图像处理技术的发展,非接触、高精度的三维裂缝检测与分析成为可能,而且相比于隧道混凝土表面的细小裂缝而言,管片拼接空隙更容易被激光识别[8]。本文以地面LiDAR技术获取的盾构隧道点云数据为对象,顾及盾构隧道预制管片拼接的特点,引入裂缝识别与提取方法[9-10],以隧道管片拼接环缝为边界对点云数据分块,通过拟合边界曲线来间接提取隧道中轴线。

1 基于距离差特征的管片拼接环缝点云分析

图2为隧道管片环缝处点云的剖面示意图。可以看出,A1、A2、A7和A8这4个点处在隧道面上,而A3、A4、A5和A6这4个点偏离了隧道面,且与隧道面的距离值大致呈凸状,被视作裂缝内的离散点[11]。

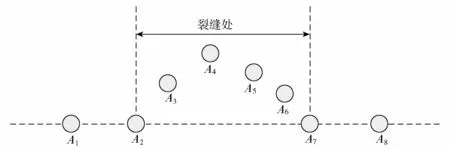
图2 基于距离差的裂缝结构描述Fig.2 Description of fracture structure based on the distance difference feature

根据上述基于距离差的裂缝结构描述,对裂缝的属性变化和变化规律进行分析。从左至右,假设各离散点到隧道面的距离为D(Ai)i=1,2,…,8。其中,A1点和A2点同处在隧道面上,理论上到隧道面的距离相等,但由于地面LiDAR测距误差的存在,D(A1)和D(A2)之间会存在一个差值α2,如式(1)所示。由于这个差值的存在导致基于距离差特征的环缝需要确定一个阈值。

|D(A2)-D(A1)|=|α2|

(1)

从左至右依次将离散点到隧道面的距离为D(Ai)i=1,2,…,8与D(A1)作差:

|D(Ai)-D(A1)|=|αi|

(2)

由图2可以看出,环缝内各离散点到隧道面的距离与A1点到隧道面距离的差值|α3|、|α4|、|α5|和|α6|明显大于|α2|。若能找到一个阈值δ(δ≥0),对由误差产生的距离差和环缝点与隧道面上点的距离差加以区分,即可实现对环缝点的提取。

从上述关于距离差特征的隧道环缝点云分析可知,若在隧道面上确定一点,并求出该点到隧道面的距离D,自该点沿某一方向遍历点云,当某个离散点到隧道面的距离Di与D的差值超过阈值δ时,表明该点的前一个点为环缝起点,随着点云在该方向上的前进,后续的离散点到墙面的距离与D的差值会慢慢增大,到达一个最大点后再慢慢减小直至小于阈值δ,表明裂缝结束,由此可提取出完整的环缝处点云。

图3 盾构隧道点云图Fig.3 Point cloud of shield tunnel

2 盾构隧道点云中轴线提取

由第1节中基于距离差的环缝特征分析可知,各离散点到隧道面距离的差值是判断该点是否为裂缝点的重要依据。因此,首先需要通过点云来拟合隧道面的方程,再通过点到平面的距离公式来提取裂缝点。但是由于隧道面是一个圆柱面,拟合方程较为复杂,因此考虑以单测站上同一高度(即Z坐标值相同)点云拟合曲线方程,并通过各点到曲线的距离来识别裂缝点。

2.1 同一高度点云选取

地铁隧道形变监测工作很大一部分是处在地铁运营期。图3为运

营隧道点云图,由于各种管线设备的阻挡,难以获得完整的隧道内壁点云图,使得点云图上存在很多空洞;另一方面,隧道管片上存在很多孔洞,导致隧道内壁不够平滑。基于这两方面,若直接对隧道进行同一高度点云提取必然存在很大的问题。因此,需要先在点云可视化软件中选取隧道点云平滑无孔洞并完整的区域,再展开提取工作。

地面LiDAR系统激光照射在目标物上形成的光斑虽然微小,但还是存在一定的半径,若指定Z坐标初始值z0i(i表示选定的第i个初始值)对离散点云进行索引,则提取出的点云数量会很少。因此考虑以垂直方向的扫描间隔Δt为阈值,索引区间[z0i-Δt,z0i+Δt]内的所有点。

2.2 基于最小二乘法的线性拟合

从2.1节中关于激光光斑的阐述可知,选取隧道点云同一高度上的一系列离散点应当是分布在某一曲线的两侧,因此无法直接确定曲线方程,需要通过拟合来进行求解。

参考隧道扫描坐标系的建立并结合实际可知,由于Z坐标近似,因此只需要在XOY面进行线性方程拟合[12-13]。

假设拟合的线性方程为

y=kx+c

(3)

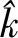
(4)

组成法方程,有

(5)

2.3 管片环缝点判别

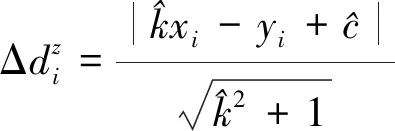
(6)

结合第1节中基于距离差特征的环缝点云分析,对各离散点到直线(即隧道面)的距离差值进行比较,识别出裂缝处点云。

2.4 基于最小二乘法的环缝断面圆曲线拟合

测站隧道扫描坐标系下,管片环缝断面与隧道中轴线垂直,即Y坐标一致,因此只需要考虑XOZ平面内圆曲线的拟合。盾构隧道的弯曲部分通常呈圆弧状,因此用圆曲线方程来拟合[14-15]。本文利用基于圆半径距离差的最小二乘法来对圆曲线进行拟合,同样是在XOY平面内进行。

设隧道管片纵缝处断面的圆曲线方程为

(x-a)2+(y-b)2=R2

(7)

式中:(a,b)——圆心坐标;R——圆半径。

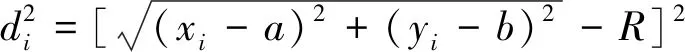
(8)

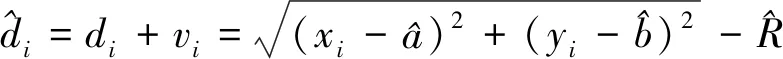
(9)

将式(9)按Tylor公式展开,得

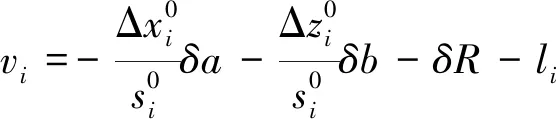
(10)

若将式(10)用矩阵的形式表达,即

(11)

根据间接平差原理可知:

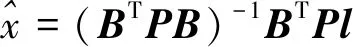
(12)

式中:P——权阵,由于离散点云相互独立且精度相当,故P为单位阵,即P=I,所以可将式(12)简化为

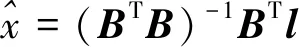
(13)

拟合出来的圆曲线即为隧道环缝断面的位置所在。

2.5 基于管片环缝断面的隧道中轴线提取

提取中轴线的意义在于可以确定隧道点云的空间姿态。同时,对于圆柱面外观的盾构隧道而言,中轴线相当于圆柱的轴线,轴线确定后,圆柱的半径就不难求出,这会为后续的隧道收敛形变分析提供很大的便捷。在拟合出环缝断面曲线的基础上进行中轴线提取,具体步骤如下:(a)根据中间环片两侧环缝断面曲线方程及其在Y轴上对应的位置范围,提取出中间环片的点云,实现环片分离。(b)环片分离后,单环片两侧圆曲线圆心位置的连线即为隧道的中轴线。

3 实验与分析

由于单测站获取的点云数量较大,因此只截取其中部分点云作为研究对象。图4为截取出来的原始点云,点云中包含3个完整的隧道环片,以此为对象研究中间环片两侧环缝的提取。

3.1 隧道断面环缝提取实验

根据2.1节在点云可视化软件上寻找平滑无孔洞区域共计6块。图5(a)为利用其中一块区域根据2.2节拟合出来的直线方程,选取初值z01=2.322 3 m,按阈值垂直扫描间隔Δt=0.5 mm,在索引区间内共提取出437个点,考虑到显示问题,仅随机选取了其中1/20点加以显示。图5(b)为以点到直线的距离为Y轴、各离散点Y坐标为X轴绘制的437个离散点的变化折线,可以明显看出2个环缝所在的位置。

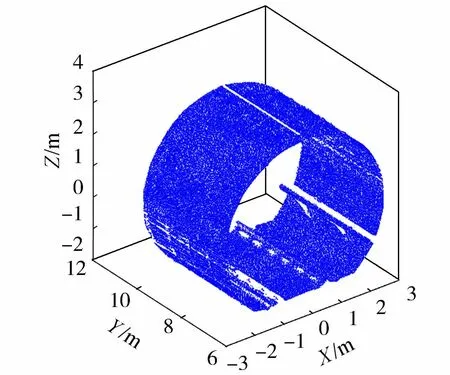
图4 原始点云图Fig.4 Original point cloud

图5 拟合效果Fig.5 Effect of linear fitting

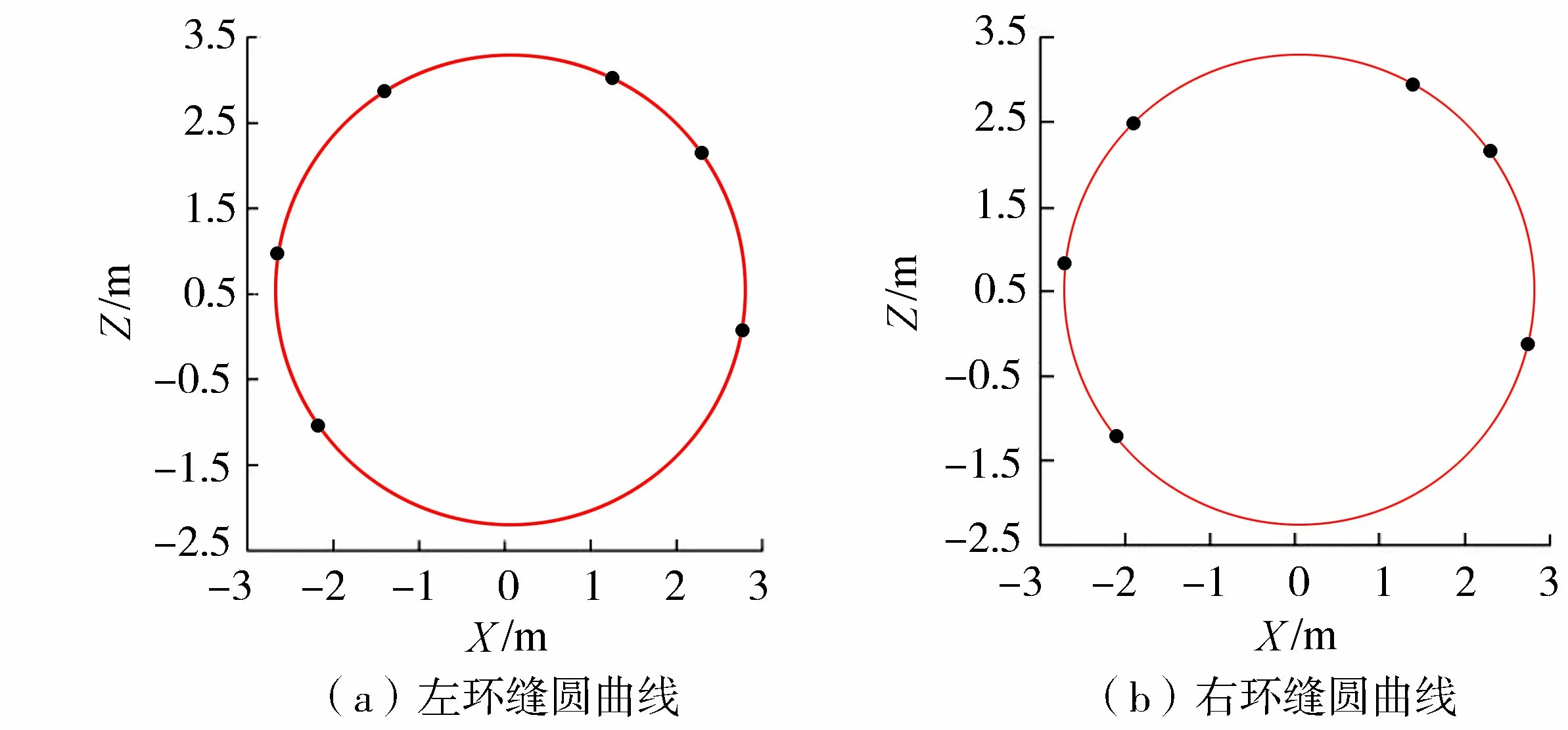
图6 曲线拟合效果Fig.6 Effect of curve fitting

图6是根据2.4节拟合出来的中间环片两侧环缝的圆曲线。其中,图6(a)为中间环片左侧环缝圆曲线,圆心坐标为(0.065 9,0.524 1),半径为2.763 3 m,Y轴上的坐标为7.673 4 m;图6(b)为中间环片右侧环缝圆曲线,圆心坐标为(0.065 9,0.524 3),半径为2.763 3 m,Y轴上的坐标为8.892 1 m。

3.2 中轴线提取实验

如图7(a)所示,红色曲线为根据环缝拟合出来的圆曲线,按图中红色曲线位置将原始点云切开即可实现单环片分离。如图7(b)所示,黑色圆为两侧圆曲线的圆心所在位置,红色直线即为中轴线。

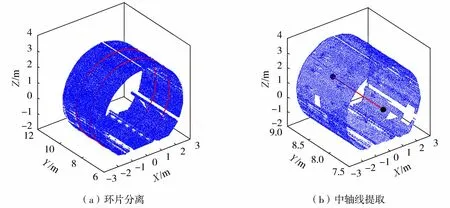
图7 隧道单环片中轴线提取效果Fig.7 Central axis extraction of tunnel ring

由3.1节与3.2节的盾构隧道环缝及中轴线提取实验可知,基于特征点云提取的方法,依靠点云可视化软件的辅助,有效减少了点云预处理的工作量,而传统的三维不变矩法[2]以及圆柱面拟合法[3]受限于隧道内部类似管线点云等噪声对中轴线提取精度的影响。同时,该方法直接应用于三维空间内的隧道点云,相较于投影拟合法[1]提取的隧道中轴线更具有空间意义。

4 结 语

在总结现有基于点云的隧道中轴线提取方法的基础上,从点云特征提取方面入手,研究了基于特征点云提取的盾构隧道环片分离与中轴线提取方法。该方法以环缝位置为参考,将隧道整体点云局部化,有效避免了隧道整体点云分析存在的数据量大、不易处理以及点云情况多样等问题,同时对环片分别进行分析,使得后续的隧道形变提取更易进行。

盾构隧道存在曲线部分,本文使用的方法仅适用于直线部分。考虑到盾构隧道弯曲部分在施工过程中参照的曲线方程不一致,因此无法以统一的曲线方程进行环缝点识别,因此今后还需进一步对隧道曲线位置环缝点的识别与提取进行研究。此外,盾构隧道环缝本身也存在着错位等复杂情况,本文基于距离差的环缝提取方法适用于较为理想的情况,因此提出一种能够识别各种情况裂缝的方法也是后续研究的方向和难点。