DRAINMOD和HYDRUS-1D模型对水稻控制灌排条件下农田水位的模拟
俞双恩,李倩倩,陈凯文,张梦婷,王 梅,王 煜,刘子鑫
(河海大学农业工程学院,江苏 南京 210098)
水稻是我国三大粮食作物之一。作为世界上重要的水稻生产国,我国水稻种植面积占耕地总面积的26%[1-2],但稻作区灌溉用水量占农业用水量的70%[3],水资源短缺已成为水稻生产的重要制约因素。水稻种植区主要分布在雨水充沛的湿润地区,其生长期与各地汛期重合。为了充分利用天然降雨,俞双恩等[4]将节水灌溉与控制排水技术有机结合,形成了以稻田水位作为灌排控制指标的水稻控制灌排技术。控制灌排技术作为南方稻作区的核心灌排技术,综合考虑了节水灌溉与控制排水的协同效应,对实现稻作区的节水、减排、控污、高产具有重要意义[5-7]。
HYDRUS-1D模型是由美国国家盐分实验室(US-Salinity Laboratory)研发的土壤水、热及溶质运移数值模拟软件。近年来,HYDRUS-1D在农田水分运移模拟方面应用较广。张海阔等[8]通过比较分析HYDRUS-1D 输出变量土水势和累积入渗量,探讨了变水头入渗条件下 VG 模型参数的敏感性;赖晓明等[9]应用HYDRUS-1D模型模拟太湖流域的农田水分渗漏规律,分析了太湖流域农田氮磷流失特征;Li等[10]利用HYDRUS-1D模拟在水稻直播情况下,稻田中氮磷运移规律,分析评价农田水氮平衡。但是将HYDRUS-1D模型应用于干湿交替的稻田水分模拟不多见。另外,20世纪70年代末由Skaggs[11]开发的DRAINMOD模型广泛应用于农田排水的理论分析和工程设计,可以较准确地预测田间地下水位、地表和地下排水量及作物产量等[12-13]。2006年,罗纨等[14]将 DRAINMOD模型应用于水稻灌区,模拟了宁夏银南灌区稻田排水过程;2011年,高学睿等[15]研究了DRAINMOD-NⅡ模型在气候湿润的南方水稻灌区的适用性,模拟了湖北漳河灌区排水和氮素流失规律,认为该模型可有效地模拟预测水稻田排水特性及氮素运移特性;王宁等[16]利用 DRAINMOD-NⅡ模型模拟了暴雨后稻田排水量及其氮素流失规律。前人对于DRAINMOD模型在水稻田的应用研究多基于常规灌排模式,但对于控制灌排条件下水稻田的应用研究鲜有报道。
综上,DRAINMOD模型和HYDRUS-1D模型在控制灌排条件下水稻田应用较少,本文利用这2个模型对试验区农田水位进行模拟研究,探讨它们在水稻控制灌排模式下的适用性,旨在为水稻控制灌排条件下农田水分运移模拟和研究提供方便可行的方法。
1 材料与方法
1.1 试验区基本情况
试验分别于2017年和2018年的5—10月在河海大学南方地区高效灌排与农业水土环境教育部重点实验室节水园区内进行。试验区(31°54′N,118°46′E)属于亚热带湿润性气候,多年平均降雨天数为120 d,多年平均降雨量1 072.9 mm。该地区多年平均日照时数2 017.2 h,多年平均蒸发量900 mm,多年平均无霜期224 d,年平均气温15.7℃。试验区内设有32个固定式蒸渗测坑(有底28个,无底4个),每个蒸渗测坑的规格为2.5 m×2 m×2 m(长×宽×高),按南北方向布置,共2排,每排16个,试验区布置见图1。地下设有廊道和设备间,地上设有移动式雨棚。测坑内土壤为黏壤土,全氮、速效氮、全磷、速效磷质量比分别为0.91 g/kg、27.65 mg/kg、0.32 g/kg、12.5 mg/kg。土壤的物理性质指标见表1。

图1 试验区平面布置示意图Fig.1 Schematic diagram of plane layout of the study area
1.2 试验设计
供试的水稻品种为南粳9108。2017年,水稻于5月29日育秧,6月29日移栽,10月27日收割。2018年,水稻于5月27日育秧,6月27日移栽,10月23日收割。水稻控制灌排处理设置3个重复,农田水位指标如下:分蘖期、拔节孕穗期、抽穗开花期、乳熟期的灌水适宜下限值分别为-20 cm、-30 cm、-20 cm、-30 cm,灌水适宜上限皆为3 cm,降雨时允许蓄水深度分别为10 cm、15 cm、15 cm、15 cm。农田水位调控值以田面为基准,正值表示地表水层深度,负值表示田间地下水埋深。黄熟期遇雨排水、自然落干。试验以农田水位为控制指标,当稻田水位超过蓄水上限时,采用抽水泵排水至蓄水上限,然后自然耗干田面水层直到地下水埋深达到设定的灌水下限值后立即灌至田间适宜水层。田面有水层时,保持2 mm/d的田间渗漏量;田面无水层时,控制渗漏量为0 mm/d。
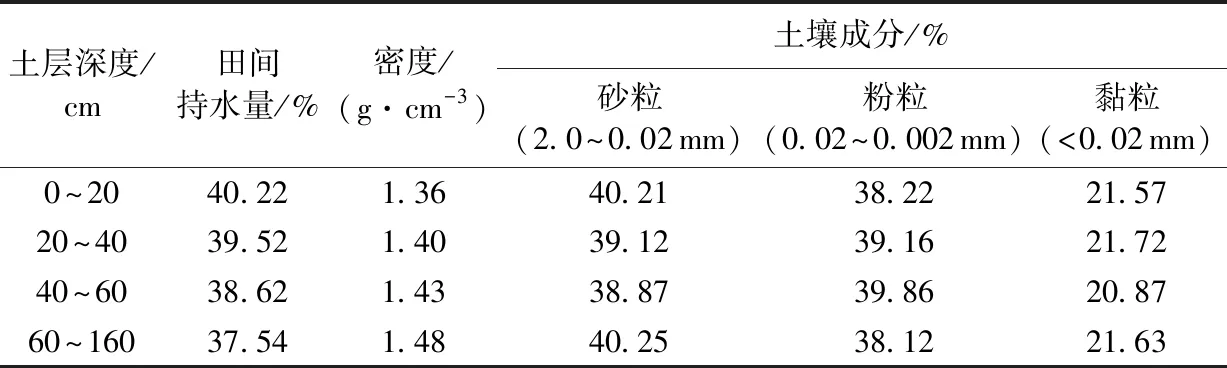
表1 供试土壤的主要理化性质指标
1.3 试验观测
a. 气象资料:节水园区内气象站观测的气象要素,包括降水量、最高温度、最低温度、相对湿度、风速、日照时长、辐射等,缺省值来自于中国气象科学数据共享服务网(http://data.cma.cn/)提供的南京(StationID:58238)气象数据。
b. 农田水位:在距离蒸渗测坑边缘50 cm处埋设由PVC管制成的地下水位观测井,每天7:00~8:00定时观测水位。以测坑内土壤表面为基准点观测农田水位:基准点以上为正,表示田面积水深度;基准点以下为负,表示田间地下水埋深。
c. 株高:每个蒸渗测坑设置6个观测点,从水稻移栽之日起,每5 d在固定观测点观测水稻株高的动态变化情况,测量作物地面以上的长度作为株高,不包括根部;扬花之前测量测坑地面线至最高叶尖的高度,扬花后测量稻田地面线至穗顶(不计芒)的高度。
d. 叶面积指数LAI: 每5 d使用LAI-2000叶面积仪(LI-COR,USA)定时观测水稻群体LAI。
2 模 型 建 立
2.1 模型原理
2.1.1 DRAINMOD模型原理
DRAINMOD模型是一个田间水文模型[11],适用于地下水位较高的情况,用来模拟农业水管理对农田的水文效应以及对作物产量的影响。DRAINMOD水文模型以土壤剖面水量平衡原理为基础[17],在时间增量Δt内,土壤剖面的水量平衡方程[18]可表示为
ΔVa=DS+ET-I
(1)
式中:ΔVa——土壤中的水量变化;ET——作物腾发量;DS——渗流量,包括深层渗漏量和侧向排水量;I——入渗量。
土壤表面的水量平衡方程可表示为
ΔS=P-I-R
(2)
式中:ΔS——土壤表面蓄水变化量;P——降水量;R——地表排水径流量。
2.1.2HYDRUS-1D模型原理
HYDRUS-1D模型利用一维Richards方程描述饱和-非饱和土壤水运动,并考虑了植物根系吸水,适用于各种恒定或非恒定的边界条件[18]。不考虑土壤水的水平运动,只考虑一维垂向运移,含根系吸水源汇项的土壤水分运动Richards方程为
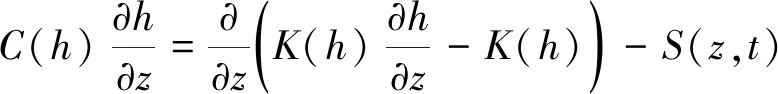
(3)
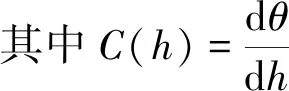
式中:C(h)——比水容量,cm-1;θ——土壤体积含水率,cm3/cm2;h——压力水头,cm;K(h)——非饱和导水率,cm/d;S(z,t)——t时刻z深度处耗水速率,取该处作物根系吸水率,cm3/(cm3·d)。
2.2 模型参数输入
2.2.1 气象资料
模型中需要输入的气象资料包括降雨量(将灌溉量转化为降雨量)和潜在蒸发蒸腾量及日最高、最低气温。潜在蒸发蒸腾量是由HYDRUS-1D模型中的Penman-Montheith公式计算得到的。
2.2.2 土壤参数
试验区土壤为黏壤土,将0~160 cm土层分为4层,各层土壤的组成成分见表1。采用RETC软件根据土壤粒径分级(砂粒、粉粒和黏粒的质量分数)和土壤干密度数据反演获得模拟所需的土壤水力特性参数的初始值[19-20],模型原理见文献[20]。利用2017年实测水位数据对土壤水分运动模型进行率定,率定过的土壤水力特性参数见表2。

表2 土壤水力特性参数
注:θr为土壤残余含水率,θs为土壤饱和含水率,α、n分别为土壤水分特征曲线统计参数,Ks为土壤饱和导水率,l为土壤孔径连通系数,Kls为土壤侧向饱和导水率。
2.2.3 作物参数
作物参数包括作物有效根深、株高及叶面积指数,取2017年和2018年试验观测得到数据的平均值作为水稻作物参数输入模型。
2.2.4 模型其他参数
除土壤参数和气象资料外,DRAINMOD模型还需输入排水参数。杨琳等[21]在探讨暗管控制排水对地下水位的调控作用时,对测坑的边界条件进行概化,将DRAINMOD模型应用于测坑尺度,并取得较好的模拟效果。在蒸渗测坑中,距地表150 cm深度处埋设有效半径2 cm的集水管,用于收集渗漏水,因此,将集水管概化为有效半径2 cm、埋深150 cm、间距200 cm的暗管排水系统,排水系数为0.2 cm/d,Kirkham积水深度为3 cm。
HYDRUS-1D模型需要确定其定解条件。水稻插秧时地表有水层,初始时刻分别实测地表淹水深度及底部测压管水头,经过线性插值得到土壤剖面水头分布,以此作为初始条件。上边界条件采用有表层积水的大气边界条件,最大积水深度分蘖期为10 cm,其他生育期为15 cm。当降水量超过地表最大积水深度时将产生地表径流。在模拟时段,逐日输入上边界通量值,包括降雨量(将灌溉量转化为降水量)和潜在蒸发蒸腾量。下边界条件采用时变通量边界条件,逐日输入蒸渗测坑底部的实测排水量。
2.3 模型的评价标准

3 模拟结果及分析
3.1 模拟结果
采用2017年7—9月期间的农田水位对模型进行参数率定,采用2018年7—9月期间的农田水位进行模型验证,对比分析2个模型在干湿交替的控制灌排模式下的适用性。2017年和2018年农田水位观测值与模拟值见图2,地表积水深度的观测值与模拟值见图3。根据实测值与模拟值计算评价2个模型模拟效果的指标(表3)。
图2给出了2017—2018年控制灌排条件下农田水位观测值与模拟值之间的对比。从图2中可以看出,观测到的农田水位与模型模拟结果之间吻合较好,模拟结果能较好地反映实际情况。从图3可以看出,测坑内稻田积水深度散点都较好地集中在 1∶1 直线附近,表明2个模型在模拟稻田积水深度时具有较好的适用性。
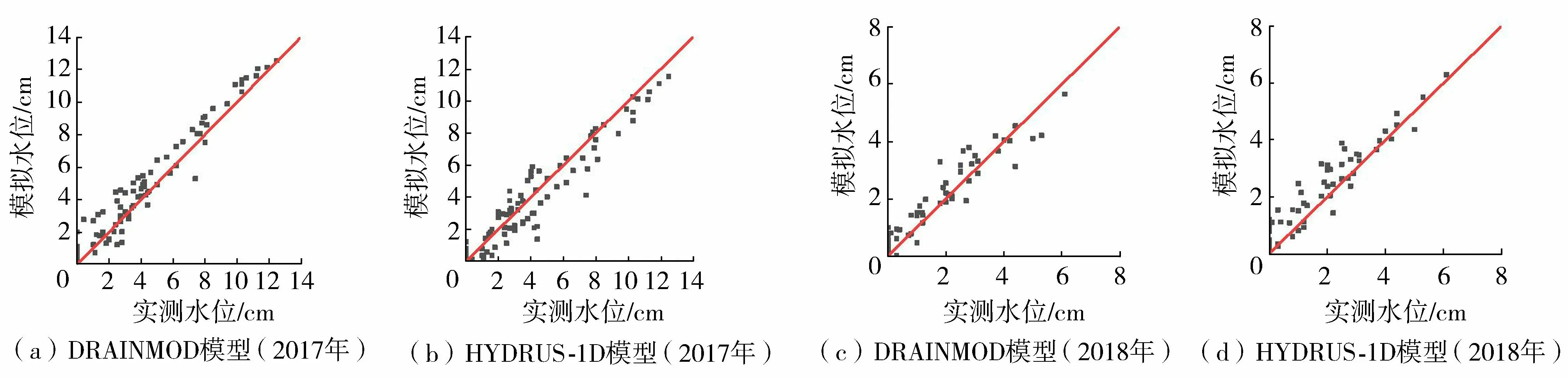
图3 地表积水深度散点图Fig.3 Scatter diagram of the layer depth of surface water

模拟年份观测变量DRAINMOD模型HYDRUS-1D模型Rδ/cmNSRδ/cmNS20172018地表积水深度0.977 -0.4130.9300.9730.3650.930农田水位0.9040.8160.7200.8882.1620.378地表积水深度0.959-0.1160.9130.959-0.2470.881农田水位0.7782.0510.5090.8491.8090.360


3.2 模拟结果讨论
a. DRAINMOD模型和HYDRUS-1D模型在模拟计算中,采用的土壤水力特性参数是根据土壤颗粒级配和干密度反演得到的,可能与实际的土壤物理性质存在一定出入。此外,气象条件和土壤条件在实际中也存在较大空间变异性,观测数据质量的好坏能直接影响模拟质量的好坏,这些是导致模拟误差偏大的原因之一。由图2可以看出,当地表无积水(农田水位小于0)时,模拟值与实测值之间存在较大偏差。王少丽[23]认为可能是因为在地下水位较浅时,土壤水力学特性对地下水位的预测比较敏感,因此,在这个时期模拟的水位波动较大,可能会产生大的误差。也可能是由于稻田土壤的包气带存在饱和与非饱和频繁交替的情况,土壤处于反复脱湿与吸湿的过程,而土壤水分特征曲线存在滞后效应,干湿交替条件下描述稻田土壤水分运移的VG模型参数会发生变化,因此,农田水位波动频繁、变幅较大,可能会对模拟精度产生影响。总体而言,DRAINMOD模型和HYDRUS-1D模型能够很好地适应试验区以农田水位为控制指标的灌排模式。
b. 根据表3中的模拟效果评价结果,可以认为本文中对于排水系统的概化是合理的,即可以将测坑中埋设的集水管概化为相同埋深的以测坑宽度为间距的排水暗管,通过概化可将DRAINMOD模型应用于测坑尺度下农田水分运动的模拟研究,以分析稻田水分运动规律。
c. HYDRUS-1D模型采用有限单元法经过反复迭代求解。在模型模拟过程中,最大迭代步长能较为明显地影响模拟结果,而土层网格的密度划分影响模拟结果的精度。关于迭代步长的设置和土层网格密度的划分对HYDRUS-1D模型模拟结果的影响机理还需进一步探讨。
4 结 语
将DRAINMOD排水模型和HYDRUS-1D模型应用于水稻控制灌排蒸渗测坑试验的农田水位模拟,采用2017年试验观测数据进行参数率定、2018年数据对模型进行验证,通过农田水位的模拟值与实测值比较,分析控制灌排条件下2个模型在稻田水分运移模拟研究中的实用性。确定了模型运行所需的参数设置和概化方法,并以相关系数、平均偏差及纳什效率系数为评价指标,检验农田水位模拟值与实测值的吻合程度,分析模型的可靠性。结果表明,DRAINMOD模型和HYDRUS-1D模型均可用于模拟控制灌排条件下稻田的水分运移,模型模拟结果较好地反映了水稻控制灌排条件下农田水位的变化情况,为稻田水分管理提供方便可行的方法。

