基于PSO与K-均值聚类算法优化结合的图像分割方法

曹帅帅，陈雪鑫，苗 圃，卜庆凯

(青岛大学电子信息学院，山东 青岛 266071)

0 引 言

图像分割是根据图像的不同特征划分为不同的区域并提取出感兴趣的区域。图像分割是在保留图像相关特征的基础上，将图像空间的对象目标分成若干个有效区域，有利于减少在后续分析和处理数据的工作量，提高图像处理的效率[1-2]。

许多学者引进新的方法和思想不断完善图像分割的领域，凭借聚类技术的出现为图像分割方法提供了更多可能。MacQueen[3]在1967年提出了K-均值聚类算法(K-means clustering algorithm)，K-均值聚类算法是到目前为止应用最广泛最成熟的一种聚类分析算法，具有高效性、可伸缩性和局部寻优能力强的特点，它适用于数据挖掘，同时也适用于图像处理领域。李光等[4]提出了一种基于K-均值聚类与区域合并的彩色分割方法，有效地提高了自然彩色图像的分割效果。赵丽[5]通过结合图像空间信息，将K-均值聚类算法用于含有噪声的图像分割，加强了K-均值算法在复杂环境中的图像分割能力。但是，K-均值算法对初始聚类中心选取要求很高而且容易收敛到局部最优解从而错过全局最优解。鉴于K-均值算法存在的缺陷，研究人员对其进行了改进优化。Kennedy和Eberhart在1995年提出了粒子群优化(Particle Swarm Optimization， PSO)算法，PSO算法拥有强大的全局寻优能力，适当优化惯性权重可以增强全局搜寻能力。李凯等[6]提出了一种粒子群优化算法和K-means聚类算法混合的棉花叶片图像分割方法。夏奇等[7]将PSO与K-means算法结合应用在组合导航中。Zhang等[8]提出了一种适用于多目标粒子群优化算法，通过调整粒子群权重系数等参数，实现算法的快速收敛。将全局寻优能力强大的PSO算法与局部寻优能力强大的K-均值算法如何有效地强强联合并且应用于图像分割方面，是众多学者研究的方向。

本文受PSO算法权重系数的启发，对传统固定值惯性权重做出改变的同时调整学习因子做辅助，改善PSO算法过早收敛到局部最小值的弊端。在后期，以合适的粒子适应度切换至K-均值算法完成图像分割，可以获得更有效的结果。

1 HSV颜色空间

图1 HSV颜色空间模型

已有设备输出的图像以RGB(Red、Green、Blue)颜色模型为基础，每种颜色出现在红、绿、蓝的原色光谱分量中，但在此模型中3个颜色分量之间存在高度相关性[9-11]。RGB颜色空间并不能满足人对颜色的感知，而且，在RGB颜色空间2个颜色点之间的距离并不能完美地表示出知觉之间的差异。HSV(Hue、Saturation、Value)颜色模型更接近于人们的经验和对彩色的感知，故采用HSV颜色空间来实现分割空间的选择。其中，H代表色调，S代表饱和度，V代表亮度值。分别采用二维卷积滤波进行去噪预处理，将去噪处理后的H、S、V分量通道三色图重组得到预处理后的图像，HSV彩色空间通过沿灰度轴研究RGB彩色立方体加以公式化，得出图1所示的六边形彩色调色板。

RGB颜色空间转换到HSV颜色空间公式如下：

(1)

(2)

V=max

(3)

其中,max=max(R,G,B)，min=min(R,G,B)。H的取值范围为0°～360°，S值和V值的范围为0～1。

2 K-均值算法

使用聚类算法完成图像分割，首先用特征向量的形式表示对应的图像空间中的像素点，然后借助特征向量的相似性划分为不同的种类[12-13]，最后将其映射回原图像空间，完成图像分割。

K-均值算法能够使聚类域中所有样本到聚类中心距离的平方和最小[14]。在整体样本数据中选取k个初始聚类中心，计算每个样本到初始聚类中心的距离，找出最小距离把样本归入最近的聚类中心，如图2(a)所示。修改中心点的值为本类所有样本的均值，再计算各个样本到k个中心的距离，重新归类、修改新的中心点，如图2(b)所示。直到新的距离中心等于上一次的中心点时结束。

(a) 将未归类的样本放入最近的聚类中心

(b) 将归类的样本重新归入最近的类

K-均值算法在执行过程中，采用欧氏距离计算数据样本之间的距离，使用误差平方和准则函数评价聚类性能。给定样本集D={x1,x2,…,xm}，K-均值算法针对聚类所得簇划分C={C1,C2,…,Ck}最小化平方误差为:

(4)

K-均值算法需要给定初始聚类中心，不同的初始聚类中心会有不同的结果，而且必须事先给定聚类数目，然而聚类个数k值往往是难以估计的。

3 粒子群算法

粒子群算法是一种群体智能的优化算法，它从鸟群觅食行为特征中得到启示[15-17]。假设粒子群由m个粒子组成，用种群X={X1,X2,…,Xm}来表示，当它在一个n维空间中，其中第i个粒子所处的位置用Xi={Xi1,Xi2,…,Xin}T表示，每个位置都表示一种解。粒子通过不断调整自己的位置Zi来搜索新解，第i个粒子搜索到的最好解，记做Pid，整个粒子群经历过的最好的位置，即目前搜索到的最优解，记做Pgd。此外每个粒子都有一个速度，记做Vi={Vi1,Vi2,…,Vin}T，当2个最优解都找到后，每个粒子根据式(5)～式(6)来更新自己的速度和位置[18]。

图3 粒子移动方向的示意图

速度向量迭代公式：

Vid(k+1)=ωVid(k)+c1r1(Pid(k)-Xid(k) )+

c2r2(Pgd(k)-Xid(k)) (5)

位置向量迭代公式：

Xid(k+1)=Xid(k)+Vid(k+1)

(6)

其中，Vid(k+1)表示第i个粒子在k+1次迭代中第d维上的速度；ω为惯性权重，通过调整ω的大小，可以对全局寻优能力和局部寻优能力进行调整；c1、c2为非负常数，r1、r2为0～1之间的随机数；Pid(k)表示第i个粒子在第d维空间中k次迭代中的个体最优值；Pgd(k)表示全局最优解。

4 优化的粒子群算法

在算法的初期阶段，粒子飞行的方向和位置全部取决于速度，保持粒子高效可靠的遗传性，必须提高粒子速度的发散概率，为此要将粒子收敛速度降低。在PSO算法中的公式可以观察到，存在ω、c1、c2等随机参数，惯性权重ω使粒子保持运动惯性，c1、c2表示粒子向Pid(k)和Pgd(k)位置的加速项权重[19-21]。常用的惯性权重公式如下：

ω(k)=ωmax-(ωmax-ωmin)×k/itermax

(7)

ω(k)=ωmax-(ωmax-ωmin) (k/itermax)2

(8)

其中，ωmax表示最大惯性权重；ωmin表示最小惯性权重；itermax表示最大迭代次数；k表示当前的迭代次数。

上述惯性权重都为线性权重，虽然符合整个搜寻过程中惯性权重递减的要求，但在算法搜索过程中，种群粒子在靠近某些边缘最优解时，可能存在种群多样性的缺失，寻优性能上还有提升空间。众多学者纷纷将固定惯性系数进行动态调整以此改善PSO算法过早收敛到局部最小值的弊端。例如，阮威[22]将动态惯性系数定义为分段函数，将所有粒子当前平均适应度和粒子i当前适应度的大小关系作为分段条件，得到2个线性的惯性系数；姜建国等[23]采用余弦函数的形式来控制惯性权值的变化；杨雨航[24]将动态惯性权重服从一个指数分布概率密度函数。结合上述对改进惯性权重的分析，本文加入余弦函数控制线性权重的同时[24]，加入正态分布函数，使惯性权重在整体上呈现非线性变化。优化的惯性权重公式如下：

(9)

其中，N(0,1)为正态分布，φ为惯性调整因子。余弦函数惯性权重的改进策略为非线性地减小ω的取值,使种群粒子更快地接近最优解，提高了搜索效率，相对于阮威提出的线性动态惯性权重，不仅在搜索效率上更高,还能够改善早熟问题。姜建国提出的余弦函数控制权值变化，在搜索后期，会出现收敛速度降低和种群多样性缺失的现象。本文通过加入正态分布再次调整惯性权重的分布情况，以此改善上述现象，加入非线性随机的权重可以在每次迭代中改变粒子速度，保证种群的多样性。并通过φ控制取值范围的偏离程度，在搜寻最优解过程中，惯性权重减小可以通过φ值进行调控，降低在局部极小值处丢失全局最优解的概率。相较于杨雨航[24]仅仅把动态惯性权重服从一个概率密度函数，本文提出的控制偏离程度的参数φ的概念，完美结合余弦函数，增强了全局寻优能力。

学习因子的取值对粒子的“认知”能力与“社会”能力具有很大的影响，学习因子做出的变化为:

(10)

(11)

其中，c1s、c2s分别表示学习因子c1和c2的初始值，c1e、c2e分别表示学习因子c1和c2的终值；t表示当前迭代次数；T表示最大迭代次数。

这样的改变使得粒子的“认知”能力和“社会”能力得到了充分的发挥。“认知”能力的加强便于实现快速搜索，提高全局搜索能力；“社会”能力的加强有利于局部的精细化，获得更好的全局最优解。确定好权重系数与学习因子之后，PSO算法就可以在搜索算法初期，仅使用PSO算法在全局寻优过程中不断逼近解子空间，增加收敛的速度。一旦PSO算法处于收敛状态，此时每个粒子的适应度相同，是切换K-均值算法的最佳时刻，充分发挥K-均值算法局部寻优能力，加快收敛速度。

粒子群适应度方差σ2定义如下：

(12)

图4为优化算法流程图，它包括2个阶段:

1)使用PSO算法在解空间中搜索全局最优解，利用PSO算法优异的全局优化能力，以避免收敛到局部最优解。当找到全局最优解或近似全局最优解时，停止PSO算法切换至K-均值算法。

2)利用K-均值算法进一步优化。在第1阶段寻找到的全局最优解可以看作是K-均值的聚类中心。

5 实验结果与分析

5.1 定性分析

为了验证本文改进算法的有效性，选取2个标准的基准测试函数对本文改进PSO算法和传统PSO算法进行测试。

Rosenbrock函数的非凸函数:

(13)

Schaffer函数：

(14)

算法参数设置如下：种群规模为30，粒子维数n=10,迭代次数T=50。2类函数优化结果如图5所示。

图4 PSO优化K-均值算法流程图

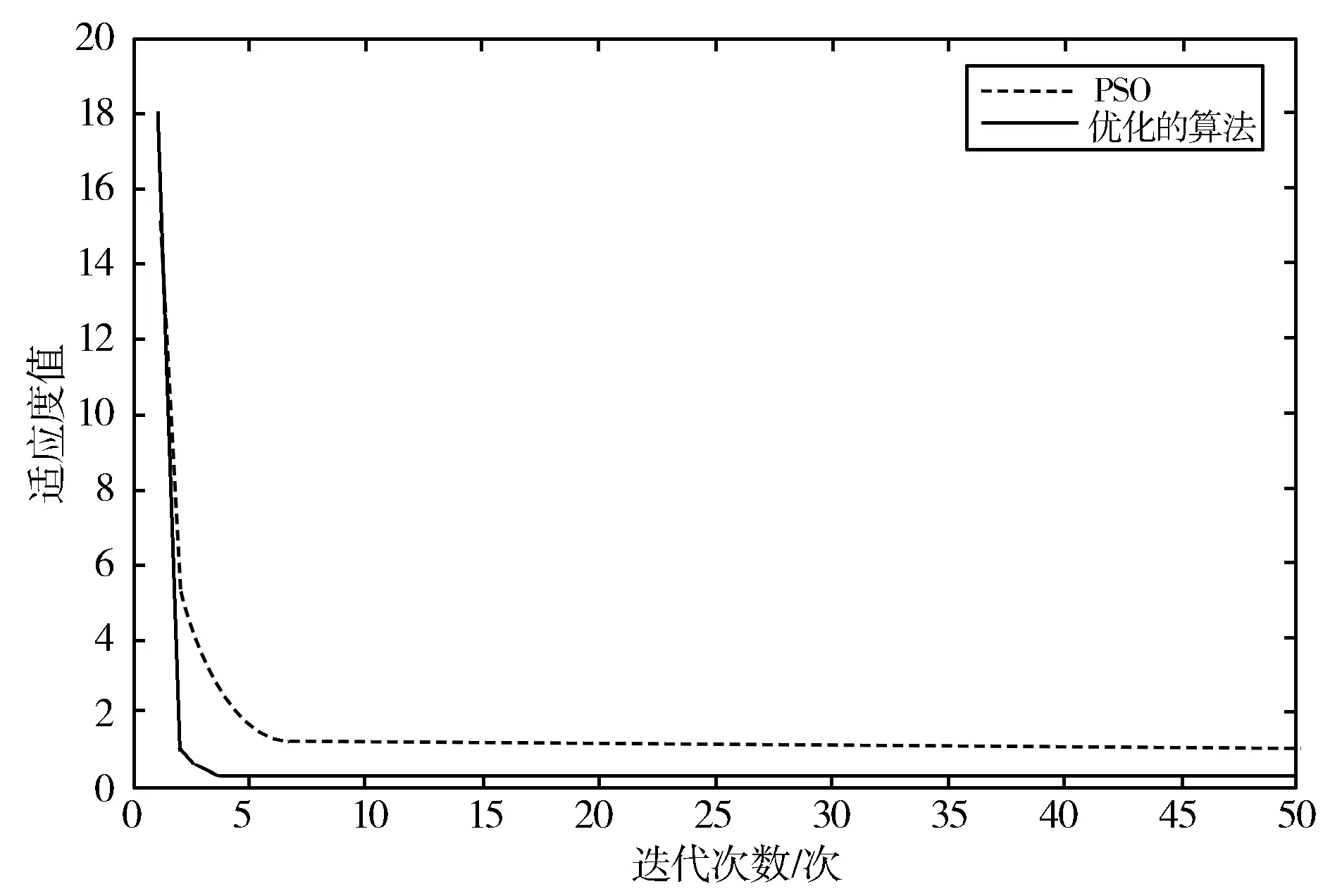
(a) Rosenbrock函数迭代过程图

(b) Schaffer函数迭代过程图

图5(a)和图5(b)给出了优化算法和PSO算法分别在测试函数中迭代50次的曲线图。

从图5(a)中可以看出，优化的算法虽在其收敛速度上和传统PSO算法相差甚少，在50次迭代中都能很快接近最优解，但在优化精度上相较于传统PSO算法有明显提高；图5(b)中，PSO算法在此测试函数中曲线有强烈的震荡性，很难搜寻到最优解，而优化算法不仅在优化精度上远比PSO算法精确，还在收敛速度上更胜于PSO算法。整体来说，本文提出的优化算法有更强的搜索最优解的能力。

5.2 定量分析

为验证算法的优势，在Matlab环境下对3幅图像分别采用K-均值算法、PSOK和本文改进算法进行分割试验。图片分割效果如图6所示。

(a) Lena原图 (b) K-均值算法 (c) PSOK算法 (d) 本文改进算法

(a′) Orangutan原图 (b′) K-均值算法 (c′) PSOK算法 (d′) 本文改进算法

(a″) Flower原图 (b″) K-均值算法 (c″) PSOK算法 (d″) 本文改进算法

图6第1行分别为Lena原图、K-均值算法实验结果、PSOK算法实验结果和本文改进算法实验结果，从图6中可以看出，图6(b)有轻微曝光现象，人脸细节分割不够细致，图6(c)在特征细节都有所凸显，但稍微有些色差，图6(d)在人物的帽顶、嘴唇、鼻尖、发梢以及肩部上的细节上更加清晰明显，较大程度上还原了Lena原图。第2行分别为Orangutan原图、K-均值算法实验结果、PSOK算法实验结果和本文改进算法实验结果，由图6可以看出，图6(d′)可以看出在猩猩的毛发、鼻子以及背景图的部分纹理最为清晰，整体轮廓清晰，色差较小。第3行分别为Flower原图、K-均值算法实验结果、PSOK算法实验结果和本文改进算法实验结果，图6(d″)的花瓣纹理、云彩背景干扰处理得更完善，还原度较高。综上所述，本文改进的算法提高了图像分割的质量。

在对3幅图像进行分割的同时，对不同算法的运行时间也进行了比较，比较结果如表1所示。

表1 不同算法运行时间 单位：ms

图像K-均值PSOK本文改进算法Lena242827902311Orangutan227426352023Flower169818751574

从表1中可以看出，K-均值算法、PSOK算法、本文改进算法的运行速度有明显不同，本文改进的算法分别在图像Lena、图像Orangutan、图像Flower的处理上用时最少。K-均值聚类算法具有简单、快速的特点。PSOK是一种融合算法，全局搜索能力强，但容易陷入局部最优，运行的时间较长。本文改进的算法通过结合PSOK算法和K-均值算法，并对权重系数和学习因子进行改进，能准确寻找从全局搜索到局部寻优的切换时机，提高了运行效率。

6 结束语

本文提出了一种基于粒子群优化算法和K-均值聚类的优化算法，通过不断调整并改进粒子群权重系数和学习因子的策略促进粒子快速收敛至全局最优，改善了粒子群算法存在的收敛性与多样性之间的矛盾。改进后的算法既保留了K-均值聚类算法收敛速度快的优点，又克服了粒子群算法易陷入局部最优的缺点。

实验结果表明，PSO算法与K-均值算法的结合具有更好的稳定性，改进的算法提高了图像分割的质量和效率。粒子群优化技术已经开始活跃在众多领域，在以后的研究中更是热门话题。