基于LSTM的工业互联网设备工作状态预测

李兆桐，张卫山，郭武武

(中国石油大学(华东)计算机与通信工程学院，山东 青岛 266580)

0 引 言

工业互联网技术在现代工业中起着至关重要的作用，实时监控设备运行状态，通过对数据进行分析提前干预设备，可降低设备故障率从而降低生产成本。为此，利用收集到的传感器数据建立设备工作状态预测模型，用于预测设备在接下来一段时间的运行状态显得格外重要。

然而，在实际的工业生产环境中，由于设备受到内外部环境影响，其产生的数据也具有时变性，使用历史数据所学得的模型无法准确预测当前设备的状态信息[1]。除此之外长时间序列的序列时很难被分类[2]。当设备数据高度离散且在多个时间段相互重叠时，简单的单信号预测和阈值方法将会失效[3]。

随着近几年深度学习的发展，基于深度学习建立预测模型得到了广泛的应用[4-6]。在基于深度学习的建模方法中重要的一步是特征提取，许多研究人员已经将其应用在传感器数据的处理中来提取关键特征[7-10]。基于上述问题，不能只考虑简单的几个数据特征来预测设备运行状态。

在实际工业环境中，设备原始数据有以下特性：

1)由于传感器和网络传输故障导致部分缺失值和异常值。

2)数据的维数随传感器数目的增多而增大且部分传感器数据之间存在冗余项。

3)故障数据少，数据倾斜情况严重。

针对设备运行状态的变化，所构建的模型需要随着时间的推移适应设备状态的变化。为此，本文提出一种基于LSTM的工业互联网设备工作状态预测方法。主要设计思路为：

1)进行数据清洗，去除异常值，填充空值。

2)采用PCA算法进行数据降维。

3)采用SMOTE算法进行数据倾斜处理。

4)基于LSTM神经网络构建预测模型。

1 相关研究

设备的故障诊断与预测一直是学者们关注的研究热点，近几年来，随着机器学习方法的流行，越来越多的研究人员尝试将机器学习的方法应用到设备状态诊断与预测中来。陈志平等人[11]采用基于奇异值分解优化的局部均值分解法提取电梯轿厢振动时频域特征，然后采用聚类分析进行电梯故障分析，采用回归分析实现电梯故障的预测。范李平等人[12]首先对变电设备故障影响因素进行相关性分析，选择影响因素，然后利用Logistic回归算法进行故障预测。王桂兰等人[13]使用XGBoost算法在风机主轴承故障预测中取得了良好的效果。Leahy等人[14]首先根据领域知识进行特征选择，然后通过随机网格搜索寻找超参数来训练支持向量机进行故障诊断。

然而，以上基于传统机器学习算法的研究仅适用于有限数据样本空间，在实际工业环境中，数据规模特别大，且数据之间具有高度的时间相关性，以上方法并不适用。

随着近几年深度学习[15]的快速发展，基于深度学习的时间序列分析也成为目前设备故障诊断与预测的一个研究热点[16-18]。国内的周剑飞等人[1]也提出了一种基于LSTM神经网络模型和滑动窗口技术进行设备故障的在线检测，但此方法并没有解决实际工业环境中数据严重倾斜的问题。

2 背景资料

2.1 PCA

在工业上直接通过设备传感器获得的数据往往具有非常高的维数且不同维数之间可能具有非常高的相关性，并且由于内外部环境的影响，传感器产生的数据一般都会具有噪声。基于以上原因，直接对传感器数据进行处理会产生算法的运行效率低、准确率不高等问题。在没有大量先验知识的情况下，对特征向量进行降维处理往往会取得较为理想的效果。

PCA(主成分分析)法是一种较常用的降维方法，其主要思想是利用坐标变换的思想，通过线性变换将数据从高维空间映射到低维空间中，同时保留数据的主要信息[19]。设原始数据样本包含m个n维特征向量Xk=(x1,x2,x3,…,xn)T,其具体计算步骤如下：

1)计算样本数据的平均值：

(1)

2)计算样本数据的协方差矩阵：

(2)

3)利用特征值分解方法求解协方差矩阵的特征值λ1,λ2,λ3,…,λi和特征向量ξ1,ξ2,ξ3,…,ξi。

4)将特征值从小到大排序，选取其中最大的k个，然后将其对应的k个特征向量组成特征向量矩阵P。

5)将原始样本数据投影到低维向量空间中：

Y=PTX

(3)

2.2 SMOTE算法

在实际问题中，异常数据往往只占正常数据的极小比例，而当前绝大多数机器学习算法都是基于正负样本比例相差不大的假设，因此严重倾斜的样本数据在某些情况下会导致算法准确性大大降低。例如：欺诈电话检测[20]、信息检索和过滤[21]以及机载直升机变速箱故障监测[22]等问题。

SMOTE全称是Synthetic Minority Oversampling Technique，即合成少数类过采样技术，它是基于随机过采样算法的一种改进方案[23]。其主要思想是利用少数类样本的近邻样本信息人工合成新样本。算法流程如下：

1)根据数据倾斜程度确定一个采样比率N。设少数类中样本数为T。对于少数类中的一个样本xold，计算该样本到其余少数类样本的距离(如欧氏距离)，得到其k个近邻样本。

2)从这k个近邻样本中任取一个xnear，然后按照式(4)生成新的少数类样本：

xnew=xold+rand(0,1)×(xnear-xold)

(4)

式(4)中，rand(0,1)生成一个0到1之间的随机数。

3)将步骤2重复N次，对于xold即可生成N个新样本。

4)对于少数类中所有样本执行上述操作，即可为该少数类合成N×T个新样本。

2.3 LSTM模型

LSTM(长短时记忆)模型通过在循环神经网络中添加遗忘门、输入门、输出门这3个门结构来实现信息的保护和控制[24]。

遗忘门，在构建神经网络的过程中将输入数据进行部分抛弃。该操作由一个sigmoid层进行选择，淘汰则输出为0，选择则输出为Wf·[ht-1,xt]+bf，具体方程如下：

Ft=σ(Wf·[ht-1,xt]+bf)

(5)

其中,ht-1表示上一个细胞的输出，xt表示当前细胞的输入，σ表示sigmoid函数。

输入门，更新细胞记忆部分，将部分记忆抛弃，部分记忆保存，并根据式(6)计算需要更新的信息：

it=σ(Wi·[ht-1,xt]+bi)

(6)

根据式(7)计算备选的用来更新的内容：

(7)

根据式(8)更新细胞状态：

(8)

输出门，首先通过式(9)来确定哪些细胞状态作为输出，然后将细胞状态经过tanh层进行处理获得(-1，1)之间的值,并和式(9)相乘获得输出ht：

Ot=σ(Wo·[ht-1,xt]+bo)

(9)

ht=Ot×tanh(Ct)

(10)

3 方法设计

本文提出的方法主要包括4个步骤：数据预处理、特征提取、模型构建、评估优化。处理流程如图1所示。

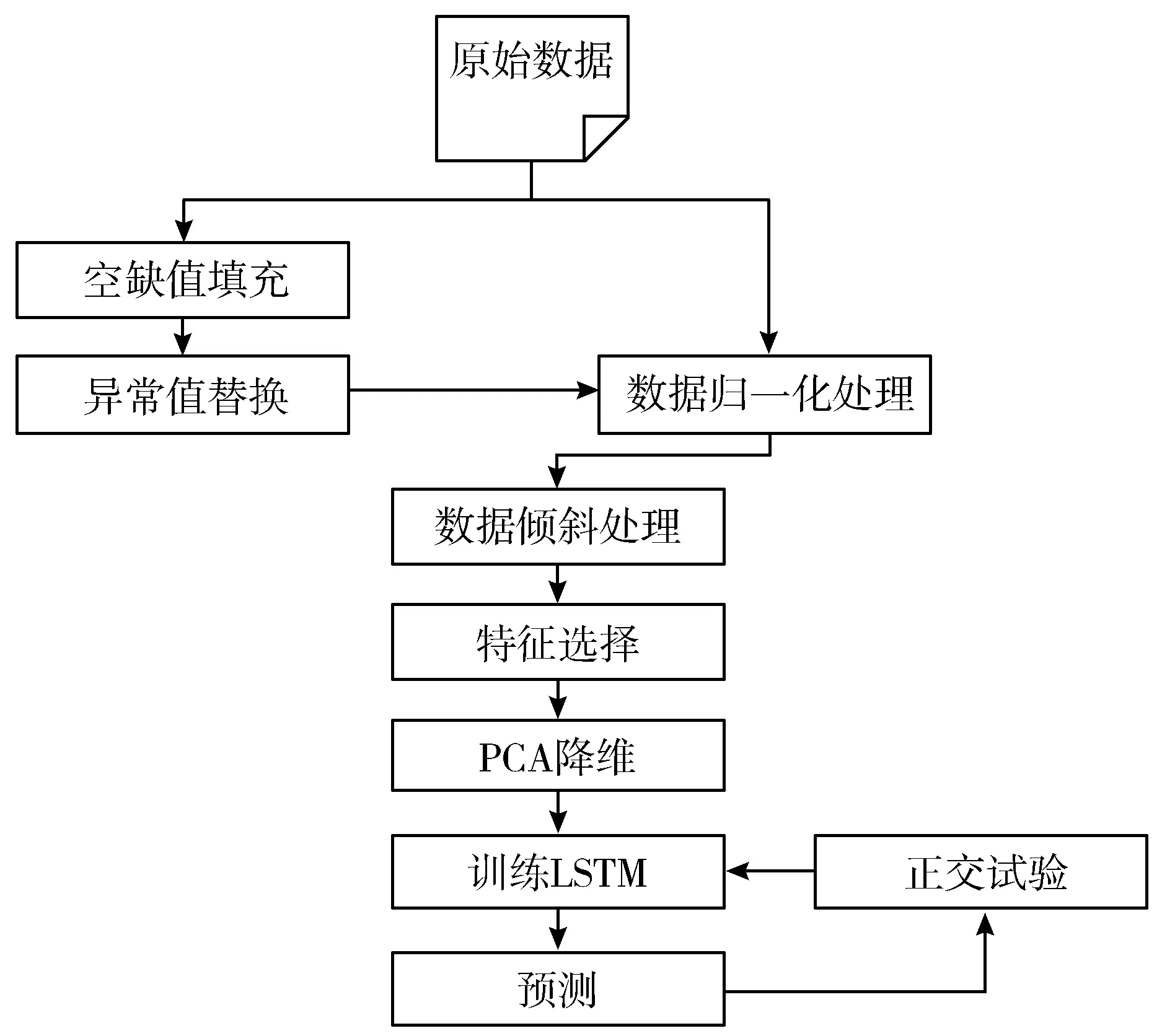
图1 处理流程

数据预处理：数据预处理主要解决空缺值的填充和异常值的排查和替换问题，其中还包括对数据进行归一化处理和数据倾斜处理。

特征提取：原始数据具有很高的维度，不利于模型的构建，利用PCA方法进行特征提取。

模型构建：利用TensorFlow深度学习框架来构建LSTM模型，通过OED(正交实验设计)来确定模型参数。

评估优化：评估采用F1分数。

4 实验与评价

4.1 实验数据

实验中的数据来自空调压缩机的真实传感器数据。每个空调压缩机中有44个传感器，每半分钟记录一次数据，其中包括温度、压力、功率等压缩机信息。将其中2/3的数据作为算法的训练数据，剩下的1/3作为算法的测试数据。

4.2 实验指标

本文通过训练深度学习模型将设备的工作状态问题转换为二分类问题：工作正常或工作异常。因此对工作状态的预测共有4种可能的结果：真正例(TP)、真负例(TN)、假正例(FP)、假负例(FN)。详情见表1。

由于本数据集中故障数据占比较少，采用普通评估方式即状态预测正确的百分比，可能评估效果较差，于是采用F1分数来评估算法效果。

表1 混淆矩阵

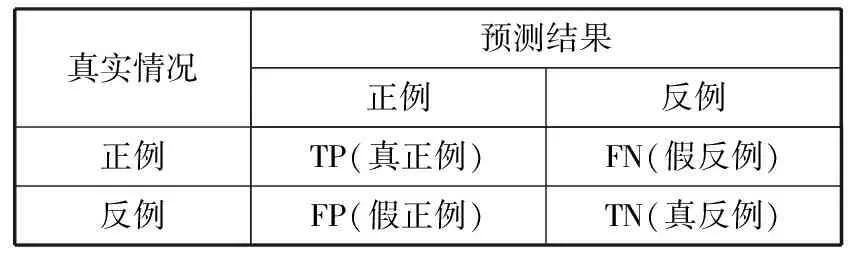
真实情况预测结果正例反例正例TP(真正例)FN(假反例)反例FP(假正例)TN(真反例)

P=TP/(TP+FP)

(11)

R=TP/(TP+FN)

(12)

F1=2×P×R/(P+R)

(13)

式中，P为查准率(Precision)，表示在所有被判断为正样本中真正正样本所占的比重；R为召回率(Recall)，表示在检测到的正样本占所有正样本的比重；F1是F1分数值，为两者的调和平均值。

4.3 实验设置

LSTM模型参数的确定，包括时间步、隐层神经元数量、批次处理大小和迭代次数。本实验采用3水平4因素的9组正交实验，设计表如表2所示。

表2 LSTM模型实验参数设计

实验号影响因素时间步隐层神经元数量批次处理大小迭代次数154102000258303000351250400041043040005108502000610121030007154503000815810400091512302000

根据模型参数需要，采用正交实验设计实验参数为时间步、隐层神经元数量、批次处理大小和迭代次数。其中每个参数设定为3水平。采用F1分数值来评估算法情况。

实验结果如表3所示。

表3 LSTM模型参数实验结果

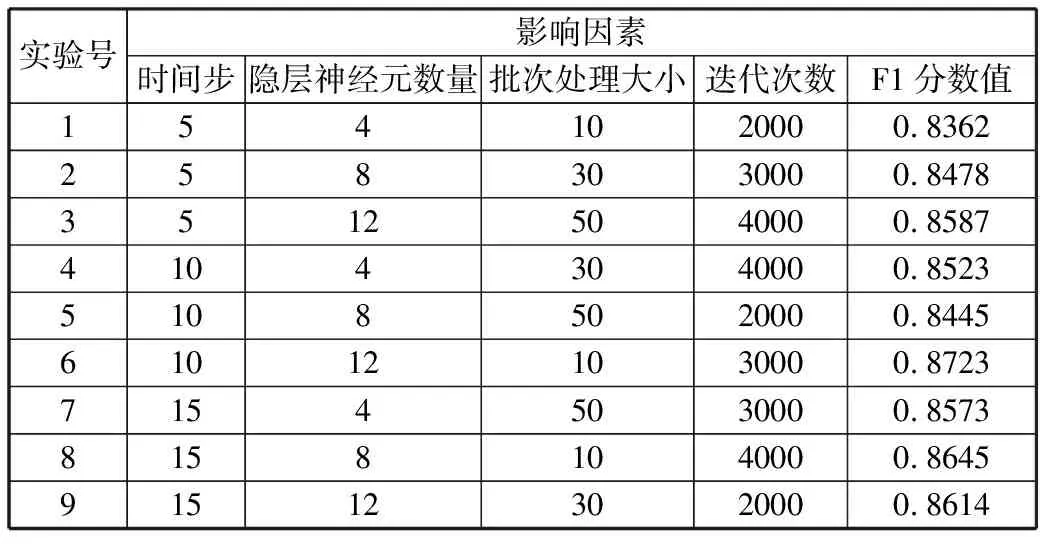
实验号影响因素时间步隐层神经元数量批次处理大小迭代次数F1分数值1541020000.83622583030000.847835125040000.858741043040000.852351085020000.8445610121030000.872371545030000.857381581040000.8645915123020000.8614

由表3可知，当时间步为10、隐层神经元数量为12、批次处理大小为10、迭代次数为3000时，F1分数值最大，即模型效果最好。

式(14)为相同水平的平均值，式(16)为计算表4中的Ri值，其中Ri越大表示该因素在该水平下对于算法的影响程度最大，例如表4中R2>R1>R4>R3，则R2对算法的影响程度最大。

(14)

Mean_Level=[Mean_Level1,Mean_Level2,Mean_level3]

(15)

Ri=max(Mean_level)-min(Mean_Level)

(16)

表4 因素影响程度

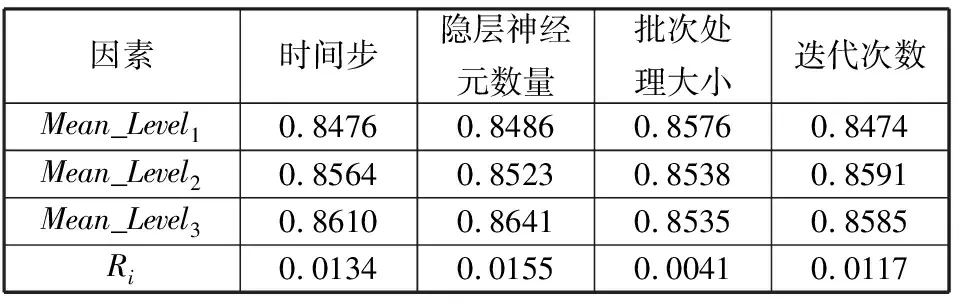
因素时间步隐层神经元数量批次处理大小迭代次数Mean_Level10.84760.84860.85760.8474Mean_Level20.85640.85230.85380.8591Mean_Level30.86100.86410.85350.8585Ri0.01340.01550.00410.0117

为进一步确定算法的预测效果，本文将提出的方法与Logistic回归、XGBoost进行实验对比，其中采用的数据为一整个月的空调压缩机数据。每组实验进行5次，取平均值。实验结果如图2～图6所示。

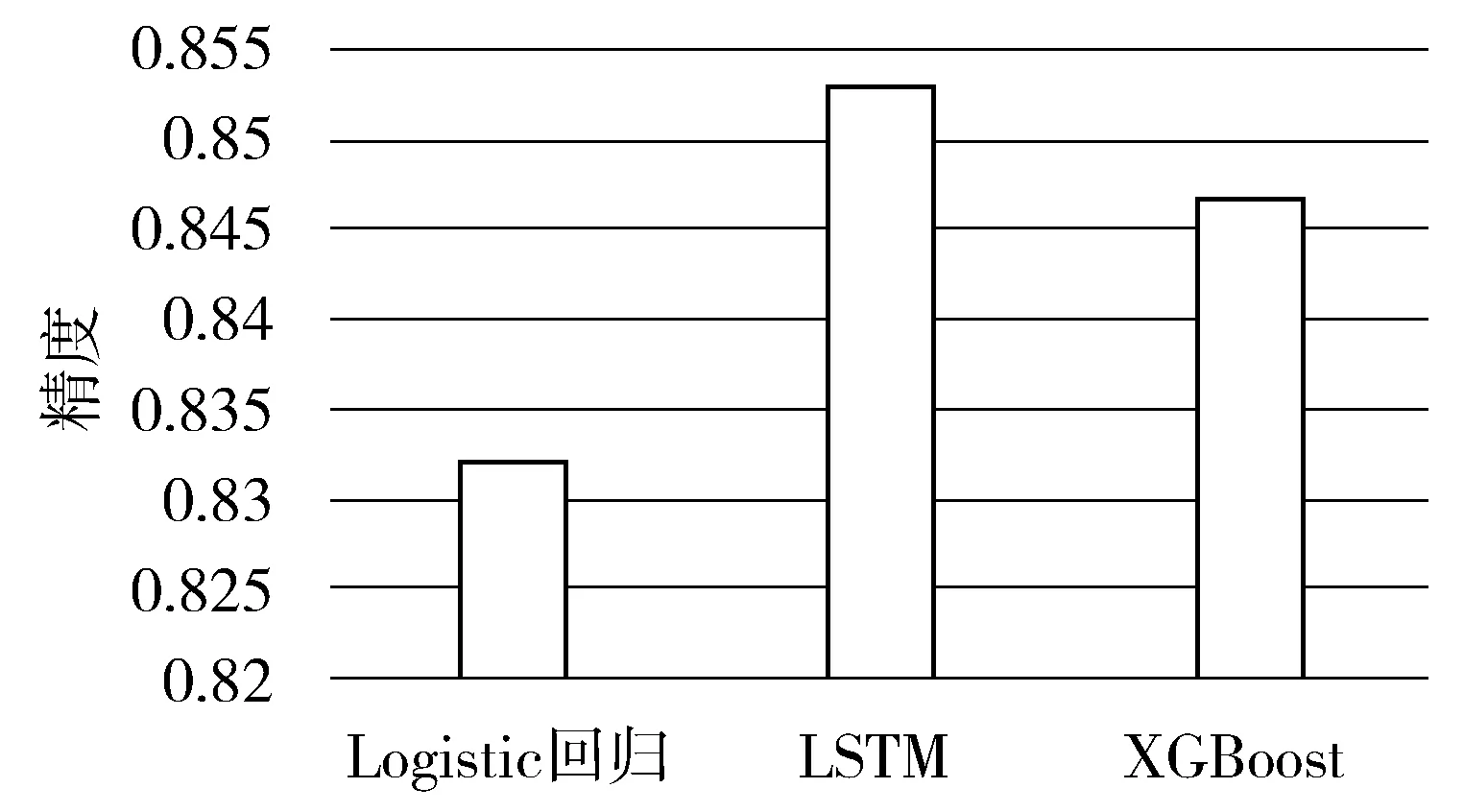
图2 不同算法的精度

图2所示的是不同算法的精度。Logistic回归的平均精度为0.8321，LSTM的平均精度为0.8531，XGBoost的平均精度为0.8467。

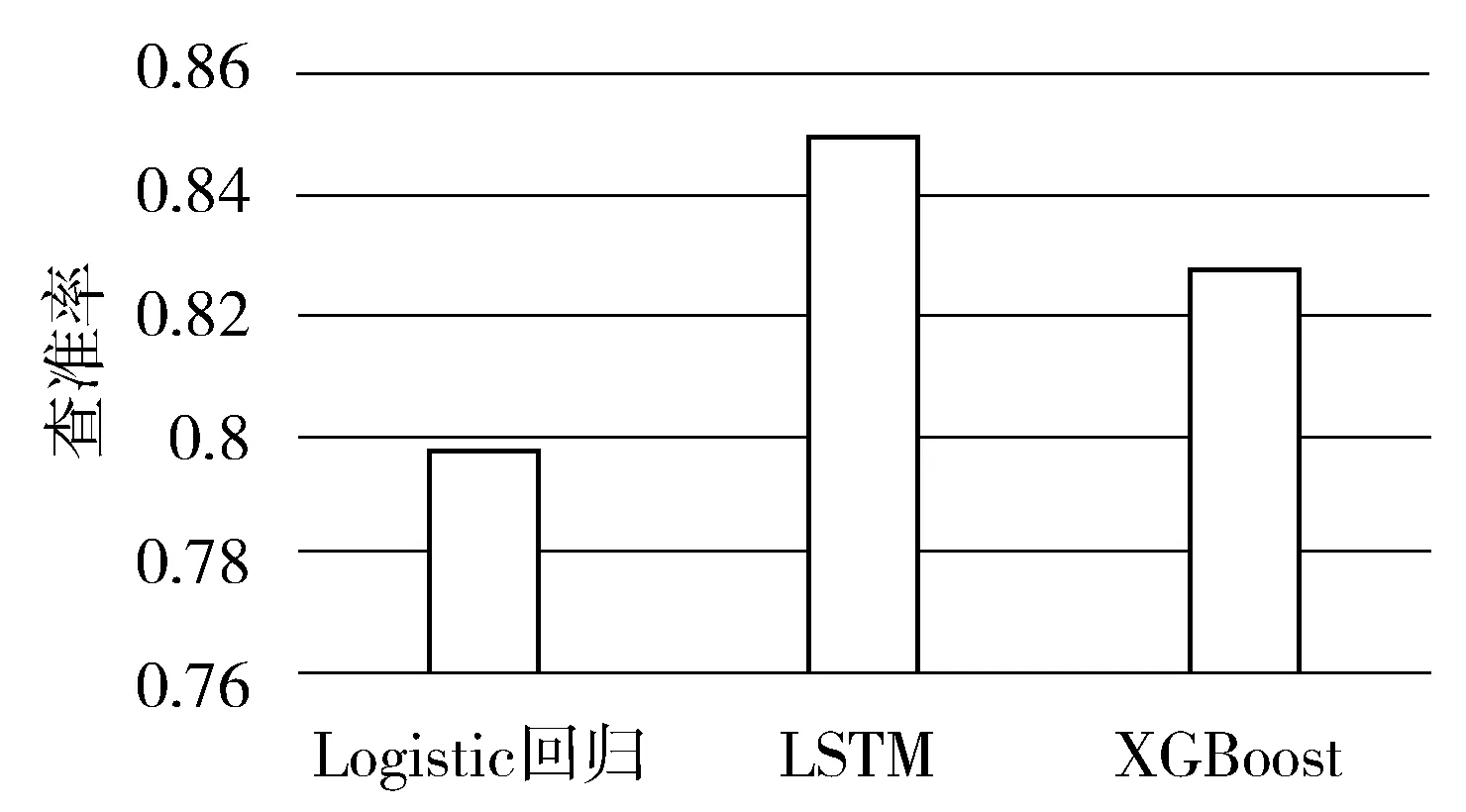
图3 不同算法的查准率

图3所示的是不同算法的查准率。Logistic回归的平均查准率为0.7976，LSTM的平均查准率为0.8492，XGBoost的平均查准率为0.8272。

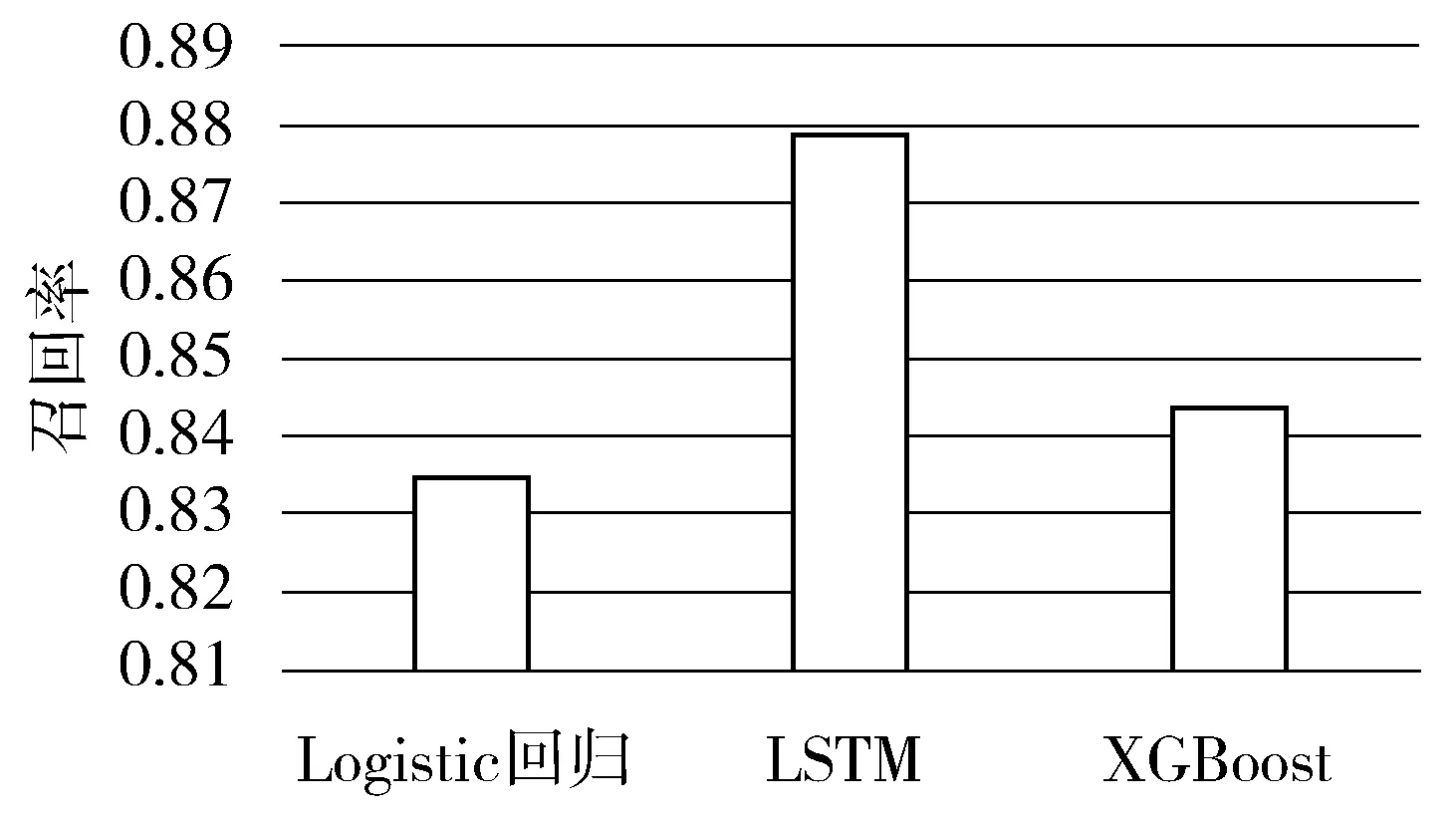
图4 不同算法的召回率

图4所示的是不同算法的召回率。Logistic回归的平均召回率为0.8354，LSTM的平均召回率为0.8789，XGBoost的平均召回率为0.8433。

图5所示的是不同算法的F1分数值。Logistic回归的平均F1分数值为0.8161，LSTM的平均F1分数值为0.8638，XGBoost的平均F1分数值为0.8352。

图2～图5的实验结果综合表明了在此空调压缩机数据集上本文方法的预测性能要优于Logistic回归和XGBoost算法。此外，比较各算法的训练效率，本文以训练时间代替训练效率，实验结果如图6所示。

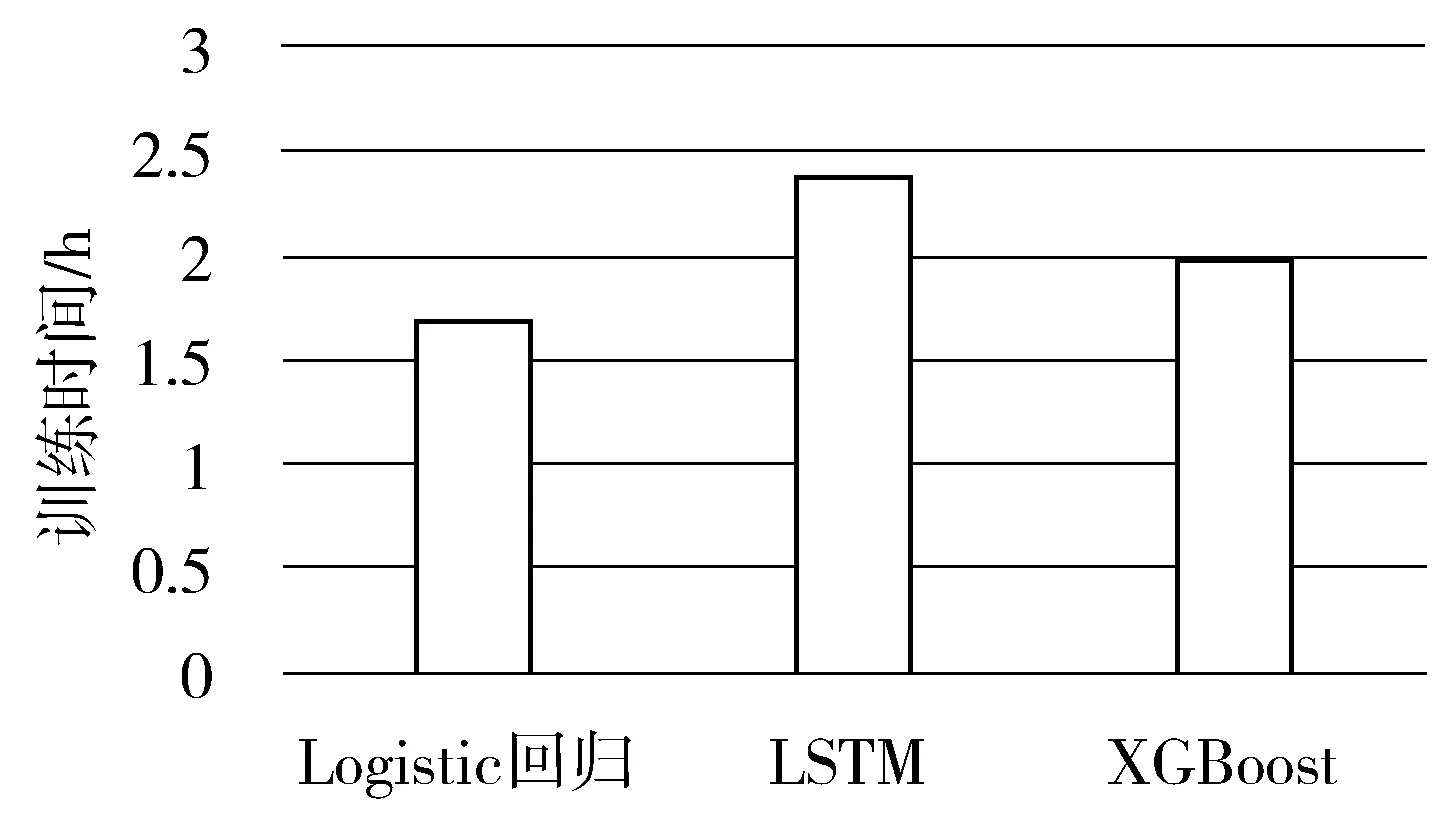
图6 不同算法的训练时间

图6所示的是相同数据量下不同算法的训练时间。Logistic回归的平均训练时间是1.7 h，LSTM的平均训练时间是2.4 h，XGBoost的平均训练时间是2 h。

图6的实验结果表明了本文提出的方法与Logistic回归和XGBoost在训练效率上还有待提升。

5 结束语

本文提出了一种基于LSTM的工业互联网设备工作状态预测方法，该方法包括了数据清洗和特征工程等在内的一整套数据分析流程。经过实验对比分析，在预测性能方面要优于XGBoost等算法，但算法的训练效率还有待提升，未来将从以下方面优化算法：1)使用其他特征提取算法来进一步压缩数据维度；2)SMOTE是过采样算法，考虑使用过采样与欠采样相结合的算法来处理数据倾斜问题。