一种不完全可测环境下的覆盖网络构造方法

廖 怡，盛益强，王劲林

(1.中国科学院声学研究所国家网络新媒体工程技术研究中心，北京 100190； 2.中国科学院大学,北京 100049)

0 引 言

随着计算机和网络技术的不断发展，互联网中的接入设备不断增多，尤其是移动设备的爆发式增长，极大地增加了网络的移动性和动态性。互联网规模的扩展，服务需求不断增长，对服务需求的处理提出了更高的要求，如何有效地管理大规模异构节点、提高服务质量是许多系统中的一个关键问题。在此背景下覆盖网络(overlay)构造技术应运而生。

覆盖网络是构建在现有的互联网基础之上，通过选择和连接节点构建一层新的网络，节点之间通过虚拟逻辑链路连接起来，提供类似基础设置所提供的基础性服务，如路由、组播、内容分发等[1]。覆盖网络通过探测底层物理网络的链路状态信息，并可根据需求在覆盖网络中为数据流计算路由路径，再将数据流的转发路径发送给底层物理网络，由底层物理网络按指定的路径传输。由于在选择覆盖节点构建覆盖网络时，未充分考虑节点位置信息，或是对物理拓扑信息搜集不全或不准确，易导致拓扑不匹配问题[2]。拓扑不匹配主要指2个在覆盖网络中相邻的节点映射到实际物理网络中却相距很远，造成逻辑链路与底层物理链路不一致的现象[3]。在依据覆盖网络计算路由路径时，仅依赖覆盖网络本身，未充分考虑互联网基础设施的影响，易导致较大的时延开销[1]。

近些年来，基于主动测量技术的覆盖网络构造技术变得热门，该类方法通过测量跳数、时延、带宽甚至节点操作的历史数据等信息构造覆盖网络[4-6]。跳数、网络延迟、带宽等指标能较好地反映底层物理网络状态。通过网络测量可了解实时网络状态数据以便对覆盖网络结构进行调整，适应网络的动态性。然而基于测量技术的覆盖网络构造方法其主要缺点是需要测量全局信息，或是在有限的时间内难以获取足够多的节点信息，导致部分节点间的网络状态信息缺失，本文称之为“不完全可测量”(Incomplete Measurable)问题。为此，首先定义不完全可测网络的概念，其定义如下：

定义1不完全可测网络

不完全可测网络是指受网络测量条件及方法所限或者网络状态及网络条件所限导致网络状态信息不完全可测量的网络。

网络拓扑图可用G={V,E,A,W}表示,其中，V为网络中节点集合；E为节点间边的集合，表示节点间的连接关系；A为网络连接状态属性集合，该属性可以是跳数、时延、带宽等；W为A中对应属性的属性值集合。若在网络图中的对象x在a∈A的属性值a(x)为0，或者为空，则称该网络为不完全可测网络(Incompletely Measurable Network， IMN)。

为解决信息不完全可测量的问题，在其他领域已有一些研究工作。文献[7]提出了利用状态估计的方法解决复杂网络中无法直接测量所有状态变量的问题，通过状态估计方法减少由于不完全测量引起的偏差。在无线传感器网络中，可依据网络测量技术对节点进行定位，也存在不完全测量问题。文献[8]针对不完全测距(即节点间的测距信息不完全，如传感器网络中因电子干扰、传感器探测范围有限和障碍物遮挡等因素导致部分节点间距离不可测)的高精度移动节点定位问题提出了基于分布式的多维标度定位算法进行局部定位与拼合，给出不完全测距下的移动传感器网络定位算法。

文献[2]提出了一种基于测量的启发式拓扑匹配优化算法(Measurement-based Heuristic Topology Matching Optimization Algorithm， MHTMOA)。该算法包括了节点加入、退出和失效算法，用于维护一个或者多个树形覆盖网络，可应用于广域网络的覆盖网络构建。该算法通过网络测量技术，获取底层物理网络中局部节点的跳数信息，利用跳数三角形的边长关系，有效地将相近节点逐渐地汇聚，并通过三角不等式违反(Triangle Inequality Violation， TIV)感知以及启发式规则选择邻居节点，每个节点最终可获得一个准确度较高的邻居节点集合，生成的树结构能较好地与底层物理网络匹配。TIV可对路由路径进行优化，可有效减少长路由路径，降低路由时延。

然而，MHTMOA拓扑构造方法也面临着“不完全可测量”问题。在MHTMOA中网络测量为按需测量，“需要什么测什么”。该方法易受网络实时状态的影响，一旦部分指标不可测或不可获取，将导致节点加入失败。此外，随着节点规模的增大，单个节点所需测量的节点信息呈线性增长，拓扑维护代价过高。对于结构化的覆盖网络，尤其是在节点频繁加入、频繁退出的高搅动系统中，需要一个复杂度低、易于实现和维护的节点加入机制以提高系统运行效率，节约运营成本。

为此，本文在MHTMOA的基础上实现一种用于不完全可测网络的低复杂度、易于大规模扩展的动态生成树方法TCIM(Topology Construction for Incompletely Measurable)，以解决MHTMOA所存在的生成树扩展性较差、难以适用于节点频繁加入/退出的环境、网络信息难以完全测量等问题。该方法与MHTMOA的区别在于：

1)在MHTMOA中，采用路由跳数作为节点加入指标，以选择临近的邻居节点；在TCIM中，对指标进行扩展，采用时延作为节点加入的指标，评估基于时延所得覆盖网络的性能。

2)在MHTMOA的基础上，提出一种基于常数测量次数的低复杂度节点加入算法，在保持一定的拓扑匹配准确度的基础上，根据节点规模和测量条件，自适应地选择常数个节点进行测量，以实现低复杂度节点加入。在后文中，称MHTMOA为高精度节点加入算法，高精度节点加入算法和低复杂度节点加入算法一起构成了TCIM。

1 相关工作

覆盖网络拓扑构造方法有着广泛的用途，在P2P[9-11]、无线自组织网络[12-14]、IP多播[15-17]等领域发挥着重要作用。随着网络虚拟化技术的发展，借助软件定义网络(Software Defined Network， SDN)，基于SDN的覆盖网络解决方案变得热门。SDN采用控制与转发分离架构，控制器作为集中式管理设备收集交换器相关的网络拓扑的信息和当前网络状态信息，用于制定数据转发路径。现有的许多SDN方案都是基于虚拟机所在的服务器上的软件交换器构建覆盖网络，SDN覆盖网络允许虚拟网络拓扑和配置独立于物理网络拓扑。

不同的覆盖网络设计可实现不同的目标。文献[18]提出了一种在SDN控制器通过基于位置感知的多播方法(Location-Aware Multicast Approach， LAMA)构建多组共享树结构，通过构建多个由交换器节点构成的共享树结构解决SDN覆盖网络的扩展性问题。在LAMA中，每个共享树可覆盖多个组播组，控制器首先对位置相近的多播源进行聚类。对于每个多播集群，控制器选择一个与所有组播源的最小距离的中心交换器作为其会合点(Rendezvous Point， RP)，然后构造从RP到其主机的最短路径组播树。基于构建的多组共享树，控制器可以在交换机上转发流的目数。文献[19]提出了一种基于覆盖网络的负载均衡方法，用于解决SDN中的流量工程问题。现有的覆盖网络有很多的优点，然而将经典流量工程算法应用于SDN覆盖网络中却存在问题。该方法利用SDN集中控制的优点，可针对异构流量实现负载均衡。文献[20]考虑采用基于OpenFlow的覆盖网络，建立现有网络中服务器到OpenFlow覆盖网络中节点的映射以降低系统迁移成本。提议方法根据VLAN标签、VM和物理服务器IP地址自动构建覆盖网络。

覆盖网络技术也被用作网络叠加层以增加网络弹性和恢复力。文献[21]提出了一种通过“路由拐点”集合形成覆盖网络的方法，并利用该覆盖网络选择2个数据中心之间最适合底层流量QoS需求的路径。文献[22]提出了一种弹性覆盖网络(Resilient Overlay Networks， RON)，在该网络中通过主动测量技术探测覆盖网络中节点间的链路状态，并基于测量结果构建覆盖网络。在该方法中，在构建弹性覆盖网络时需考虑底层网络的结构。主动测量能够帮助覆盖网络快速地对故障做出反应，以便及时对网络状态进行调整，提高网络的弹性。文献[23]提出了一种基于并行化蚁群算法的网络测量方法，解决网络测量节点的自动选取问题。该方法对传统蚁群算法进行改进，使其适用于网络测量中测量节点的选取。其次，该文中设计并实现了蚁群算法的并行化框架，所提出的并行化蚁群算法不仅能满足网络测量节点选取的要求，同时相比于非并行化算法具有更快的收敛速度，更适用于大规模网络测量。文献[24]提出了一种与网络操作无关的关键任务弹性覆盖网络(Resilient Overlay for Mission Critical Applications, ROMCA)。该方法使用中央目录服务器存储节点拓扑信息以简化节点发现过程，使用分布式的路由协议构建不同的覆盖网络之间的路由，并使用基于ICMP的traceroute定期测量实现多路径路由，实现覆盖网络之间路由路径的多样性。

此外覆盖网络也被应用于内容的传播和推送。文献[25]提出了一种用于地理分布式的数据中心中，发布/订阅系统的主题连接覆盖网络(Topic Connected Overlay， TCO)构建方法。该构建方法同样考虑将底层信息合并到覆盖网络设计中，对每个主题构建子覆盖网络树结构。TCO中的节点是所有对相同主题感兴趣的用户节点。为使构建覆盖拓扑有益于底层订阅/分布系统网络流量的最小化，在构建覆盖网络时捕获底层网络结构和节点间的物理位置，基于一些网络级度量指标来测量节点距离并作为TCO构建的权值。

综上，现有的覆盖网络可依据不同的需求和设计目标构建，为提高覆盖网络效率，可考虑利用底层物理网络信息构建拓扑，利用现有的网络测量技术获取节点间的位置关系以提高覆盖路由效率、QoS等，同时需考虑拓扑的维护代价、负载均衡、网络弹性、容错性和恢复力等因素。

2 一种用于不完全可测网络的拓扑构造方法

2.1 TCIM算法

TCIM由2个子算法构成，分别为高精度节点加入算法和低复杂度节点加入算法。其中高精度节点加入算法是基于MHTMOA[2]实现的，用于小规模或静态/低动态性条件下的节点加入；低复杂度节点加入方法是在MHTMOA生成的小规模树结构之后的节点加入，可用于大规模、高动态以及网络不完全可测条件下节点的加入。TCIM算法流程图如图1所示，其基本步骤是：

图1 TCIM算法流程图

步骤1检测网络中是否有节点加入/退出。若无，则系统等待，直到检测到节点加入；若检测到节点退出，则启用MHTMOA中的节点退出方法，完成节点退出，再等待新的节点加入/退出；若检测到节点加入，转至步骤2。

步骤2判断当前生成树的节点个数是否达到阈值N_initial。若当前生成树的规模未达到N_initial，先判断拓扑是否完全可测，转至步骤3。若当前生成树规模达到阈值N_initial，则启用低复杂度节点加入方法，完成节点加入。

N_initial的选择可根据用户自定义。使用高精度节点加入算法生成的覆盖网络可保持较高的拓扑匹配度；低复杂度节点加入算法的维护成本低，因而用户可根据所需生成的覆盖网络的精度需求和维护代价折衷地设置N_initial的值。

步骤3若所需的节点信息不完全可测，则切换到低复杂度节点加入方法，实现节点加入；若拓扑完全可测，则启用高精度节点加入算法完成节点加入。节点加入操作完成后系统等待新的节点加入/退出。

2.2 高精度节点加入算法

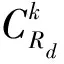
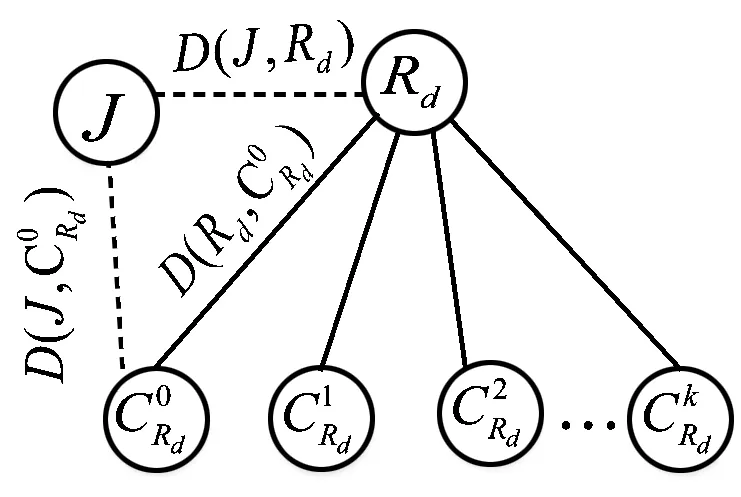
图2 时延三角形示意图

图3所示为按高精度节点加入算法生成的树形覆盖网络结构图。从图3(a)、图3(b)可看出采用时延指标的高精度节点算法生成的树形覆盖网络可较好地保持节点间的邻居关系，与物理网络匹配程度高。

图3 基于时延构建的生成树结构

2.3 低复杂度节点加入算法

若当前树形节点总数达到算法启动阈值N_initial，则启用低复杂度节点加入算法，算法流程如图4所示。其基本步骤如下：

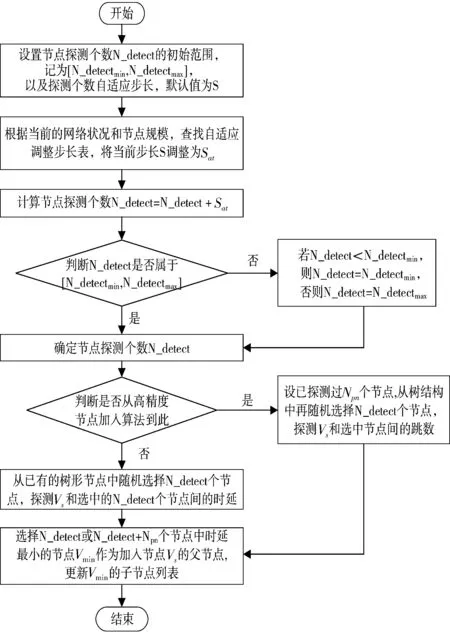
图4 低复杂度节点加入算法流程图

步骤1设置节点探测个数N_detect的初始化范围[N_detectmin，N_detectmax]以及自适应调整步长的默认值S。

步骤2利用网络感知技术，测量当前网络状态，获取网络状态参数，例如时延、带宽等，并以当前的网络状态参数和树形结构的总数作为节点探测自适应方法的输入参数，查找自适应调整步长表，得到当前节点探测个数调整步长Sat、当前节点探测个数N_detect=N_detect+Sat，其中Sat可正可负，最终得到动态的节点探测个数。

系统中先预存了一张网络状况指标-节点规模-调整步长的映射表。该表在对网络状况指标进行量化分级的基础上，结合节点规模，得到相应的调整步长Sat。

步骤3根据得到的N_detect，从已有的树形节点中随机或者有条件地选择N_detect个节点，利用网络测量技术测量待加入节点到探测节点间的时延。

步骤4选择时延最小的节点作为待加入节点的父节点；更新加入节点的父节点指针，更新选中的节点的子节点个数及子节点列表。

TCIM具有复杂度低、适用于大规模节点、适用于高动态性系统等优点。TCIM中的高精度节点加入方法相较于用最小生成树算法(例如Prime算法、Kruskal算法)，时间复杂度为O(ElogV)(其中E为边的总数，V为节点总数)。TCIM中的低复杂度节点加入算法将时间复杂度降为O(1)，时间复杂度低，有利于生成树的大规模扩展。其次，TCIM生成树方法是动态的，不需要获取网络全局信息，只需根据网络测量获得的少量局部信息即可完成节点的加入。在节点加入过程中，每个节点只需要存储邻居节点信息，可实现邻域自治，树形结构易于维护，算法的空间复杂度低。

3 仿真结果及分析

3.1 实验设置

本文的对比方法采用Anysee2中使用的经典的基于节点编码的最长前缀匹配算法[26]，并将该方法与界标法相结合作为对比算法(简称Landmark+Anysee)和Pan[27]在2015年提出的基于DHT的覆盖构造算法(后文简称Pan)，该算法利用不同的界标节点和IP来解决拓扑不匹配问题。在Landmark+Anysee方法中，界标个数为12。

本文通过BRITE拓扑生成器[28]产生了3种不同模型的网络拓扑，分别为Waxman、BA、Top-Down模型，作为底层物理网络，并在不同的网络节点规模下比较本文提议的TCIM算法与对比方法的性能。在3种网络模型中，BA模型和Waxman模型是扁平网络模型；Top-Down是自上而下的双层网络模型，tier-0表示AS级网络，tier-1表示底层网络节点。3种网络模型的度分布如图5所示，拓扑的参数设置如表1所示。仿真实验是在Window64、Intel i5 8250U CPU、8 GB RAM硬件环境中实现的。

图5 3种网络模型的度分布

表1 实验参数设置

参数名称设置节点规模N100,200,400,800,1600,3200,6400节点最小度m2节点带宽范围(100 kB,1 MB)Waxman参数α=0.15,β=0.2

本文使用Latency Stretch(LS)表示物理网络和覆盖网络之间的匹配度。此外还采用了文献[2]中定义的全局拓扑匹配比(GTMR)和局部邻居节点准确率(LNA)2个指标，从网络拓扑结构上描述覆盖网络与物理网络的匹配程度。GTMR表示在实际的物理网络中直接相连的2个点，根据节点加入算法加入树形拓扑结构后2个节点仍然保持连接关系的链路数占整个树形逻辑链路总数的百分比。LNA表示覆盖网络中单个节点1-hop邻居节点与其在物理网络中1-hop邻居节点之间匹配的比例。用节点加入过程中产生的消息数目作为拓扑维护代价。

对TICM算法仿真时，设置了2个参数N_initial和N_detect，分别表示低复杂度算法启动阈值和低复杂度算法中界标节点个数。在树结构生成时，首先指定物理网络中的一个节点为根节点，再随机抽取物理网络中其他节点按高精度节点加入方法添加到树结构覆盖网络中，直到节点规模达到N_initial；之后再按低复杂度节点加入方法加入覆盖网络，直到所有节点都完成加入，最后统计树形覆盖网络的GTMR、LNA和时延伸缩比、树的深度以及节点维护开销。对每个拓扑图重复试验了5次，选择不同的根节点和不同的节点加入顺序，统计仿真结果。

3.2 实验结果分析

1)时延伸缩比(Latency Stretch， LS)。

图6所示为3种网络拓扑模型下TCIM与对比方法的时延伸缩比的比较。LS表示覆盖网络中节点间路由路径的平均时延与底层物理路由路径的平均时延的比值，其理想值为1。时延伸缩比越低，表示覆盖网络结构与底层物理网络结构越匹配，路由效率越高。从图6可看出，在不同的节点规模和不同的网络模型中，TCIM的LS均小于对比方法。尤其是Top-Down模型中，TCIM的性能不仅优于对比方法，也优于Waxman模型和BA模型。在Top-Down模型中，处于同一个AS内的节点具有较低的时延，处于不同AS间的节点具有较大的时延，在时延上的显著差异有利于节点位置的区分，有利于相近节点的汇聚，因而时延伸缩比减少。

LS可以较好地反映覆盖网络与底层物理网络的匹配程度。笔者在文献[2]中，对高精度节点加入算法进行了研究。本文的仿真结果表明，高精度节点加入算法对时延指标仍然适用，利用时延作为节点间距离关系的度量指标所构造的树结构覆盖网络，依然可以较好地与底层物理网络匹配。

2)拓扑匹配准确度。

本文评估了BA模型下不同的N_initial和N_detect对拓扑匹配准确度的影响，统计不同的N_initial和N_detect参数下GTMR和LNA值的变化。分别统计了高精度和低复杂度节点加入方法混合以及全部使用高精度节点加入方法时生成树的GTMR和LNA值，统计结果如图7所示。

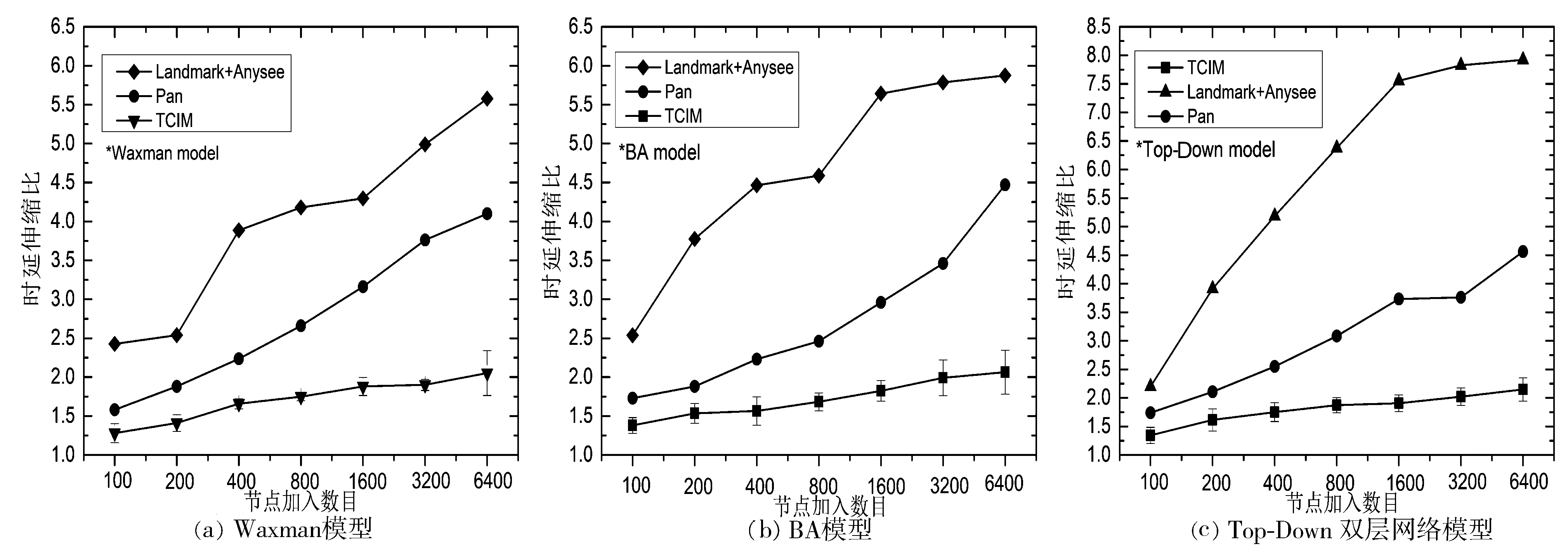
图6 3种拓扑模型下的时延伸缩比的比较

图7 BA模型下的高精度和低复杂度算法拓扑匹配准确度比较

在图7(a)中，当N_detect=0时，表示只采用高精度节点加入方法。从图7(a)可看出，在不同的N_initial条件下，使用低复杂度方法均使拓扑匹配准确度下降。当N_detect从4增至32时，GTMR和LNA的值几乎无明显变化。因而折衷考虑拓扑匹配准确度和节点加入代价，推荐N_detect的设置为4。从图7(b)可以看出，GTMR和LNA都随着N_initial的增大而增大，意味着使用高精度节点加入方法加入的节点越多，生成的树结构与底层物理网络匹配程度越高。

综上，可通过折衷考虑拓扑维护代价和拓扑结构匹配的准确度需求，合理设置N_initial值和N_detect值构建树形覆盖网络满足应用需求。

3)生成树深度。

图8所示为采用时延作为度量指标生成的树的深度与物理网络(图中用Graph表示)直径(最大跳数)以及Landmark+Anysee生成的树结构深度的比较。树结构的深度对覆盖网络中节点间的路由时延有影响。从图8可看出，TCIM生成树深度与物理网络直径呈正相关趋势，尤其是Top-Down模型中，正相关趋势表现显著。这也从侧面反映出TCIM生成树的拓扑匹配特性。基于最长前缀匹配方法的Anysee，其树深度受节点编码长度的影响，当树深度增加到编码长度时不再变化。

图8 3种拓扑模型下生成树深度比较

4)归一化拓扑维护代价。

图9所示为不同网络规模和不同的拓扑模型下，TCIM和对比方法的归一化拓扑维护代价。从图9中可看出，TCIM在Waxman模型和Top-Down模型中节点加入代价小于Pan方法。

图9 3种拓扑模型下的归一化拓扑维护代价比较

在Landmark+Anysee方法中，界标节点个数为常数，因而其维护代价不受节点规模的影响。TCIM随着节点规模的增大，树结构深度增加，导致所需测量的邻居节点个数增加，因而产生的消息数目增大,导致维护代价增大。Pan方法基于DHT算法实现，节点加入时存在多跳且需与邻居节点作比较，因而维护代价也随节点规模增大而增大。

本文进一步统计了不同节点规模下，使用高精度节点加入方法时动态根节点的切换次数，即循环迭代次数，结果如图10所示。从图10可看出，动态根节点的变化次数随着节点规模的增大而增大；且在BA模型下动态根节点的次数最少，节点规模100～6400范围内，迭代次数平均为2.75～4.25次。

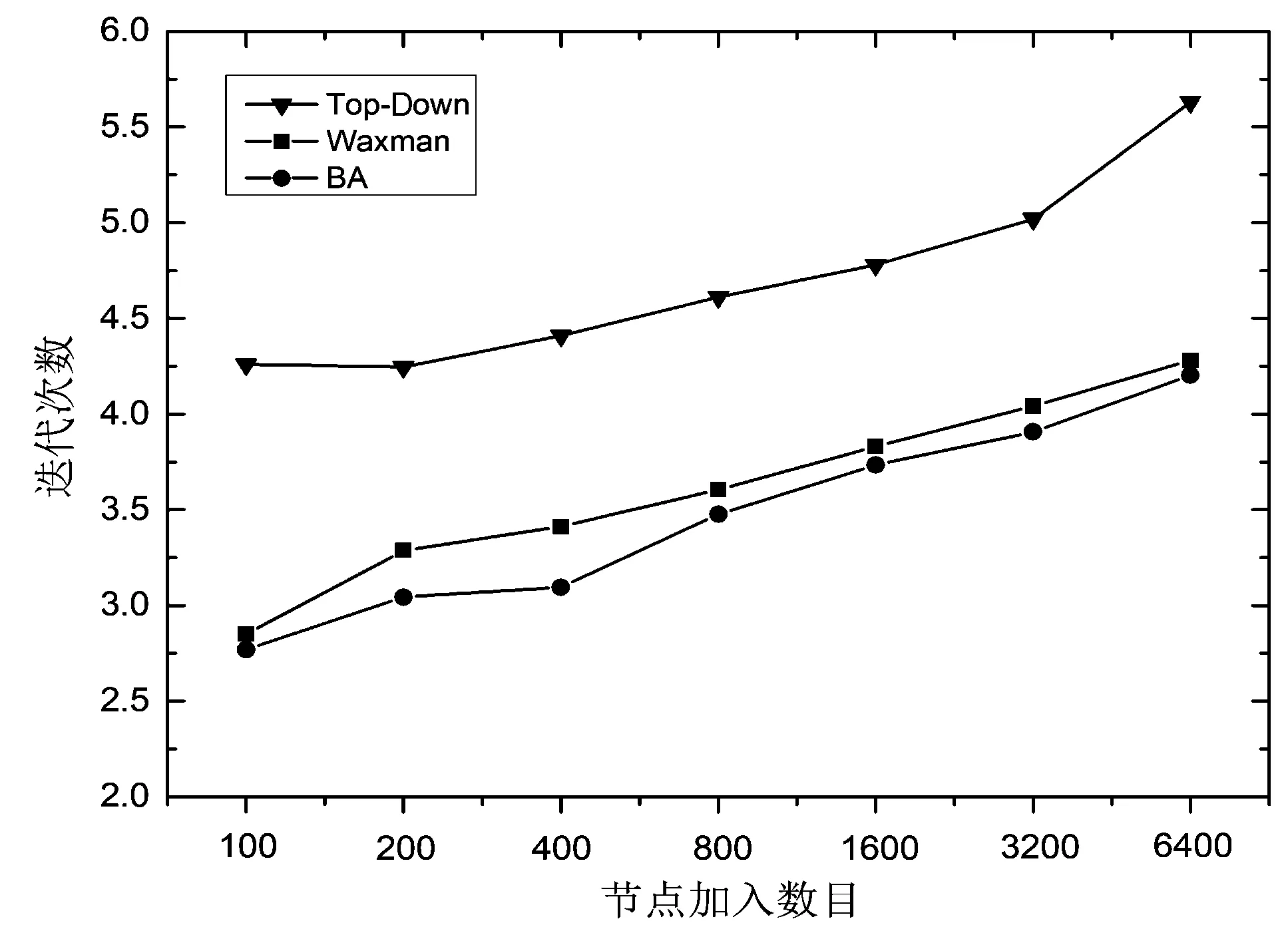
图10 3种拓扑模型下TCIM的循环迭代次数

4 讨 论

对于不完全可测网络，根据其信息缺失程度或信息可测量程度也有所区别。对于一个网络，只要存在某2个节点之间的网络状态属性值不可测量或无法获取，该网络即属于不完全可测的范畴。根据不完全可测网络中状态属性可测量的比例，不完全可测网络也可不同。通常获取全局信息较困难且测量代价过高，因而现有的若干基于网络测量的覆盖网络构造方法[2,4,6,24]多采用局部测量的方法，尽可能以最小的测量代价完成节点加入。虽然所得到的网络状态信息也是不完全的，但局部测量方法更倾向于状态信息虽然可测，但不全测。

5 结束语

本文针对基于测量的覆盖网络构建方法中的不完全可测问题，提出了一种用于不完全可测网络的树形覆盖网络构造方法TCIM。TCIM由高精度节点加入算法和低复杂度节点加入算法组成。高精度节点加入方法根据节点间时延测量结果构建时延三角形，再根据三角形的边长关系分为3种情况处理，最终把节点加入到覆盖网络合适的位置。低复杂度节点加入方法根据节点规模和网络状态自适应地选择常数个节点进行测量。其中高精度节点加入算法用于小规模或静态/低动态性条件下的节点加入；低复杂度节点加入方法可用于大规模、高动态以及网络不完全可测条件下节点的加入。

仿真结果表明，TCIM生成的树结构在不同的网络拓扑模型下均可取得较小的时延伸缩比(LS)，在Waxman模型和BA模型下有较小的拓扑维护代价。本文对比了不同的低复杂度算法节点规模启动阈值N_initial和低复杂度算法探测个数N_detect对生成树拓扑结构的影响，得到结论是：N_initial越高生成树的拓扑匹配程度越高；N_detect的推荐设置为4，当N_detect大于4时，即便增加测量个数对拓扑结构的准确度影响较小。为满足不同应用对构建覆盖网络的不同需求，应合理地设置TCIM中N_initial值和N_detect值构建树形覆盖网络，折衷地考虑拓扑维护代价和拓扑结构匹配的准确度需求。