基于神经网络逆控制的水轮机调节系统
陈艳琳,李志华,谢雪涵
(河海大学能源与电气学院,江苏 南京 211100)
0 引 言
频率偏差是衡量电能质量优劣的主要指标之一,频率偏差过大会导致整个发电系统运行不平稳,甚至会影响电网的稳定运行。水轮机调速系统主要致力于将水轮发电机组频率与电网给定频率进行对比,通过其差值来控制水轮机导叶开度,从而调节其本身转速,使机组的频率稳定在规定范围内[1]。然而水轮发电机组是一个复杂的、时变的非线性系统,使得传统的PID控制难以到达理想的控制效果。本文采用的神经网络逆控制是以逆控制理论为基础,结合神经网络能够逼近非线性函数的特点,将其运用到水轮发电机组系统中,建立逆控制器,再与被控系统构成伪线性系统,即实现对此系统的自适应逆控制,并通过仿真对所设计的控制系统进行仿真验证。
自适应逆控制[2-5]由美国斯坦福大学Widrow教授在1986年首次提出,它的提出在研究控制系统和调节器的学术界引起了不小的轰动。它的主要思想是利用被控对象传递函数的逆作为串联控制器来对系统的动态特性进行控制。目前,自适应逆控制思想已被应用到许多领域,如机器人控制[6]、感应电机调速[7]、噪声干扰消除[8]、发动机控制[9]、预测控制[10-11]、电机驱动[12]等。
1 水轮发电机组的自适应逆控制
1.1 带有非线性环节的电液随动系统
我国电力系统频率方面规定[13]在标称频率规定为50 Hz时,其允许的偏差绝对值不大于0.2 Hz。当水轮发电机组处于小波动工况下时,其整个系统的非线性程度不明显,可用近似的线性数学模型表示,如图1所示,此时传统的PID控制规律即可满足控制要求。
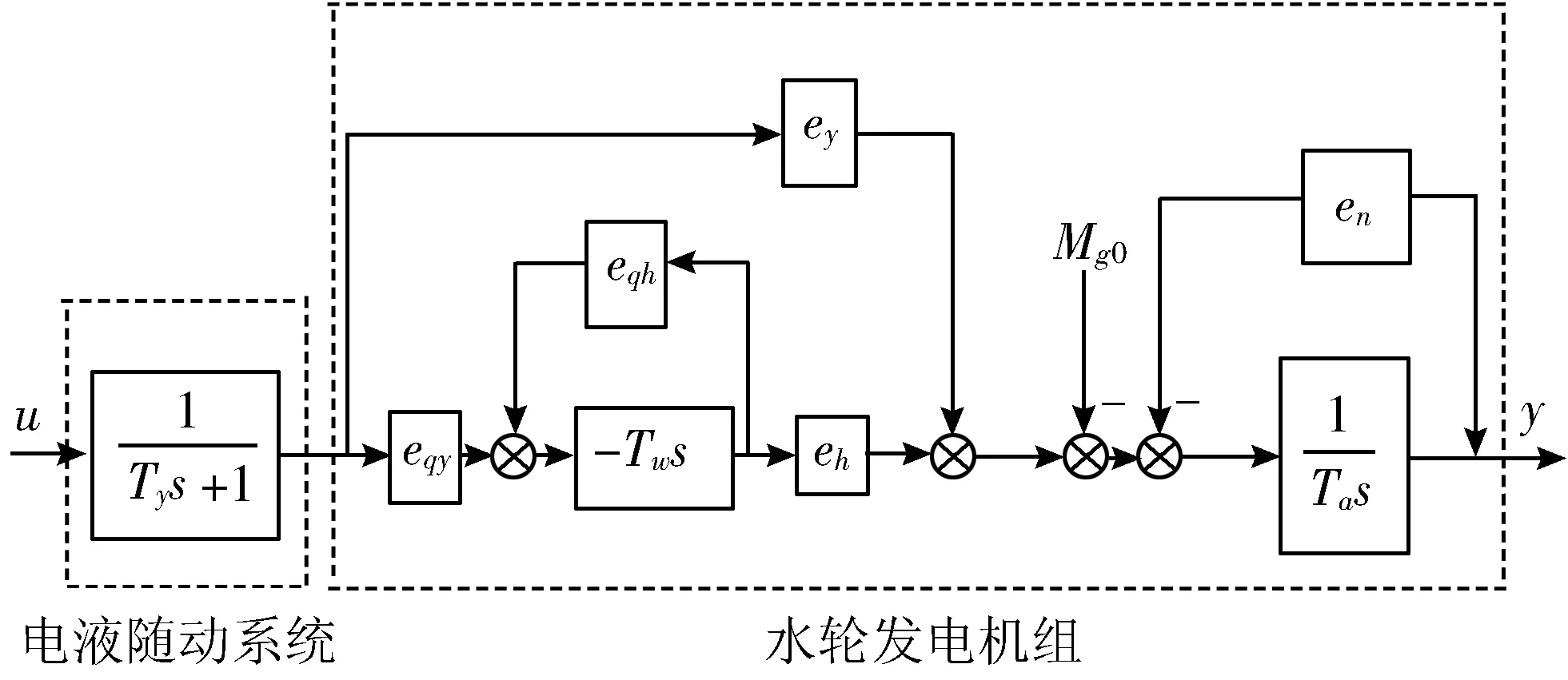
图1 系统简化数学模型
然而电网系统发生故障时,水轮机部件的非线性特征将突显出来,尤其是其中电液随动系统,即此时图1中的电液随动系统不再呈现简单一阶环节特性,随动系统中综合放大器与电液转换器之间、辅助接力器与主接力器之间会带有饱和非线性元件,主接力器输入端会带有死区非线性元件,如图2所示。
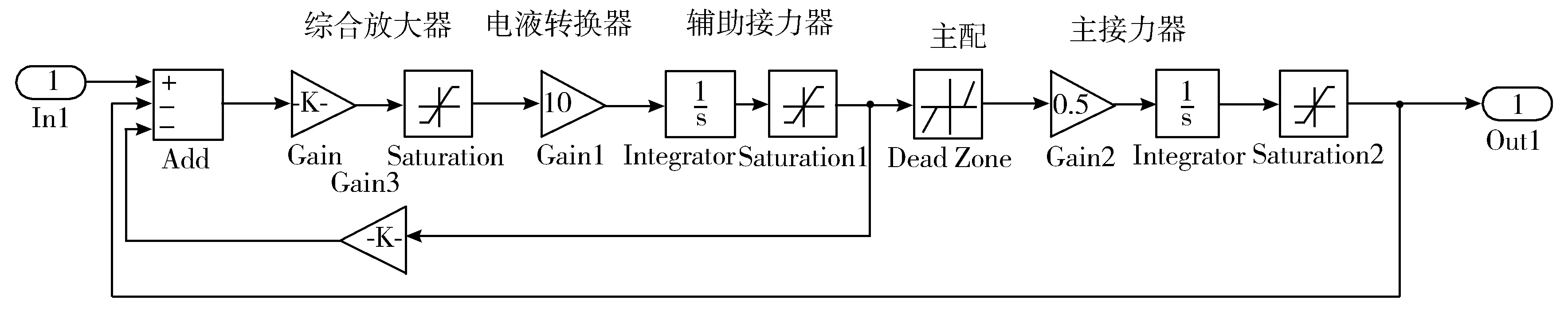
图2 带有非线性环节的电液随动系统框图
在接收到较大波动时,带有非线性环节的电液随动系统的接力器输出明显与只带有非线性环节的系统接力器输出有较大不同,为比较线性和非线性环节的随动系统模型对系统的影响,保持相关参数一致,让2种模型在高度为0、1的矩形脉冲下观察它们各自的输出响应,结果如图3所示。
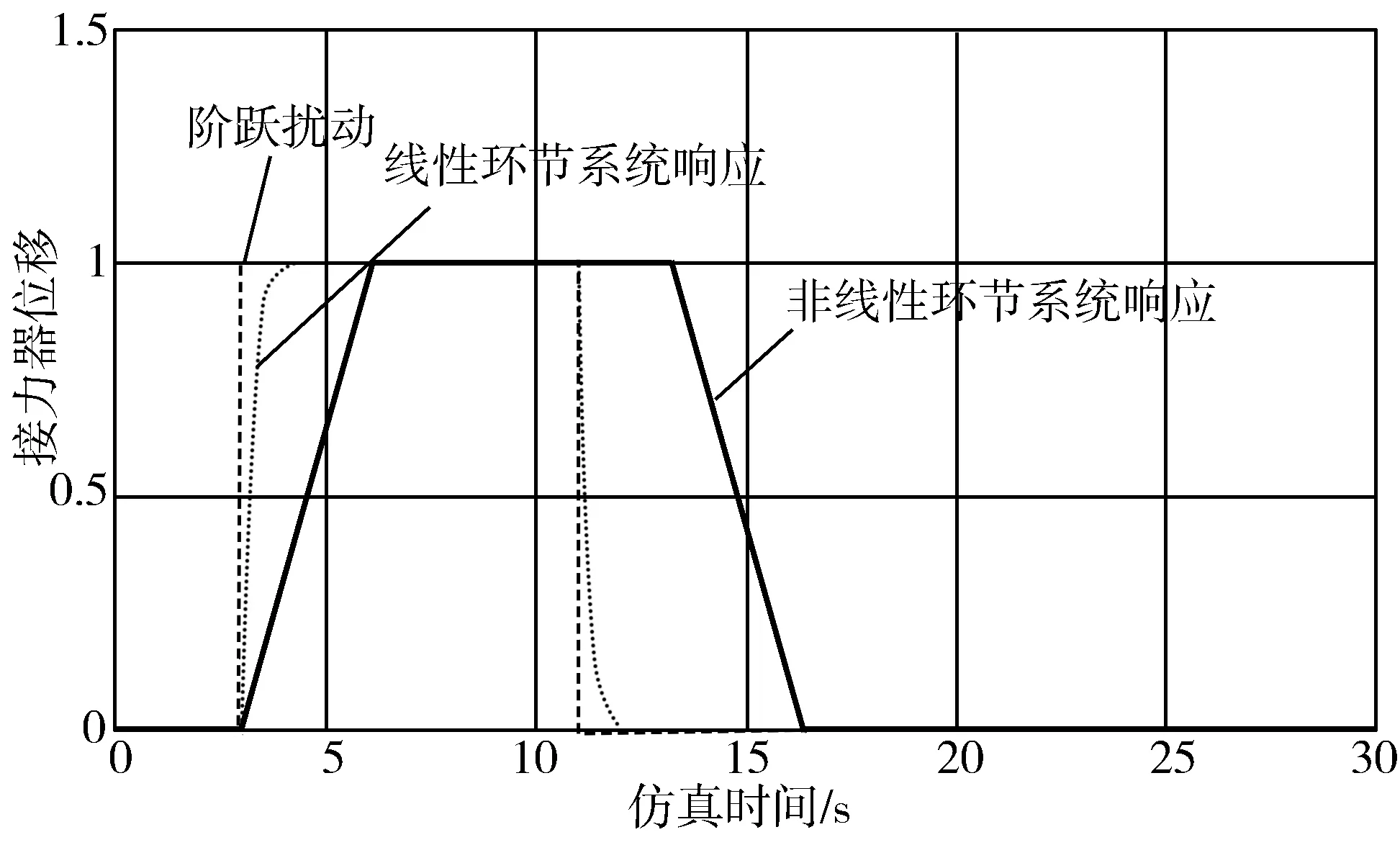
图3 电液随动系统仿真
从图3可以看出,当调节范围较大时,必须考虑系统的非线性环节,这种非线性因素主要由元件本身的物理结构引起,难以精确表示,此时传统的PID调节将不能满足系统控制要求。本文提出利用BP神经网络辨识被控系统的逆模型作为逆控制器实现自适应逆控制,具体的系统控制框图如图4所示。
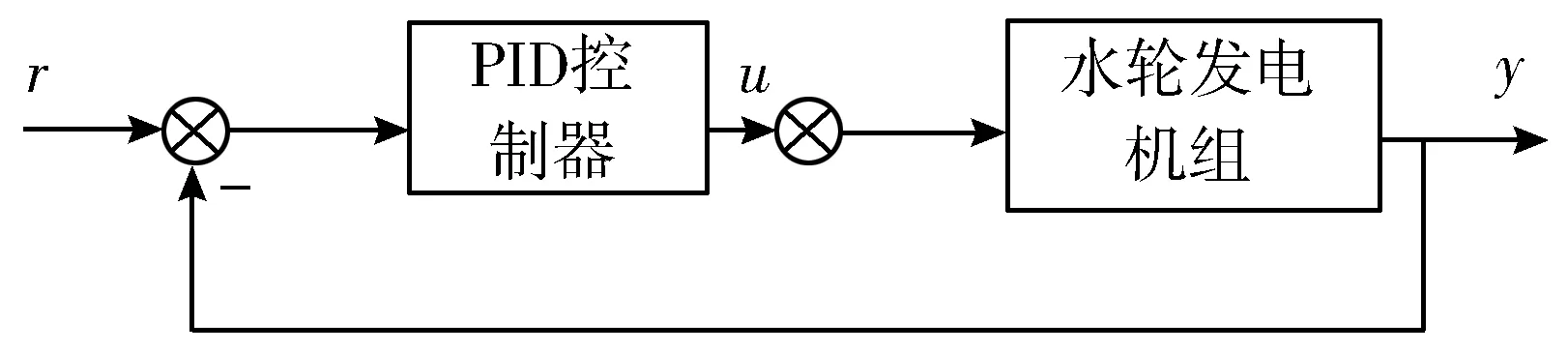
(a) PID控制
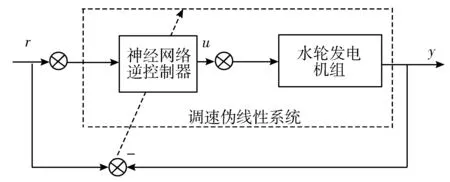
(b) 神经网络逆控制
1.2 水轮发电机组逆模型的在线辨识
水轮发电机组是具有死区、饱和等特性的非线性对象[14-16],其差分方程可表示为:
y(k+1)=g[u(k),u(k-1),…,u(k-m+1),y(k),y(k-1),…,y(k-n+1)]
(1)
式中,u和y分别为水轮机调速系统的控制输入信号和输出转速;m和n分别为输入、输出对应阶次。
为实现对水轮发电机组系统逆模型的在线辨识,采用BP神经网络作为辨识工具[17-21],其常用的多输入单输出结构如图5所示,关于BP神经网络具体的介绍可参考文献[22-24]。
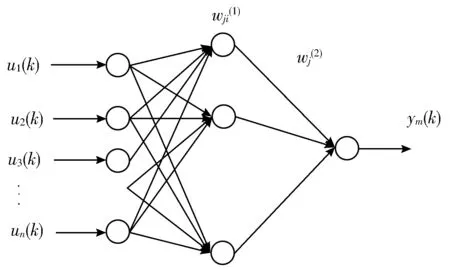
图5 BP神经网络结构
水轮发电机组系统作为对象在满足可逆的条件下,其对应逆模型的差分方程可表示为:
u(k)=g-1[u(k-1),…,u(k-m),y(k+1),y(k),…,y(k-n)]
(2)
根据自适应逆控制器以及BP网络本身学习算法的任务要求,此时BP网络的输入为:
(3)

(4)
(5)
(6)
(7)
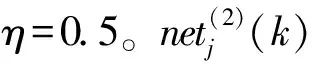
2 仿真分析
2.1 频率与负荷扰动实验结果分析
为验证本文所提出基于BP网络逆控制的水轮机调速系统的可行性,实验建立于Matlab仿真平台,通过在输入r端添加不同幅值阶跃信号来表示系统给定转速值发生变化,加在Mg0端来表示系统负荷扰动,进而进行仿真研究。同时,选取文献[23]中经混合粒子群算法参数整定后的最佳PID值,以及相同稳定工况点的水轮发电机组系统参数进行仿真,进而对2种仿真结果进行比较。具体的系统参数及PID参数值如表1所示。
表1 基本实验参数

参数eqyeqhTweyehTaenKpKiKd值1.230.130.831.400.355.720.458.000.431.33
基于表1中被控水轮发电机组系统的参数进行仿真实验,仿真时间取40 s,空载工况,即Mg0不加任何信号状态下,在输入r端分别加入幅值为0.1、0.05的阶跃信号获取水轮发电机组系统在10%及5%转速频率扰动下分别采用PID控制与BP网络逆控制的控制效果。仿真结果如图6所示。从图6可以看出,系统运行在空载状态时,无论是10%还是5%频率扰动,与PID控制相比,本文的水轮发电机组在BP网络逆控制下系统性能明显改善。被控水轮发电机组系统在BP网络逆控制下系统转速输出响应更稳定地趋于稳态,并且在到达稳态之前,波动较小,且没有PID控制产生的超调量。
同样设置仿真时间为40 s,在系统负荷扰动工况下,系统输入r端信号为0,负荷扰动Mg0端分别加入0.1、0.05的阶跃信号获取水轮发电机组系统在10%及5%负荷扰动下分别采用PID控制与BP网络逆控制的控制效果。仿真结果如图7所示。同样地,从图7可以看出,与传统PID控制相比,水轮发电机组系统在BP神经网络逆控制下,受到负荷扰动后,系统能更平缓地趋于稳态,且消除了系统的超调量,控制效果明显优于PID控制。

(a) 10%频率扰动
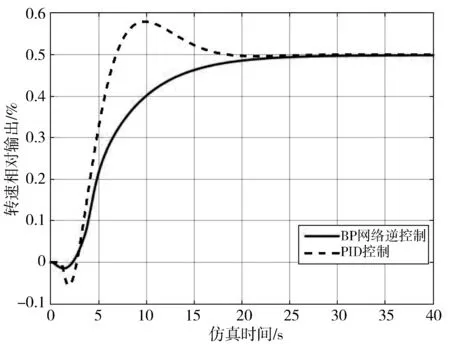
(b) 5%频率扰动
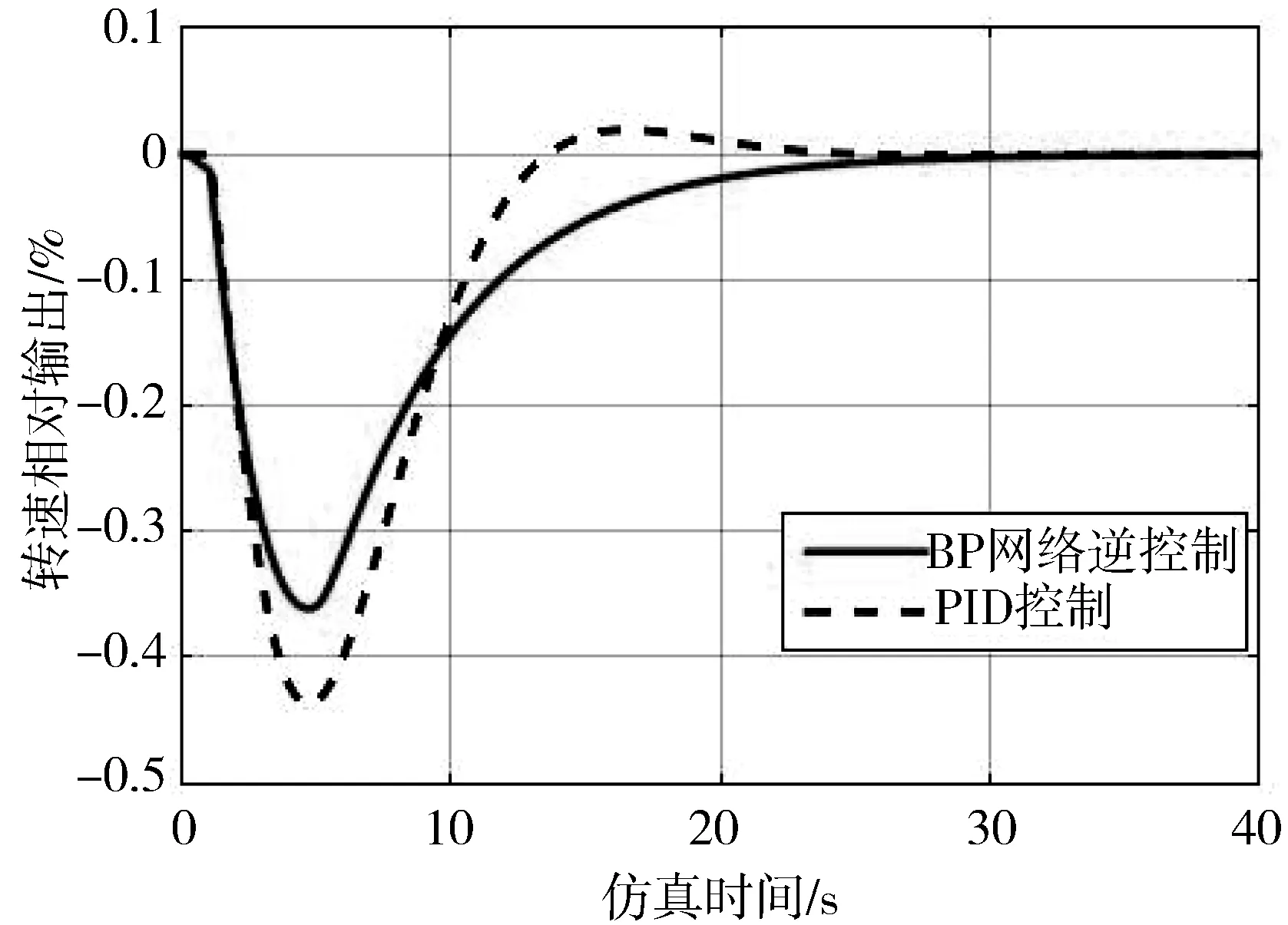
(a) 10%负荷扰动
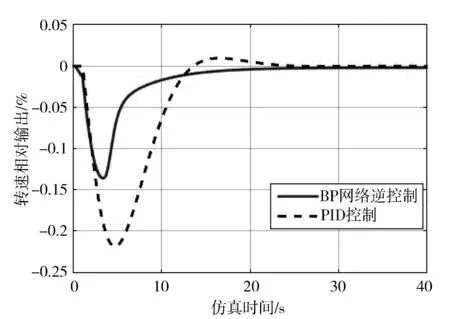
(b) 5%负荷扰动
2.2 系统鲁棒性验证
水轮机惯性时间常数Tw是影响水轮机调节运行工况的主要参数,故为验证本文提出的控制系统具有很好的鲁棒性,需在Tw改变较大的情况下,被控系统响应依然具有较好的动态、静态特性。因此,当Tw=1.8 s时,对系统进行仿真,得到的结果如图8、图9所示。
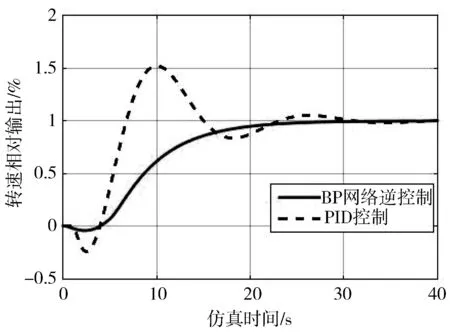
(a) 10%频率扰动
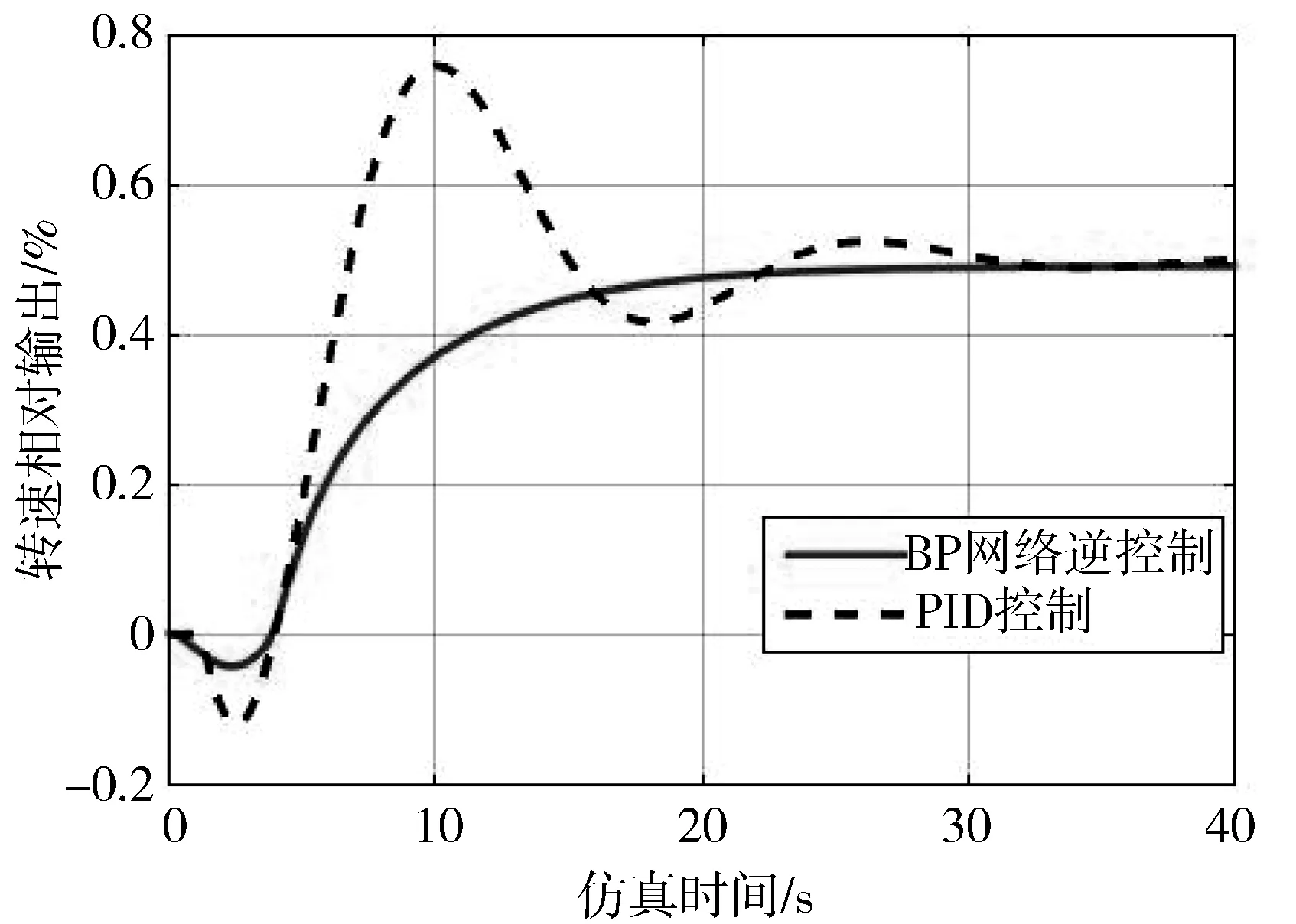
(b) 5%频率扰动
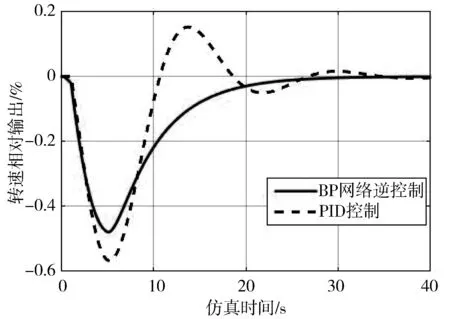
(a) 10%负荷扰动
由图8、图9可以看出,当水轮机惯性时间常数变化较大时,不论是频率还是负荷扰动情况下,PID控制的系统响应特性明显变差,而本文提出的逆控制系统响应除了调节时间略有延长外,其余良好的响应特性均保持不变,从而可以说明本文采用的逆控制算法具有较好的鲁棒性。
3 结束语
本文基于自适应逆控制以及神经网络算法的基本思想,提出了一种水轮发电机组系统的在线自适应逆控制算法,在考虑被控系统中的非线性环节的基础上,针对水轮发电机组系统运行过程中存在的扰动信号,能够及时响应并施加控制,不仅能获得较好的动态特性,控制效果较好,而且具有良好的鲁棒性。本文所提的算法虽然具有一般性,即对具有不确定性、干扰随机的非线性对象的控制提供了一定的解决思路,但该算法较为基础,对于系统响应速度方面的改善效果不大,且此次仿真依赖于文献[23]中的被控系统模型。下一步将从更符合实际工程中的模型入手,用更精确的算法进一步改善控制性能。

