基于改进A*算法的多无人机协同战术规划

张哲， 吴剑,2， 代冀阳， 李品伟

(1.南昌航空大学 信息工程学院, 江西 南昌 330063; 2.北京航空航天大学 可靠性与系统工程学院, 北京 100191)

0 引言

现代空中作战往往需要以多无人机联合作战的方式进行，而采用分层递阶结构的思想来分解问题，是解决多无人机自主协同控制和决策复杂性的有效手段[1]。

战术飞行任务管理系统是先进战机智能化的集中体现。为了合理地对多机作战方式进行安排、实现多机战斗力的倍增，需要对战术飞行任务管理系统进行深入分析。目前大多数研究仅停留在宏观角度进行探讨，如Sutton等[2]提出的多无人机协同控制分层递阶结构，将系统分为3个决策层和1个控制层。文献[3-6]提出集中式系统执行层次结构，任务执行效能不高。这些研究只给出了任务飞行管理系统的某种分层递阶结构。文献[7-11]研究了分布式多机协同层次化关系，将4个层次进行细分，提高了任务的执行效能，进一步优化了各执行层次间的控制结构。文献[12-14]重点讨论了系统任务层和导航层的层次化关系，并将它们作为系统底层，简单地细分为任务分配和航路规划两个方面分别进行研究。

本文提出一种基于改进A*算法的复杂环境下多无人机编队协同战术规划方法，结合分层思想和多机协同控制系统优化流程，以编队成员时间代价和碰撞代价为协同变量，建立多无人机编队协同飞行控制的数学模型，提出作战效能的评估方法；在求解协同作战航路时，针对目前A*算法的不足，提出一种多层变步长搜索策略的改进A*算法，以提高航路搜索效率，保证解的最优性；研究了任务分配方法和资源协调方法，分别利用改进A*算法和传统A*算法进行编队协同作战的对比仿真实验。仿真结果验证了所提改进算法和战术规划方法的有效性。

1 作战规划

1.1 多无人机编队协同战术规划系统流程

从战术规划内容方面，可将多无人机协同战术规划系统分为作战目标确定、态势分析、任务规划、航路规划和弹药规划等内容，该部分可以归纳为决策层和协调层2个层次。进一步分析整个战术规划系统的实现步骤，可以得到多无人机编队协同控制优化系统的流程如图1所示。

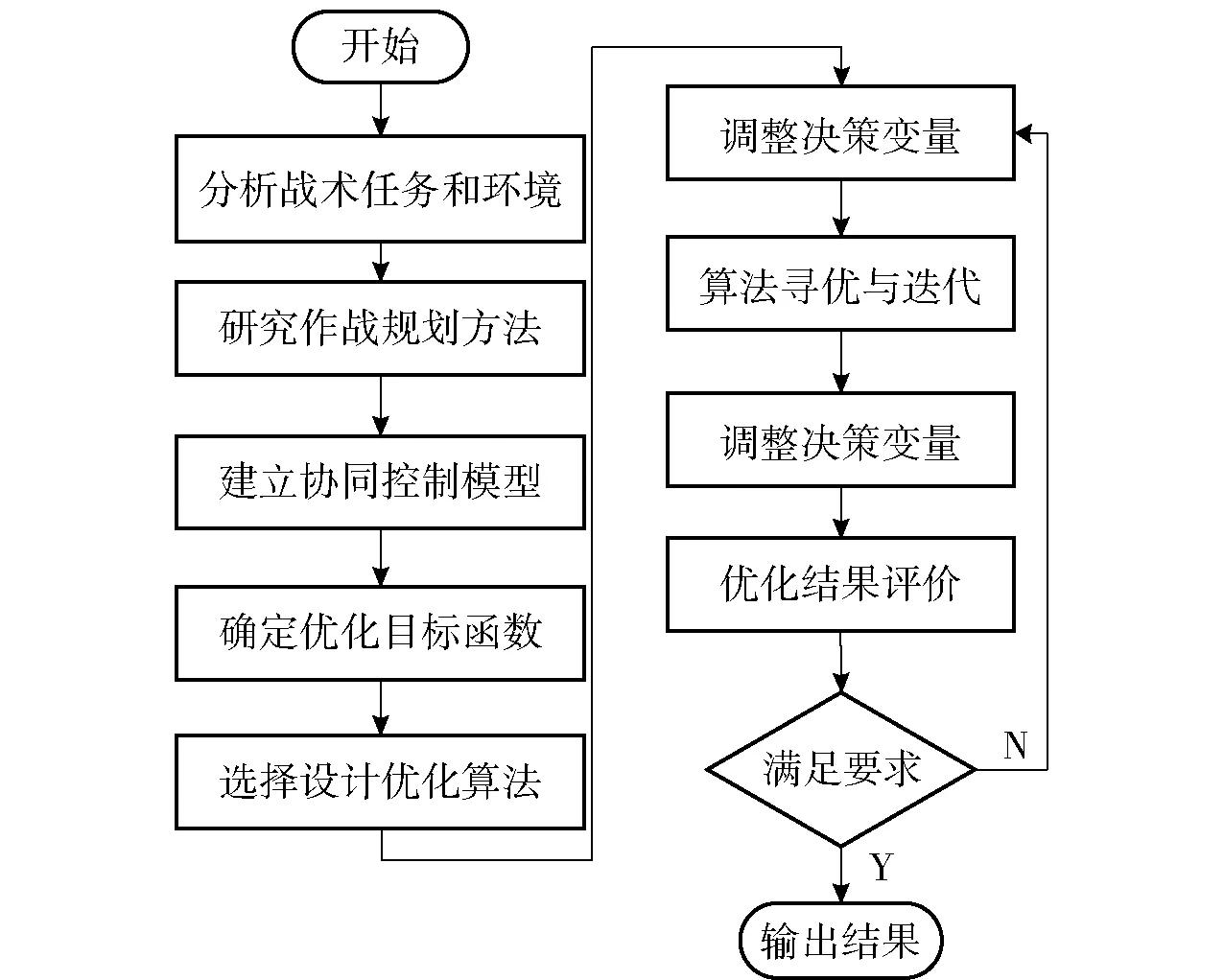
图1 多无人机编队协同控制优化系统的流程Fig.1 Process of formation collaborative control optimization system for UAVs

1.2 离线规划

1.2.1 战役层规划

战役层的规划由地面站或编队内的长机完成。具体包括：1)制定战役目标，并设置主次战役任务的重要等级分别为ring0和ring1；2)获取战场全局态势；3)启动编队战术规划；4)监督编队整体战术规划的结果，内容为编队飞机任务规划和编队弹药规划的总体结果；5)依据战场态势，确定战场的不确定战役目标；6)当所有战役目标都有解决方案且作战飞机载荷都已加载完成时，战役层的规划结束。

战役层规划中的基本要素为任务、平台和决策者，三者之间的关系可用如下3个矩阵表示。

1)决策者- 平台控制矩阵md：

(1)

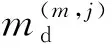
2)平台- 任务匹配矩阵mp：

(2)

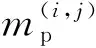
3)任务- 决策者分配矩阵mt：

(3)

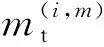
由于时间测度是战役层规划结果的关键性能指标，用于衡量规划的时间效率，因此给出相关数学分析如下：

1)任务完成时间fc. 主要确定第i个任务Ti的开始时间fs和任务处理时间fp，从而得到在战役层每个执行平台上所有任务的完成时间为

(4)

式中：T为子任务构成的集合，T={T1,T2,…，Ti,…，TM}。

2)任务间平均转移时间ft. 该指标是指战役层上各个任务不同发生位置之间转移所用时间的均值。则任务间的平均转移时间为

(5)

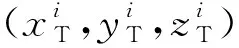
1.2.2 战术层规划

战术层规划由战役规划启动，采用全自动方式进行。规划内容分为以下决策层寻优和协调层寻优两步。决策层寻优表现为作战目标的增补与泛化过程，依据图1中的结构关系可以进一步抽象为图2所示的流程。图2中：①表示由战役目标出发，依据战场态势的变化，经迭代循环后增补一些必要对象为新的作战目标，形成战术目标集；②表示依据战场态势，对潜在的不确定性事件进行评估。

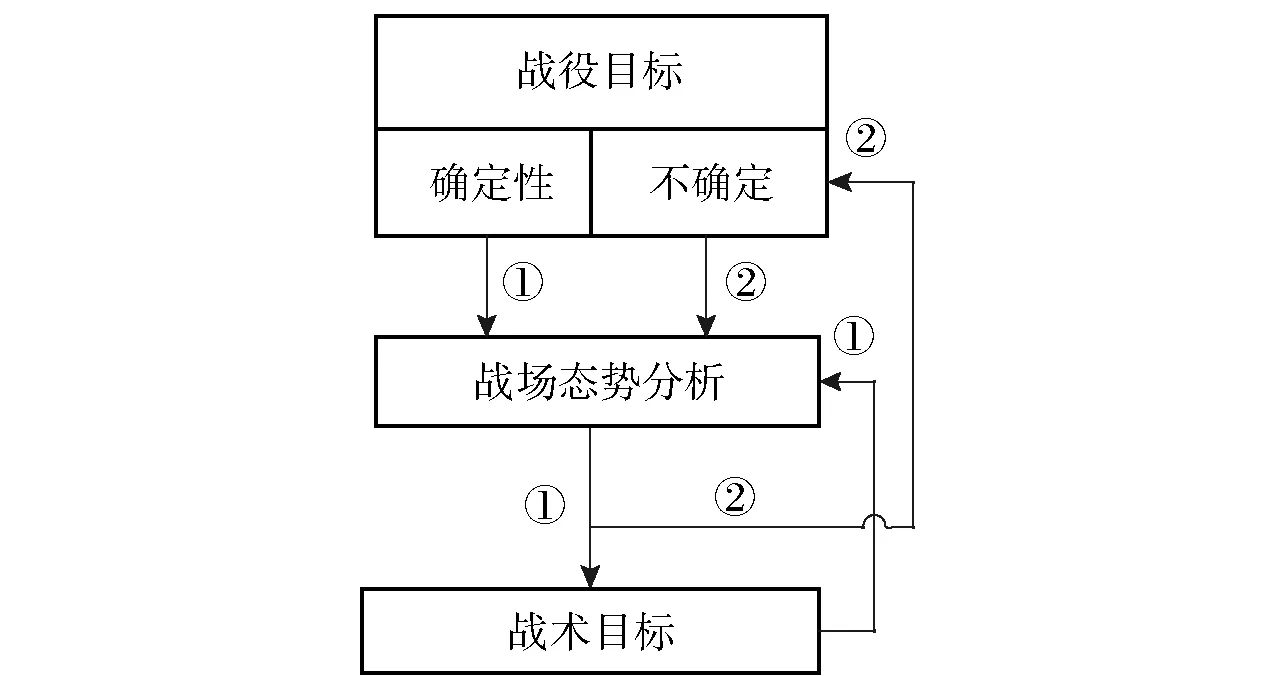
图2 作战目标的迭代优化Fig.2 Iterative optimization of operational objectives

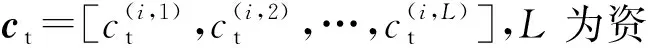
(6)

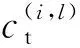
协调层总体分为任务规划和航路规划两个层次，目标在于实现作战资源的协调和优化。以平台利用测度来反映协调层寻优结果，它体现了平台作为直接参与行动的物理资源，包括其资源和时间上性能的好坏。下面给出相关数学描述。

1)平台资源利用率U. 平台的资源利用率是任务规划中平台资源使用情况评价指标。对于∀Pj，其资源利用率为

(7)

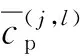
2)平台时间利用率N. 该指标反映了平台执行任务时间占整个任务执行时间段的平均比例。对于∀Pj，其时间利用率为

(8)

1.2.3 离线规划的步骤

步骤1针对主要战术目标的解决方案。依据工事的坚固程度，确定需要使用的弹药资源数量；依据飞机的性能(每次发射多少发弹)，确定打击威胁所需要的总飞机数量；依据威胁的特点，确定提供攻击波次所需要的无人机数量。

步骤2补充掩护任务的解决方案。依据战场态势信息，确定担任掩护任务所需要的弹药和飞机数量。

步骤3补充附加战术目标的解决方案。依据战场态势信息，确定潜在的战场威胁，评估可能新增的作战任务。然后，为可能新增的作战任务确定需要额外携带的弹药和增派的飞机数量。

步骤4对编队内的弹药进行协调。对于不同飞机，采用交换弹药的方法，避免出现某架飞机过多的重要任务，均衡各架飞机的弹药载荷。

1.3 在线规划

当编队处于执行任务中时，需要对编队及编队中各架飞机进行作战行为的监督，并适时做出适度的调整[15-16]。

1.3.1 战役层规划

对于战役层，战场态势信息、弹药信息和编队无人机信息通常都集中于地面站或编队中的长机，因此，战役层在线规划的具体步骤如下：

步骤1依据各种传感器的实时信息，对战场的全局态势进行增补。

步骤2对于突然发生的战场重大态势变化，适时增补或删减战役目标，并设置相应的任务等级。

步骤3启动编队内的在线规划。

1.3.2 战术层规划

对于战术层，当编队协同作战过程中任务、弹药资源或战场环境信息发生改变时，需要进行战术层的在线规划，具体步骤如下：

步骤1针对新增战术目标本身的打击方案。依据战役目标的对象寻找相应的弹药，再由弹药寻找载机。在各个任务级别比当前任务级别低的载机中，寻找打击代价最小的载机执行战术任务。

步骤2采取新增战术目标打击方案替代此前的战术任务，进行任务重分配。

步骤3为新增战术目标打击方案的掩护行动寻找解决方案。

步骤4采取新增掩护行动任务方案替代的此前战术任务，进行任务重分配。

2 多无人机协同作战数学模型

2.1 单架无人机的运动学模型

忽略空气阻力的影响，采用如下质点模型：

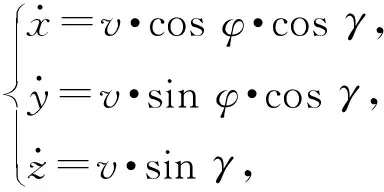
(9)

根据无人机飞行包线的约束，建立以下约束条件：

(10)

式中：φmin、φmax分别为航向角的最小值与最大值；γmin、γmax分别为爬升角的最小值与最大值；Hmin为最低飞行高度。

2.2 编队无人机间的相对运动关系

不考虑天气等干扰因素对编队飞行控制的影响，对无人机编队飞行过程进行研究[17]，建立编队中无人机间相对运动模型为

(11)

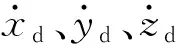
2.3 协同代价分析

2.3.1 威胁代价

在无人机编队飞行过程中，战场环境中的威胁通常为组网雷达系统。对于雷达威胁，无人机在空间中某一位置的雷达探测概率与当前姿态角和自身与雷达位置的相对距离有关。若组网雷达系统中有多部雷达，则当无人机处在雷达探测范围内时会受到雷达多次扫描，累计多次扫描的瞬时探测概率便可得到雷达对目标的发现概率。因此，组网雷达系统对无人机的联合探测概率为

(12)

式中:P为组网雷达探测概率；Q表示系统中雷达的数量；PI表示第I部雷达的探测概率。

2.3.2 协同代价分析

在多无人机编队协同作战中，不仅要考虑无人机受到的威胁代价，还需要考虑多架无人机编队成员之间的时间协同代价以及防碰撞约束条件[18-19]，才能在实现战术规划的目标下保证编队成员间的安全。因此，需要从无人机的时间协同代价与碰撞代价的目标函数两方面进行分析。

对于编队成员间的时间协同代价，建立目标函数为

(13)

式中:Jt为时间协同代价的目标函数；ta为第a架无人机到达指定位置的实际时间；K为无人机的数量；tac为第a架无人机到达指定位置的指令时间。

对于编队成员间的碰撞代价，建立目标函数为

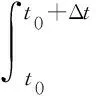
(14)

编队成员间的具体约束条件为

(15)

式中：Rmin、Rmax分别为两架无人机之间相对距离的最小值与最大值；xd，min、xd，max分别为气流坐标系下x轴方向上相对距离的最小值与最大值；yd，min、yd，max分别为气流坐标系下y轴方向上相对距离的最小值与最大值；zd，min、zd，max分别为气流坐标系下z轴方向上相对距离的最小值与最大值；φe，min、φe，max分别为航向角差值的最小值与最大值。

因此，综合考虑无人机的时间协同代价与碰撞代价两方面，采用线性加权指标作为综合编队目标函数，结合实际战场态势确定权重系数取值，可以得到综合目标函数表达式为

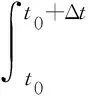
(16)

式中：tr为编队到达时间；ω1、ω2、ω3、ω4为函数的权重系数，分别表示时间最短、威胁最小、指令误差最小和等效碰撞次数最少。

2.4 作战效能分析

2.4.1 攻击收益

在编队协同作战规划过程中，为了保证编队成员的攻击收益最大化，需要在任务分配基础上根据无人机所携带的弹药资源评估目标打击效果。通过分析攻击收益，可以保障充分利用武器弹药载荷，最大化地实现摧毁目标价值。假设每架无人机均携带一定数量的弹药资源，进行如下分析：

1)无人机所携带的弹药资源种类。假设第a架无人机携带的资源向量为Ra={R1,R2,…,RL}。例如Ra={2,0,1}表示第a架无人机装载了第1类和第3类弹药资源的数量分别为2个和1个，没有装载第2类弹药资源。

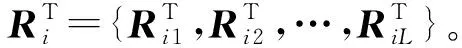
(17)

式中：ATi为任务完成的表征系数，对于某个任务Ti，当前弹药资源的总量大于执行任务所需的弹药量，则所有目标成功被击毁时ATi=1，任务完成，反之ATi=0，任务失败。

3)作战规划总攻击收益。由上述分析可以得到编队协同作战规划过程中的总攻击收益为

(18)

式中：Vi为第i架无人机的攻击收益。

2.4.2 无人机的毁伤代价

当无人机编队协同飞行时，假设第a架无人机执行任务Ti后的生存概率为Pai,则Pai=1-P. 对于编队中的无人机，执行任务时造成的毁伤代价为

(19)

3 A*算法及改进方案

在进行任务和资源的合理分配后，需要为无人机编队设计规划作战时的航路，这时需要利用一些路径规划算法解决问题。A*算法作为一种启发式搜索算法，广泛应用于各类智能体的路径规划问题中。

3.1 算法描述

在标准A*算法的航路搜索过程中，通过设定合适的启发函数，全面估计待搜索区域可扩展搜索点的代价值，比较各点不同代价值的大小，兼顾考虑航迹点搜索的运算时间与距离代价，找出一条最优的航路。在A*算法中，通常利用对OPEN表和CLOSE表的操作实现航迹点的存储和更新。算法的寻优运算可以表示为

f(n)=g(n)+h(n)，

(20)

式中：f(n)为起点到终点的路径代价估值，n为航迹点序号；g(n)为起点到当前航迹点的实际路径代价值；h(n)为当前航迹点到终点的最优路径代价估值。

然而，当A*算法在大规模作战环境中进行航路寻优时，由于航路点搜索数量庞大，传统A*算法的时间代价会随着搜索节点的增加呈现超线性增长，已经无法满足无人机协同作战过程中的实时性要求。因此，有必要对A*算法进行改进，尽可能减少搜索节点的数量，提高航路搜索效率，同时保证解的较优性。

3.2 改进方案

首先，为了提高算法的搜索精度，使待搜索区域的代价更为精确[20-21]，在传统A*算法的(19)式中引入一个加权因子λ，其中λ>1，此时有f(n)的表达式：

f(n)=g(n)+λ·h(n).

(21)

这意味着增大了未知路径代价在总路径代价的占比，即增加了A*算法的搜索深度，防止算法陷入局部搜索的死区中，保证最优解的质量。

然后，为了减少搜索节点的数量规模，通过对A*算法中的OPEN表和CLOSE表的操作，对算法搜索的扩展方式进行改进。

3.2.1 单步扩展的搜索方式

在实际作战航路规划中，对于A*算法需要考虑的要点包括：1)结合飞机方程等物理特性，体现多约束条件下的可飞航路扩展，满足最短直飞距离和最小转弯半径等限制；2)合理的单步扩展，以合理地处理好解的最优与迭代收敛速度之间以及搜索区域广度和分辨精度之间的矛盾[22]；3)实时规划条件下还需要考虑战场下的威胁源限制。

当存在最短直飞距离和最小转弯半径限制时，可以设置A*方法的每步扩展为扇形辐射状扩展，即从当前点E出发，在以最大扩展角αmax的水平扇面内有n+1个扩展点，当扩展范围内存在某个威胁时，无人机从E至H的最优路径如图3所示。图3中，H点为目标点，F为最佳扩展点，G为威胁与目标点在水平方向上的切点。

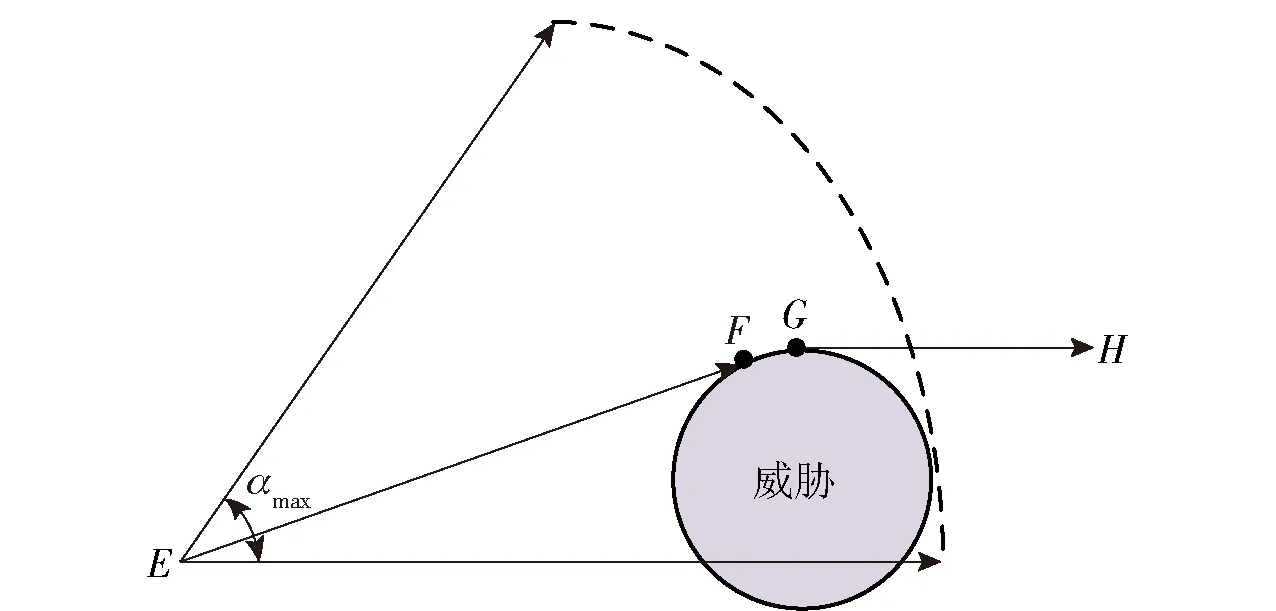
图3 单步扩展Fig.3 Single step expansion

3.2.2 多层变步长扩展的搜索方式

在单步扩展时，若作战地图离散化后的栅格距离很小，则可能造成所得到的航路会部分穿过威胁区域，航路质量不能得到保证。为了解决这一问题，将三维扩展搜索区域划分为具有一定高度的W个扇形平面，在单步扩展方式基础上设计一种多层变步长的搜索策略，如图4所示。图4中，B2q+1,q表示扇形区域中航迹点所在的位置，q表示弧长分段的数量。

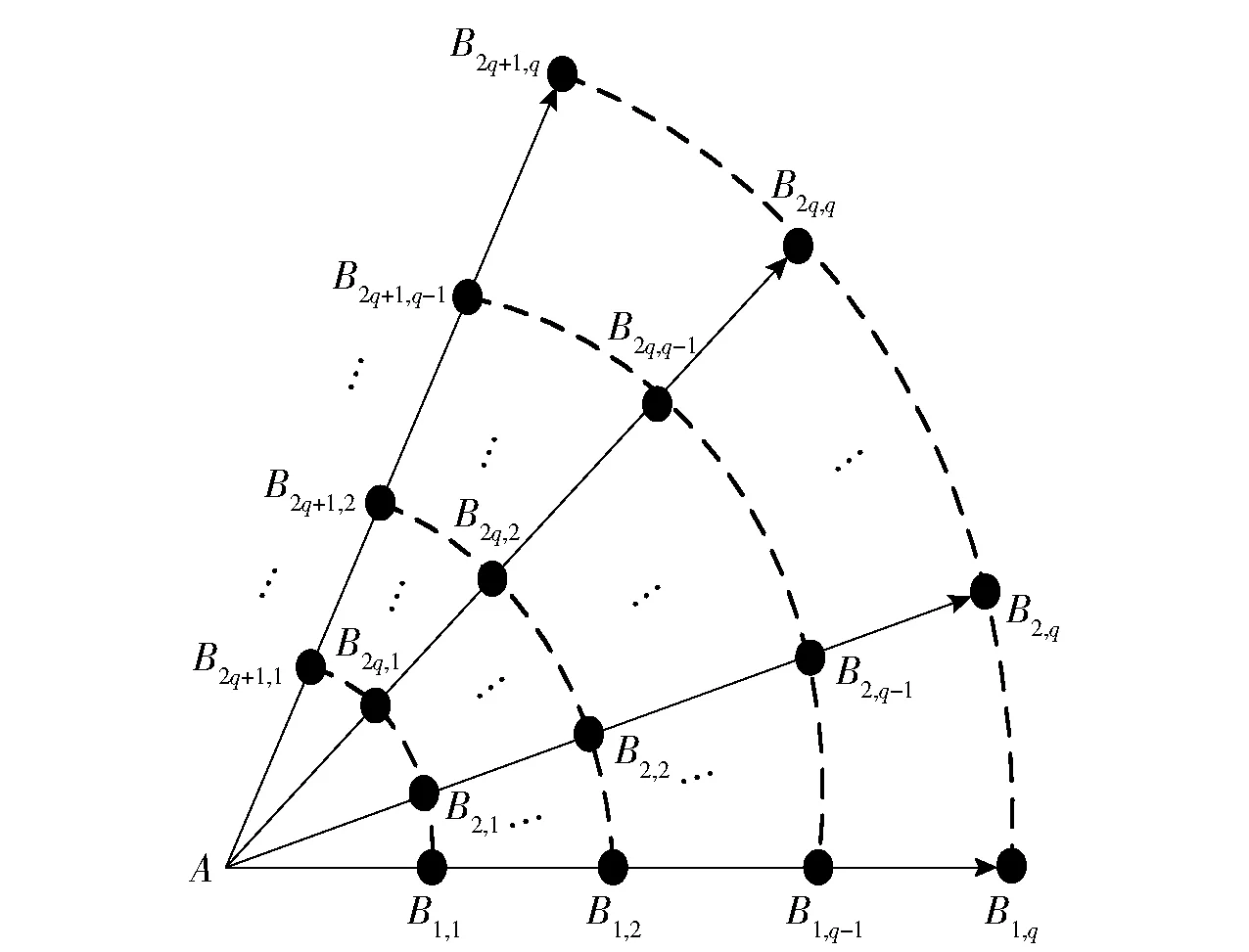
图4 多层变步长搜索方式Fig.4 Multi-layer variable step size search method

由图3和图4可见，当网格间距很小时，最优扩展点F与其邻近扩展点十分接近。若扇面离散化的过程中F未被选中，则可以用其相邻扩展点来很好地逼近F.

在改进A*算法的搜索过程中，第c步的航迹点坐标与第c+1步的航迹点坐标计算公式如下：

(22)

式中：(xc,yc,zc)、(xc+1,yc+1,zc+1)分别为算法搜索第c步和第c+1步的航迹点坐标；αc,n和Lc,n分别为扩展搜索线段之间的夹角与对应的弧长；Lh为扇面的弧长；α0和L0分别为初始搜索角度和对应的弧长。

4 实验仿真分析

假设编队可以调度4架先进无人战斗机(UCAV)，每架无人机可以携带2发弹药，战场态势如图5所示。计算机配置为Intel(R) Core i5-4210M @2.60 GHz，采用Windows10操作系统和MATLAB R2017a软件进行仿真实验。

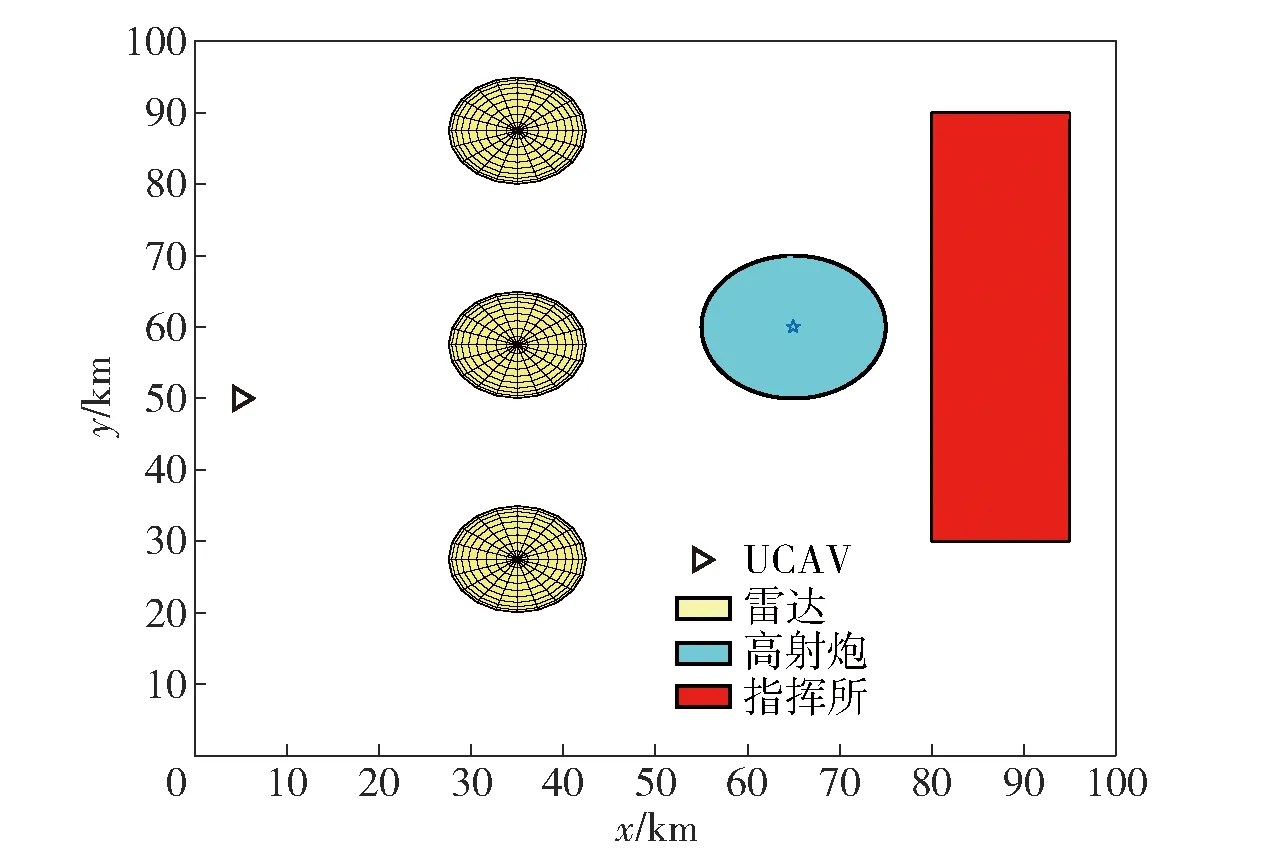
图5 战场态势Fig.5 Battlefield situation

4.1 任务分配

在任务分配的逐次迭代过程中，载机信息和弹药资源的参数变化分别如表1和表2所示。表1和表2中标记出了每次迭代改变了的内容。

下面对表1和表2的结果进行具体分析。第1次迭代：对主要战术目标给出解决方案，表现为UCAV 1和UCAV 2各挂载1发1类弹；第2次迭代：对主要战术目标的掩护行动给出解决方案，表现为UCAV 2和UCAV 3各挂载1发3类弹；第3次迭代：对潜在的可能战术目标及其掩护行动给出解决方案，表现为UCAV 1挂载1发3类弹，UCAV 2挂载1发2类弹，UCAV 3 挂载2发3类弹，UCAV 4挂载1发2类弹和1发3类弹；第4次迭代：对编队载机的弹药进行协调，避免同类弹过于集中，表现为UCAV 3和UCAV 4各挂载1发2类弹、UCAV 1挂载的1类弹变为2类弹；第5次迭代：对同一类弹的任务进行调整，避免挂载同一类弹的某架载机任务压力过于集中，表现为UCAV 2和UCAV 3之间的弹药资源进行了交换。

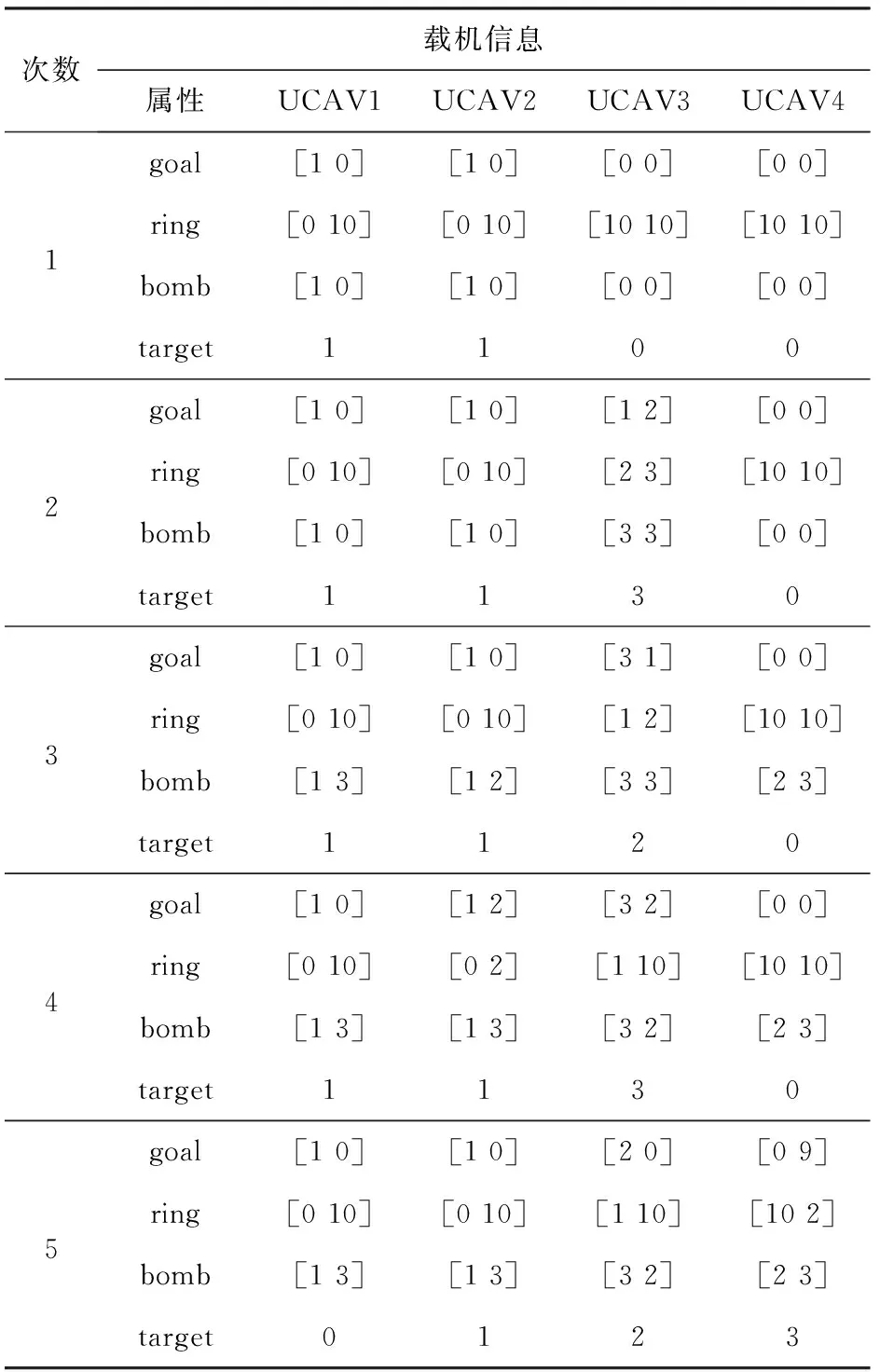
表1 每次迭代中载机信息的变化

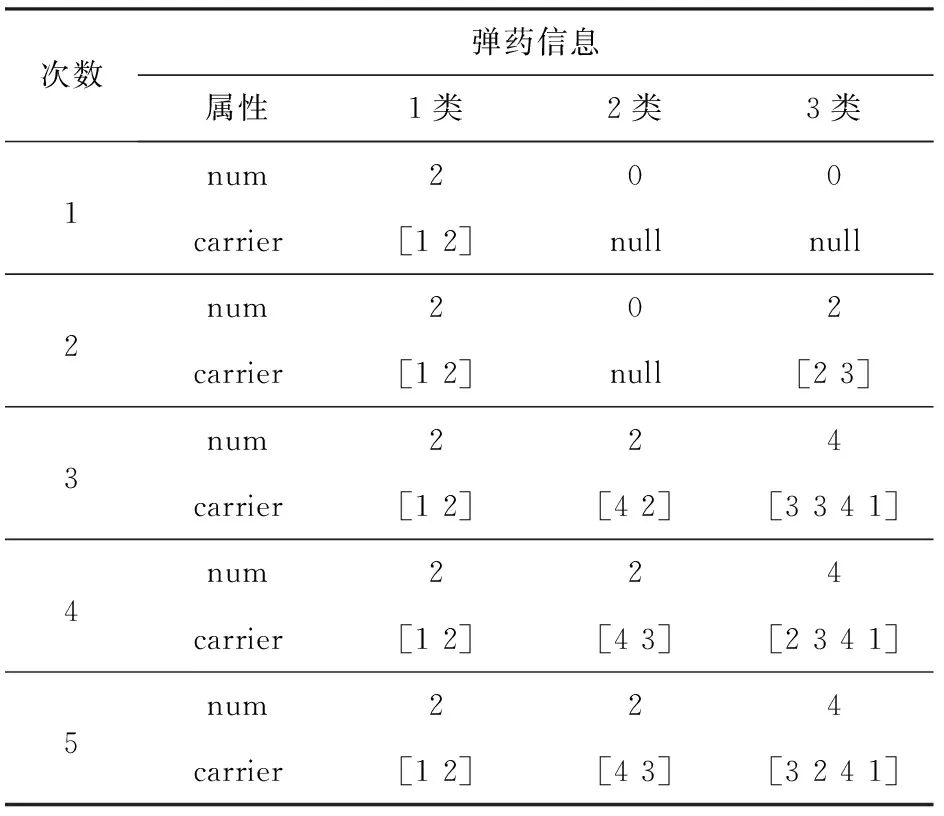
表2 每次迭代中弹药信息的变化

因此，经过5次迭代后，载机和弹药依据任务需求合理地进行了分配。

4.2 作战航路规划

当战斗打响、触发雷达开机时，导致编队飞行途中遭遇雷达威胁。分别采用改进A*算法和传统A*算法进行对比仿真实验，其中：加权因子λ=1.5，最大扇形扩展角度αmax=60°，初始扩展搜索角α0=5°，q=16，W=20，初始步长为2. 计算得到4架无人机协同作战航路如图6和图7所示，作战效能如表3所示，编队无人机的作战资源变化情况如表4和表5所示。

图6 航路规划结果(改进A*算法)Fig.6 Path planning results (improved A* algorithm)

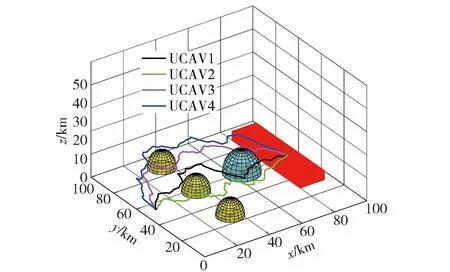
图7 航路规划结果(传统A*算法)Fig.7 Path planning results (conventional A* algorithm)

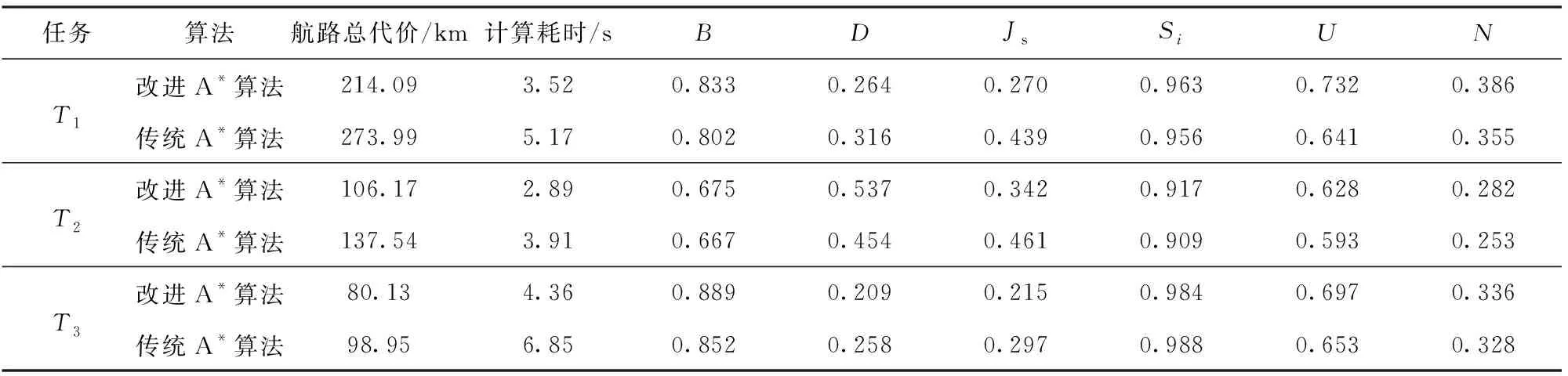
表3 作战效能分析

由于对高射炮的打击行动属于ring0级的掩护任务和ring1级的战术任务，在编队协同打击过程中需要对高射炮的任务进行重分配，重分配结果如表6和表7所示。

由表3可知，在4架无人机协同打击敌方雷达、高射炮和指挥所目标的过程中，利用改进A*算法求解得到的航路在计算耗时和航路代价方面均优于传统A*算法所求解得到的结果，提高了航路搜索的效率，验证了改进A*算法在三维空间下多机协同作战规划问题中的有效性。在作战效能方面，编队无人机之间能够较好地实现协同作战，任务完成精度均在90%以上，完成质量较高。对目标的总攻击收益在80%以上，毁伤代价相对较低，平台资源利用率也基本保持在60%以上，整个编队协同作战过程中资源分配合理，能够有效地摧毁目标。

图8所示为改进A*算法寻优能力分析。由图8可知，寻优能力可以具体表现为航路的总代价、扩展搜索的航迹点总数和航路的折点数，体现了航路的最优性、算法的搜索效率和飞行性能约束。分别对比λ的3种取值对结果的影响，λ=1时实际上为传统A*算法，λ>1时为改进A*算法，λ=1.5时改进A*算法得到的航路达到最优，与传统A*算法相比，进一步表明了改进A*算法具有较好的寻优能力。

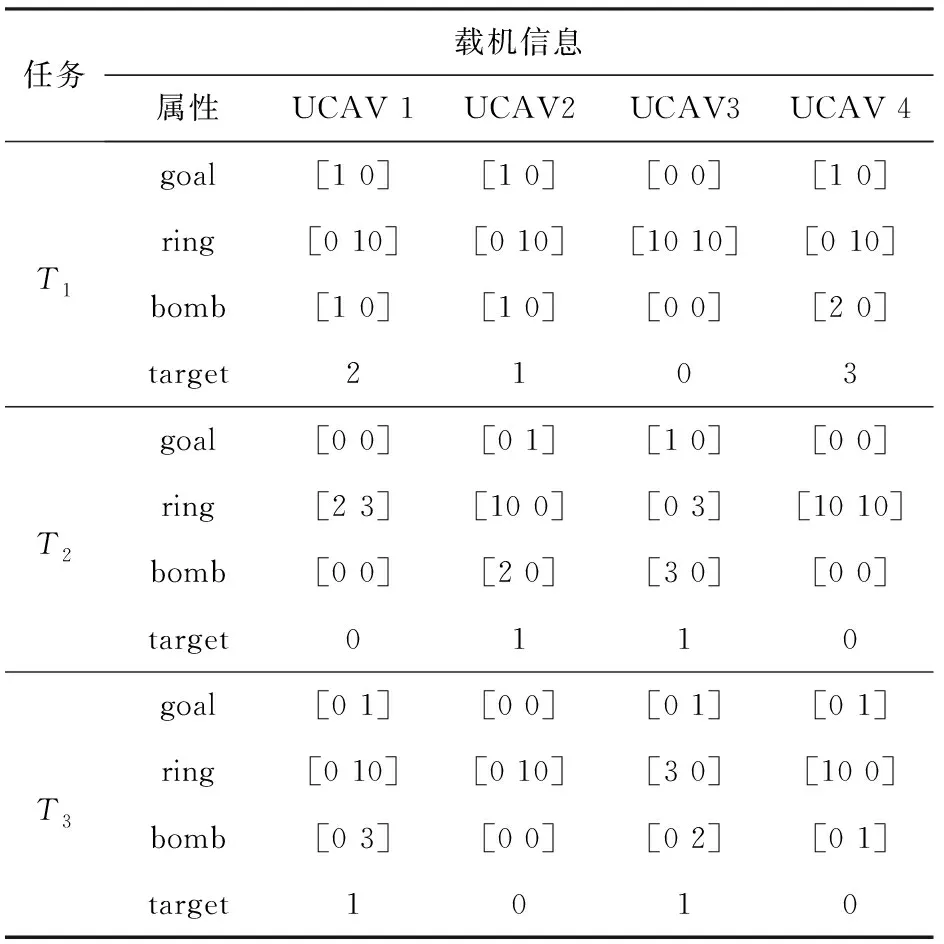
表4 无人机协同作战过程中的载机信息

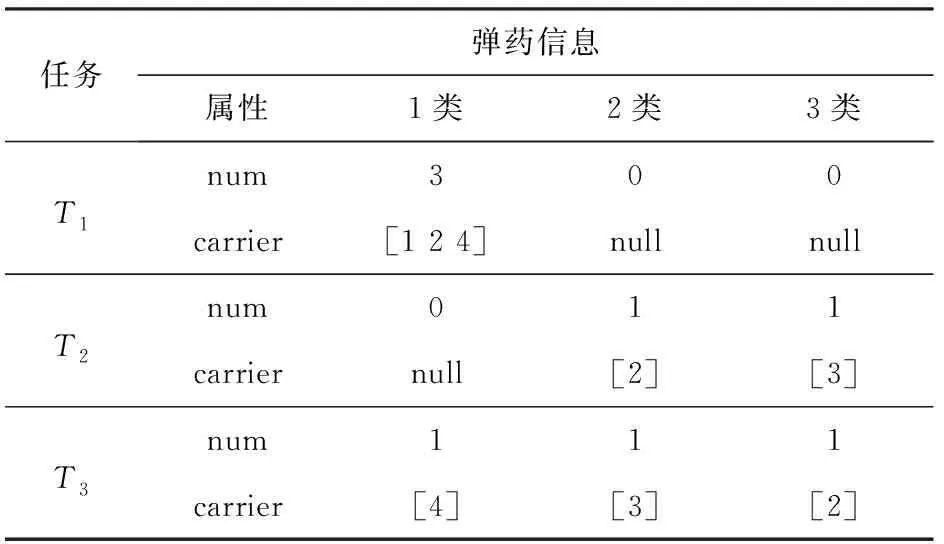
表5 无人机协同作战过程中的弹药信息

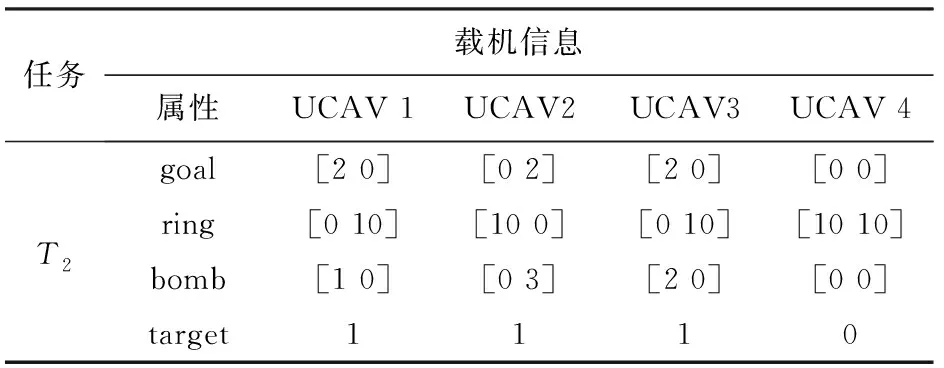
表6 重分配过程中的载机信息

5 结论

本文提出了一种基于改进A*算法的多无人机协同战术规划方法，用于实现高效地任务分配、资源调度，提高系统整体的作战效能。得出以下主要结论：

1)与传统A*算法相比，改进A*算法在对作战航路求解时具有更好的寻优能力，结合单步扩展方式和多层变步长搜索策略，提高了航迹点的搜索效率，航路总代价减小了21.57%，搜索航迹点总数减少了46.35%，航路的折点数减少了81.81%.

2)基于战场态势，使用战役层和战术层的作战目标迭代优化方法能够实现4架无人机之间任务和资源的合理分配与调度，保障各个作战任务能够顺利执行。

3)编队无人机能够较好地完成协同打击雷达、高射炮和指挥所的作战任务，获得了较高的攻击收益，从而实现了作战效能的最大化。与传统A*算法相比，验证了本文方法的有效性。

未来战场环境将存在各种不确定的威胁，本文方法对于动态威胁的适用性有限，如何在有移动目标威胁的复杂环境下实现多无人机协同作战，是今后的主要研究方向。