基于樽海鞘算法的PID参数优化

刘亚飞，郝玉然，韩超杰

（1.华北水利水电大学 电力学院，河南 郑州 450000；2.郑州地铁集团有限公司，河南 郑州 450000）

0 引 言

PID控制由于结构简单、有效性高、控制效果较好、鲁棒性强以及可靠性高，广泛应用在工业领域。有很多方法可以调整PID控制器参数，如手动调整Ziegler-Nichols法、科恩-库恩调整法以及Z-N阶跃响应法，但手动调整存在一定的局限性。随着智能算法的不断提出，智能算法优化PID参数取得了较好的结果。遗传算法（Genetic Algorithm，GA）[1,2]、粒子群算法（Particle Swarm Optimization，PSO）[3-5]、蚁群算法（Ant Colony Optimization，ACO）[6]、人群搜索算法（Seeker optimization Algorithm，SOA）[7-9]、萤火虫算法（Firefly Algorithm，FA）[10]以及果蝇优化算法（Fruit Fly Optimization Algorithm，FOA）[11,12]等，在优化PID控制器参数中使系统取得了较好的稳态特性和性能指标。

2017年，Seyedali等人通过模拟樽海鞘在海洋航行和觅食时的群集行为，提出了樽海鞘群算法（Salp Swarm Algorithm，SSA）[13]。在多个数学优化函数上对算法进行测试，观察并验证了它们在寻找优化问题最优解时的有效行为。

鉴于樽海鞘群算法简单易行、收敛快以及计算量小等特点，本文提出将该算法优化不稳定系统PID控制器的参数结果与粒子群算法（PSO）优化结果进行比较。

1 PID控制器

控制系统中有PID控制、滑模控制以及鲁棒控制等控制方法。PID控制是工业领域最常见的控制，是一种线性控制器。它根据输入值r(t)与输出值y(t)的误差e(t)控制系统，其中误差e(t)为：

PID的控制规律u(t)为：

式中，Kp、Ki以及Kd为系统误差的比例系数、积分系数以及微分系数，τ为积分变量。

2 樽海鞘算法

樽海鞘是一种生活在海洋深处、身体透明、形状类似水桶的海洋无脊椎动物。它的运动方式与身体构成都与水母十分相似，主要依靠吸收身体周围的水产生动力。不同于大多数群居生物，樽海鞘由于其自身结构，分布形式并非以“群”而是以“链”的形式首尾相连，后一个追随前一个的形式移动。

这条链分为领导者和追随者两组。领导者在链的开始处占据位置，而其余的樽海鞘是追随者。在SSA的数学模型中，领导者的位置更新使用方式为：

式中，xi1表示领导者在第i维中的位置；Fi为食物源在第i维中的位置；ubi、lbi为第i维的上、下边界；c1、c2、c3为随机数。

c1是平衡探索与开发的重要参数，数学定义为：

式中，t为当前迭代；T为最大迭代次数；c2和c3是生成的[0，1]内的随机数。更新追随者位置的方式为：

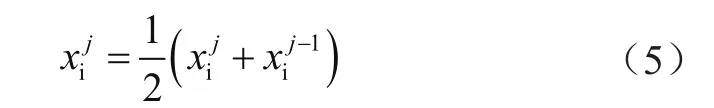
式中，j≥2；xij表示第j个追随者在第i维中的位置。

运算迭代过程一般情况下都需要设置两个门限值充当迭代终止条件。两个门限值中，一个为最大迭代次数，另一个是适应度门限。算法对目前的最优适应度同提前设置好的门限适应度作比较，当其大于门限适应度时终止循环，输出当前最优适应度值对应的坐标值用于充当目标位置的估计值。当最优适应度始终都未达到其门限值时，看迭代次数是否达到设置好的最大迭代次数，如果达到则输出整个迭代过程中适应度最优位置的点坐标作为目标位置的估计值。

3 仿真测试

3.1 实验平台

实验搭建的运行环境为Windows 7、3.20 GHz处理器、8 GB内存，所有算法代码均用Matlab 2016b编程实现。

3.2 目标函数的选取和控制对象

本文选取ITAE指标作为算法的目标函数。ITAE的定义为：

为了验证提出的算法IMFO的可行性，选择不稳定系统进行控制，并分别与使用PSO、MFO与该系统PID控制器参数整定结果对比。

不稳定系统拉普拉斯变换（Laplace Transform）为：

式中，s为复频率。Simulink下的系统模型如图1所示。

3.3 仿真结果

利用PSO、SSA算法对该系统进行仿真，得PSO、SSA优化适应度函数曲线和系统阶跃响应输出曲线分别如图2和图3所示。独立运行50次PSO、SSA算法，得出控制系统优化结果，并记录50次得到的适应度函数值，分别得到适应度函数的平均值、标准差、中值、最好值以及最差值，如表1所示。

图1 PID控制仿真模型

图2 适应度函数控制曲线

图3 算法优化后的系统阶跃响应

表1 算法评价指标

由图2适应度函数控制曲线可知，SSA算法比PSO算法收敛速度快、精度高，易找到全局最优解。从阶跃响应输出曲线来判断，PSO算法平稳时间较长，超调量较大。SSA算法相对于PSO算法，算法控制精度高、收敛快，证明了本文算法的有效性和优越性。通过表1中50次运行结果可以看出，SSA比PSO具有更好的优化结果，算法鲁棒性较好。

4 结 论

为了进一步优化PID参数，本文提出樽海鞘算法（SSA）对PID控制器进行参数优化，通过不稳定系统仿真验证了该算法的有效性和优越性。通过与PSO算法对比可知，SSA算法具有更高的控制精度和鲁棒性，能够为系统PID参数优化提供可靠依据，可使工业控制领域中系统收敛到最优状态，具有广阔的应用前景。