非参数化迭代学习控制的列车自动驾驶控制算法
何之煜,徐 宁
(中国铁道科学研究院集团有限公司 通信信号研究所,北京 100081)
列车自动驾驶(Automatic Train Operation, ATO)技术因其能够实现精准控车、节能运行、提高旅客舒适度和提升路网运输效率等优势,已成为未来智能高速铁路的重要组成部分[1],但由于高速列车实际运行环境复杂多变,不易建模,对自动驾驶控制算法的研究带来了困难。
针对列车自动驾驶控制问题,国内外的专家学者展开了大量的研究工作,主要是从模型构建、误差处理和容错控制这三方面展开研究。在模型构建方面,PID控制模型是最早应用于列车自动驾驶系统中的,利用比例、积分、微分三项线性组合输出控制量[2],但是存在列车运行状态出现暂态和舒适度不足等问题。误差处理是对列车跟踪误差进行非线性变换,从而输出指导列车运行的控制信息,模糊控制利用优秀司机驾驶经验设计模糊规则和隶属度函数,对系统跟踪误差进行模糊推理,从而实现列车的跟踪控制[3],但是存在模糊规则多、模糊推理过程复杂等问题。滑模变结构控制通过设计控制律,使系统跟踪误差在滑模面上下不断抖振,虽然滑模控制具有鲁棒性的优势,但是跟踪误差却无法收敛到零。随着智能控制技术的发展,预测控制[4]、神经网络控制[5]、H2/H∞控制[6]、小波滤波[7]等方法也被引入ATO控制算法的研究中。文献[8-9]等综合考虑列车阻力模型参数时变、传感器故障等情况,设计基于多目标控制的鲁棒容错控制器,从而保证列车在故障状态下仍能跟踪轨迹运行。
上述列车自动驾驶控制算法的研究都是基于跟踪误差反馈的思想来设计的,而高速列车每天同一时间,从同一站点出发,经过相同的距离和运行环境,准点到达目标站点,本质上具有高度重复性的特征。迭代学习控制(Iterative Learning Control, ILC)是针对受控系统运行具有高度重复性特征提出的,它的核心思想是根据上一次迭代的跟踪误差来修正受控系统当前的输入量,从而逐渐逼近期望曲线。目前,ILC已广泛应用于现代工业控制领域,例如工业机器人、注塑机、感应电动机、数控机床等[10-12],而在列车自动驾驶控制方面,文献[13]首次关注到列车运行高度重复的特点,在列车自动驾驶控制的研究中引入迭代学习控制的思想,但是没有对时域上的阻力进行建模,忽略了时变外部扰动对列车控制的影响。文献[14]设计了前馈-反馈控制器,同时利用列车自动驾驶系统的重复性特征,通过处理外部时变扰动影响,实现对期望轨迹的精确跟踪,但是由于其迭代域和时域的PID型线性组合的控制律,不符合列车自动驾驶系统非线性、快时变的特点。文献[15]将列车运行过程中的等效阻力近似为线性函数,但是存在模型失配的问题。文献[16]以列车运行阻力模型为研究对象,基于递推最小二乘法对其经验模型系数进行在线辨识,但是由于列车运行环境的多变性和复杂性,无法建立精确的阻力模型。
本文针对高速列车自动驾驶系统快时变、非线性的特点,以及列车在实际运行过程中难以建模的问题,提出了基于径向基(Radial Basis Function, RBF)的模糊神经网络算法(Fuzzy Neural Network Algorithm, FNNA),将阻力参数视作未知模型参数,利用神经网络算法对非线性映射良好的逼近能力和模糊推理过程对跟踪误差良好的自适应处理能力,实现对运行阻力的渐进逼近。考虑时域和迭代域上二维的跟踪误差,设计基于迭代学习控制的差分-微分型参数更新律,通过计算机仿真验证列车自动驾驶控制算法的跟踪性能。
1 非参数化模型构建
为方便描述,建立列车非参数化动力学模型为
( 1 )
式中:i为迭代次数;s(t)和v(t)分别为列车运行的距离和速度,km和km/h;f(xi,t)为未知非线性函数,表示列车遇到的阻力等效模型,N/kg;xi为列车的状态向量,xi=[sivi]T;b(t)为系统输入的增益;u(t)为系统的控制输入,kN;d(t)为列车运行中的外部随机扰动,N/kg。
为了逼近列车实际运行中的阻力参数,对式( 1 )中的等效模型f(xi,t),构建基于径向基的模糊神经网络算法来实现。算法原理见图1,将RBF模糊神经网络算法设计为包括输入层、隐层和输出层的三层前向网络,其中,隐层是用模糊推理过程来实现对系统状态信息的自适应处理。

图1 RBF模糊神经网络算法原理
整个算法实现的基本流程如下:
Step1输入层节点输入系统的状态信息,也作为模糊推理过程的输入参数。
Step2利用基函数对系统状态信息进行处理,并进行模糊化。
Step3通过预先设定好模糊规则对系统状态信息进行模糊推理。
Step4通过线性加权的计算方式,将算法结果输出到输出层节点。
( 2 )
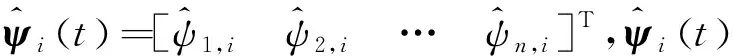
利用高斯基函数对系统状态进行模糊化处理,定义第j条规则的参数为
( 3 )
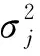
上述的算法中的模糊处理过程主要在模糊神经网络模型的隐层中进行,其中,模糊规则可以表述为
rulej: ifx1,iisG1,jandx2,iisG2,j, thenyiisPj
x1,i和x2,i分别为受控系统的状态量;yi为系统的控制输出;G1,j、G2,j和Pj分别为模糊算法中的输入输出模糊规则。
( 4 )
式中:εi(t)为模糊神经网络的逼近误差,|εi(t)|≤ε*。
因此,非参数化列车动力学模型式( 1 )可以改写为
( 5 )
为便于对所设计的控制器的收敛性证明,对受控系统作出如下假设。
假设1:受控系统在每次运行过程时,具有相同的初始状态,即
xi(0)=xd(0) ∀i∈Z+
( 6 )
式中:xd为列车期望运行轨迹的状态。
假设2:对于列车动力学模型式( 5 ),列车在有限时间t∈[0,T]内,存在一个最优的输入序列,可以控制列车完全跟踪期望轨迹,即系统控制具有可达性,其中,T为列车区间运行时间。
假设3:列车在运行过程中受到的外部随机扰动d(t)是有界的。
2 控制器设计
定义系统的跟踪误差为ei(t)=vd(t)-vi(t),则系统在第i次迭代的误差动态可以描述为
f[xi(t),t]+di(t)+ε(t)}
( 7 )
根据确定性等价原则,可以设计如下控制律为
( 8 )

基于迭代学习控制理论,同时考虑迭代域和时域的跟踪误差,设计差分-微分型参数更新律为
Ψ-1=[0 … 0]T∀t∈[0,T]
( 9 )
κ-1=0 ∀t∈[0,T]
(10)
式中:γ1和γ2分别为参数更新的权重系数,γ1,γ2∈[0,1];β1和β2分别表示参数学习增益,β1,β2>0。
在式(8)中可以看出,控制律包括三个部分:①在采样点上计算得到的系统等效牵引控制输入;②利用RBF模糊神经网络算法得到的非线性阻力函数f(xi,t);③由于外部随机扰动和模型估计误差等因素产生的反馈控制项。
3 收敛性分析
定理1是收敛性证明的主要结果。
定理1:当受控系统式( 5 )在同一区间重复运行时,根据系统控制律式( 8 )和系统参数更新律式( 9 )、式(10),在第i次迭代时,跟踪误差随迭代域逐渐收敛到零。
证明:构造如下复合能量函数
(11)
式中:δΨi(t)为权重估计的差分;δκi(t)为扰动项估计的差分。
下面将证明过程分成两部分,第一部分是证明Ei(t)的差分负定性,第二部分是证明Ei(t)的有界性。
第一部分:复合能量函数Ei(t)的差分负定性
(12)

然后,在迭代域上对能量函数进行差分,可得
ΔEi=Ei-Ei-1=
[δκi-1(t)]2}-Vi-1=
ΔVi+ΔWi+ΔNi+ΔQi+ΔPi
(13)
对上式第四项进行求解,可以得到
(14)
将参数更新律式( 9 )代入式(14)第一项中
(15)
同理,对式(13)的第5项进行求解,可以得到
(16)
根据式(15),将参数更新律式(10)代入上式第一项中,得到
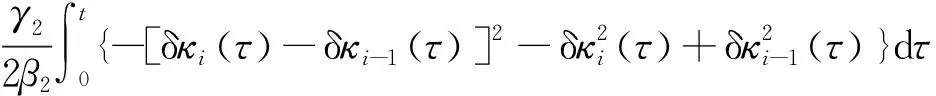
(17)
在复合能量函数表达式(13)中代入式(14)~式(17),可得
ΔEi=ΔVi+ΔWi+ΔNi+ΔQi+ΔPi=
δΨi-1(τ)]T[δΨi(τ)-δΨi-1(τ)]dτ-

(18)
将Lyapunov函数求导结果式(12)代入式(19)中
[δΨi(τ)-δΨi-1(τ)]T[δΨi(τ)-δΨi-1(τ)]}dτ-

[δΨi(τ)-δΨi-1(τ)]dτ-
(19)
由于Lyapunov函数Vi-1具有正定性,因此可以得到
[δΨi(τ)-δΨi-1(τ)]dτ-
(20)
第二部分:复合能量函数Ei(t)的有界性
由上式得到的ΔEi≤0,可以证明在迭代域上,Ei(t)具有差分负定性,那么需要证明其具有有界性,只要证明初始态E0(t)是有界的。令i=0,并对E0(t)在时域上进行求导,可以得到
(21)
将式(15)和式(17)分别代入式(21)中,可得
(22)
由于Ψ*和κ*都是已知区间内的有界连续函数,因此,一定存在已知上边界U*,得到

(23)
那么,可以将E0(t)表述为
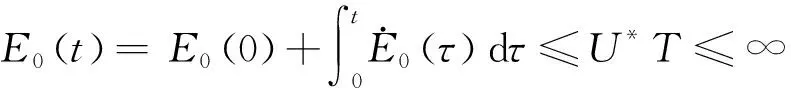
(24)
根据Ei(t)的差分负定性,可以将系统在第i次迭代的复合能量函数表示为
(25)
对式(25)两端取极限
(26)
由于能量函数Ei(t)正定的,且E0(t)有界,根据级数收敛条件,可以得知当i趋于无穷大时,有
(27)
即系统跟踪误差随迭代域逐渐收敛到零。
4 算例仿真
本节内容将对非参数化模型的列车自动驾驶控制算法的性能进行仿真验证。仿真基于CRH-3型车进行,仿真线路长度为69.4 km,运行时间为1 200 s,系统采样时间为1 s,最大制动力为0.8 N/kg,时变外部扰动在[0, 0.01]N/kg中随机产生,系统状态量测误差服从ηc∈N(0,0.002 )。图2给出了列车运行期望轨迹曲线。
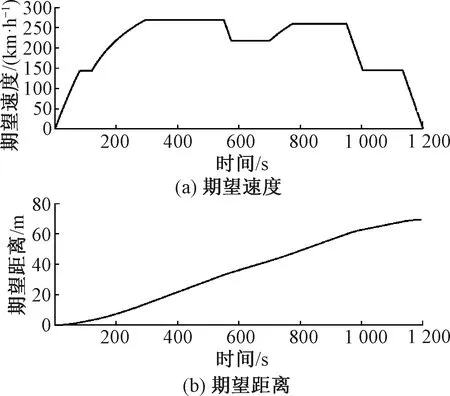
图2 列车期望轨迹
为了方便比较算法的性能,将PID反馈控制和P型迭代学习控制算法与非参数化迭代学习控制算法在收敛性和跟踪精度上进行比较。
方案一:PID反馈控制器
PID控制律设计为
(28)
式中:PID控制算法增益选择经优化后分别为kp=40,ki=6,kd=15。
方案二:P型迭代学习控制器
控制律设计为
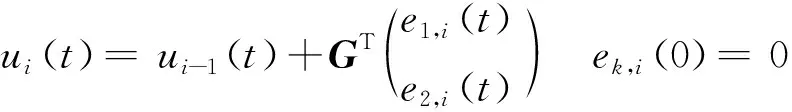
(29)
式中:G为算法的学习增益,G=[g1g2]T,取g1=4,g2=0.8。
方案三:非参数化的迭代学习控制器
根据式( 8 )~式(10)所设计的控制律和参数更新律,给出算法的详细参数:系统模糊规则数设置为5,表示为{负大(NB),负小(NS),零值(ZO),正小(PS),正大(PB)},如表1所示,给出了关于列车运行状态信息的模糊规则表,权值向量初始值设置为Ψ0=[0 0 … 0]T∈R1×25,基函数中心向量选取为[-1 -0.5 0 0.5 1],方差选取为0.05,选取γ1,γ2=0.99为参数更新律式( 9 )~式(10)的权重系数,学习增益β1=16,β2=0.4。
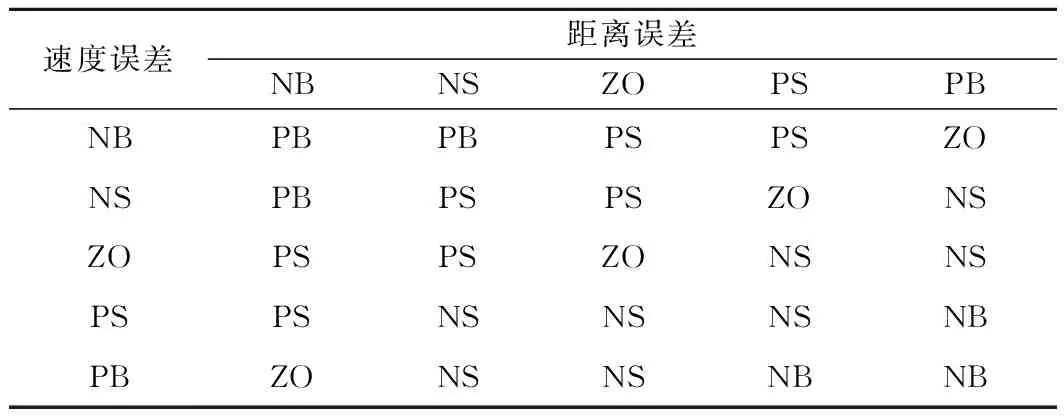
表1 模糊规则表
图3分别给出了方案一~方案三中控制算法对于期望轨迹的跟踪曲线对比。可以得出以下结论:在图3(a)的PID反馈控制跟踪曲线中,当列车由牵引或制动工况变为巡航工况时,列车运行曲线上会表现出较大的暂态,导致列车在一定时间内偏离期望轨迹运行;在图3(b)的P型迭代学习控制跟踪曲线中,其算法的收敛速度较慢,运行曲线偏离轨迹较多;而本文提出的非参数化迭代学习控制算法,通过基于RBF的模糊神经网路算法对阻力模型的逼近,使运行曲线能够快速收敛到期望轨迹附近,从而实现高精度的跟踪。
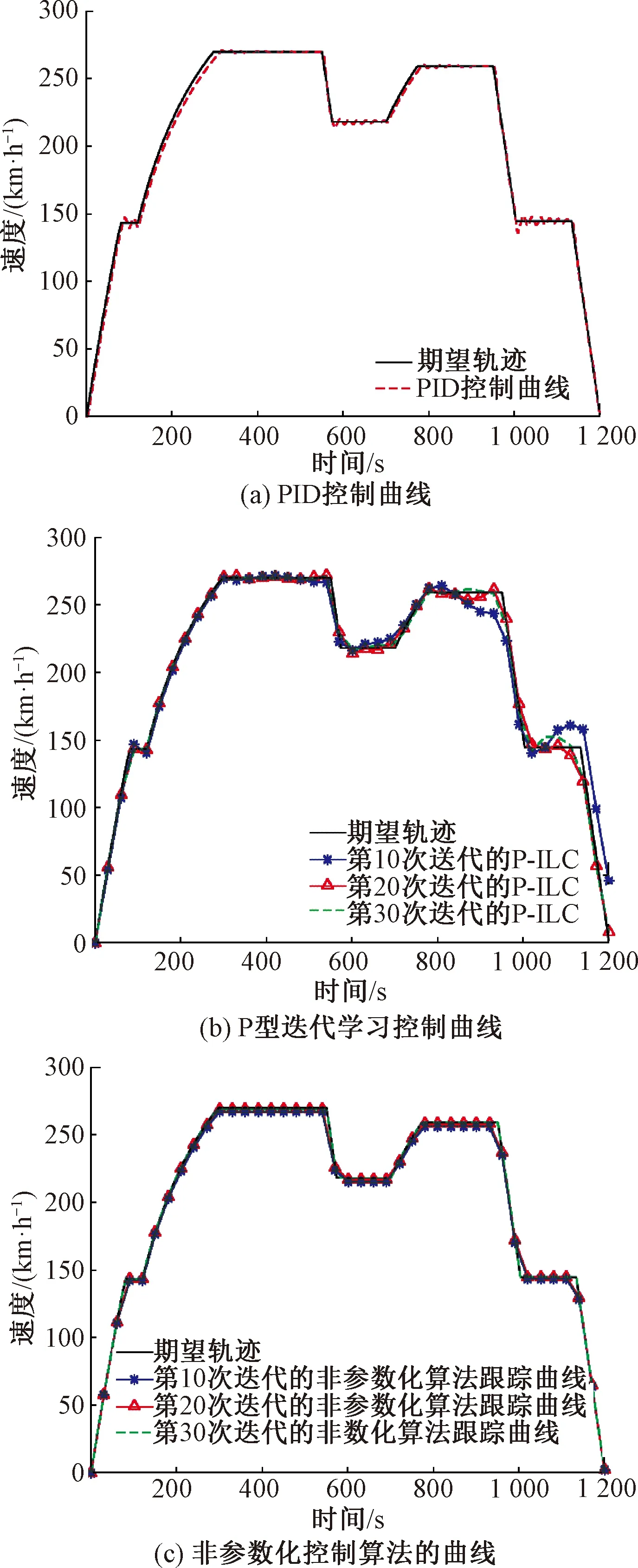
图3 不同算法对列车期望轨迹的跟踪曲线

表2 三种算法跟踪距离和速度对比
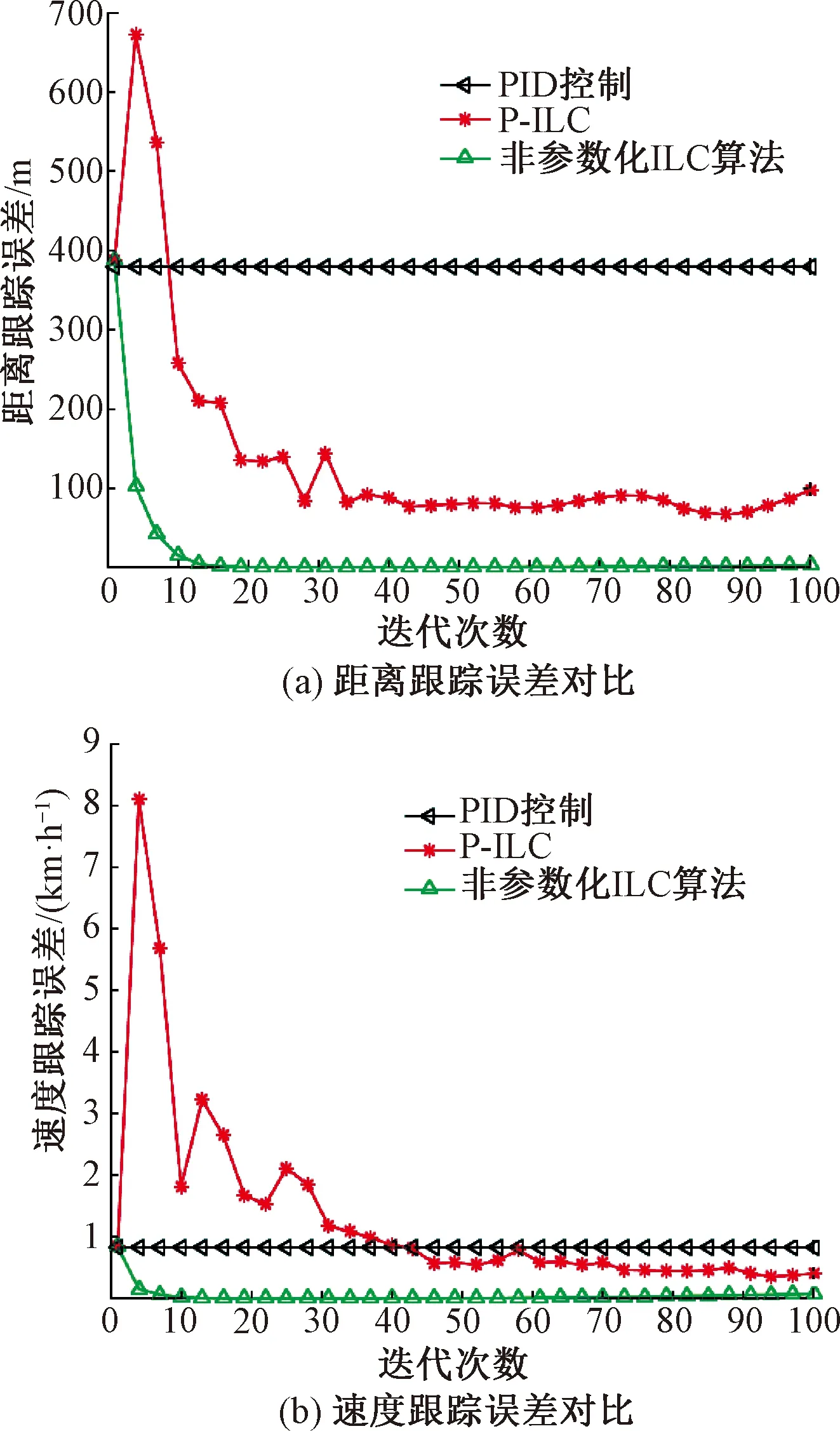
图4 三种算法的跟踪性能对比
图4和表2给出了PID反馈控制、P型迭代学习控制和非参数化迭代学习控制三种算法对跟踪距离和跟踪速度误差在迭代域上的对比,性能对比采用均方根误差来表述。可以看出,PID控制由于只有根据跟踪误差的反馈控制,而没有学习机制,因此跟踪误差无法随迭代域减小;P型迭代学习控制由于存在非重复的时域扰动,因此收敛速度较慢且跟踪精度较低;而非参数化迭代学习算法则对于列车期望轨迹具有较好的跟踪性能,表现为算法具有较快的收敛速度和较高的跟踪精度,当列车运行迭代次数为18次时,距离跟踪误差达到1 m,速度跟踪误差达到0.002 m/s,证明算法能够实现对期望轨迹的精确跟踪。
5 结束语
本文深入分析了高速列车区间运行的动力学模型,为了解决列车运行阻力模型建模困难的问题,提出基于径向基的模糊神经网络算法。根据列车运行高度重复性的特点,并针对现有算法无法学习系统运行的重复性信息的缺陷,将前馈控制的思想引入到现有反馈控制算法中,提出非参数化迭代学习控制算法,并对算法的收敛性进行严格的数学证明。
通过设置相应的仿真条件,对所提出算法的跟踪性能进行仿真验证,结果表明,所提出的算法能够实现对列车运行阻力模型的渐进逼近,通过列车在区间内重复运行,验证了算法具有较快的收敛速度和较高的跟踪精度,在有限的迭代次数内,能够控制列车精确跟踪期望轨迹,证明了算法的有效性。

