数学课堂练习设计的四个关注点
林小平
数学课堂练习,是指教师为了巩固数学课堂教学效果而设计的供学生在课堂上进行的练习。它是数学课堂教学的重要组成部分。不仅是促使学生巩固知识、熟练技能、启发思维、培养能力、发展智力的重要手段,而且是改变教师教的方式,提高教师对数学课程设计与执行能力的重要阵地。设计合理的数学课堂练习,关注并落实好基础性目标和发展性目标,于生于师,都能实现精神的成长、能力的提升、智慧的生长。
一、 练习设计要注意固本强基,使学生举一反三
固本强基是每个数学课堂练习必须完成的任务,起到“筑牢根基”的作用。孔子的“闻一以知十”和荀子的“以近知远,以一知万”,说的就是“举一反三”。举一反三能及时丰富和更新学生原有的认知,使学生对知识的获得更为全面,理解更为深刻。两者若双管齐下,能固本夯基,触类旁通,如太极一般,达到“四两拨千斤”之效。
例如,人教版五年级上册“数学广角”中的植树问题,教师设计了这样的题组练习:
① 同学们在全长20米的小路一边植树,每隔5米栽一棵(两端都栽),一共要栽几棵树?
② 同学们在全长35米的小路一边植树,每隔5米栽一棵(两端都栽),一共要栽几棵树?
③ 同学们在全长35米的小路两边植树,每隔5米栽一棵(两端都栽),一共要栽几棵树?
④ 同学们在全长35米的小路两边植树,每隔5米栽一棵,可能要栽几棵树?
⑤ 议一议,如果要在圆形池塘边植树,会和哪种情况相同?为什么?这个经验还能推广到生活中的哪些现象?
以上题组设计,教师切准了知识之间的联系和变化,紧紧抓住“总长度÷每段长=段数”这个基本数量关系,通过变式练习举一反三,能让学生学会根据实际情况判断“点数”和“段数”的关系。从数学的角度看,世事都是千变万化的,但变化中又蕴涵着变与不变的哲学思想。教师在引导学生思维拾级而上的过程中,注重对比辨析,让学生关注到哪些量在变,哪些量始终不变,变化的量又会引起哪些量的变化,在变与不变的研究中学习数学,感受“万变不离其宗”的思想。这种思想的熏染,有助于学生形成模型意识,培养学生求同又求异的思维品质,提高学生思维的深度、广度和灵活度,加强学生解决复杂问题的能力。
因此,教师设计习题,既要注意夯实基础,又要凸显举一反三,抓好基本点,触发生长点,让知识串成线、连成片、搭成体,更显知识生长的力量。
二、 练习设计要注意新颖有趣,对学生富有挑战性
新颖的课堂练习能吸引学生的注意力,带给学生新奇感,对学生的学习起到定向、持久和强化的作用。如果练习题还带有挑战性,那就更能激发起学生的挑战心,在课堂气氛稍显疲惫的当口,如一支强心针,促使学生不由自主地投入探究,从而减负提质,在发展智力的同时,情感、态度、价值观也得到提升。因此,教师在设计练习题时应在“新、趣、活”上下功夫。
例如,在苏教版四年级下册“三角形的内角和”一课收尾部分,教师设计了这样一道练习题——“三兄弟之争”的故事:在一个直角三角形里住着三个内角(见图1)。平时,它们三兄弟非常团结。可是有一天,老二突然不高兴,发起了脾气。它指着老大说:“你凭什么度数最大?我要和你一样大。”老二想和老大度数一样大可能吗?为什么?如果你是老三,你会怎么对老二说?请同学们用今天学习的知识来解释。
这个习题,教师将理解“三角形中不可能有两个直角或两个钝角”的知识以故事的形式呈现,给原本看起来枯燥严肃的辨析题添上了动漫的色彩。随着卡通小人的娓娓道来,习题变得童趣十足,吸引学生专注地倾听,积极地思辨,学生的大脑会在短时间内迅速调取有用的知识和资源,通过合理的整合与加工,以说理的形式表达出来,说理的过程极具挑战性,对建立学生自信心,锻炼逻辑思维能力、语言组织能力、口头表达能力、质疑辨析能力,综合运用知识解决问题的能力都大有裨益。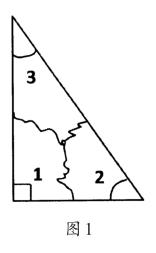
因此,教师设计习题,可将知识的曲折处和教材的潜隐处融进故事、游戏、图像之中,让学生在看似好玩、却带挑战性的活动中完成对知识的理解、消化和巩固。
三、 练习设计要注意实践体验,发展学生思维
意大利教育家蒙台梭利早在19世纪就提出了“实践是最好的老师”的教育思想。她说:“对孩子来说,听到的,容易忘记;看到的,记忆不深;只有亲身实践和体验到的,才会刻骨铭心,终身难忘。”由此可见,实践和体验是学生认识世界的最好方式。数学新课程标准倡导“做中学”,就是以身体的动作来促进思维的发展。因此,教师在设计练习题时还应挖掘可以“做”的元素,让“儿童的智慧在他的手指尖上”跳跃。
例如,苏教版三年级下册“长方形、正方形的周长和面积”的复习课上,教师设计了这样一道习题:
在一张长30厘米,宽20厘米的长方形纸上剪掉一个长20厘米,宽10厘米的小长方形纸,可以怎样剪?剪后原来长方形纸的周长和面积会发生怎样的变化?
① 先想一想,再畫一画示意图,看看有什么发现?
② 还有不同的剪法吗?继续试一试,看看有没有新发现?
③ 在小组里交流你的发现。
小学生年龄尚幼,思维浅显,对上题“面积变化引起周长变化”的普遍认知是“面积变小,周长也一定变小。”但他们又是天生的发现者和创造者,实践体验能帮助他们“回味”“反刍”,进而“自纠”“互启”,发现“面积变小,周长可能变小,也可能相等,还可能变大”,学会根据实验数据和操作结果来理性地分析问题,建构起较为完整的知识体系。这样设计,既让学生学习数学的基本方法,又锻炼了动手能力,思维的批判性、发散性和全面性也得到发展。
因此,教师设计习题,可将知识的易错点、混淆处设计在“动手做”的问题情境中,把知识的形成过程和学生富有情趣与挑战的探究之旅结合起来,真正“教活”“学懂”“弄通透”,使学生的思维品质得到培养,活动经验得到积累,“手、脑、身、心”和谐发展。
四、 练习设计要注意灵活开放,提升学生的学习力
学习力并不单指学习能力,它是学习动力、学习毅力和学习能力的综合表现。灵活开放的习题,是灵活开放课堂的重要组成部分,能促使学生深度学习,让学生的大脑就像四通八达的高速公路,思维就像高速公路上奔驰的汽车,忙而不乱,快而不燥,持续给力,从而快速提升学习力。
例如,教学苏教版四年级下册“三角形的三边关系”时,教师设计了这样一道练习题:
李叔叔想做一个三角形支架,他有一根120厘米长的木条,打算锯成三段用。他可以分别取多长?最长的一根不能超过多少厘米?(答案都取整厘米数)
前期,学生对“如何才能围成一个三角形”在操作层面上已有了正确的认识,对“三角形任意两边之和大于第三边”的本质特征也有了清晰的认识,能根据一条或两条边的长度推断其它边的长度。而这道题提供的是三角形三边的总长,要让学生自主设计三边各自的长度。虽寥寥数语,但情境更为复杂,答案更为开放。开放的答案并不意味着无止境或者杂乱无章,它要求学生在确保三角形成立的基础上,对边的取值范围有规律性的把握,在学以致用中建构起关于三角形三边关系的新范式。这标志着学习的过程从具体走向了综合,对知识的理解从清晰走向了通透,学生的思维走向了更高阶段。
因此,教师设计习题,不仅要彰显知识的本质,还要关注学生的发展。要努力践行陶行知先生的教材观——我们要活的书,不要死的书;要真的书,不要假的书;要动的书,不要静的书;要用的书,不要读的书。如此,数学也就真正走进了学生的心中,它会和积木一样好玩,和魔术一样神奇,和美食一样让人念念不忘……
每个数学教师,既要能“钻”进教材,又要能“跳”出教材,让练习设计多点新发现和新思路,让学生在充满挑战、丰富多彩的练习中,获得新鲜、强劲、持续的数学学习体验,激发内驱力,提升学习力。
(作者单位:无锡市峰影小学)

