巧用补形法研究四面体问题

曾睿

[摘  要] 立体几何问题中，有一类问题可以通过补形法，得到一个常见的几何体，使复杂的线面关系变得清晰明了. 文章从一道例题出发分析解决这类问题的方法，并在此基础上总结规律，归纳常见的一些四面体的补形方法.

[关键词] 立体几何;四面体;补形

教学中，遇到这样一个问题：已知在半径为2的球面上有A，B，C，D 四点，若AB=CD=2，则四面体ABCD的体积最大值为多少？

这是某年数学全国卷的第12题，主要考查几何体的体积的计算、球的性质、异面直线间的距离，通过球这个载体考查学生的空间想象能力和推理计算能力.

解答是这样的：过CD作平面PCD，使AB垂直于平面PCD，交AB于P. 设点P到CD的距离为h，则有V■=■×■×2×h×2=■h，当直径通过AB与CD中点时，h■=2■=2■，故V■=■.

本小题这个解答当中，学生比较疑惑的有两点：（1）为什么可以过CD作平面PCD，使AB垂直于平面PCD，能这样作的前提是AB和CD要垂直，那为什么认定体积最大时AB和CD要垂直？（2）为什么直径通过AB与CD中点时，距离h最大？

要解释清楚这两个疑点，首先需要补充说明一个公式.

四面体体积公式：如果一个四面体的两条相对棱的长分别是a，b，它们的距离为d，所成的角为θ，那么它的体积为V■=■abdsinθ（证明见后）.

根据这个公式，我们首先得到结论：AB和CD必须垂直，即sinθ=90°时才能得到最大的体积.

其次，由于AB=CD=R（球的半径），所以连结球心O和四个顶点，则容易知道△OAB和△OCD都是正三角形.

设AB的中点为E，CD的中点为F，则OE⊥AB，OF⊥CD.

设AB与CD间的距离为d，有d≤EF≤OE+OF. （异面直线间公垂线段最短）

因此，OEF共线时，四面体的体积可以达到最大值，因为OE=OF=■，故V■=■.

？摇？摇这样解决一个选择题比较花费时间，而且在高中数学教学中，不涉及四面体的体积公式，异面直线的距离即公垂线段的长度在教学中也仅仅要求了解.下面我们用补形的思路来解决这个问题.因为题目当中两条线段长度一样，所以考虑把这个四面体补形成一个长方体：

如图1：

则四面体的外接球即是长方体的外接球，四面体的体积是长方体的体积减去四个全等的小三棱锥的体积.

设长方体的边长为a，b，c，体对角线即为外接球的直径，得到：

a2+b2+c2=42，b2+c2=22，所以a=2■，

则V■=V■-4V■=abc-4×■×■abc=■abc=■.

又b2+c2=22 ，所以V■=■≤■（b2+c2）=■，

当且仅当b=c=■时，等号成立.

从等号成立的条件可以比较容易地看出是在AB和CD垂直时，四面体的体积取到了最大值.

我们会发现，使用补形，一下子把陌生的几何体变得熟悉了，原本错综复杂的线面关系也变得清晰起来. 利用这一方法解决某些几何问题，思路清晰明朗，较其他方法简洁明了.

比如刚才提到的四面体的体积公式也可以用补形法得到.

一个四面体的两条相对棱的长分别是a，b，它们的距离为d，所成的角为θ，将四面体补形成平行六面体（因为相对棱的长度不确定，相等的时候才能补成长方体）.

如图2：

那么该平行六面体的底面积为S=■absinθ，平行六面体的体积为V■=■abdsinθ. 同样，该平行六面体由原四面体和四个全等的三棱锥构成. 三棱锥与平行六面体的高相等，底面积为平行六面体的一半，V■=■×■×■absinθ=■absinθ.所以V■=V■-4×V■=■absinθ.

一起来看一下常见的几种四面体补形方式：

一、把四面体的四个面各补上一个三棱锥，最后形成一个平行六面体. 其中正四面体是最特殊的形式，可以补成正方体. 而对棱相等的四面体则可以补形成一个长方体.

例1：正四面体棱长为a，求外接球的半径R.

正四面体补形为一个正方体，正四面体的外接球即为正方体的外接球.

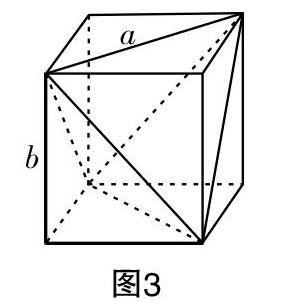
如图3：

正方体的面对角线是正四面体的棱长，体对角线为外接球的直径.

设正方体边长为b，则a=■b，2R=■b，所以R=■a.

例2：在三棱锥A-BCD中，AB=CD=3，AD=BC=4，AC=BD=5，求三棱锥A-BCD外接球的半径.

因为有三组对棱相等，把四面体补成一个长方形，如图4：

长方体的三个面的面对角线是三棱锥的棱长，体对角线是外接球的直径.

设长方体的棱长为a，b，c，外接球的半径为R，

则a2+b2=32，b2+c2=42，a2+c2=52，（2R）2=a2+b2+c2，所以R=■.

二、把四面体的一个角作为平行六面体的一个角补形成平行六面体.

例3：四面体ABCD，侧棱AB，AC，AD两两垂直，AB=2，AC=3，AD=4，求四面体的外接球的半径R.

因为四面体的侧棱两两垂直，所以可以把这个角看作长方体的一个角，把四面体补形成一个长方体，则四面体的外接球就是长方体的外接球

四面体的三条侧棱就是长方体的长、宽、高，外接球的直径就是长方体的体对角线，则（2R）2=AB2+AC2+AD2=29，所以R=■.

例4：若三棱锥S-ABC的所有顶点都在球O的球面上，SA⊥平面ABC，SA=2■，AB=1，AC=2，∠BAC=60°，求球O的半径R.

根据已知条件可以得到△ABC是直角三角形，把四面体补成一个长方体，则四面体的外接球就是长方体的外接球，外接球的直径就是长方体的体对角线.

则（2R）2=SA2+AC2=16，所以R=2.

例5：已知四面体PABC的侧面PAC与平面ABC垂直，∠ABC=90°，BC=2■，AB=2，且PA⊥PC，PA=PC，求异面直线PC与AB所成角的余弦值.

解答：把四面体补成如图所示平行六面体，异面直线PC与AB所成角即为PC与CD所成角的补角的余弦值.

取AC中点M，PA=PC，则PM⊥AC，又因为平面PAC与平面ABC垂直，所以PM⊥平面ABC.

△ABC中，∠ABC=90°，AB=2，BC=2■，所以∠ACB=30°，AC=4.

△PAC中，PA⊥PC，PA=PC，AC=4，所以PM=2，PC=2■.

底面四边形ABDC中，DM2=DC2+CM2-2DC·CM·cos120°，得到DM=2■.Rt△PMD中，PD=4.

△PCD中，cos∠PCD=■= -■.

所以异面直线PC与AB所成角的余弦值为■.

此题也可以用空间向量法解答，用补形能更好地体现线面关系.

三、把四面体补形成三棱柱

例6：已知某几何体底面ABC是棱长为1的等边三角形，PA⊥平面ABC，PA=3，求该几何体的外接球的半径.

解答：将该四面体补形成一个三棱柱

四面體的外接球就是三棱柱的外接球.

先求三棱柱底面三角形外接圆半径r=■·■=■.

又因为PA⊥平面ABC，PA=3，

所以三棱柱的外接球半径为R=■=■.

四面体的问题可以通过补形变成正方体、长方体乃至平行六面体的问题.尤其在正方体和长方体中，点线面的关系是我们所熟悉的. 一些几何题的证明和求解，由原几何图形分析探究会比较烦琐，通过补形填补成一个新的几何图形，能使原问题的本质得到充分的体现，解决起来比较容易. 本文着重讨论四面体的补形问题，希望窥一斑而知全豹，探究立体几何中补形法这一重要的转化策略.