初中数学微专题设计案例举隅

【摘要】微专题设计是一种教与学的新模式。通过对一些知识点做深入的系列化研究，找到学生数学学习的薄弱点和思维的拐点，以“小”见“大”，培养学生的直观感知能力;由“表”及“里”，培养学生的逻辑推理能力“;精”益求“精”，培养学生的综合应用能力。

【关键词】微专题;设计案例;初中数学

【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009（2020）83-0041-04

【作者简介】陈冬，江苏省张家港市妙桥中学（江苏张家港，215615）副校长，高级教师，江苏省特级教师。

初中数学微专题是常规数学教学的一种补充。它强调立足于学生实际和学习要求，对一些问题进行仔细梳理、筛选与提炼，从中遴选出切入口小、针对性强、角度新的微型问题进行突破，以达到相关教学目标。基于这样的特点，笔者以为，微专题中，“微”只是形式，

“专”才是其本质。微专题设计，不宜标新立异，而应有机穿插，以“小”见“大”，旨在对常规教学做补充。为此，微专题的设计应更符合学生实际，例如可以从初中数学教学中“考点”的细化、“知识点”的延伸、“易错易混点”的辨析、

“思维角度”的转换、“边缘知识”的渗透等角度去研究与设计微专题。此外，微专题教学还有利于学生相关能力的培育，笔者从自己的实践出发，现举例如下。

一、培养学生直观感知能力

微专题1：锐角三角函数的应用。

笔者的大体设计如下：

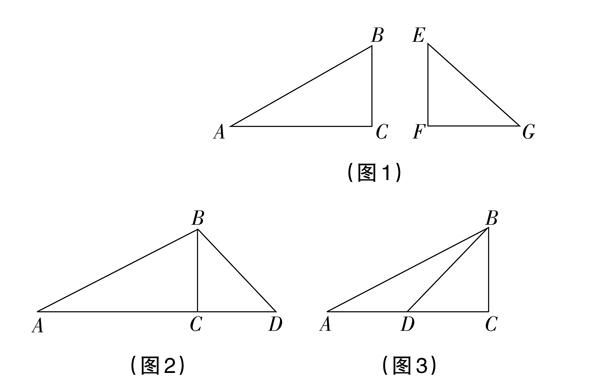
首先，给学生提供如图1所示的两块三角板（其中BC=EF），由学生进行拼接，引出本节课的主题图（图2和图3）;

其次，分别给图2和图3中三角形的角度与边长赋值，让学生求其他边长。例如在图2中，已知∠A=30°，∠BDA=45°，问：若BD=2，则能求出其他的边长吗？若AB=2呢？

最后，给出一道拓展题，供学生研讨。

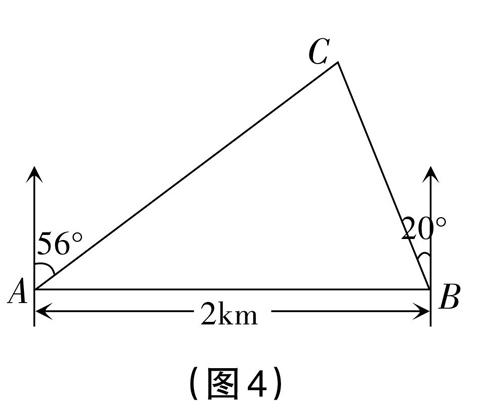
如图4，在一笔直的海岸线上有A、B两个观测站，A在B的正西方向，AB=2km，从A测得船C在北偏东56°的方向，从B测得船C在北偏西20°的方向，求船C确到0.1km）。（sin56°≈0.83，cos56°≈0.56，tan56°≈1.48，sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）

【设计意图】数学教学专家罗增儒教授在《解题学引论》中提出：“学习数学的过程中，所积累的知识经验经过加工，会得出有长久保存价值或基本重要性的典型结构与重要类型——模式，将其有意识地记忆下来，并作有目的的简单编码。当遇到一个新问题时，我们辨认它属于哪一类基本模式，联想起一个已经解决的问题，以此为索引，在记忆贮存中提取出相应的方法来加以解决，这就是模式识别的解题策略。”罗教授这里说的“模式”，笔者的理解就是指数学模型。因此，在平时数学教学中，我们要提醒学生重视数学模型，注意积累和运用数学模型，从而提高解题能力。本案例从学生十分熟悉的两块三角板入手，通过拼接逐渐发展变化形成“主题图”，在“主题图”变化的过程中，不仅发展了学生的直观感知与思维能力，而且让学生思考如何解决此类问题。找到了解决此类问题的关键，总结出了解决此类问题的策略，学生解决此类问题的能力才能得到提升。

二、培养学生逻辑推理能力

微专题设计往往从根源上一挖到底，将某一类问题研究透彻，使学生对这类问题能有一个清晰而透彻的认识，也使学生的学习能由横向上的“细致”走向纵向上的“深入”。由此，微专题设计要由“表”及“里”，着力培養学生的逻辑推理能力。

微专题2：图形的翻折。

笔者的大体设计为：

先带领学生回顾如何找出对称点、利用对称性画出翻折后的图形、翻折后图形的性质等已学知识，再精选例题进行讲解。

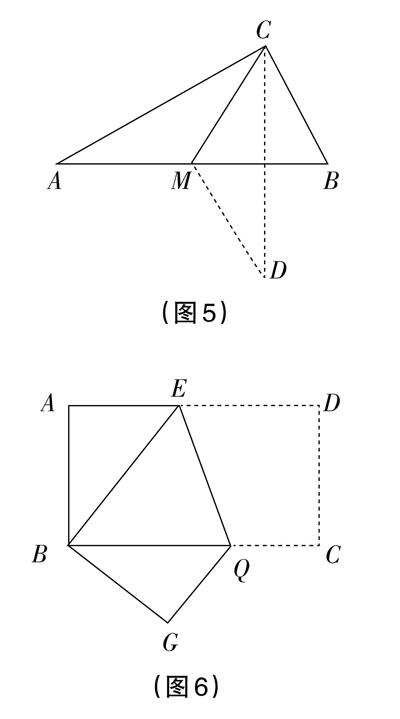
例1：（1）如图5，在Rt△ABC中，∠ACB=0°，∠A<∠B，CM为斜边上的中线，将△ACM沿着直线CM折叠，点A落在点D处，若CD⊥AB，则∠A=_______°。

（2）如图6，长方形纸片ABCD的长为9，宽为3，将其折叠，使点D与点B重合，求折叠后DE的长。

例2：如图7，已知矩形ABCD，将△BCD对角线BD折叠，点C落在点E处，BE交AD于点F。根据图形，先画出翻折后的图形，你能发现图中有哪些因翻折而产生的相等的角和线段？

（1）若∠ADE=40°，则∠EBD=_______°;

（2）若AB=4，BC=8，求AF的长度;

（3）连AE，求证：AE∥BD。

延伸思考：

（4）在（2）的情况下，S△AEF=_______;

（5）延长BA、DE相交于点G，联结GF并延长交BD于点H，求证：GH垂直平分BD。

【设计意图】本案例要求学生能理解图形翻折的直观意义，认识平面图形翻折的过程，在实例中理解轴对称的意义。根据要求能画出依线翻折后的图形，知道翻折后图形的形状、大小保持不变，能运用翻折后的图形的性质解决数学问题，提高学生解综合问题的能力。例1的第（1）小题，先显示翻折图形，问学生这个图是如何作出来的，教师演示作图过程。第（2）小题可以师生互动完成作图，通过动态演示，达到直观效果，也启发学生由翻折后图形的性质作为已知条件解决本题。例2第（1）小题是相关角度的计算，第（2）小题是相关线段的计算，第（3）小题是相关几何证明。这三个小题都围绕“折叠的性质”展开，折叠是一种对称变换，属于轴对称。折叠前后图形形状、大小不变，只是位置变化，对应边、对应角相等。思考题属于提高部分。第（1）题与面积相结合，两个三角形是同高，面积之比等于底之比;第（2）小题需要用到“线段垂直平分线的判定定理”。本案例看似是简单的“图形翻折”，但就“图形翻折”深挖，层层推进，不仅让学生看到了“图形翻折”的很多知识，而且也利用“图形翻折”渐渐地培养了学生逻辑推理能力。

三、培养学生综合应用能力

微专题设计的一个明显特征就是“精”，主要体现在精选例题，让学生就题目的不同特点选择不同的方法，提高选择合适方法解决问题的能力;精准练习，让学生去悟透其包含的数学思想方法，从中获得一定的数学活动经验。因此微专题要设计“精”益求“精”，培养学生的综合应用能力。

微专题3：动态问题中的相似三角形——全等变换与相似三角形。

笔者设计了4个环节6道例题来进行此微专题的教学。

（1）课前导学。

例1：如图8，在△ABCA中，∠ACB=90°，AC=3，BC=4，将△ACD沿AD折叠，使点C落在斜边AB上的点E处。则线段CD的长度为。

例2：如图9，△ABC中，∠ACB=90°，AC=4，BC=3。将直角△ABC绕点C按顺时针方向旋转90°到△A1B1C位置，再将△A1B1C沿射线CB平移到△A2B2C1位置，若点B2恰好落在AB上，则平移的距离是。

（2）典例導悟。

例3：如图10，将△ABC绕着顶点C按顺时针方向旋转得到△A′B′C，旋转角度为α（0<α<180°），连接AA′，BB′，射线BB′交AC于点M，交AA′于点N。求证：AM/BM=MN/MC。

例4：如图11，△ABC为等边三角形，其边长为8，E为AB边上一点，F为AC边上一点，将△AEF沿EF翻折，使A点落在线段CB上的点D处，且BD=2。求线段AE的长。

（3）学以致用。

变式1：如图12，△ABC为等边三角形，其边长为8，E为AB边上一点，F为射线AC上一点，将△AEF沿EF翻折，使A点落在射线CB上的点D处，B且BD=2。求△BDE与△CFD的周长比。

（4）拓展延伸。

变式2：如图13，△ABC为等边三角形，其边长为8，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，使点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点。问：当线段BE为何值时，线段AM最短，最短是多少？

【设计意图】通过“课前导学”的两道例题，师生一起回顾了“平移、旋转、翻折”三种变换;初步感受了动态变换中虽然图形位置发生了改变，但对应线段、对应角没有改变的特征，从而抓住“变中不变”这个特点，通过相似三角形的性质，建立方程模型求解问题。例1和例2让学生经历了“通过相似三角形的性质建构方程模型来解决问题”的过程，例2还出现了“一线三等角”相似模型。变式1是在例2的基础上进行的，让学生充分接触并体会了“多题一解、变中不变”的解题策略。变式2再次出现“一线三等角”相似模型，通过相似三角形的性质建构函数模型解决问题。整堂课虽然题目不多，但是精挑细选，一题多变，题题相连，三种变换一应俱全，让学生经历了“寻相似三角形，证相似三角形，用相似三角形”的过程，充分感受到了相似三角形在解决动态变换问题中发挥的作用，达到“会一道，明一串”的效果。

综上，微专题设计是常规课堂教学的有机穿插和补充，可以弥补传统数学教学的不足和缺陷，从而实现数学教学的优化和创新。借助微专题设计，可以在复习数学基础知识的同时，帮助学生形成良好的认知结构，活化数学知识的运用，真正实现从知识本位的掌握走向关键能力的培养。但微专题设计中选择的难易度、切入的角度、挖掘的深度等方面的把握仍需要我们一线数学教师展开进一步探讨。

【参考文献】

[1]张俊.高三数学微专题复习的实践与思考[J].教学与管理，2020（4）：55-57.

[2]吕增锋.数学“微专题”设计“三要素”[J].数学通讯，2017（12）：50-53.

[3]教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

[4]李宽珍.再谈高中数学“微专题”教学——微专题的编制策略与方法[J].中学教研：数学，2016（6）：5-8.

[5]丁称兴.小小“微专题”蕴藏“大能量”——浅谈高中数学二轮复习中“微专题”的使用[J].中小学数学：高中，2014（4）：49-51.

[6]洪兵.高中数学教师微专题研究的开展[J].教学与管理，2017（34）：57-59.