危险天气下航路网络流可靠性的动态管理
王莉莉,王航臣,赵 迪,李彦吉
(1.中国民航大学天津市空管运行规划与安全技术重点实验室,天津 300300;2.北京交通大学交通运输学院,北京 100044;3.河北省城市客运管理局,石家庄 050000;4.北京铁路局石家庄供电段,石家庄 056002)
航路网络作为空中交通系统运行的载体,其通行能力的高低直接决定了空中交通网络的运行效率[1]。随着中国民航运输的发展,繁忙的空域航路网络面临着严峻的交通流量压力。由于危险天气、军航活动等因素,会造成航路网通行能力大幅下降,从而导致局部空域阻塞,“塞机”和延误大量出现[2],在上述情况下,如何预先调度受影响的交通流使航路网络的延误最小,给实际运行提供一个量化的参考,是亟待解决的问题。
空中交通流量管理(ATFM,air traffic flow management)是缓解空域拥挤,减少延误损失的重要方法,空中交通网络流的动态管理是其重要组成部分,但目前关于这个方向的研究较少。2000年,Bertsimas 等[3]最先将网络流理论应用到ATFM 中,使用动态的、多品种流和整数网络流的方法详细讨论了危险天气下空中交通流的改航问题。Ng 等[4]对危险天气下交通流的分配与调度展开研究,在文献[3]的基础上,将各种机型视为交通流,提出了一种模型求解效率较高的算法,该方法虽然能提升运算效率,但对实际场景过于简化,不能很全面地描述实际的管制运行。Taylor 等[5]从网络角度对航空器的改航进行建模,详细讨论了各种突发事件下的安全改航方案,但缺少危险天气等因素使航空器改航后对整个系统通行能力的影响。孟令航等[6]讨论了强对流这一危险天气下的航空器改航,以改航代价最小为优化目标,以航段连续性和最大穿越风险代价为约束条件,建立动态改航路径规划模型,但缺少交通流角度的航路选择与流量分配的相关研究。王莉莉等[7-9]分别从空中交通流分配的基本模型、终端区的受扰通行能力和多机场区域通行能力3 个方面进行建模,将网络流理论应用于其他空域及其组成部分。以上研究鲜有考虑危险天气的随机性因素。
针对危险天气的随机性,建立了航路可靠性的度量方法,并将航路可靠性转化为航路网络中的权重,从天气随机性、航路容量与管制员负荷3 个方面改进最小费用最大流模型,建立了相应的最优化模型。传统最小费用最大流的算法难以求解天气动态变化带来的航路阻抗变化,故设计了一种考虑天气动态变化的阶段性求解的平衡算法,最终达到航路网络流动态管理及减少延误的目的。
1 问题描述
1.1 航路网络的数学描述
中国民航局规定高度层分配的准则是“东单西双”,故可将航路网络看作平面有向赋权连通图。设有向赋权连通图G=(V,E,Wk,Ck,Rk),其中:V 表示机场节点的集合;E 表示各航路的集合,一条连接i,j∈V 的边记为e(i,j);Wk表示第k 个高度层上航路的费用集合,Wk={},用以帮助管制员决策飞机是否选择该航路;Ck为第k 个高度层上航路e(i,j)最大容量的集合,Ck={};Rk为第k 个高度层上航路e(i,j)的可靠度的集合,Rk={}。
为方便分析计算,将同一航路上k 个不同高度层的航路视为网络图中k 条边,称高度层k 为航路k,如图1 所示。
1.2 航路可靠性度量
危险天气指对航空器飞行安全产生影响的全部气象,主要包括雷暴、低空风切变、大气湍流、大风和视程障碍[10]。天气因素是对民航运输影响最大的因素之一,表现为终端区航空器进离场受到延误和航班取消等影响、空域扇区内航空器为避开危险天气改航,从而导致航路通行能力降低。

图1 不同高度层航路的简化表示Fig.1 Simplified representation of routes at different levels
为了给空中交通网络流提供最可靠的路径,需要考虑航路和机场节点两方面的可靠性。衡量路径可靠性准则主要有两种,链条准则和串联准则[11],在航路网络中有不同的意义:在链条准则下,如果某节点位于几条航路上,且其可靠度在构成这些路径的所有单元中最低,则这些航路具有相同的可靠度,因此以链条准则表示路径可靠度反映不出各航路的差别;在串联准则下,考虑到航路网络中的各构成单元对航路可靠度均有贡献,则以可靠度串联的乘积形式表现出各路径的不同。
综上所述,使用串联准则进行描述,航路的可靠度可定义为

其中:Pa表示由源节点s 到汇节点t 的一条由航路组成的通路;RPa表示通路Pa的可靠度;表示节点i 和j之间航路k 的可靠度。为了便于求解,可将式两边取以e 为底的对数,得
由于0≤RPa≤1,ln≤0,所以取对数后若以-ln作为两节点之间航路e(i,j)的费用,则可将可靠性问题转化为最短路问题,继而可将流量调配问题转化为经典的最小费用最大流问题[12]。
综上,可定义费用

2 模型建立
以传统的最小费用最大流模型为基础,引入天气因素,考虑航路和机场节点的可靠性及实际管制运行条件,建立了危险天气下的最小费用最大流模型。
2.1 目标函数
传统的最小费用最大流模型中,目标函数为
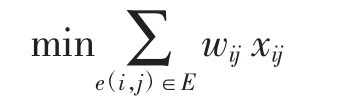
其中,xij表示流量,该目标函数假设费用(阻抗)wij是定值,不随其他因素的变化而变化。而实际过程中许多因素都会使航路的阻抗发生变化,天气便是其中的主要因素之一。
为了衡量天气因素对航路阻抗的影响,对传统的目标函数进行改进,引入可靠度,将可靠度Rij定义为航路e(i,j)不发生危险天气的概率,该参数可由实际观测数据标定。将最小化航路网络阻抗为目标,若以表示航路k 上的流量,则可表示为

2.2 约束条件
1)容量约束
对于每条边e(i,j)运行的交通流量应满足非负性与容量限制条件,即

2)流量守恒约束
在流量分配的过程中,整个航路需要满足流量守恒约束,即对于起止节点s、t,中间点o、d,流入量等于流出量。定义为节点i 和节点j 之间航路k 上运行的交通流量,v(x)为可行流的流量,即源节点的净输出量,则该中间约束可表示为

对于航路的起点s 及网络中与s 相邻的任意一点i,即

对于航路的终点t 及网络中与t 相邻的任意一点j,即

对于航路网络中的某条通路e(i,j),令qij表示出发地i 和目的地j 之间的起止点的交通量,即

3)管制员负荷约束
以Lm表示扇区m 管制员所能指挥的飞机最大流量,空中交通服务计划手册中介绍的“DORATASK”方法[13]指出:管制员的工作负荷必须小于峰值的80%,则该约束可表示为

3 算法设计
解决最小费用最大流的传统算法均是静态算法,难以描述航路网络上天气的动态变化带来的影响。在道路交通领域,求解交通流分配问题已取得了一定的成果,其中,迭代加权法(MSA, method of successive average)通过迭代均衡各路径上的流量,符合实际运行中空域各扇区和各航路流量分布均衡的要求。
求解模型要处理好天气的变化,从而根据实时的天气信息判断各航路的可靠性,并引入天气阻抗。设定每隔1 h 更新一次气象信息。算法步骤如下:
步骤3 按照步骤2 中的气象信息更新航路阻抗,再进行一次0-1 交通分配,得到一组附加流量;
步骤4 用MSA 方法计算各通路当前各航路的交通量

步骤5 收敛性检验,若满足预先给定的误差限值ε,即

4 算例分析
4.1 说明型算例
构造一个只有两条路径(同时也是通路)连接一对起点和终点的简单空中交通网络,如图2 所示。

图2 双路径单OD 对的简单路网图Fig.2 Simple network with two paths and single pair of OD
设容量和管制员承受能力足够大,连续两个时间窗内航路1 发生危险天气的概率为0.35 和0.33,航路2 发生危险天气的概率为0.28 和0.47。某一时间窗内需要通过qst=200 架飞机。
步骤1 航路1 和航路2 均为完整通路,由于发生危险天气的概率为0.35 和0.28,因此Rp1=1-0.35=0.65,Rp2=1-0.28=0.72,根据式(2),可得

步骤2 得到更新后的危险天气概率0.33 和0.47。
步骤3 再次计算航路阻抗,可得

步骤4 取λ=0.5,使用MSA 方法计算,可得
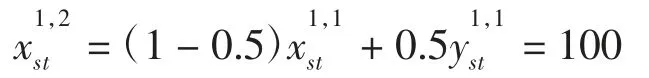
步骤5 令误差限制ε=0.05,经检验,迭代结束。如需分析后续的流量分配情况,可读入新数据。
4.2 应用型算例
在中国民用航空局公布的航行资料汇编(AIP)中截取华北管制区的部分空域,黑色线段为简化后的航路图,如图3 所示。其中:节点1(北京ZBAA)、节点2(天津ZBTJ)、节点3(济南ZSJN)为起飞机场;节点8(呼和浩特ZBHH)、节点9(太原ZBYN)、节点10(石家庄ZBSJ)为目标机场;节点4~7 表示导航台点;节点间的连线表示当地的主要航路,即仿真航路。由于是一个多起点的问题,故可添加虚拟节点使之转化为一个单起止点的问题,并设连接虚拟节点的虚拟航路的容量为M(任意无穷大数)。

图3 仿真空域Fig.3 Airspace simulation
为了便于模型的求解,假设3 个起飞机场节点的起飞流量已知,表1 为ZBAA、ZBTJ 和ZSJN 的离场流量。为了模拟气象条件的动态变化,使用计算机生成随时间变化的气象信息,∀(i,j)∈V,0≤≤1,且其在同一时间窗内不发生变化,在实际的运行可根据该地区历史天气数据进行标定;航路容量=25 和管制员负荷Lm=25 已知且为定值;误差限值ε=0.05。
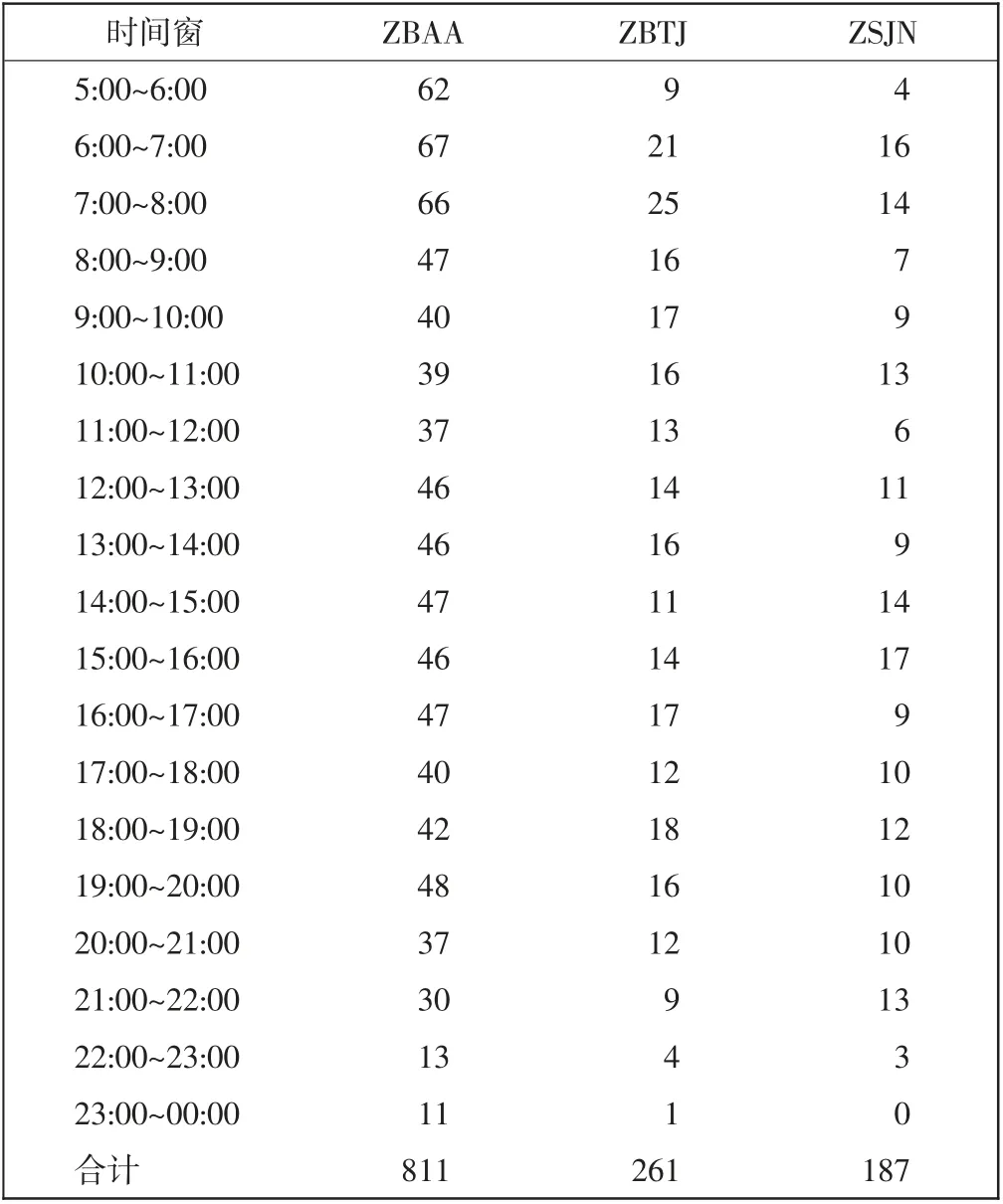
表1 离场交通流量Tab.1 Departure aircraft volume
对算例进行仿真,可以求得分配了ZBAA、ZBTJ和ZSJN 这3 个机场的起飞流量后,3 个机场的平均每架次航空器的离场延误,仿真结果如图4~图6 所示。
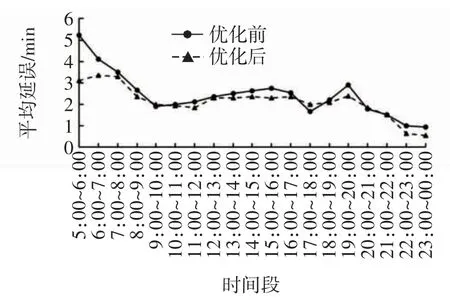
图4 ZBAA 离场延误优化Fig.4 ZBAA departure delay optimization

图5 ZBTJ 离场延误优化Fig.5 ZBTJ departure delay optimization

图6 ZSJN 离场延误优化Fig.6 ZSJN departure delay optimization
由ZBAA 机场的仿真结果可知,离场航空器的延误平均降低12.44%,对于首都机场这种空中交通流量大的机场具有良好的优化效果;由ZBTJ 机场的仿真结果可知,离场航空器的延误平均降低11.98%,对于天津机场这种空中交通流量中等的机场也具有一定的优化效果;由ZSJN 机场的仿真结果可知,离场航空器的延误平均降低6.52%,优化效果一般,可解释为空中交通流量小的机场本身也只存在较小延误或不存在延误。
通过Matlab 2014a 软件使用设计的模型与算法求解模型,算法运行环境为1 台CPU 为Intel Core i5-4590 3.30 GHz×2,内存4 GB 的台式计算机。在算例给出的空域结构下进行仿真,短期ATFM 时间敏感度高,要求在短时间内得到可靠解。ZBAA 流量分配的运算时间为15.79 min,ZBTJ 的运算时间为3.23 min,ZSJN 的运算时间为1.04 min,均能够满足短期ATFM的要求。
5 结语
航路网络流的动态管理是ATFM 的重要组成部分,通过改进最小费用最大流模型,提出了一种考虑天气动态变化、航路容量约束与管制负荷约束的数学模型。针对传统求解最小费用最大流的算法不能适用于阻抗随天气动态变化,提出了一种阶段性求解的平衡算法。以华北管制区的部分空域为算例,结果表明,模型和算法能有效降低延误,对空中交通流量大的机场的优化效果比流量小的机场更明显。

