基于改进介质微扰法的水膜厚度测量理论研究

张淑娥，张天浩，曹宏沛

(华北电力大学电气与电子工程学院，保定 071003)

常规电站中大型冷凝式蒸汽透平的末几级和核电站中透平的全部级都工作在湿蒸汽区，蒸汽湿度会影响汽轮机运行的安全性和经济性[1-3].在湿蒸汽长期测量过程中，腔体内壁表面会沉积一层水膜，水膜会给湿度测量带来测量误差[4]，所以蒸汽湿度传感器内壁水膜厚度的准确测量对提高湿度测量精度具有重要意义.在进行水膜厚度测量时，可以把圆柱腔内壁附着的水膜等效成一层体积为VΔ厚度为b的电介质，此时利用微波微扰法[5-6]可以通过测量谐振频率间接确定环绕电介质的厚度.由于圆柱腔内壁附着水膜属于小体积VΔ而εΔ、μΔ较大的介质微扰情况，在利用介质微扰法推导圆柱腔内水膜厚度和谐振频偏的关系式时，通常采用准静态法[7]近似.考虑到圆柱谐振腔内的电场为交变场，将交变电场下电介质内的电场等效成静电场下电介质内的电场存在误差，影响水膜厚度测量的准确度，所以有必要推导出交变电场下电介质内的电场方程.国内外对交变电场下电介质的研究主要集中于对电介质介电特性的研究[1-4]、电介质极化的微观机制研究[5-6]、光电信号在电介质内的传播特性[7-8]等方面，缺少对交变电场下电介质内电场表达式的求解.因此，本文对交变电场下电介质内电场方程进行了推导，并利用推得的电场方程对谐振腔介质微扰公式进行了改进，最后基于改进的介质微扰公式建立起了圆柱腔内壁水膜厚度和谐振频偏之间的关系模型，对圆柱腔内壁水膜厚度的测量问题提供了解决办法.

1 介质微扰公式的改进

当谐振腔填充的介质有微小变化时，谐振频率将发生微小的变化.谐振腔的介质微扰分为两种情况：腔体不变εΔ、μΔ小的情况；小体积VΔ内εΔ、μΔ大的情况.

当谐振腔体积不变，腔体内填充的介质变成εε+Δ、μμ+Δ.若εΔ、μΔ很小时，可以近似地以E0、H0代替E、H；若小体积ΔV内Δε、Δμ较大则要用准静态法近似.

1.1 准静态法近似

当谐振腔内引入一小介质试样(εΔ、μΔ较大)时，谐振腔受到微小扰动，谐振频率将发生微小的变化[7]，且有

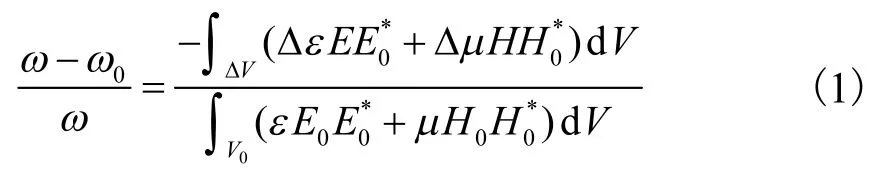
式中：V0为微扰前腔的体积；ε、μ分别为微扰前腔体内的介电常数、磁导率；E0、H0、ω0分别为微扰前腔体内的电场、磁场、谐振角频率；VΔ为介质试样的体积；μΔ、εΔ分别为介电常数变化量、磁导率变化量；E、H、ω分别为微扰后腔体内的电场、磁场和谐振角频率.

准静态法是把原来谐振腔在VΔ内的场E0、H0作为加于介质试样上的外加均匀静态场来处理.图 1为小介质试样(0μΔ=)置于任意方向电场下介质内电场示意.

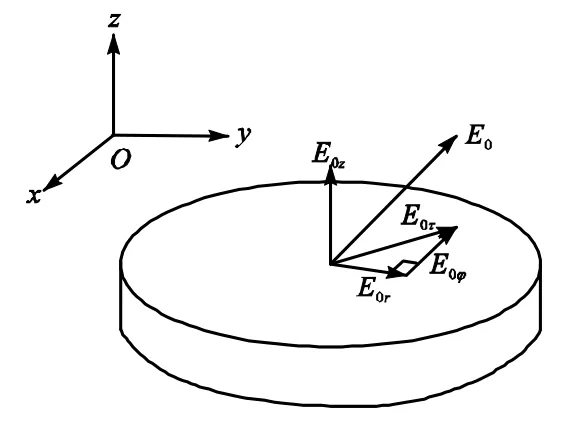
图1 小介质介质内电场示意Fig.1 Small medium sample placed in an electric field

图 1中E0是介质试样所在处的原有谐振腔中的电场.如图1所示电介质试样为一薄圆板，相对介电常数为εr，E0z为E0的纵向分量，与薄圆板相垂直，由于电场的垂直分量必须是连续的，故介质内纵向电场

E0τ为E0在τ平面的分量，与薄圆板相切，由于E的水平分量必须是连续的，故介质内水平方向电场

因此，对置于任意方向交变电场下的电介质来说，电场方向与边界垂直的分量用式(2)近似，与边界相切的分量，则用式(3)近似.故该电介质试样置于任意方向的电场下，采用准静态法近似的介质微扰公式为

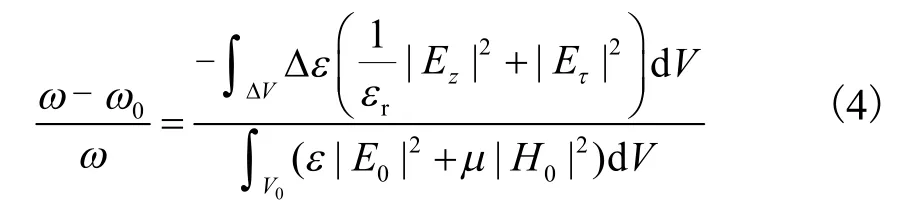
由于谐振腔内的电场是交变场，用准静态法近似始终存在误差，若对测量结果精度要求较高，用准静态法近似的误差就会很明显.此时，就有必要得到交变电场下电介质内的电场表达式.本文首先推导了交变电场下电介质内的电场方程，并应用电介质内电场方程对介质微扰公式进行了改进.

1.2 交变电场下电介质内的电场方程

在外施电场作用下，电介质发生极化，电介质内部产生偶极矩，电介质表面形成束缚电荷[9].这些束缚电荷和自由电荷一样，在电介质内部空间产生附加电场，空间内任意一点的电场是外施电场和束缚电荷产生电场的向量和.

交变电场下，极化强度P(t)随时间变化的方程[10]为

式中：εr、ε∞分别为电介质的相对介电常数和相对光频介电常数；τ为弛豫时间常数.

根据偶极子在点场内的旋转转矩和摩擦转矩相平衡的条件，可推得液体电介质的弛豫时间常数[11]为

式中：a为极性分子半径；η为电介质的黏度，只与温度有关；ξ为旋转内摩擦系数；K为玻耳兹曼常数；T为热力学温度.弛豫时间常数τ取决于电介质本身的特性，是温度的函数，随温度升高，τ按指数式急剧减少，反之则急剧增加.

交变电场下电介质中的合场强E(t)等于外施电场E0(t)与束缚电荷产生电场的向量和，即

这里，将式(5)代入式(7)中，得到交变电场下电介质内的合场强E(t)随时间变化的方程

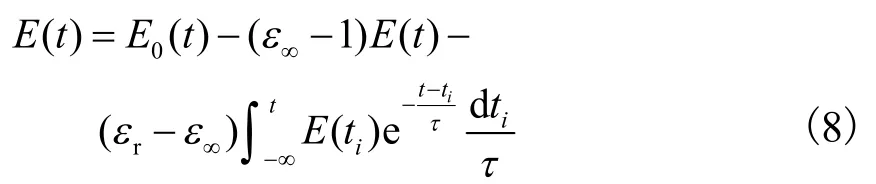
将式(8)两边对时间t求导，整理得到 1阶线性微分方程

对式(9)求解，得到该1阶线性微分方程的解

式(10)即为交变电场作用下电介质内的电场.对式(10)整理得到

其中，

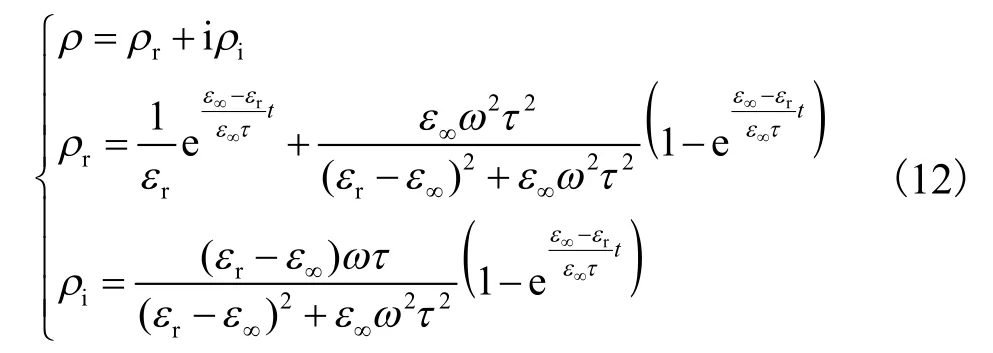
式中：E0(t)为微扰前的电场；E(t)为微扰后介质内电场.微扰前后电场比值ρ与介质的介电常数εr、光频介电常数ε∞、介质弛豫时间常数τ以及频率ω有关.在一定温度下，当介质确定时，ρ只与频率ω有关.

若施加正弦电场E0(t)= sin(ωt)，则微扰前后水内的电场如图 2所示.其中，图 2(a)为原施加正弦电场，图 2(b)为校正后水内的电场.观察可发现，原施电场与校正后的电场相比幅度降低，相角滞后0.1701rad.

因此，式(11)适用于求解任意交变电场下电介质内电场问题.

图2 施加正弦电场微扰前后电场变化曲线Fig.2 Electric field curves before and after sinusoidal electric field perturbation

1.3 介质微扰公式的改进

得到了交变电场下电介质内电场方程后，式(2)应为

将式(13)代入式(4)中，得到

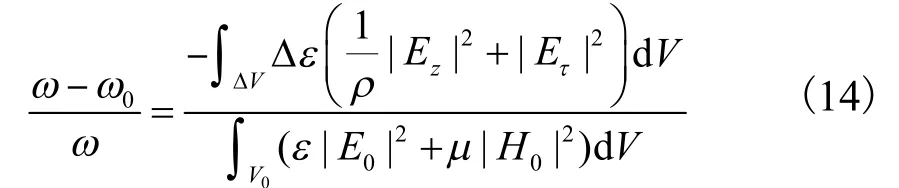
对于有耗的介质微扰，介电常数和谐振角频率均要用复数形式代入，即

将式(15)代入式(14)并整理得到

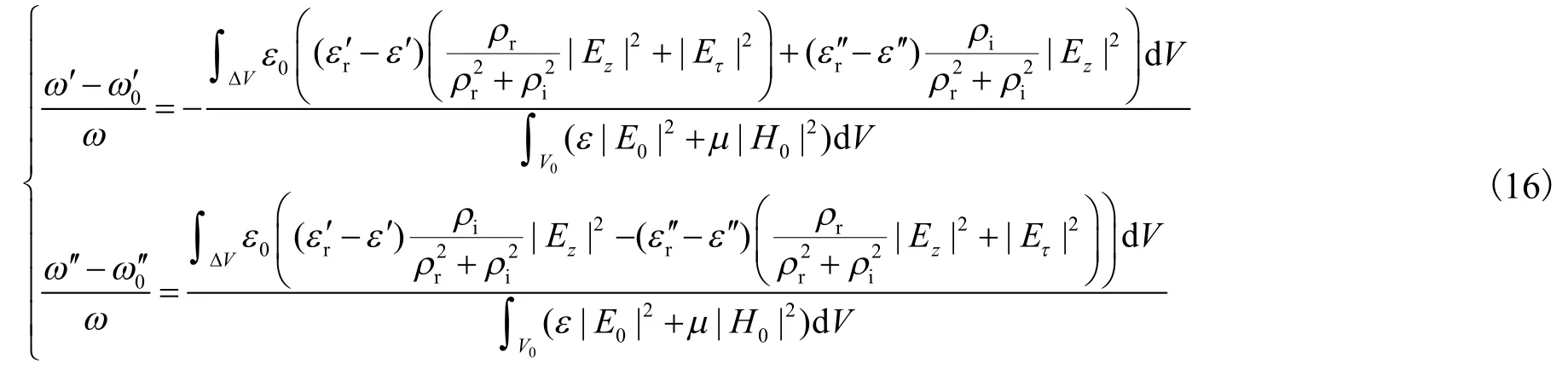
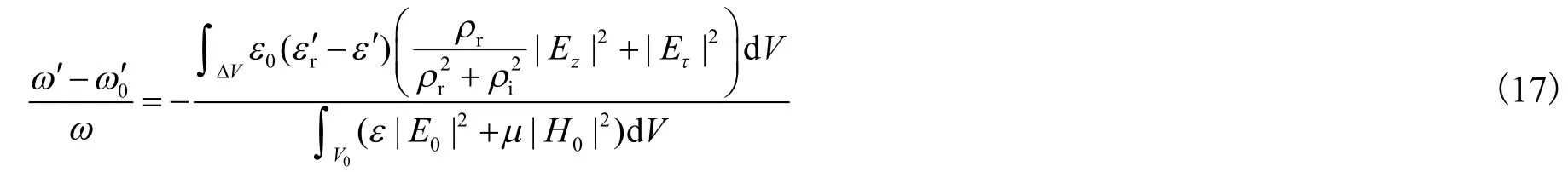
2 仿真验证交变电场下电介质内电场

为了对交变电场下电介质内的电场公式进行验证，利用 HFSS电场仿真软件设计了同轴腔和圆柱腔，在介质一定的情况下，通过改变同轴腔长度分析谐振频率对ρ的影响；在谐振频率一定情况下，通过改变圆柱腔内壁电介质材料分析不同电介质对ρ的影响.

2.1 同轴腔验证

微波谐振腔选用同轴谐振腔，采用 TEM 模式作为工作的模式，在这种工作模式下，谐振腔的结构简单、稳定、无色散、无频率下限[12].采用λ/2型同轴谐振腔，作为谐振频率对交变电场影响的传感器.同轴腔可以看作是由两端短路的同轴线构成的.为了让同轴线只工作在TEM波，同轴腔波长λ满足

式中：D为外导体直径；d为内导体直径；c为真空中光的传播速率；l′为同轴腔长度；f0为同轴腔谐振频率.在同轴腔中，外层介质均匀分布在同轴腔内壁上，且介质厚度为b，内层介质为空气且半径为a1.

对于工作在TEM模式的同轴线，其电场只有Er分量.因此同轴线微扰前后电场变化可以用Er分量上的电场表示.当同轴腔内的介质都为空气时，等间距取电场Er分量上半径为b上的电场，分别为.当同轴腔内壁附着一层厚度为b的液膜后，取相同位置上的电场分别为可以得到微扰前后同一点的电场比值为.

根据式(10)可知，在交变电场下，介质内的电场与腔体的谐振频率有关.因此改变同轴腔的谐振频率即可得到不同频率下介质内电场的变化，如图 3所示.

图3 微扰前后电场比值随谐振频率变化关系Fig.3 Relation of electric field ratio with resonance frequency before and after perturbation

其中同轴腔内填充的液体介质为水，根据图3可知：当谐振频率从1GHz增加到10GHz，由式(11)得到微扰前后电场比值ρ和仿真微扰前后电场比值ρ′都降低，且变化趋势一致.在同一谐振频率下，微扰前后的比值较为一致，且最大比值差为 2.50，最小比值差仅为 1.04.因此可以验证，在同轴腔中，交变电场下介质内电场相较于静电场会减小.

2.2 圆柱腔验证

在 TE111工作模式下的圆柱形谐振腔，具有径向电场分量，且模式最低，使液膜厚度与谐振频率具有较强的相关性，可以较为准确地测量液膜厚度[13].由于在空气和液膜边界处，电场在Eφ分量连续，而Er分量不连续，因此在交变电场下，令φ=0，取电场的垂直分量Er.在同一谐振频率下，取不同的介质，得到微扰前后电场比值ρ′和ρ.

由表 1可知，与静电场相比，在交变电场下，微扰前后电场比值ρ′和ρ都增大，即介质内的电场会相对降低.不同介质下，微扰前后电场实际比值ρ′与式(11)得到的比值ρ是较为一致的.因此可以证明在交变电场下电介质内的电场方程的正确性.

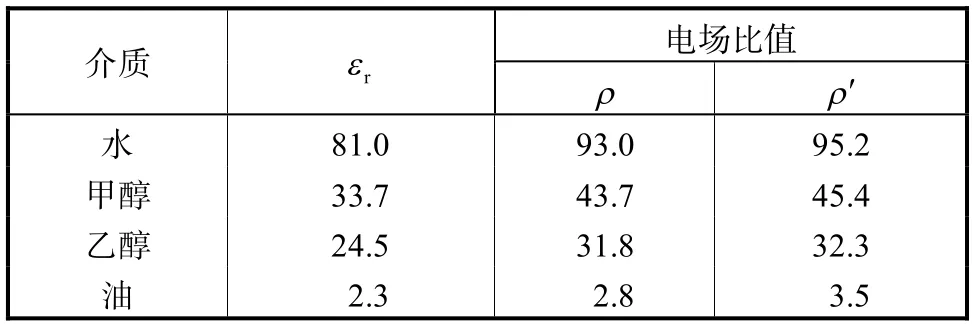
表1 交变电场下微扰前后电介质内电场比值Tab.1 Ratio of the electric field in the dielectric before and after perturbation under alternating electric field

2.3 介质微扰公式验证

当介质厚度一定时，取不同介质微扰后的电场，将交变电场下电介质内的电场方程代入到式(14)中，可得到微扰后谐振腔的谐振频率.

表 2中，f′为式(4)得到的改进前理论谐振频率，f1′为式(17)改进后理论上谐振频率，f2′为实际仿真谐振频率.根据表 2可知：当介质厚度一定时，微扰公式改进前的谐振频率与实际仿真频率相差较大，以介质为水为例，且随着谐振频率的增大，f′与f2′之间的频差逐渐增大，当谐振频率为 5.6166GHz时，f′与f2′之间的频差达到了 37.7MHz，而微扰公式改进后的谐振频率f1′与f2′频差明显缩小至28.0MHz.改变不同介质，f1′与f2′之间的频差都有较大程度的减小.因此改进后的微扰公式可以较为准确反映微扰后的谐振频率，可以说明改进后微扰公式的合理性.

表2 不同介质微扰后谐振频率Tab.2 Resonant frequency after perturbation of different media

3 基于改进介质微扰法的水膜厚度测量理论

自从2003年提出了采用微波谐振腔微扰法进行蒸汽湿度测量[1-3]的方法以来，微波谐振腔测量蒸汽湿度的技术得到了广泛的研究.该方法采用圆柱谐振腔作为湿度传感器，让其工作在 TE011模式下，通过检测频偏来进行湿度测量.

在湿度测量的过程中，由于圆柱谐振腔长期放置于湿蒸汽环境中，腔体内壁会环绕一层水膜.水膜会给湿度测量带来测量误差.若能准确测量水膜厚度，就可通过理论分析扣除误差，所以蒸汽湿度传感器内壁水膜厚度的准确测量对提高湿度测量精度具有重要意义.本节基于改进的微波微扰法，采用圆柱腔TE111模式对腔体内壁水膜厚度进行测量.

TE111模式下，电场只存在水平分量.圆柱谐振腔内电场穿过水膜内任意一点P时的电场分量如图4所示.Eφ、Er分别为腔内轴向、径向的电场分量.

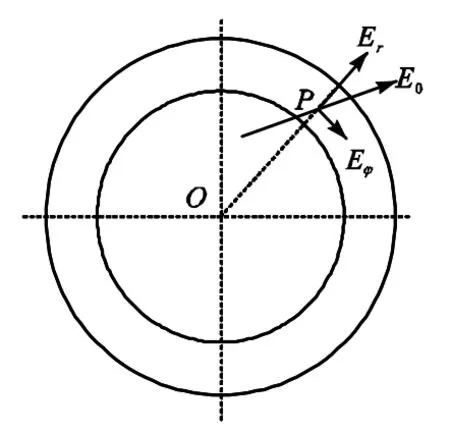
图4 水膜内任意一点电场Fig.4 Electric field at any point in the water film

在测量水膜厚度时不考虑介质损耗，此时，Er与边界相垂直，采用式(13)近似；Eφ与边界相切，采用式(3)近似.故谐振频偏与水膜厚度之间的关系式为

式中：f1、f2分别为微扰(产生水膜)前、后的测量腔的谐振频率；谐振频偏 Δfw=f1-f2.

正常情况下，汽轮机排汽的质量湿度一般不超过15%[13].为了简化分析，假设微扰前圆柱腔内的干饱和蒸汽的相对介电常数，谐振频率是f2[5]，且

式中r、l分别代表圆柱腔的腔体内半径、高度.参考腔的谐振频率只与腔体内半径和腔体高度有关系，因此当腔体结构一定时，参考腔谐振频率就会确定.

TE111模式下圆柱谐振腔的电磁场方程(圆柱坐标系)[5]为

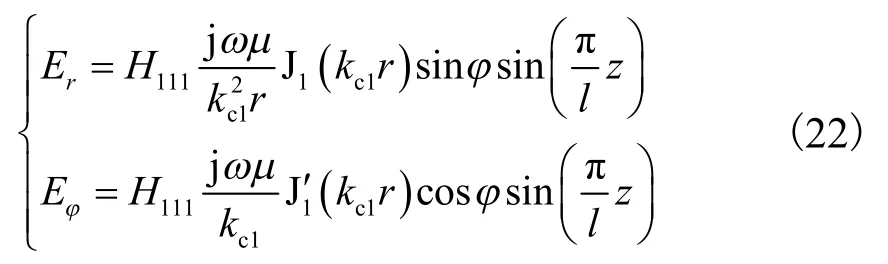
式中：kc1= 1.841/R；R为谐振腔的内半径；r为半径方向变量；z为长度方向变量；J1、J1′分别为1阶贝塞尔函数(Bessel function)、1阶贝塞尔函数的1阶导数.

根据贝塞尔函数[14]递推公式可知

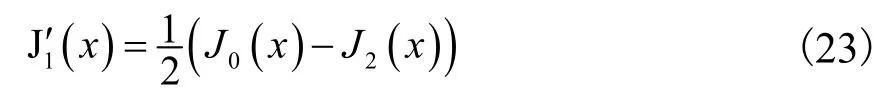
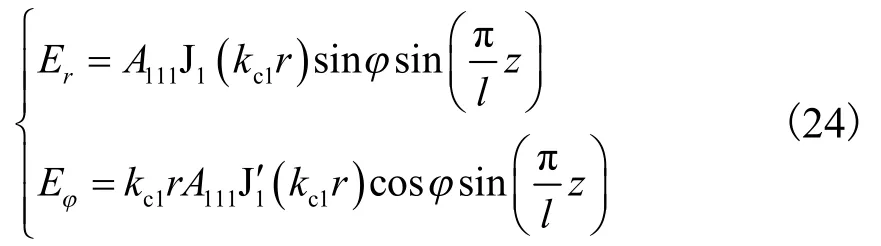
式中A111为腔内磁场强度的幅值.

将式(24)代入公(20)中，得到谐振频偏与水膜厚度的关系为

式中 J0、J1、J2分别为 0阶贝塞尔函数(Bessel function)、1阶贝塞尔函数和2阶贝塞尔函数.

采用 HFSS仿真分析了圆柱谐振腔内壁沉积不同厚度的水膜，水膜厚度变化范围为 10～30μm，间隔是 4μm，在 TE111模式工作时产生的谐振频率，如图5所示.

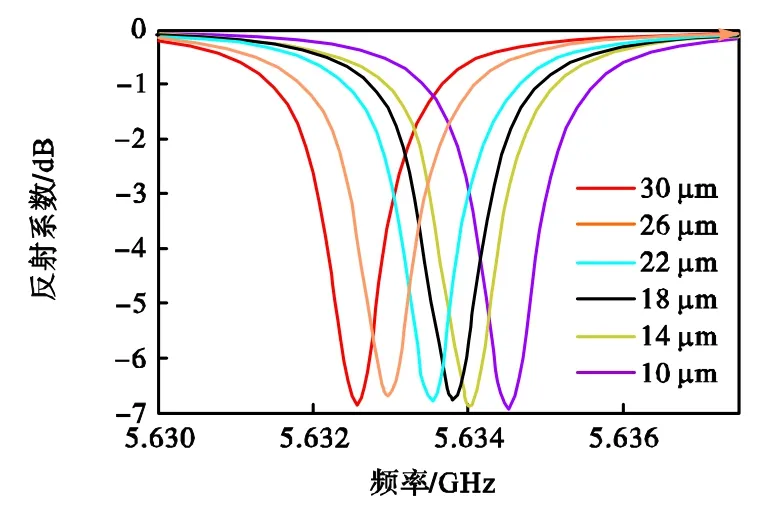
图5 TE111模式下不同厚度水膜的S参数曲线Fig.5S-parameter curve of the water film with different thicknesses in the TE111mode

根据式(23)可以计算出水膜厚度从 10μm 变化到 30μm时谐振频率的理论值.对仿真数据、改进前后理论数据进行处理，得到改进前后理论数据对比图，如图 6所示，在同一水膜厚度下，使用改进后微扰公式得到谐振频率较实际仿真数据更加吻合.当水膜为10μm时，改进前谐振频率的理论与仿真数据相差 0.6MHz，改进后谐振频率的理论与仿真数据相差 0.001MHz，改进后的结果提高了将近 99.94%；当水膜为30μm时，改进前谐振频率的理论与仿真数据相差 4.2MHz，改进后谐振频率的理论与仿真数据相差2.7MHz，改进后的结果提高了35.7%.

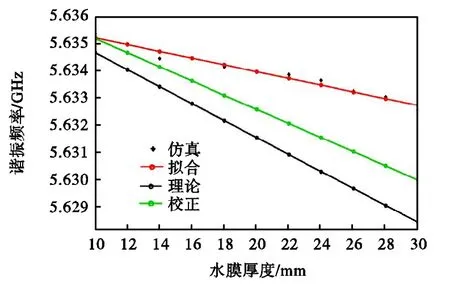
图6 校正前后理论与仿真数据对比Fig.6 Comparison of the theoretical and simulation data before and after correction

4 结 论

(1)推导了交变电场作用下电介质内的电场方程.通过对比原施加正弦电场和校正后电介质内电场，表明了本文推导的交变电场下电介质内的电场方程的正确性，且对任意交变电场都适用.

(2)基于交变电场作用下电介质内的电场方程，得到了改进后的介质微扰公式.

(3)分别用同轴腔和圆柱腔对交变电场电介质方程进行了验证.结果表明：对于不同电介质，仿真和理论得到的电场比值相差不大，且在 1～10GHz范围内，电场比值变化趋势一致，证明了交变电场下电介质内电场方程的正确性.

(4)基于改进的介质微扰公式，建立了圆柱腔内壁水膜厚度和谐振频偏之间的关系模型.结果表明：改进后的介质微扰公式能降低谐振频率偏移，谐振频率的理论与仿真误差至少提高了35.7%.