基于胶结破损机理的非饱和结构性黄土本构模型

蒋明镜 ，卢国文 ，李 涛

(1.天津大学建筑工程学院，天津 300072；2.水利工程仿真与安全国家重点实验室(天津大学)，天津300072；3.同济大学土木工程防灾国家重点实验室，上海 200092；4.同济大学土木工程学院，上海 200092)

在经典土力学中，土体本构模型能很好地反映土体的力学性质，并能将土体的强度问题和变形问题融合，以剑桥模型为代表的弹塑性模型的发展标志着人们认识土体特性的一次飞跃.但这一时期多数本构模型都是针对饱和重塑土发展起来的，在实际工程中遇到的原状土大都具有结构性[1].其不仅与受力历史和土体密度有关，还取决于土粒间胶结物的力学特性.

在过去几十年中，研究人员利用多种方法对结构性黄土进行了数学建模，早期发展的是微观机制模型，其中应用较多的一种为微结构模型，其实质是对土体颗粒及孔隙的排列、形状、接触关系的类型划分和数学建模.Rowe[2]认为宏观塑性应变是在滑移面上所产生的滑移的累加，并在此基础上建立了微观力学模型.沈珠江等[3]率先把损伤理论引入到土体的本构模型研究中，认为天然土的结构破损是从原状土逐渐向扰动土(损伤土)变化的过程.随后建立了弹塑性损伤模型[4]、非线性损伤模型[5]、堆砌体模型[6]，并在此建模思路上开始向岩土破损力学[7]过渡，建立并完善了二元介质类模型.在结构性黄土研究方面，沈珠江[8]较早提出了一个可以适用于黄土的损伤力学模型.Desai[9]于1974年提出扰动状态概念(disturbed state concept)，此后 Desai 等[10]、吴刚[11]在扰动状态概念的基础上建立一系列描述岩土材料力学特性的本构模型，统称为扰动状态模型.与上述建模思路不同，许多研究人员提出表达土体结构性强弱的宏观定量化参数来建立能够描述土体变形和强度规律的数学模型.近年来许多研究人员在临界状态土力学基础上建立适用于结构性土的本构模型[12-13]，称之为临界状态模型.在黄土本构模型研究方面，陈正汉等[14]将该关系式引入到弹塑性模型中，给出了湿陷变形的计算方法，得到了湿陷初始面，但模型参数确定需要进行较多的试验，且只能计算增湿到饱和状态的变形.Jiang等[15]基于沈珠江提出的广义吸力的概念提出了可描述结构性黏土的逐渐破损过程的结构性黏土的结构吸力模型.谢定义等[16]提出了结构性定量化指标——综合结构势.

鉴于传统方法建立的本构模型中的一些关键变量缺乏微细观力学机制的支撑，基于宏微观土力学的研究思路[17]，蒋明镜等[18]通过二维离散元法验证了胶结破损规律，并建立了天然结构性土的本构模型.张伏光等[19]通过三维离散元法建立了胶结砂土的本构模型.笔者认为，结构性黄土的研究需要同时考虑黄土的非饱和性.然而非饱和土本构模型非常复杂，基质吸力对土体抗剪强度的影响呈非线性，另外，基质吸力对非饱和土压缩性的影响以及土水特性曲线的引入都加大了建模难度.为了简化建模过程，李广信等[20]曾对非饱和土的实用化模型展开过探索和研究.

为此，本文以岩土破损力学及临界状态土力学为框架，基于实用化宏微观土力学研究思路，通过建立非饱和吸应力与饱和度的关系式，将临界状态线、扩展椭圆屈服面和临界 Lade-Duncan强度准则推广到非饱和土体，采用三维离散元模拟分析表征结构性损伤的胶结破损规律及其参数建议公式，然后将其引入到硬化规律中，建立了基于经典弹塑性模型的非饱和黄土三维本构模型，并通过黄土室内试验进行了验证.

1 本构模型

1.1 有效应力原理

对于饱和土，太沙基提出了有效应力的概念并在此基础上建立了古典土力学.对于非饱和土，有效应力(沈珠江[21]称为广义有效应力)为

为了模型的实用性，本文仅引入饱和度，不引入吸力和土水特性曲线，用饱和度计算吸应力ps.本文对不同含水量结构性黄土离散元试样进行了离散元模拟分析，采用幂函数描述吸应力和初始饱和度的关系以反映初始饱和度对吸应力的影响，如式(2)所示.

式中：ξ表示土体非饱和程度；cw和nw为拟合参数；Sr为土体的饱和度.

如果考虑某些试验中饱和重塑土也存在黏聚力(如式(3)所示)，可以将吸应力计算式延伸为

式中ps0为饱和土的吸应力，根据饱和重塑土或结构性土临界状态强度线求取.

1.2 临界状态强度面

图 1给出了结构性黄土离散元试样真三轴试验π平面强度(数据点)与 Lade-Duncan准则对比[22](曲线)，该模拟在软件 PFC中实现，主要步骤为离散元试样制备、预压、真三轴试验模拟.在使用 Lade-Duncan准则时，临界状态应力比Mcr取相应饱和度常规三轴试验结果，峰值强度为Mf=qf/p，qf为相应饱和度常规三轴试验峰值强度包面上与p′相对应的纵坐标(偏应力)值.从图 1中可以看出，在使用有效应力的前提下，Lade-Duncan准则能够较好反映非饱和结构性黄土离散元试样的π平面强度.因此，采用有效应力概念后，Lade-Duncan准则可以非常方便地将应用范围从无黏性土扩展到有黏聚力的非饱和土体.

鉴于此，本文在建立非饱和结构性黄土本构模型时采用Lade-Duncan准则作为临界状态强度.其强度包面可表示为

式中：θσ为应力罗德角；M(θσ)为随θσ变化的土体强度线斜率.从图中也可以看出，Lade-Duncan考虑了中主应力与罗德角的影响，不同主应力系数b或罗德角θσ条件下的M(θσ)可由中主应力系数为0(三轴压缩条件下θσ＝-π/6)时的强度线斜率Mcr求得，具体计算方法见文献[23].

1.3 屈服函数

椭圆屈服面在应用于结构性土体时，屈服面“干侧”不能很好地描述室内试验情况[24].依沈珠江[25]关于破坏准则和屈服函数的总结，采用封闭型函数拓展椭圆屈服面，即

式中：ns为形状参数；η′为有效应力比；为结构性土屈服面在p轴上的截距.

将式(6)变形可得式(7)，即

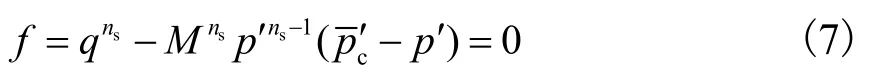
图 2给出了不同ns的扩展椭圆屈服面形状，从图中可以看出，当ns＝2时，式(7)退化为修正剑桥模型的椭圆屈服面；当ns＜2时，屈服面峰值左移；当ns＞2时，屈服面峰值右移.一般说来，对于重塑和结构性土体，应取ns＞2.

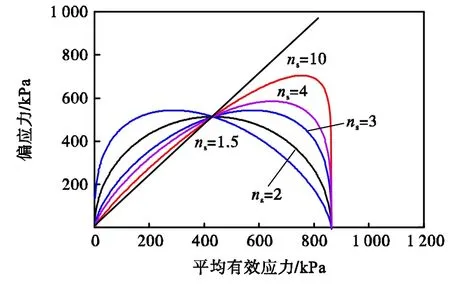
图2 扩展椭圆屈服面形状Fig.2 Shape of the extended elliptical yield surface

1.4 破损参数

鉴于室内试验无法直接获取土体破损演化规律，一般先假设后通过试验的方法间接确定，缺乏明确的物理意义.本文在岩土破损力学的框架内，结构性土颗粒可看作是由无胶结颗粒集合体和胶结颗粒集合体组成，根据均质化理论，引入体积破损率λ概念，有如下关系[26].

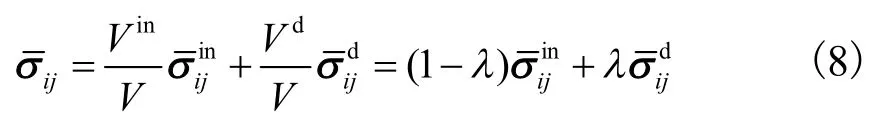
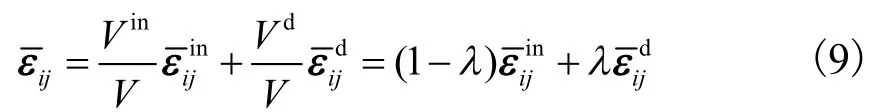
结构性土的屈服面与对应的重塑土的屈服面大小不同，但形状相似[18].如图 3所示，图中pc为重塑土屈服面在p轴上的截距.

从原点引出任意一条直线分别交重塑土和结构性土屈服面于A、B点，两点的应力状态分别可以表示为.宏观上结构性土强度组成和微观上无胶结和胶结部分应力分担之间存在以下关系[25].

在应变分担二元介质模型中有

综合式(10)、(11)可得

式中：λs为基于修正弹塑性方法定义的结构破损参数，其物理意义为代表性单元内无胶结颗粒的局部应力与代表性单元的平均应力的比值，λs会有一个初值(λs初值不能为零)，表示结构性的强弱，随着结构性土的受荷或增湿过程，会不断增加，其极限值为1，此时结构性土完全演化为重塑土.

基于宏微观土力学的研究思路，建立非饱和结构性黄土本构模型的关键为确定合理的破损参数演变规律，其需要从微观尺度对土体结构性破损演变规律进行定量分析，从而建立其与宏观力学参量间的关系.

基于二维离散元模拟结果，孙渝刚[26]选择建立大主应变与破损参数的关系，刘静德[27]选择建立等效塑性应变(包含剪切应变和体应变的复合作用)与破损参数的关系.由于结构破损参数与塑性应变的关系式中需要同时考虑塑性体应变和塑性偏应变的影响，用某种形式的等效塑性应变来描述结构破损参数演化更具有普适性.因此，本文建议将结构破损参数的演化建立在等效塑性应变之上，以上为一个关键点.对于非饱和结构性黄土而言，怎么考虑含水量变化对结构破损参数演化规律的影响是结构性黄本构模型构建的另一个关键点.

通过室内试验猜想假设[25]和非饱和结构性黄土三维离散元模拟分析可知，该离散元试样的结构破损演化速率跟含水量相关，含水量越低，结构破损速率越慢.因此，本文定义等效塑性应变与结构性土的结构屈服应力(等向压缩试验测得)的比值为等效塑性应变系数，即有为等效塑性应变.为了拓展模型的适用性，增加参数k将等效应塑形应变定义为当k＝1时，退化为.根据室内研究结构屈服应力σy′可以采用式(13)求解.

式中cy1与cy2为模型参数.

经过加荷增湿等试样离散元模拟，并分析试验过程中的土体胶结破坏过程，本文建议采用以下函数表征土体结构胶结破损规律.

令Ep＝0时的λs为其初始值λs0，则可得到cb表达式，将其代入式(14)得

式中：νs＝ca，表示结构破损演化的速率；λs0为结构破损参数初始值.

1.5 流动法则

基于修正剑桥模型剪胀率-应力关系，刘静德[27]参考 Li等[28]研究思路，建立了考虑土体状态参数ψ的剪胀率-应力关系，即

式中：Md为反映土体由剪缩到剪胀的特征状态应力比；ψ＝e-ecr为状态参数，ecr为临界状态孔隙比；n为模型参数.特别注意，虽然本文采用的剪胀率-应力关系表达式与前人相同，但是具体实施时需要采用非饱和土的有效应力比和临界状态孔隙比，比如有效应力比η′＝q/p′(式中，)考虑了非饱和土的吸力造成的黏聚力对塑性流动的影响，非饱和土的临界状态孔隙比也需要考虑吸力对临界状态压缩曲线的影响.

对剪胀率-应力关系式(16)进行积分即可得到塑性势函数.

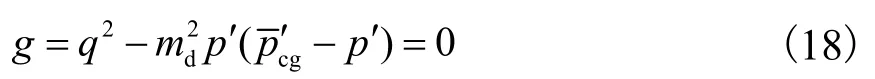
1.6 硬化规律

在修正剑桥模型中，饱和土的正常固结线(NCL)假设为直线.

式中：N为参考应力(1 kPa)对应的孔隙比；λ为土体等向压缩试验所得的压缩指数.

根据 Hu等[29]研究表明，式(21)能很好地描述非饱和土的正常固结线.

式中ah和bh为模型参数.

根据式(21)，可求出非饱和土的cp′(ξ)[30]，即

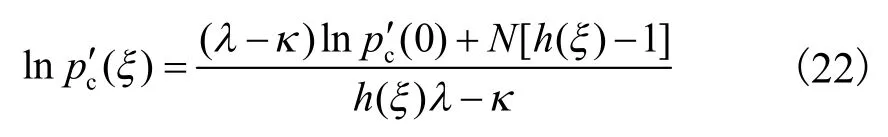
为了考虑土体状态参数ψ对硬化规律的影响，刘静德[27]在式(22)中引入了一个乘数，cp′(0)表达式改进为

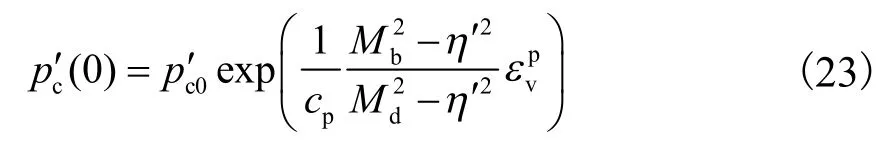
式中：Mb＝Mexp(-mψ)为土的峰值应力比[28]，m为模型参数；cp＝(λ-k)/(1+N).

式(12)、(15)、(21)～(23)联立，可得非饱和黄土的硬化规律表达式为

式中cp′即为cp′(ξ)，表达式经联立即可求得，由于较为繁琐，此处不再给出.

1.7 弹塑性矩阵

根据Hook定律，应力-应变增量关系表示为

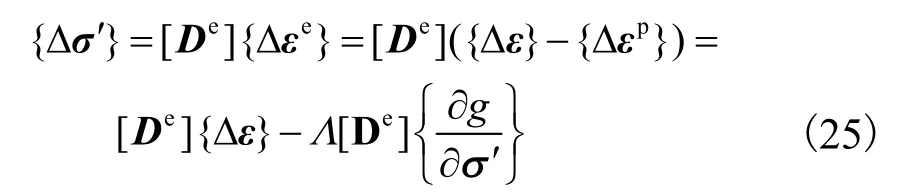
根据屈服函数f＝0，可得一致性条件为

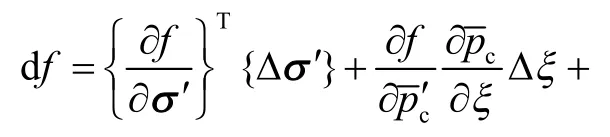
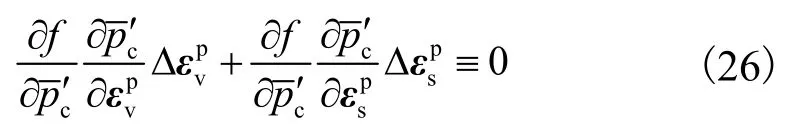
将式(26)代入式(25)，可得塑性因子，即

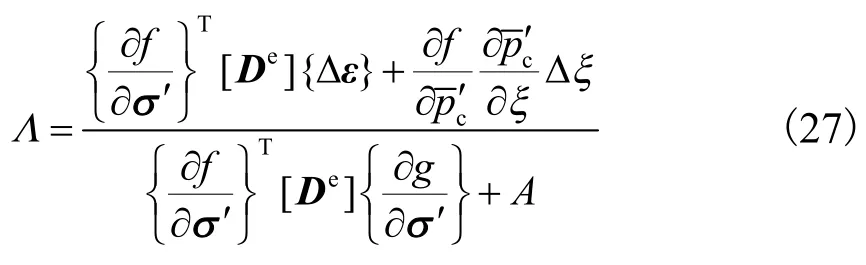
其中

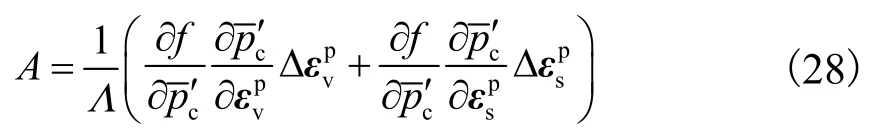
式中A为塑性硬化模量.将塑性因子带入式(25)可得

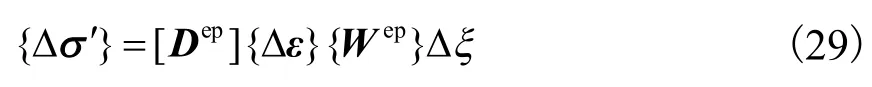
式中

2 模型参数确定

下面将模型参数分为以下几类，给出了所有模型参数的物理意义，并介绍了采用室内试验确定模型参数的方法.

(1)有效应力参数：ps0、cw、nw.

有效应力参数与土体非饱和性相关，用来计算非饱和土的吸应力，从而计算土体的有效应力，ps0一般应取为0，即饱和土的吸应力为零(黏聚力为零).

通过不同初始饱和度的重塑土等含水量三轴试验确定临界状态强度包线(p-q平面)，各状态强度包线与横轴的截距即为不同初始饱和度的吸应力，然后通过拟合获得吸应力与初始饱和度的关系获得有效应力参数ps0、cw、nw.

(2)弹性参数：κ、ν.

κ由饱和重塑土等向压缩回弹试验结果在半对数e-lnp′平面内的回弹曲线求得；泊松比ν可按经验选取.

(3)屈服面形状参数：ns.

ns可通过拟合不同应力路径下的屈服点，根据屈服点的位置确定屈服面而获得，一般建议取ns≥2，不方便确定时可以直接选定ns＝2～3.

(4)临界状态参数：Mcr、λ、N、ah、bh、m、n.

Mcr、λ、N为修正剑桥模型固有参数，ah、bh是为反映非饱和土正常固结线上移而引入的参数.

λ可由饱和重塑土等向压缩试验结果在e-lnp′平面内的压缩曲线求得；N为饱和重塑土等向压缩试验的正常固结曲线上参考应力(1kPa)所对应的孔隙比，由常规三轴试验的临界状态应力比求得，可对不同含水量试验结果取平均值.Mcr可依据不同初始饱和度重塑土等向压缩试验，ah、bh通过拟合不同饱和度(ξ＝1-Sr)在不同平均有效应力下的孔隙比比值eN/esN的关系获得.

引入参数m、n反映土体状态参数ψ对硬化规律的影响，求解ψ需知道临界状态孔隙比ecr.m、n、ecr确定方法可参见文献[27]，特别注意其主要应用于砂土，对于粉土和黏土(包括黄土)，一般取m＝n＝0.

(5)结构性参数：cy1、cy2、νs、k.

通过不同初始饱和度的结构性土等向压缩曲线可以获得结构屈服应力σy′与初始饱和度的关系，从而通过拟合获得cy1、cy2.破损参数νs可以通过试算结构性土的等向压缩线确定，参数k可通过不同应力比的等应力比压缩试验确定，也可以假设为 1，建议0≤k≤1.

3 模型验证

为验证模型的正确性及有效性，选取天然非饱和结构性黄土及人工制备结构性黄土进行模拟，并与室内试验进行对比分析.

图4给出了Q3天然非饱和结构性黄土(数据来源：文献[31]，取土地点：西安理工大学曲江校区附近)三轴试验偏应力-轴向应变关系和体应变-轴向应变关系实测结果与本文离散元模拟结果(不同初始饱和度下的等含水量(排气不排水)及相应离散元试样).采用前文提到的参数确定方法，模拟使用的参数见表1.初始饱和度Sr＝0.362编号为#1，Sr＝0.459编号为#2，三轴试验围压为 100kPa、200kPa、300kPa和 400kPa.其中，cw和nw为根据不同饱和度三轴试验临界状态强度线的横轴截距(吸应力)计算；ah和bh需要根据不同饱和度重塑土等向压缩曲线计算，本文根据不同饱和度结构性黄土压缩曲线估算.

从图 4中可以看出，由于引入了参数反映饱和度对吸应力ps和结构屈服应力σy′的影响，模型能够基本反映不同饱和度下结构性黄土在三轴试验条件下的力学特征，随着饱和度的增加，相同围压下的偏应力下降.由于结构性的影响，试样在低围压下可以表现出较高的剪切模量，试样倾向于弱硬化甚至软化，随着围压的增加试样在剪切开始就可能出现初始屈服，试样呈现硬化.

图 5给出了人工制备结构性黄土(数据来源：非饱和人工制备结构性黄土[32]的侧限压缩试验和17.7%含水量黄土等含水量三轴试验的试验结果和模拟结果.采用前文提到的参数确定方法，模拟使用的参数见表 1，试验编号为#3，三轴试验围压 5 kPa、25kPa、200kPa 和 300kPa.其中，cw、nw、ah、bh选取方法与前述一致，但因为仅有一个饱和度试验，选定nw＝1.

从图 5中可以看出，模型能够基本反映不同饱和度人工制备结构性黄土的压缩特征，对于饱和人工结构性黄土，土体在较低压力下屈服，对于 17.7%含水量结构性黄土，试样在较高压力下屈服，屈服以后试样的压缩线斜率变陡.17.7%含水量的平均有效应力较大，因此弹性模量比饱和土模拟结果大，这与试验结果相符.对于三轴试验，与天然非饱和结构性黄土试验结论相同，试样在低围压下呈现出快速到达峰值后逐步软化，在高围压下试样较早屈服后逐渐硬化，这些主要特点都能够为模型所反映.

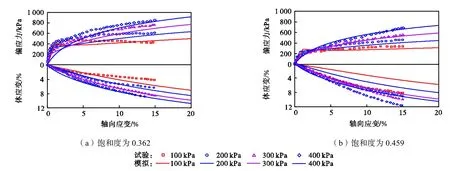
图4 非饱和结构性黄土等含水量三轴试验与模拟结果Fig.4 Predicted and experimental results in triaxial compression test on natural loess with constant water content

表1 模拟使用参数Tab.1 Model parameters used in verification tests

图5 非饱和人工制备结构性黄土侧限及17.7%含水量三轴试验与模拟结果Fig.5 Predicted and experimental results in oedometer and triaxial compression tests on artificial loess with 17.7% water content

4 结 论

本文在岩土破损力学及临界状态土力学框架内，通过胶结材料微观力学理论及三维离散元模拟分析，给出了表征结构性损伤的胶结破损规律，将其引入到硬化规律中，建立了基于经典弹塑性模型的非饱和黄土本构模型.主要得到以下结论.

(1)通过建立非饱和土吸应力与饱和度的关系得到了非饱和土有效应力表达式，可以方便地将临界状态强度线、扩展椭圆屈服面和临界状态 Lade-Duncan准则推广到非饱和土体.

(2)定义等效塑性应变系数以考虑含水量对结构破损演化参数规律的影响，胶结破损参数表达式物理意义明确，通过离散元验证分析，能够很好地反映土体结构性损伤微观机理.

(3)本文模型参数均可通过室内试验确定，Q3天然非饱和结构性黄土三轴试验及人工制备结构性黄土侧限压缩试验和三轴试验结果与本文模拟结果较为吻合，表明该模型是合理可行的.