中心锥锥角对航空发动机腔体RCS的影响

邓雪姣，李晓明，马 健，卢 婷

(中国航发四川燃气涡轮研究院，成都 610500)

1 引言

现代战争对战斗机的隐身性能提出了越来越高的要求，第五代战斗机一个最突出的特点就是低可探测技术(隐身技术)的全面应用。飞机上存在众多散射中心，进气道和航空发动机腔体就是其中重要的散射源，对发动机内部的电磁散射场进行缩减可大大降低飞行器的总体雷达散射截面(RCS)[1]。根据电磁学射线理论，对发动机内部部件外形进行优化设计可改变电磁波的传播路径，从而减小发动机前向或后向重要探测方向上的RCS。

随着计算电磁学的不断发展，形成了针对不同类型RCS 求解问题的多种计算方法，如矩量法(MOM)、多层快速多级子(MLFMM)算法、有限元法(FEM)、弹跳射线法(SBR)[2]、物理光学法(PO)、几何光学法(GO)等。其中，MOM法适用于电磁计算领域所有问题的求解，是以全波技术求解频域麦克斯韦方程组积分形式的经典算法[3]。迭代物理光学法(IPO)是在PO法的基础上考虑多次散射的一种迭代方法，用光学电流和修正电流叠加逼近导体表面的实际电流，与SBR 法相比提高了计算精度，与MOM 法相比不用对矩阵进行求逆运算，且网格划分尺度要求较低，提高了计算效率。杨涛等[4]对IPO法在航空发动机上的应用进行了研究，结果表明IPO 法具有较好的计算精度和通用性。

目前，国内对航空发动机腔体中心锥RCS 特性的相关研究较少，且主要以对部分锥角RCS的计算分析为主。如杨胜男等[5]对带中心锥航空发动机腔体电磁散射特性的数值研究。为此，本文就航空发动机腔体中心锥半锥角对RCS 的影响进行了系统的分析研究。首先采用IPO法[6-7]对带中心锥的航空发动机腔体不同半锥角模型进行RCS计算分析，然后通过MOM法进行对比验证计算，最后给出了发动机隐身设计半锥角的选择推荐值。研究结果可为发动机隐身设计提供参考。

2 计算方法

2.1 IPO法

IPO法通过对电磁波传播路径中遮挡关系的判断，以射线作为电磁波的路径进行追踪，得到腔体内部散射场[8]。图1 给出了开口腔体示意图，图中Sc为喷管壁面，Sa 为腔体的等效口径面，Es、Hs为入射电磁场，为出射电磁场。

图1 开口腔体Fig.1 Open ended cavity

IPO法的计算步骤为：

(1)根据等效定理将入射电磁波等效在Sa 面上，得到其上的等效电流[4]。

式中：na为Sa面上指向腔体内的法向单位矢量。分别代表入射磁场和电场以及Sa面上的等效磁流和电流。

(2)式(1)中求得的等效电流在腔体内壁面上产生的磁场Hc(rc)可由基尔霍夫定律近似得到[4]。

式中：rc为腔体内壁面上任意一点的位置矢量，为迭代过程中等效口径面上的中间位置矢量，为迭代过程中的等效口径面面元，j 为共轭复向量虚部单位，k为自由空间的波数，Z为自由空间的波阻抗，G为三维空间中的格林函数。

(3)由物理光学法近似得到腔体壁面上的初始电流J0(rc)[4]。

式中：nc为Sc面上指向腔体内部的法向单位矢量。

(4)通过迭代计算(迭代过程遵守遮挡关系判断)得到Sc面的电磁流解[4]。

(5)通过等效定理得到Sa面上的等效电磁流，继而求得无限远处任意点的电磁场。

2.2 MOM法

MOM法是指将算子方程化为矩阵方程，然后求解该矩阵方程的方法[3]。描述电磁场物理系统的算子方程为：

式中：x为未知等效流或场，b为激励源[9]。

用MOM法求解该算子方程的步骤如下：

(2)选择加权函数或检验函数tj，并对算子方程两边求内积得到

式(6)进一步写为

或写为矩阵形式[A][a]=[f ]。

(3)用直接法或迭代法求解矩阵方程(7)，从而获得等效流或场的未知数向量[a]。

(4)将求得的等效流带入积分方程求解任意点的电磁场。

2.3 算法验证

对单站雷达的RCS 进行计算，求解发射天线和接收天线同为水平极化或垂直极化的目标RCS，采用球面坐标系定义。入射波频率为10 GHz。

图2 IPO法、MOM法计算结果与文献结果的对比Fig.2 Comparison of IPO and MOM with reference calculation

利用IPO法和MOM法计算高12 cm、直径12 cm的圆柱腔体的单站RCS。图2给出了计算结果与参考文献[10]结果的对比，图中横坐标为水平探测方位角φ，纵坐标为探测点RCS值。由图可知，IPO法和MOM 法的计算结果与文献[10]结果基本一致，只在某些探测方位上与参考数据误差较大。图2(a)中水平极化下40°及50°探测角附近计算存在较明显的误差，图2(b)垂直极化下则误差较大。其原因在于一方面MOM法与IPO法的计算方法差异较大，另一方面不同的网格剖分形式可能造成网格面元之间遮挡关系判断的差异[11]，影响相应面元上感应电流密度的求解，从而产生一定的计算误差。

3 计算建模

以发动机后向腔体结构为基础建模。发动机后向腔体结构包含火焰稳定器、喷油杆、中心锥等多个结构。由于本文主要研究中心锥对腔体内部散射场的影响，因此省略了喷油杆和火焰稳定器等结构，并将排气机匣简化为直筒，同时将中心锥尺寸放大。发动机喷口处是涡轮、燃烧室等复杂结构，后向入射电磁波大部分被散射回去，因而喷管的进口端做短路处理为平面[12]，简化后的模型如图3 所示。腔体直径为800 mm，长度为1 000 mm，中心锥底径为540 mm，半锥角β从25°变化至65°，角度间隔为5°。对目标的单站雷达RCS 进行计算，计算频段为10 GHz，以发动机轴线为X轴，定义水平面上的探测角度为方位角φ，变化范围为-30°～30°。由于模型为轴对称形式，只计算水平面的RCS分布即可。

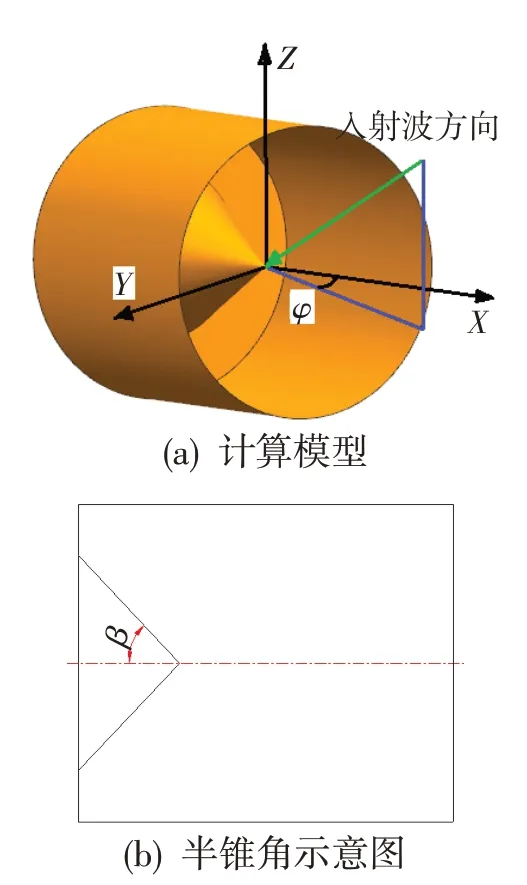
图3 带中心锥腔体计算模型Fig.3 Calculation model of cavity with central cone

4 计算结果及分析

4.1 IPO法

图4给出了IPO法计算的不同半锥角下RCS随方位角的变化。从计算结果看，RCS 随方位角变化呈中间大、两边小的对称分布，且随着方位角的增大RCS 变化更加剧烈；半锥角对0°方位角上的RCS 影响较大。0°方位角时，直射到终端面上的电磁波绝大多数按原路径反射出发动机腔体，因而回波强度最大。0°方位角附近，电磁波发生微小偏转，使得照射到终端面上的电磁波反射方向改变，回波强度急剧下降，导致RCS 大幅度减小。在0°方位角处，45°半锥角的RCS最大。

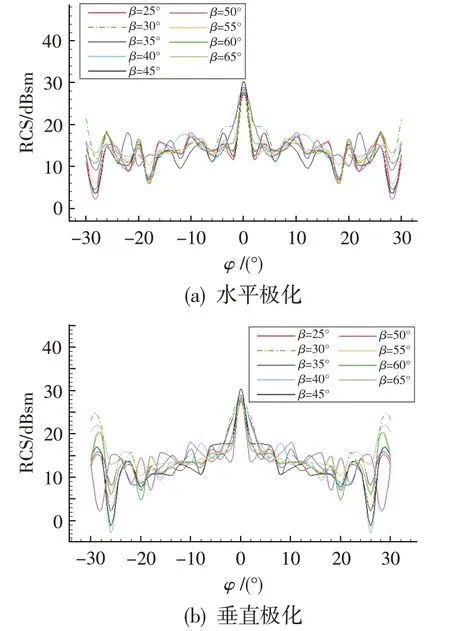
图4 不同半锥角下RCS随方位角的变化(IPO)Fig.4 Variation of RCS with detecting angle for different half cone angles(IPO)

图5 不同方位角范围内RCS均值随半锥角的变化(IPO)Fig.5 Variation of average RCS in different detecting angle ranges with half cone angle(IPO)

图5给出了不同方位角范围内RCS平均值随半锥角的变化趋势，图中RCS平均值是取不同方位角范围内各测点RCS 以m2为单位进行平均得到。从图中可看出，不同方位角范围内，45°半锥角的RCS均为最大，水平极化时30°和35°半锥角的RCS 较大，垂直极化时30°半锥角的RCS也较大。-6°～6°小方位角范围内，水平极化下30°和35°半锥角及垂直极化下30°半锥角的RCS 较大，提升了30°和35°半锥角的中心锥腔体在所有探测角度范围的RCS 均值水平。其原因是当半锥角减小到某个临界点(如30°或35°附近)后，入射到锥面上的电磁波大部分被反射到终端平面上，终端平面和直筒表面构成角反射器，将大部分电磁波散射出腔体，从概率上使得回波水平较高。在0°方位角，平行于轴线入射到45°半锥角锥面的电磁波被反射到腔体内表面后按原路径返回，因而回波强度最大，隐身设计时应避免中心锥半锥角取45°。从图中RCS 均值变化趋势看，半锥角的最佳设计值应选择在25°、40°和60°。

4.2 MOM法

图6 给出了MOM 法计算的不同半锥角下RCS随方位角的变化。与IPO 法计算的RCS 分布相似，为中间较大、两边较小的对称分布。0°方位角时45°半锥角的RCS 最大，这与IPO 法计算结果一致。相对于IPO法，MOM法计算的RCS在大方位角度范围内偏大，其原因是MOM法考虑了外部散射和边缘绕射，腔体外的圆柱表面存在法向回波[13]，使得MOM法的RCS在方位角较大时普遍大于IPO法的计算结果。

图6 不同半锥角下RCS随方位角的变化(MOM)Fig.6 Variation of RCS with detecting angle for different half cone angles(MOM)

图7 给出了MOM 法计算的不同方位角范围内RCS 平均值随半锥角的变化趋势。与IPO 法相同，均存在两个峰值点，峰值出现在30°和45°半锥角，在40°和60°半锥角附近RCS均值较低。图中显示，在40°和60°半锥角附近，RCS 在各方位角范围内均具有全局较低值，与IPO 法吻合。与IPO 法的区别在于，在25°～40°半锥角之间的RCS均值在全局都较高，造成这种现象的原因可能是由于两种计算方法原理不同所致。

图7 不同方位角范围内RCS均值随半锥角的变化(MOM)Fig.7 Variation of average RCS in different detecting angle ranges with half cone angle(MOM)

5 结论

(1)中心锥锥角对发动机腔体内部RCS 的影响规律性明显，选择合适的中心锥锥角可对腔体内部RCS产生明显的缩减效果。

(2)45°半锥角时，RCS 峰值最大，且RCS 均值在大部分方位角范围都较大，设计时需避免出现45°半锥角；在本文假定的理想模型条件下，航空发动机中心锥半锥角宜选择40°或60°。

(3)IPO 法可以较好地模拟腔体内部的散射，适用于航空发动机内部RCS 缩减设计。本文计算模型简化程度较大，在实际设计中需根据航空发动机真实结构重新考虑简化原则。

(4)半锥角存在多个选择值，中心锥的型面参数还需结合航空发动机气动性能、结构和强度等设计指标的约束进行全方位、多学科的优化设计。